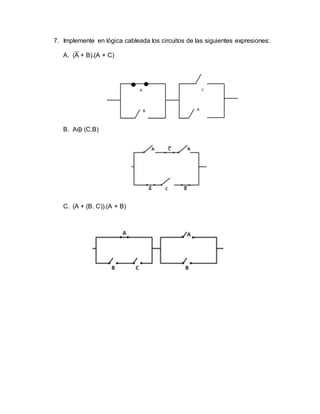
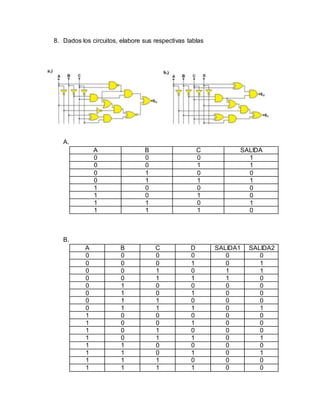
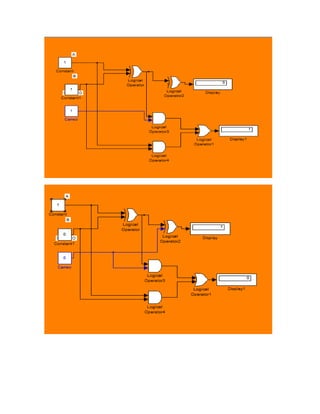
Este documento presenta un taller de matemáticas discretas realizado por tres estudiantes de la Escuela Colombiana de Carreras Industriales. El taller incluye ejercicios sobre lógica proposicional, tablas de verdad, circuitos lógicos, diagramas de Venn y estadísticas. Algunos ejercicios involucran la traducción de enunciados a su forma simbólica, la construcción de tablas de verdad y árboles, y la simplificación de expresiones lógicas.

1. ESCUELA COLOMBIANA DE CARRERAS INDUSTRIALES “ECCI”
TALLER N.1
INTEGRANTES:
CARLOS FERNANDO LEON
JORGE ALBERTO ALBARRACIN
STEVEN SERRATO GUEVARA
MATEMATICAS DISCRETAS
GRUPO 8BN
BOGOTA D.C

2. 1. Sean p = “Luis lee la prensa”, q = “Luis lee el Mundo” y r = “Luis lee el
Universal. Escriba cada una de las siguientes proposiciones en forma
simbólica.
A. Luis lee la prensa o el mundo, pero no el Universal.
( 𝑷 ∨ 𝑸) → ∼ 𝑹
B. Luis lee la prensa y el mundo, pero no lee la prensa y el universal
( 𝑷 ∧ 𝑸) → (∼ 𝑷 ∧∼ 𝑹)
C. No es cierto que Luis lee la prensa pero no el Universal.
∼ 𝑷 → 𝑹
2. Para las siguientes expresiones: construya los respectivos árboles, las
tablas de verdad y determine si son tautologías, contradicciones o
contingencias. Represente cada expresión en la notación apropiada de
Matlab.
A. [( P Q) ( P ⊻ R)] ↔ (P R) CONTINGENCIA
P Q R SOL
F F F F
F F V F
F V F V
F V V F
V F F V
V F V V
V V F F
V V V F

3. B. [( ~ ↔ R) ⟵ (P ∨ S)] ∧ (P ⊻ ∼ 𝐑) CONTIGENCIA
P R S SOL
F F F F
F F V F
F V F V
F V V V
V F F V
V F V V
V V F F
V V V F

4. C. [( P R) (P S)] ( P R) CONTIGENCIA
P R S SOL
F F F F
F F V F
F V F F
F V V F
V F F F
V F V F
V V F V
V V V V

5. 3. Para los siguientes polinomios lógicos, elabore su tabla de verdad y escriba
los polinomios en las dos formas normales disyuntiva y conjuntiva:
A. (∼ 𝑃 → 𝑄) → (𝑃 ∨ 𝑅)
P Q R SOL
F F F V
F F V V
F V F V
F V V V
V F F V
V F V F
V V F V
V V V V
𝑃 ∨∼ 𝑄 ∨ 𝑅
( 𝑃 ← 𝑄) ∨ 𝑅
B. [( P R) ( P S)] (P Q)
P Q R S SOL
F F F F V
F F F V V
F F V F F
F F V V V
F V F F V
F V F V V
F V V F V
F V V V V
V F F F V
V F F V V
V F V F V
V F V V V
V V F F V
V V F V V
V V V F V
V V V V V
𝑃 ∨ 𝑄 ∨ ~𝑅 ∨ 𝑆
𝑃 ∨ 𝑄(𝑅 → 𝑆)

6. C. [(~P ∨ R) ← (P ⊻ S)] ∧ (∼ 𝑃 ⟷ ~𝑅)
P Q S SOL
F F F V
F F V V
F V F F
F V V F
V F F F
V F V F
V V F V
V V V V
CONJUNTIVA:
(𝑃 ∨ 𝑅 ∨ 𝑆) ∧ (𝑃 ∨ 𝑅 ∨ ~𝑆) ∧ (~𝑃 ∨ ~𝑅 ∨ 𝑆) ∧ (~𝑃 ∨ ~𝑅 ∨ ~𝑆)
(𝑃 ∨ 𝑅) ∧ (𝑆 ∨ ~𝑆) ∧ (~𝑃 ∨ ~𝑅) ∧ (𝑆 ∨ ~𝑆)
( 𝑃 ∨ 𝑅) ∨ 𝑣 ∨ (~𝑃 ∨ ~𝑅) ∧ 𝑣
(𝑃 ∨ 𝑅) ∧ (~𝑃 ∨ ~𝑅)
DIYUNTIVA:
(~𝑃 ∧ 𝑅 ∧ ~𝑆) ∨ (~𝑃 ∧ 𝑅 ∧ 𝑆) ∨ (𝑃 ∧ ~𝑅 ∧ ~𝑆) ∨ (𝑃 ∧ ~𝑅 ∧ 𝑆)
(~𝑃 ∧ 𝑅) ∨ (~𝑆 ∧ 𝑆) ∨ (𝑃 ∧ ~𝑅) ∨ (~𝑆 ∧ 𝑆)
(~𝑃 ∧ 𝑅) ∨ 𝐹 ∨ ( 𝑃 ∧ ~𝑅) ∨ 𝐹
(~𝑃 ∧ 𝑅) ∨ (𝑃 ∧ ~𝑅)

7. 4. De acuerdo a las respectivas salidas determine la forma normal apropiada
(conjuntiva o disyuntiva), y reduzca el polinomio a su más mínima
expresión, mediante las reglas de reducción apropiadas y luego de ello
corrobore utilizando mapas de karnaugh
Salida 1
00 01 11 10
00 1
01 1
11 1 1
10 1 1
Factor Común:
( 𝐴̅. 𝐶. 𝐷̅) + (𝐶. 𝐴̅. 𝐵)
𝐴̅. 𝐶 (𝐷̅ + 𝐵)

8. Circuito lógico:
Salida 2:
00 01 11 10
00 1 1
01 1 1 1
11 1
10 1
Factor Común:
( 𝐶. 𝐴. 𝐵̅̅̅̅̅̅̅̅) + ( 𝐷. 𝐴. 𝐵̅̅̅̅̅̅̅̅̅) + ( 𝐷. 𝐴. 𝐵) + ( 𝐴. 𝐶̅. 𝐷) + (𝐶̅. 𝐴. 𝐵)
𝐴. 𝐵̅̅̅̅̅ + ( 𝐶. 𝐷̅̅̅̅̅) + 𝐷. 𝐴 + ( 𝐵. 𝐶̅)+ (𝐶̅. 𝐴. 𝐵)

9. 5. Simplificar las siguientes expresiones Booleanas:
A. (A + A.B +A.B.C). (A + B +C).
A. (A + B + C) + A.B (A + B + C) + A.B.C (A + B + C)
A.B + B.C + A.B +A.C + A.B.C + A.B.C + A.B.C
A (B + C + BC(C))
B. (A + B). (A + C).(B + C)
(A + B.C) (B + C)
A. (B + C) + B.C (B + C)
C. (A + B + C + A.B.C) (A + B + C)
(A + B +C) (A + B + C)
A +B +C
6. Elabore los respectivos circuitos, de manera cotidiana; con la técnica NAND
y finalmente con la técnica NOR, de las siguientes funciones:

11. 7. Implemente en lógica cableada los circuitos de las siguientes expresiones:
A. (A + B).(A + C)
B. A⨁ (C.B)
C. (A + (B. C)).(A + B)

12. 8. Dados los circuitos, elabore sus respectivas tablas
A.
A B C SALIDA
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 0
B.
A B C D SALIDA1 SALIDA2
0 0 0 0 0 0
0 0 0 1 0 1
0 0 1 0 1 1
0 0 1 1 1 0
0 1 0 0 0 0
0 1 0 1 0 0
0 1 1 0 0 0
0 1 1 1 0 1
1 0 0 0 0 0
1 0 0 1 0 0
1 0 1 0 0 0
1 0 1 1 0 1
1 1 0 0 0 0
1 1 0 1 0 1
1 1 1 0 0 0
1 1 1 1 0 0

13. 9. Utilice Simulink de Matlab para simular la correspondencia de una de las
salidas anteriores. Para garantizar la validez del ejercicio imprima un
pantallazo de la simulación.
A.
B.

14. 10.Diseñe el circuito lógico para la alarma de un automóvil, la cual detecta
cuando las luces están encendidas mientras el carro está apagado, o la
puerta del conductor está abierta, y el motor está en marcha. Los censores
están conectados a la puerta, el motor y las luces.
0 1
0 0
1 1
0 1
𝑋 = 𝐴𝐵 + 𝐴𝐶 + 𝐵𝐶̅̅̅̅
𝑋 = 𝐴𝐵𝐶̅̅̅̅̅̅ + 𝐴𝐵̅ 𝐶 + 𝐴𝐵𝐶̅ + 𝐴𝐵𝐶
A B C Salida
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1

15. 11.Elabore en Simulink el correspondiente circuito sumador completo y
verifique los resultados.

17. 12.Diseñe un circuito lógico que haga la multiplicación entre dos números: uno
de dos bits por otro de tres.

18. 13. Dados : A={a, b, c, d, f} B={a, b ,f ,g ,h ,i} C={b,c,e,g,h} D={d,e,f,g,h,i,j}
Con U= {a, b, c, d,……., z}
A. A U B:
R/: {a, b, c, d, f, g, h, i }
B. C-D:
R/: {a, k, l, m, n, o, p, q, r, s, s, t, u, v, w, x, y, z}
C. ( 𝐁 ∩ 𝐂) = ( 𝐀 ∪ 𝐁)
R/: ( 𝑩 ∩ 𝑪) = ( 𝑨 ∪ 𝑩) = { 𝟎}
( 𝑩 ∩ 𝑪) = {𝒃, 𝒈, 𝒉}
D. ( 𝑩 ∆ 𝑪 ) ∩ (𝑨 − 𝑫 )
R/: 𝑩 ∆ 𝐂 = {𝐚, 𝐟, 𝐜, 𝐨, 𝐞}
( 𝑨 − 𝑫) = {𝒌, 𝒍, 𝒎, 𝒏, 𝒐, 𝒑, 𝒒, 𝒓, 𝒔, 𝒕, 𝒖, 𝒗, 𝒘, 𝒙, 𝒚, 𝒛}
14.Mediante un sombreado adecuado en el diagrama de Venn, determine las
operaciones indicadas.
A. 𝐴 ∩ 𝐵 ∩ 𝐶
B. ( 𝐴 ∆ 𝐵) − 𝐶
C. 𝐶 ∩ (𝐴 ∪ 𝐵′
)

19. 15. Una encuesta con 100 estudiantes produjo la siguiente estadística:
 32 estudian matemáticas
 20 estudian física
 45 estudian biología
 15 estudian matemáticas y biología
 7 matemáticas y física
 10 física y biología
 30 no estudian ninguna de las 3
a) Encuentre el número de estudiantes que estudian todas las tres
e (M - e(15) – e(7) – e(10)
e((M
El número de estudiantes que gustan de las tres son: 5
b) Encuentre los respectivos números, para los estudiantes que estudian de a
dos disciplinas.
M = Matemáticas MB = 15-5 =10
F = Física MF = 7-5 =2
B = Biología MB = 10-5 =5
Los estudiantes que estudian de a dos disciplinas son 17
c) Encuentre el número de estudiantes que toman exactamente una de las tres
disciplinas
M = 32
32-(10 + 5 + 2) = 15
F = 20
20-(2 + 5 + 5) = 8
B= 45
45-(10 + 5 + 5) = 25
Los estudiantes que toman exactamente una de las dos disciplinas son
48

20. d) Llene cada una de las regiones del diagrama de Venn con los resultados del
análisis.
er
e) Elabore una estadística
Cantidad
Asignatura
Asignatura Totales Frecuencia
0 Ninguna 30 30
1 Matemáticas 15 15
Física 8 8
Biología 25 25
2
Matemáticas-Biología 10 10
Matemáticas- Física 2 2
Física- Bilogía 5 5
3
Mate-Física- Biología
5 5
Total 100 100
M B
5
F
15 25
2 5
8
10

21. 16.Establezca las operaciones de Codd indicadas para el modelo relacional de
las siguientes tablas de base de datos. Escriba el tipo de operación.
A)
SELECT e.Nombre_empleado,c.Cargo,e.Documento,c.Salario
FROM TEmpleado ec INNER JOIN TCargo c ON ec.cargo = c.Cargo,
ec.Salario = c.Salario INNER JOIN TEmpleado e ON ec.Nombre_Empleado
= e.Nombre_Empleado, ecDocumento = e.Documento
WHERE c.Salario >= 644500*2
B)
SELECT IdCargo, Cargo, Salario,SubTransporte
FROM Tcargo
WHERE Salario >1500000.
C)
SELECT *
FROM Templeados LEFT JOIN Tcargo.
D)
SELECT e.Nombre_empleado, c.Cargo, e.Documento, c.Salario
FROM TEmpleado ec INNER JOIN TCargo c ON
ec.Cargo=c.Cargo, ec.Nombre_Empleado = e.Nombre_Empleado,
ec.Documento = e.Documento
WHERE c.Salario <= 500000