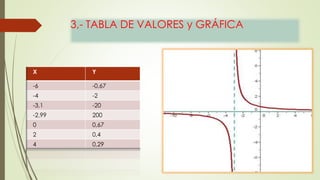
Este documento describe las funciones racionales, definidas como el cociente de dos funciones polinomiales donde el denominador no es cero. Explica que el dominio de una función racional son todos los valores reales excepto aquellos que hacen que el denominador sea cero. También muestra cómo graficar una función racional determinando primero su dominio, luego sus asintotas verticales y finalmente construyendo una tabla de valores para trazar la gráfica.

1. FUNCIONES RACIONALES
OBJETIVO:
Determinar el
comportamiento local
y global de función
racional a través del
análisis de su dominio
y gráfica.

2. DEFINICIÓN DE FUNCIÓN RACIONAL
 Una función racional es el resultado del cociente
entre dos funciones
http://mercycris.blogspot.com/
f x
( )
son funciones polinomiales, en donde
EJEMPLO:
) (x h
f (x) y gx
( )
( )
g x
h x 
g(x)  0
f (x) y gx
9
5
( )


x
h x
g(x)  0

3. DOMINIO DE FUNCIONES RACIONALES
FUNCIÓN RACIONAL PARA QUE
VALORES NO
ESTAN DEFINIDAS
LAS FUNCIONES
DOMINIO
 x  0  0 ( ) D  xR x  f x
x
x
f x
5 10
( )
2 

4. DOMINIO DE FUNCIONES RACIONALES
FUNCIÓN RACIONAL PARA QUE VALORES
NO ESTAN DEFINIDAS
LAS FUNCIONES
DOMINIO
3
x
( ) 
x 2  x

5 6
f x
5 6 2
x x
 
 x  3  x

2

 
3 0
 
2 0
 
3
 
2
x
x
x
x






x R x
  
 

2
3,
( )
x
D f x

5. GRAFICACIÓN DE FUNCIONES
RACIONALES
1.-Determino el dominio respectivo
3
2
( )


x
f x
x x
    
3 0 3
f x x R x D
( )    
3

6. 2,- Asíntotas verticales
f x 3
x   3
2
( )


x

7. 3,- TABLA DE VALORES y GRÁFICA
X Y
-6 -0,67
-4 -2
-3,1 -20
-2,99 200
0 0,67
2 0,4
4 0,29
3
2
( )


x
f x