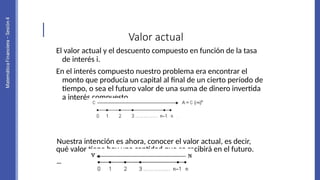
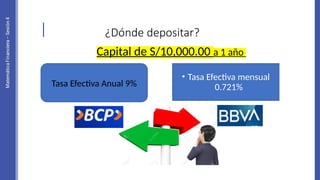
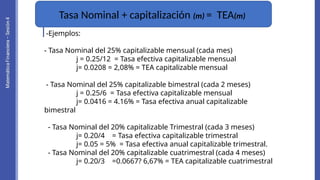
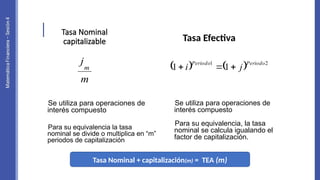
El documento aborda la capitalización de intereses y las tasas de interés nominales y efectivas, explicando cómo obtener estas tasas para diferentes períodos. Se incluyen ejemplos prácticos de cálculo de equivalencias de tasas y se discute la importancia de entender la diferencia entre tasa nominal y tasa efectiva. Además, se proponen ejercicios para aplicar los conceptos aprendidos en situaciones reales de finanzas.

1. Matemáti
ca
Sesión 4
Tema:
Capitalización de intereses y tasas de
interés Nominales y efectivas. Dada una
tasa de interés nominal hallar tasas de
interés nominales y efectivas de diferentes
plazos para un periodo de capitalización
dado.
Financiera
Programa de
Administración en
Turismo y
Hotelería

2. Resultado de
aprendizaje
Identifica el valor del dinero en el tiempo
según las teorías de la matemática financiera.
Evidencia de
aprendizaje
Estudio de Caso: Interese y tasas de
interés.

3. Contenido
Nombre del tema
• Capitalización de intereses
• Tasas de interés Nominales y efectivas.

4. Revisa el
siguiente
video:
https://www.youtube.com/watch?v=2aQd55b1sTc

5. Después de haber visualizado el video en la
slide anterior, reflexionamos y
respondemos las siguientes
interrogantes:
01 ¿Qué son las tasas de interés?
02 ¿Cuáles son las principales tasas de
interés?
03 ¿Cómo funciona el mercado respecto a las tasas de
interés?

6. Tema
Capitalización de
intereses y tasas de
interés Nominales y
efectivasdado.

7. VIDEO 4 Valor actual
https://www.youtube.com/watch?v=c_3WrejZWHQ

8. Valor actual
El valor actual y el descuento compuesto en función de la tasa
de interés i.
En el interés compuesto nuestro problema era encontrar el
monto que producía un capital al final de un cierto período de
tiempo, o sea el futuro valor de una suma de dinero invertida
a interés compuesto.
Nuestra intención es ahora, conocer el valor actual, es decir,
qué valor tiene hoy una cantidad que se recibirá en el futuro.

9. Llamamos V al valor actual y N (valor nominal) al valor futuro en la época n.
Planteando el problema dentro del campo del interés compuesto a la tasa i,
el valor actual debe ser tal que puesto a interés compuesto a la tasa i en el
tiempo n, nos dé un monto igual a N, o sea que:
Para capitalizar a interés compuesto hemos multiplicado por el factor (1 + i),
por cada año de capitalización. Para actualizar, en cambio, multiplicamos por
el factor “v” por cada período que nos retrotraemos.

10. EQUIVALENCIA DE TASAS

11. ¿Dónde depositar?
Tasa Efectiva Anual 9%
• Tasa Efectiva mensual
0.72%

12. • Dos tasas se dicen equivalentes si para un mismo
capital producen el mismo interés en un mismo
tiempo
• Dos tasas son equivalentes cuando en el mismo
horizonte de tiempo producen el mismo capital
final, pero capitalizando en períodos distintos,
siempre en forma compuesta
EQUIVALENCIA DE TASAS

13. ¿Dónde depositar?
Tasa Efectiva Anual 9%
• Tasa Efectiva mensual
0.721%
Capital de S/10,000.00 a 1 año

14. MATEMATICA FINANCIERA
TASA EFECTIVA A TASA EFECTIVA
Ejemplo 1:
Determinar la tasa equivalente del 9% efectiva anual a efectiva mensual.
Solución:
    2
1
1
1
Periodo
Periodo
j
i 


(1+0,09)^1 = (1+ j)^12
(1,09)^1/12 -1 = j
0.00721 = j
0.721% = j

15. Ejemplo 2:
Determinar la tasa equivalente del 9% efectiva anual a
efectiva bimestral.
Solución:
(1+0.09)^1 = (1+ j)^6
    2
1
1
1
Periodo
Periodo
j
i 



16. Ejemplo 3:
Determinar la tasa equivalente del 9% efectiva anual a
efectiva trimestral.
Solución:
(1+0.09)^1 = (1+ j)^4
    2
1
1
1
Periodo
Periodo
j
i 



17. Ejemplo 3:
Determinar la tasa equivalente del 9% efectiva anual a efectiva
semestral
Solución:
(1+0.09)^1 = (1+ j)^2
0.04403
4,403%
Tasa 9% efectiva o capitalizable anual = Tasa del 4,403% efectiva o
capitalizable semestral
    2
1
1
1
Periodo
Periodo
j
i 



18. Selecciona la tasa efectiva actual que paga una banco por un depósito a plazo y
determina su equivalencia en:
1.-Tasa efectiva mensual
2.-Tasa efectiva bimestral
3.-Tasa efectiva trimestral
4- Tasa efectiva semestral
5.-Tasa efectiva semanal
6.-Tasa efectiva quincenal
7.- Tasa efectiva diaria.
Casos reales

19. Se utiliza para operaciones de interés compuesto y puede dividirse o multiplicarse en “m” periodos de
capitalización.
Ejemplo:
Tasa Nominal del 25% capitalizable mensual (cada mes
j = 0.25/12
Tasa Nominal del 20% capitalizable Trimestral (cada 3 meses)
j= 0.20/4
Tasa Nominal del 20% capitalizable cuatrimestral (cada 4 meses)
j= 0.20/3
Tasa Nominal del 20% capitalizable semestral (cada 6 meses)
j= 0.20/2= 0.10
j=10%
Tasa nominal con capitalización (j)

20. Tasa Nominal capitalizable mensual del 2,083% equivale a una TNA
j = 0.02083*12 =0.25 =25%
Tasa Nominal capitalizable Trimestral del 5% equivale a una TNA
j= 0.05*4 =0.2 =20%
Tasa Nominal del 6,673% capitalizable cuatrimestral (cada 4 meses)
j= 0.0667*3 =0.20 =20%
Tasa Nominal del 10% capitalizable semestral (cada 6 meses)
j= 0.10* 2= 0.2 = 20%
Tasa nominal con capitalización (j)

21. El BCP ofrece pagar por los depósitos de sus ahorristas una Tasa
Nominal del 12% anual con capitalización bimestral (dos meses).
¿Cuál es la tasa equivalente?
j = 0.12/6
j = 0.02 =2%
Asuma un depósito de S/5,000.00 soles a un plazo de 1 año y
calcule el monto total o valor futuro que recibiría el ahorrista al
final del plazo.
Ejercicios de equivalencia de Tasa Nominal (j)

22. • SASA
Tasa Nominal + capitalización (m) = TEA(m)
Al dividir la tasa nominal jm entre el número de
capitalizaciones (m) en la unidad de tiempo, se obtiene la tasa
efectiva (TEA) en el período de capitalización .
= TEA(m)

23. -Ejemplos:
- Tasa Nominal del 25% capitalizable mensual (cada mes)
j = 0.25/12 = Tasa efectiva capitalizable mensual
j= 0.0208 = 2,08% = TEA capitalizable mensual
- Tasa Nominal del 25% capitalizable bimestral (cada 2 meses)
j = 0.25/6 = Tasa efectiva capitalizable mensual
j= 0.0416 = 4.16% = Tasa efectiva anual capitalizable
bimestral
- Tasa Nominal del 20% capitalizable Trimestral (cada 3 meses)
j= 0.20/4 = Tasa efectiva capitalizable trimestral
j= 0.05 = 5% = Tasa efectiva anual capitalizable trimestral.
- Tasa Nominal del 20% capitalizable cuatrimestral (cada 4 meses)
j= 0.20/3 =0.0667? 6,67% = TEA capitalizable cuatrimestral
Tasa Nominal + capitalización (m) = TEA(m)

24. Tasa Nominal
capitalizable
    2
1
1
1
Periodo
Periodo
j
i 


Tasa Efectiva
Se utiliza para operaciones de
interés compuesto
Para su equivalencia la tasa
nominal se divide o multiplica en “m”
periodos de capitalización
Se utiliza para operaciones de
interés compuesto
Para su equivalencia, la tasa
nominal se calcula igualando el
factor de capitalización.
Tasa Nominal + capitalización(m) = TEA (m)

25. Ejemplo 1
Asuma un ahorro de 10,000.00 y calcule el interés en un año.
    2
1
1
1
Periodo
Periodo
j
i 



26. Ejemplo 2
Una cuenta de ahorros de Caja Huancayo ofrece una TEA del
1,2% con capitalización diaria. Calcule la tasa Nominal anual
(TNA) equivalente.
Asuma un ahorro de 10,000.00 y calcule el interés en un año.
    2
1
1
1
Periodo
Periodo
j
i 


Tasa Nominal + capitalización(m) = TEA (m)

27. Ejercicios
1. Calcule la tasa efectiva semestral para un ahorro en la Caja Piura, la
cual paga una tasa nominal anual del 8% con capitalización mensual.
Asuma una capital de 5mil soles y calcule el monto total o valor
futuro en un 1 año
2.- Calcular la tasa efectiva trimestral equivalente a una tasa nominal
anual del 24% con capitalización semestral.
Asuma un capital de 8 mil soles y calcule el valor futuro en 1 año.
3.-Calcular la tasa nominal anual con capitalización mensual
equivalente a una tasa del 12% efectiva semestral.
Asuma un capital de 5 mil soles y calcule el valor futuro en 1 año.

28. Conclusiones
La tasa nominal es la tasa de interés anual sin considerar la
capitalización de los intereses. La tasa efectiva incluye la
capitalización y refleja el verdadero costo o rendimiento anual. La
tasa efectiva es siempre mayor que la tasa nominal cuando hay
capitalización más de una vez al año. Entender esta diferencia es
crucial para evaluar correctamente el costo de un préstamo o el
rendimiento de una inversión.

29. Barrera. J. A.(2021). Matemática financiera paso a paso. Alfaomega.
https://www.alphaeditorialcloud.com/reader/matematica-financiera-paso-a-paso-3?location
=1
Casusol, J. L. (2016). Modelo didáctico B-Learning para mejorar el aprendizaje de
Matemática Financiera en los estudiantes del Instituto de Educación Superior Tecnológico
Privado de Formación Bancaria Sede Chiclayo 2016. [Tesis Doctoral, Universidad César
Vallejo]. Repositorio Institucional de la Universidad César Vallejo
https://repositorio.ucv.edu.pe/handle/20.500.12692/2297
Gutiérrez, J. (2020). El Método heurístico para mejorar el Aprendizaje en matemática
financiera en estudiantes universitarios del tercer ciclo, Chepén 2019. [Tesis Doctoral,
Universidad César Vallejo]. Repositorio Institucional de la Universidad César Vallejo
https://repositorio.ucv.edu.pe/handle/20.500.12692/44926
Herrera, D. (2021). Matemática Financiera. Alfaomega.
https://www.alphaeditorialcloud.com/reader/matematica-financiera?location=1