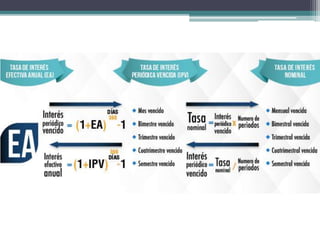
Este documento explica la diferencia entre tasas de interés nominales y efectivas. La tasa nominal solo considera el capital principal, mientras que la tasa efectiva usa la capitalización compuesta donde los intereses se suman al capital pendiente. El documento también proporciona fórmulas para calcular tasas efectivas para cualquier período e incluye ejercicios de aplicación.

1. Tasa de interés nominal y
efectiva.
Realizado por :
Ordoñez, María
27.969.775
Republica Bolivariana De Venezuela
Ministerio Del Poder Popular Para La Educación
Instituto Universitario Politécnico Santiago Mariño
Sede Barcelona

2. Introducción
• Las operaciones financieras se
realizan utilizando dos tipos de tasa
de interés, unas nominales y otras
efectivas. A su vez, éstas pueden ser
anticipadas o vencidas. Bien sea a
tasa nominal o tasa efectiva, el
presente trabajo explicara las
definiciones, características y
maneras de solucionar problemas
relacionados a tasas de interés
nominal,efectiva y equivalencias.

3. Tasa de interés nominal
• Es una tasa de referencia que
existe sólo de nombre, pues no
determina la verdadera tasa de
interés que se cobra en la
operación financiera. Esta tasa de
interés está afectada por los
periodos de capitalización de los
intereses, los cuales pueden ser:
Mensual, bimestral trimestral,
cuatrimestral, semestral.

4. Tasa de interés nominal
• La tasa de interés nominal es la
rentabilidad obtenida en una
operación financiera que se capitaliza
de forma simple, es decir, teniendo
en cuenta tan sólo el capital
principal.
• La tasa de interés nominal puede ser
diaria, semanal, trimestral, semestral
o anual.
• El TIN siempre se suele dar de forma
anualizada.

5. Tasa de interés nominal
• Su cálculo es muy sencillo, por
ejemplo, si se solicita un préstamo
de 1.000USD a una tasa nominal
del 1% mensual, los intereses
mensuales serían de 10USD. Para
conocer la tasa anual se debe
multiplicar la tasa mensual (1) por
la cantidad de meses (12), de esta
forma se obtiene una tasa nominal
anual de 12%.
Calcular

6. Tasa de interés efectiva
• En la tasa efectiva se utiliza la
capitalización compuesta, es decir,
los intereses se van sumando al
capital que está pendiente de
pagar. Es decir, la tasa efectiva es la
que se obtiene al considerar todo el
capital más los intereses que se van
generando en cada período. De esta
forma, capital más intereses se
toman como el importe total sobre
el cual se debe pagar los intereses
correspondientes al siguiente
período.

7. Tasa de interés efectiva
• La tasa de interés efectiva se
paga o se recibe por un
préstamo o un ahorro cuando
no se retiran los intereses, se
asimila a un interés compuesto.
• Esta se puede convertir en una
tasa efectiva periódica y esta, a
su vez, en una tasa nominal.
• La tasa efectiva siempre es
compuesta y vencida, ya que se
aplica cada mes al capital
existente al final del periodo.

8. Tasa de interés efectiva
• La tasa de interés efectiva se calcula
mediante la aplicación de la siguiente
fórmula.
ie= EAR= 1+ inn-1
Dónde:
• ie=EAR: es la tasa de interés efectiva
anual (la que vamos a calcular)
• i: Es la tasa de interés nominal anual (la
que el banco te ofrece)
• n: Es la cantidad de pagos consecutivos o
cuotas que cancelas en un año
Calcular

10. Tasa de interés efectiva
• La tasa de interés efectiva se calcula
mediante la aplicación de la siguiente
fórmula.
ie= EAR= 1+ inn-1
Dónde:
• ie=EAR: es la tasa de interés efectiva
anual (la que vamos a calcular)
• i: Es la tasa de interés nominal anual (la
que el banco te ofrece)
• n: Es la cantidad de pagos consecutivos o
cuotas que cancelas en un año
Para cualquier período

11. Tasa de interés efectiva
• Con la ecuación de:
𝑖 ∝= (1 + 𝑖) 𝑚 − 1
• Se calcula la tasa de interés efectiva para
un año a partir de cualquier tasa efectiva
en un periodo menor.
• Dicha ecuación se genera para
determinar la tasa de interés efectiva
para cualquier periodo.
𝑖 = (1 +
𝑦
𝑚
) 𝑚 − 1
• i efectiva para periodo
• i = Tasa efectiva para periodo
• m = Número de veces que se aplica el
interés por periodo
Para cualquier período

12. Relación Equivalente
• En los cálculos de equivalencia con
porcentajes altos, la frecuencia de
los flujos de efectivo no es igual a la
frecuencia de la capitalización de los
intereses. Resulta esencial que se
utilice el mismo periodo para el
periodo de capitalización y el
periodo de pago, y en consecuencia
la tasa de interés se ajuste.
• Cuando solo existen pagos únicos,
no hay periodo de pago PP definido
en si por flujo de efectivo ( ingreso o
egreso ). La duración del PP, por lo
tanto queda definido por periodo (t)
del enunciado de la tasa de interés
Comparación con la duración del periodo de capitalización
Periodos de pagos versus periodo de capitalización

13. Relación Equivalente
• Con solo estimaciones de P y F el
periodo de pago no se identifica de
manera específica. Es virtualmente
todas las situaciones, PP será igual a
mayor que PC. La duración del PP
se define por el periodo de interés
que se menciona en el enunciado de
la tasa de interés. Se, por ejemplo la
tasa es del 8% anual entonces PP =
PC = UN AÑO. No obstante, si la
tasa es de 10% anual con
capitalización trimestral, entonces
el PP es de 1 año, el PC es de un
trimestre o tres meses.
Pagos únicos con PP=PC

14. Relación Equivalente
• Se incluye series gradientes o
uniforme en la sucesión de flujo de
efectivo, el procedimiento es
esencialmente el mismo que el del
segundo método, salvo que ahora
PP se define para la frecuencia de
los flujos de efectivo. También
establecen la unidad de tiempo de
las tasas de interés efectivas . por
ejemplo. Si los flujos de efectivo son
trimestrales, el PP es de trimestre y
por consiguiente, se necesita una
tasa de interés efectiva trimestral. El
valor 𝑛 es el número total de
trimestre, si PP es igual a un
trimestre. Cinco años se traducen a
un valor 𝑛 de 20 trimestres. Esto
constituye una aplicación directa de
la siguiente directriz general.
Series con PP=PC

15. Ejercicios
1.¿Cuál será el monto de un capital de
$US 350, colocados al interés
compuesto del 9% anual, al cabo de 3
años? Si se supone que el interés se
capitaliza anualmente.
2.¿Un cliente pregunta a su banquero,
en que suma se convertirá su depósito
de $ 6.000, colocados durante 9 años al
interés compuesto del 14% capitalizable
anualmente?

16. Ejercicios
3.El señor Mario Oropeza, depositó $US
1.200, en el Banco Norte que paga el 14%
capitalizable anualmente. ¿Cuántos años
deberá transcurrir para poder obtener un
monto de $US 1.459,98?
4.¿A qué tasa o tipo de interés fueron
colocados $US 2.500, en el Banco
Internacional, si al cabo de 10 años
devolvieron $US 3.700, considerando interés
compuesto y capitalización anual?

17. Ejercicios
5. El banco Bisco, paga a sus depositantes el
14 ½% compuesto capitalizable
semestralmente. ¿Si se deja un depósito de $
500, durante 1 año que cantidad obtendrá?
6.La Señora Nilda López, coloca $ 12.000, al
15% de interés compuesto semestral por el
lapso de 1.5 años capitalizables
trimestralmente. Se pide calcular el capital
final o monto a interés compuesto.

18. En conclusión la tasa nominal y efectiva tienen la misma relación que
entre sí guardan el interés simple y el compuesto. La diferencia es que
las tasas de interés efectivas se utilizan cuando el periodo de
capitalización (o periodo de interés), es menor a un año. Dentro del
mundo de las Finanzas existen diversas herramientas que ayudan a
empresas e individuos a tomar las decisiones de inversión que les
garanticen beneficios en el futuro, todas las empresas se enfrentan a
estas decisiones diariamente, Por lo que es importante realizar todas
las operaciones de manera correcta.

19. • https://www.coltefinanciera.com.co/educacion-financiera/tasas-y-tarifas/425-cual-es-la-tasa-interes-
nominal-y-efectiva
• https://enciclopediaeconomica.com/tasa-de-interes/
• https://definicion.de › tasa-efectiva
• https://www.academia.edu/27586202/TASAS_NOMINALES_Y_EFECTIVAS_DE_INTER%C3%89S
• http://matefinan-der.blogspot.com/2010/11/tema-5-los-periodos-de-capitalizacion.html
•