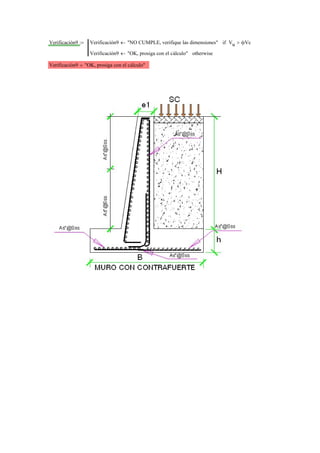
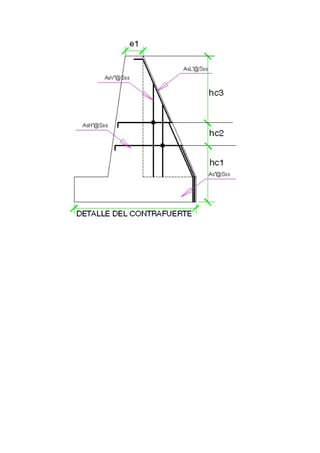
Este documento presenta el diseño de un muro de contención con contrafuertes. En 3 oraciones:
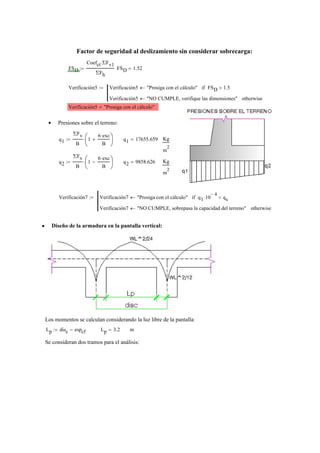
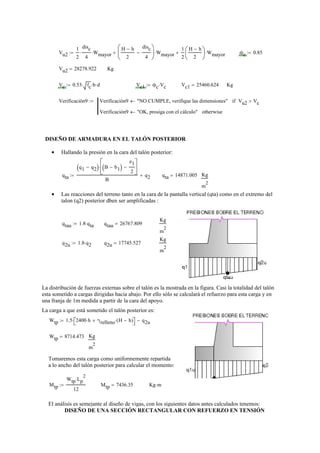
1) Se realiza el cálculo de la estabilidad del muro considerando fuerzas como el empuje del terreno y sobrecargas, y se verifica que cumple con factores de seguridad contra volteo y deslizamiento.
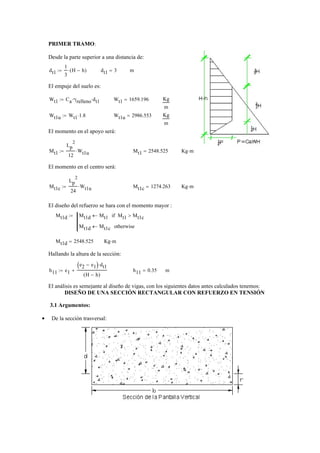
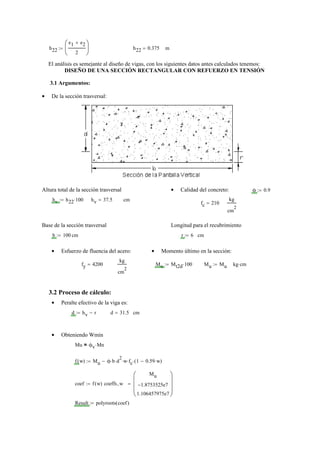
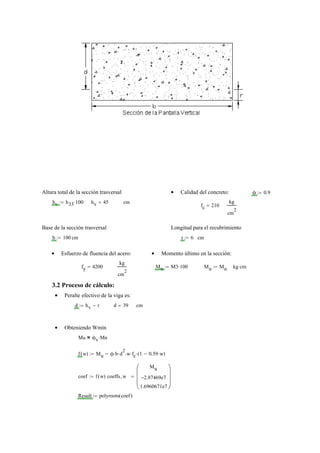
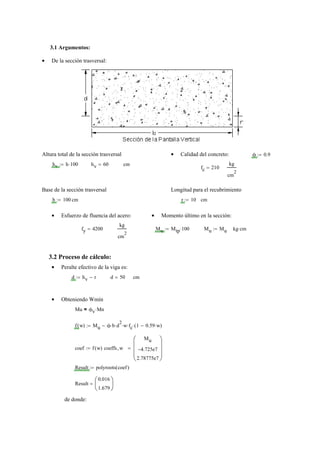
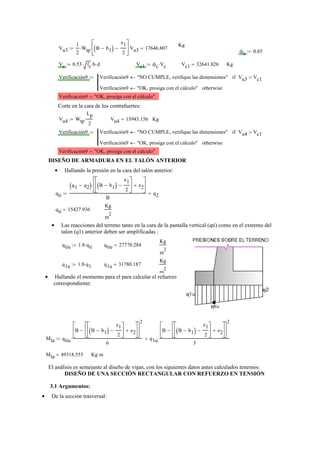
2) Luego, se dimensiona la sección transversal de la pantalla de contención, calculando momentos y diseñando la armadura para resistirlos.
3) Finalmente, se verifica que la cantidad de acero dise