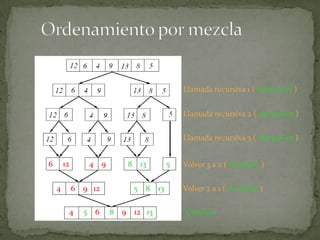
El algoritmo de ordenamiento por mezcla (mergesort) se basa en la técnica divide y vencerás. Divide la secuencia a ordenar en subsecuencias más pequeñas de manera recursiva, ordena las subsecuencias de forma independiente y luego las combina para obtener la secuencia ordenada final. Tiene una complejidad de O(n log n) y es un método estable, aunque requiere más espacio de memoria que otros algoritmos como heapsort.

1. MergesortJulio Cesar García Lechuga 1449675 Raúl Rodríguez Salazar 1460392Alberto Huerta Jaramillo

2. Se basa en la técnica divide y vencerás (DYV).Divide: Divide la secuencia de n elementos en dos subsecuencias de n/2 elementos.Vence: Ordena ambas subsecuencias de manera recursiva.Ordenamiento por mezcla

3. Combina: Mezcla las dos subsecuencias ordenadas para obtener la solución del problema.

4. Si A[n..] (n==1){«Esta Ordenado»}Si noRealiza {A[n]/2;}Mientras (n=!1)MezclaPseudocódigo

5. Ordenamiento por mezcla Llamada recursiva 1 ( MergeSort) Llamada recursiva 2 ( MergeSort) Llamada recursiva 3 ( MergeSort)6 12 4 9 8 13 5 Volver 3 a 2 ( Combina )4 6 9 12 5 8 13 Volver 2 a 1 ( Combina ) 4 56 89 12 13Combina

6. 1. Si la longitud de la lista es 0 ó 1, entonces ya está ordenada. En otro caso:2. Dividir la lista desordenada en dos sublistas de aproximadamente la mitad del tamaño.Funcionamiento

7. 3. Ordenar cada sublista recursivamente aplicando el ordenamiento por mezcla. 4. Mezclar las dos sublistas en una sola lista ordenada.Funcionamiento

8. Ejemplo de ordenamiento por mezcla ordenar una lista de puntos aleatorios.

9. Método estable de ordenamiento mientras la operación de mezcla (Merge) sea bien implementada.Este algoritmo es efectivo para conjuntos de datos que se puedan acceder secuencialmente como arreglos, vectores y listas ligadasVentajas

10. Su principal desventaja radica en que está definido recursivamente y su implementación no recursiva emplea una pila, por lo que requiere un espacio adicional de memoria para almacenarla.Desventajas

11. El ordenamiento por mezcla tiene una complejidad de O(n logn).Complejidad

12. Aunque heapsort tiene los mismos límites de tiempo que merge sort, requiere sólo O(1) espacio auxiliar en lugar del O(n) de merge sort, y es a menudo más rápido en implementaciones prácticas.Comparación con otros algoritmos de ordenamiento

13. Quicksort, sin embargo, es considerado por mucho como el más rápido algoritmo de ordenamiento. Mergesort es un ordenamiento estable, paraleliza mejor, y es más eficiente manejando medios secuenciales de acceso lento.Comparación con otros algoritmos de ordenamiento

14. Merge sort es a menudo la mejor opción para ordenar una lista enlazada: es relativamente fácil implementar merge sort de manera que sólo requiera Θ(1) espacio extra.Comparación con otros algoritmos de ordenamiento

15. http://es.wikipedia.org/wiki/Ordenamiento_por_mezclawww.dtic.upf.edu/~jonsson/pII09/Apuntes/TeoriaSemana5.ppthttp://aprende-sistemasarreglos.blogspot.com/2009/03/mergesort.htmlReferencia Bibliográfica