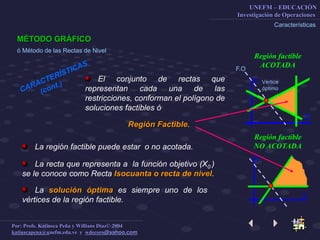
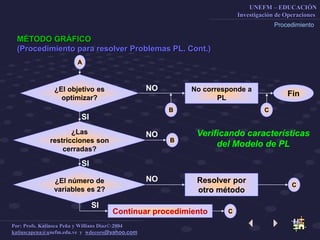
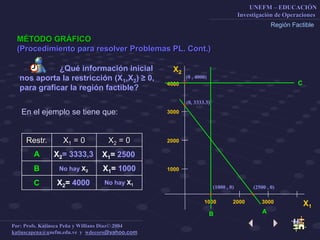
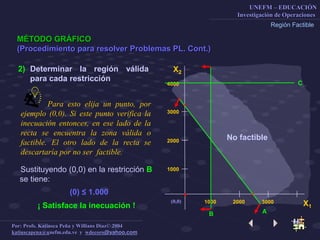
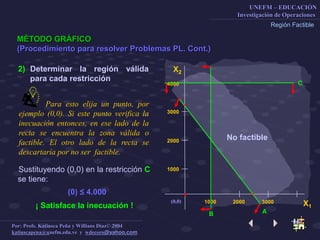
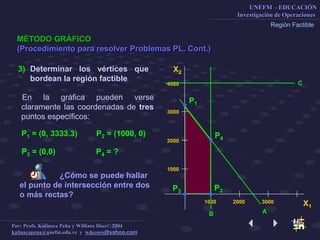
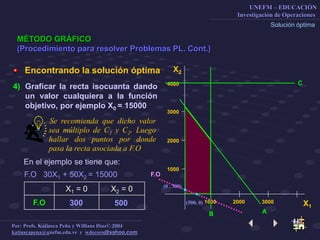
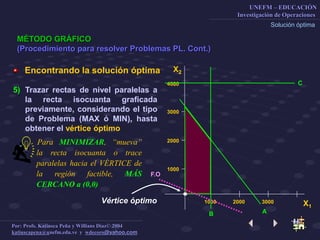
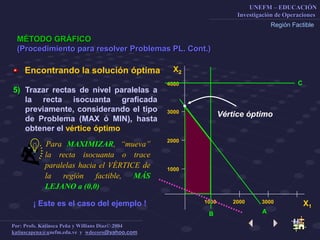
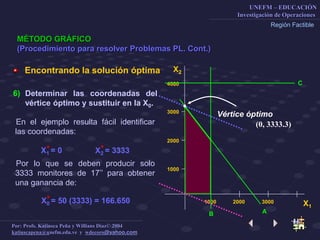
Este documento describe el método gráfico para resolver problemas de optimización restringida mediante el uso de rectas de nivel. Explica el procedimiento paso a paso, que incluye determinar la región factible, graficar la función objetivo, y encontrar el vértice óptimo para maximizar la función. El objetivo es enseñar a los estudiantes a resolver problemas de optimización restringida usando este método gráfico.