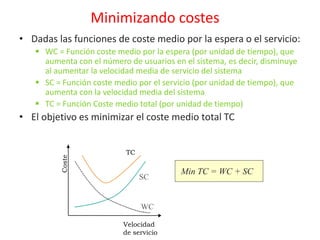
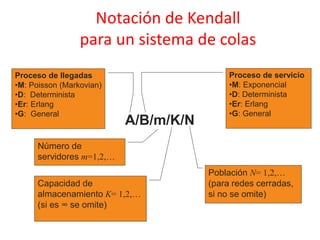
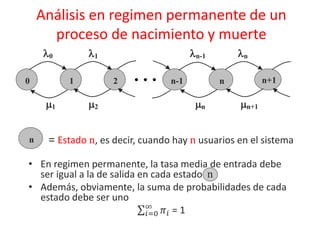
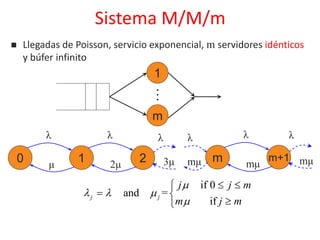
El documento presenta conceptos básicos sobre modelado de redes, incluyendo multiplexación estadística, colas, probabilidad de overflow y ancho de banda efectivo. También introduce la teoría de colas, parámetros como intensidad de tráfico y factor de utilización, y la notación de Kendall para sistemas de colas. Finalmente, explica las propiedades de la distribución exponencial y su relación con los procesos de Poisson, elementos clave para la modelización de sistemas de colas.

1. Carlos López Ardao
Escola Enxeñería Telecomunicación
Universidade de Vigo
Tema 1: Modelado de redes (I)
Tecnoloxías de Rede

2. Tema 1: Modelado de redes (I)
Enlaces: Multiplexación estadística
y colas

3. Multiplexación estadística
• Múltiples fuentes de tráfico (tasa pico R bps y
tasa media λ bps) comparten el mismo enlace
 Para garantizar que no hay pérdidas y que los retardos
son bajos, podemos asignar BW= 𝑅  A costa de
gran infrautilización de recursos
 Lo habitual es asignar un BW ligeramente superior a
λ ya que la probabilidad de que el tráfico agregado
supere la suma de tasas medias es pequeña 
Multiplexación estadística  Colas y pérdidas
Contienda por BW  ColaNo contienda por BW  No cola

4. Ejemplo
• Enlace de C=10 Mbps compartido por múltiples fuentes:
 Probabilidad fuente activa p = 0.1
 R = 100 kbps  λ = p.R = 10 kbps
• Asignación según tasa de pico  N = C/R = 100 fuentes
• Pr( 𝑖=1
𝑛
𝑋𝑖 ≥ 100) es la probabilidad de que la tasa
agregada exceda la capacidad del enlace. Aplicando el
límite de Chernoff para v.a. Bernoulli

5. Pérdidas
• Hemos visto que la multiplexación estadística
funciona bien incluso sin búfer
• En la práctica, cuando el número de llegadas
excede la capacidad del enlace, los paquetes son
almacenados en un búfer, en espera de ser
transmitidos (cola), en lugar de ser descartados
• Estudiaremos la probabilidad de que el número
de paquetes almacenados en un búfer infinito
exceda cierto umbral B

6. Probabilidad de overflow y ancho de
banda efectivo
• N fuentes de tráfico (tasa pico R bps y tasa media λ bps) comparten
el mismo enlace de capacidad C bps. λ < C/N
• Teorema: ∀𝜃 > 0/
𝐴(𝜃)
𝜃
< C/N
Pr 𝑄 ≥ 𝐵 ≤
𝑒 𝑛𝐴 𝜃 −𝜃𝐶
1−𝑒 𝑛𝐴 𝜃 −𝜃𝐶 𝑒−𝜃𝐵
• Se trata de un límite superior que sirve para observar que la
probabilidad de overflow decrece exponencialmente con B con tasa
de caída 𝜃
• La cantidad
𝐴(𝜃)
𝜃
se denomina ancho de banda efectivo (Bwef) de
una fuente
 Para 𝜃 → 0  BWef → λ
 Para 𝜃 → ∞  BWef → R
 𝜃 es así una medida del nivel de exigencia de los requisitos QoS.
Cuanto mayor es 𝜃, mayores son los requisitos QoS

7. Tema 1: Modelado de redes (I)
Análisis de retardos y
pérdidas en colas

8. Teoría de colas
• Especificación de un Sistema de colas:
 Proceso de llegadas: Flujos, sesiones, paquetes, etc.
Caracterizado por el proceso de tiempo entre llegadas A. Si
denominamos λ a la tasa media (en llegadas/sg.)
o E(A) = 1/ λ
 Distribución S del tiempo de servicio o, alternativamente,
distribución de la longitud del mensaje, sesión, tamaño del
flujo, etc. para un enlace de capacidad C bps. Si denominamos
µ a la velocidad media de servicio (en unidades/sg.)
o E(S) = 1/µ
 Tamaño del búfer
 Número de servidores m (líneas de salida, enlaces) de idéntica
capacidad
 Disciplina de la cola: FCFS, SJF, PQ, RR

9. Parámetros de un Sistema de colas
• Orientadas al sistema:
 Intensidad de tráfico ofrecido I
 Intensidad de tráfico cursado IC (sistemas con bloqueo o
rechazo)
• Factor de utilización o ocupación (ρ) de un recurso
• Orientadas al usuario:
 En sistema de espera:
o El número medio de usuarios en el sistema (𝑁) y en la cola (𝑄)
o El tiempo medio de estancia en el sistema (𝑇) y en la cola (𝑊)
 En sistemas con bloqueo o rechazo:
o Probabilidad de bloqueo B  IC = I.(1-B)

10. Ley de Little
 a(t): proceso que cuenta el número de llegadas hasta t
 d(t): proceso que cuenta el número de salidas hasta t
 γ(t): Tiempo total en el sistema invertido por los usuarios (hasta t)
 N(t)= a(t)- d(t)
N(t)
a(t)
Time t
Area γ(t)
 Tasa media de llegadas (hasta t)  λ(t)= a(t)/t
 Tiempo medio que pasa un cliente en el sistema (hasta t)  T(t)= γ(t)/a(t)
 Número medio de usuarios en el sistema (hasta t)  N(t)= γ(t)/t
d(t)Tiempo en el sistema
invertido por usuario 1

11. Ley de Little
 Despejando γ(t) en ambas tenemos: T(t).a(t) = N(t).t
 Y de ahí  N(t) = λ(t).T(t)
 Tomando el límite cuando t tiende a infinito
𝑁 = λ.𝑇
Número medio de
clientes en el sistema
Tiempo medio de estancia
en el sistema
Tasa media de llegadas
N(t)
a(t)
Time t
Area γ(t)
d(t)

12. Generalidad de la Ley de Little
𝑁 = λ.𝑇
 La ley de Little es un resultado bastante general
 No depende del proceso de llegadas
 No depende de la distribución de servicio
 No depende del número de servidores ni del búfer
 Es aplicable a cualquier subsistema
• Si nos centramos sólo en la cola tenemos
𝑄 = λ.𝑊
• Si nos centramos sólo en los servidores tenemos
I = λ.𝑆 = λ/μ
• Y dado que 𝑇 = 𝑊 + 𝑆 tras multilpicar por λ se sigue que
𝑁 = 𝑄 + I

13. Intensidad de tráfico
• Intensidad de tráfico ofrecido I es el número medio de recursos
ocupados en un sistema de referencia con capacidad infinita e
infinitos recursos idénticos al real. Según la Ley de Little, I=/
 Para que un sistema esté bien dimensionado  I < m
• Intensidad de tráfico cursado IC es el número medio de recursos
ocupados
 Coincide con I en un sistema sin rechazos ni bloqueos
 En un sistema con probabilidad de bloqueo B, si c =(1-B) es la tasa
media cursada o caudal de salida (throughput) tendremos que
Ic= c/ = (1-B)/ = I(1-B)
• Factor de utilización u ocupación (ρ) de un recurso es la probabilidad
de que dicho recurso esté ocupado y, por tanto, equivale al tráfico
medio cursado por dicho recurso. Así, aplicando la fórmula de Little a
un único recurso, tenemos
𝜌 =
𝐼𝑐
𝑚
=
𝜆 𝑐
𝑚𝜇

14. Notación de Kendall
para un sistema de colas
A/B/m/K/N
Proceso de llegadas
•M: Poisson (Markovian)
•D: Determinista
•Er: Erlang
•G: General
Proceso de servicio
•M: Exponencial
•D: Determinista
•Er: Erlang
•G: General
Número de
servidores m=1,2,…
Capacidad de
almacenamiento K= 1,2,…
(si es ∞ se omite)
Población N= 1,2,…
(para redes cerradas,
si no se omite)

15. • Los modelos de colas mas comunmente usados se basan en
la suposición de tiempos de servicio y tiempos entre
llegadas distribuidos exponencialmente
Definición: Una v.a. Texp( ) está distribuida
exponencialmente con parámetro , si su función de
densidad de probabilidad es:
La distribución exponencial







0twhen0
0twhene
)t(f
t
T
t
T e1)t(F 
 Su función de distribución es:
 La media es E[T] = 1/
 La Varianza es Var[T] = 1/ 2

16. La distribución exponencial
Tiempo entre llegadas
Media =
E[T]=1/
Densidaddeprobabilidad
t
fT(t)

t
e 
 

17.  Propiedad 1: fT(t) es estrictamente decreciente en t
 P(0Tt) > P(t T t+t) para todo t, t0
 Implicaciones
 Muchas realizaciones de T (es decir, valores de t) serán pequeños; entre cero y la
media
 No es adecuado para describir tiempos de servicio cuando éstos deberían
hallarse centrados en torno a la media
 En cambio, es razonablemente adecuado en aquellas situaciones en las que
diferentes clientes requieren diferentes tipos de servicio
 También es a menudo una descripción razonable del tiempo entre llegadas de
usuarios, fundamentalmente cuando se trata de personas independientes que
deciden hacer algo (llamar por teléfono, iniciar una sesión Web, ir al cine,etc.). En
el caso de tráfico de datos es una aproximación más aceptable a medida que se
aumenta la escala temporal
Propiedades de la distribución exponencial

18.  Propiedad 2: Sin memoria
 P(T>t+t | T>t) = P(T >t) para todo t, t0
 Implicaciones
– No importa cuando llegó el ultimo cliente (o cuanto tiempo de
servicio haya demandado el ultimo usuario), la distribución del
tiempo hasta la siguiente llegada (o del siguiente tiempo de
servicio) es siempre la misma
– Es usualmente una suposición razonable para tiempos entre
llegadas
– Para tiempos de servicio puede ser más cuestionable. Sin
embargo, una vez más es razonablemente adecuado en aquellas
situaciones en las que diferentes clientes requieren diferentes
tipos de servicio
Propiedades de la distribución exponencial (II)

19.  Propiedad 3: El mínimo de un conjunto de v.a.
independientes exponencialmente distribuidas posee
también distribución exponencial
 Implicaciones
– Las llegadas procedentes de n fuentes independientes con tiempos
entre llegadas exponencialmente distribuidos y tasas {1, 2, …, n}
pueden ser tratadas como un único proceso homogéneo con
tiempos entre llegadas exponencialmente distribuidos y tasa
= 1+ 2+…+ n
– Un conjunto de n servidores en paralelo con tiempos de servicio
exponencialmente distribuidos y tasas de servicio {1, 2, …, n}
puede ser tratado como un único servidor con tiempos de servicio
exponencialmente distribuidos y tasa = 1+2+…+n
Propiedades de la distribución exponencial (III)

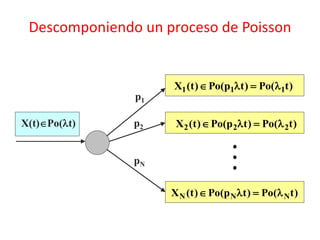
20.  Relación con el proceso de Poisson
Sea X(t) el número de eventos que ocurren en el intervalo [0,t]. Si
el tiempo entre eventos consecutivos es T and Texp()
 X(t)Po(t)  {X(t), t0} es un proceso de Poisson
Propiedades de la distribución exponencial (IV)
...,1,0nfor
!n
e)t(
)n)t(X(P
ntn





21.  La suposición habitual en muchos modelos de
colas es que el proceso de llegadas es de Poisson
• Dos definiciones equivalentes del proceso de
Poisson
1. Los tiempos entre llegadas son variables
aleatorias i.i.d. con distribución exponencial de
media 1/ 
2. X(t) es un proceso de Poisson con tasa de
llegadas 
El proceso de Poisson

22.  Los procesos de Poisson pueden agregarse o
desagregarse y los procesos resultantes son también de
Poisson
a) La agregación of N procesos de Poisson con tasas
{1, 2, …, n} es un nuevo proceso de Poisson con
tasa = 1+ 2+…+ n
b)Descomponer un proceso de Poisson X(t)Po(t)
en N subprocesos {X1(t), X2(t), , …, XN(t)} (por
ejemplo N tipos de clientes) donde Xi(t)Po(it)
puede hacerse si
•Para cada llegada, la probabilidad de pertenecer
al subproceso i es pi
• p1+ p2+…+ pN = 1, y i =  .pi
Propiedades del proceso de Poisson

23. Descomponiendo un proceso de Poisson
X(t)Po(t)
)t(Po)tp(Po)t(X 111 
)t(Po)tp(Po)t(X 222 
)t(Po)tp(Po)t(X NNN 
p1
p2
pN 

24. La propiedad PASTA (Poisson Arrivals See Time Averages)
 Sea πj(t)= Pr{X(t)= j} la probabilidad de que el estado del sistema sea j
(haya j usuarios) en el instante t
 Sea aj(t)= Pr{Un cliente que llega al sistema se encuentre X(t)= j
usuarios}
 En general πj(t) ≠ aj(t)!
 Supongamos un sistema D/D/1 con tiempos entre llegadas igual a 1 y
tiempos de servicio igual a 0.5
0 0.5 1.0 1.5 2.0 2.5 3.0
a a a a
 En este ejemplo puede verse que π0(t)=0.5 y π1(t)=0.5 mientras a0(t)= 1 y
a1(t)= 0!
 Para un sistema de colas, cuando el proceso de llegadas es de Poisson y es
independiente del proceso de servicio, la probabilidad de que un cliente que llega
al sistema se encuentre j clientes en el sistema es igual a la probabilidad de que e
sistema se halle en el estado j. En otras palabras,
      Pr , 0,1,...j ja X j jt t t   

25.  Es la base de muchos de los modelos de colas más
habitualmente usados
 Nacimiento – equivale a la llegada de un usuario
 Muerte – equivale a la salida de un usuario servido
Suposiciones
1. Dado N(t)=n,
 El tiempo entre nacimientos (TN) es distribuido exponencialmente con
parámetro n (los clientes llegan según un proceso de Poisson)
 El tiempo de servicio demandado (TM) es distribuido exponencialmente
con parámetro n
2. TN & TM son v.a. independientes y en cada instante sólo puede
ocurrir exactamente un Nacimiento (n  n+1) o una Muerte (n
 n–1)
Procesos de nacimiento y muerte

26. Análisis en regimen permanente de un
proceso de nacimiento y muerte
0 1 n-1 n
0 1 2 n-1 n n+1
1 2 n n+1
n = Estado n, es decir, cuando hay n usuarios en el sistema
• En regimen permanente, la tasa media de entrada debe
ser igual a la de salida en cada estado n
• Además, obviamente, la suma de probabilidades de cada
estado debe ser uno
𝑖=0
∞
𝜋𝑖 = 1

27. Ecuaciones de un proceso B-D
 En régimen permanente, obtenemos
λ0
0 1μ1
λ1
2μ2
λj-2
j-1μj-1
λj-1
jμj
μ3
λ2
λj
μj+1
0 0 1 1 0    
0
1 0
1

 

 
 En general
 1 1 1 1 0j jj j j j j
        
  
0
1 0
1 1
...
...
j
j
j
 
 
 

 
    
 
 Haciendo la suma igual a 1
0 1
0
1 1
...
1 1
...
j
j j
 

 



  
     
  

Existe solución si
0 1
1 1
...
1
...
j
j j
S
 
 



 
     
 


28. Sistema M/M/1
 Llegadas de Poisson, servicio exponencial, un servidor único y
búfer infinito
λ
0 1μ
λ
2μ
λ
j-1μ
λ
jμμ
λ λ
μ
 Usando las expresiones de un proceso B-D con λj=λ y μj=μ
(λ < μ), obtenemos
0 , 0,1,2,...
j
j j

 

 
  
  Haciendo =λ/μ
0 1  
  , 1,2,...1 j
j j  
Pr 𝑛 ≥ 𝑘 =
𝑗=𝑘
∞
𝜋𝑗 = 𝜌 𝑘
𝜋0 = 1 +
𝑗=1
∞
 𝑗
−1
= 1 +

1 − 
−1
= 1 − 
Cota superior al bloqueo en M/M/1/K

29. Sistema M/M/1 (cont.)
 Número medio de usuarios
     
 
0 0 0
1 1
j
j
j
j j j
d
E j jX
d

   

  
  
      
   
   0
1
1 1
1 1
j
j
d d
d d

   
   


    
      
     

𝑁
 Tiempo medio de estancia
𝑁 = 𝜆. 𝑇 ⇒ 𝑇 =
𝑁
𝜆
=
𝜌
𝜆(1−𝜌)
=
1
𝜇(1−𝜌)
 Tiempo medio de espera en cola
𝑊 = 𝑇 − 𝑆 =
1
𝜇 1 − 𝜌
−
1
𝜇
=
𝜌
𝜇 1 − 𝜌
 Tamaño medio de la cola
𝑄 = 𝜆. 𝑊 =
𝜆. 𝜌
𝜇 1 − 𝜌
=
𝜌2
1 − 𝜌

30. Ejemplo de prestaciones M/M/1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
5
10
15
20
25
30
35
40
rho
Delay(timeunits)/Numberofcustomers
μ=0.5
𝑁
𝑊
𝑇

31. Sistema M/M/m
λ
0 1μ
λ
22μ
λ
mmμ
λ
m+1
mμ3μ
λ λ
mμ
1
m
…
if 0
and =
if
j j
j j m
m j m

  

 
 

 Llegadas de Poisson, servicio exponencial, m servidores idénticos
y búfer infinito

32. Ssistema M/M/m
0
1
, if
!
j
j j m
j

 

 
  
 
 Haciendo ρ=λ/(mμ) obtenemos
0 , if
!
jm
j
m
j m
mm

 

 
  
 
 
0
0
if
!
if
!
j
j
m j
m
j m
j
m
j m
m








 


 1
0
1
11
! !
j m jm
j j m
m m
j m
 

 
 
 
   
 
 
   
 
1
1
0
1
1
! ! 1
j mm
j
m m
j m
 





 
      

 Para hallar π0
 Usando las expresiones generales de un proceso B-D, obtenemos

33.  
 1
0
0 1
...
! !
j mm
j
j
j j j m
m m
E j j jX
j m

  
  
  
 
    
 
  
 
 
 
02
! 1
m
m
E mX
m
 
 

 

 Usando la Ley de Little
   
 
 
02
1 1
! 1
m
m
E E mS X
m
 
 
  
 
   
  
    1E EW S  
𝑁
𝑁
𝑁𝑇
𝑊 𝑇
 Número medio de usuarios
Sistema M/M/m (cont.)
 Función de probabilidad (Expresión Erlang-C)
Pr 𝑛 ≥ 𝑘 =
𝑗=𝑘
∞
𝜋𝑗 = 𝜋0
𝑗=𝑘
∞ 𝑘 𝑘 𝜌 𝑗
𝑘!
=
𝜋0(𝑘𝜌) 𝑘
𝑘! (1 − 𝜌)
𝑃𝑄 = Pr 𝑛 ≥ 𝑚 =
𝜋0(𝑚𝜌) 𝑚
𝑚! (1 − 𝜌)
Muy usada para call centers

34. Ejemplo
 Los clientes llegan según un proceso de Poisson de tasa λ=1. Se
nos ofrecen las dos siguientes opciones:
 A) Instalar un servidor único con capacidad de procesado μ1= 1.5
 B) Instalar dos servidores idénticos con capacidades de procesado μ2=
0.75 y μ3= 0.75 y cola única
 C) Repartir de forma equiprobable el tráfico entrante a dos colas
atendidas por sendos servidores idénticos con capacidades de procesado
μ2= 0.75 y μ3= 0.75
μ1
λ
Α
μ2
μ3
λ
Β
μ2
μ3
λ
C
λ/2
λ/2

35. Ejemplo
• IA = λ/μ1 = ρA = 2/3
• IB = λ/μ2 = 4/3  ρB = IB/2 = 2/3
• Ic = 0’5.λ/μ2 = ρC = 2/3
0
1
1
1
3
A



  
Para cada servidor0
2
1
1
2 3
C



  
12
4
14 31
523
2 1
3

  
  
    
  
  
  
   
 
1
1
0
1
1
! ! 1
j mm
j
m m
j m
 






 
     


36. Ejemplo
 Tamaño de cola y retardos
 
1
1
2
1.5 1
AE X

 
  
 
Cada cola en C es independiente!. Si lo vemos de forma conjunta,
tenemos igualmente que 𝑇𝑐 =
2.𝑁1𝐶
𝜆
= 4
 
 
 
02
12
! 51
m
B
m
E mX
m
 
 

  

 1
2
/ 2 0.5
2
/ 2 0.75 0.5
CE X

 
  
 
𝑁 𝐴
𝑁 𝐵
𝑁1𝐶
𝑇𝐴 =
𝑁 𝐴
𝜆
= 2
𝑇𝐵 =
𝑁 𝐵
𝜆
=
12
5
𝑇1𝑐 =
𝑁1𝐶
𝜆/2
= 4

37. Sistema M/M/∞
 Caso especial del sistema M/M/m cuando m tiende a ∞
λ λ λ λ
0 1μ
22μ
λ
mmμ m+1
(m+1)μ3μ
λ
 Sea I=λ/μ entonces, las probabilidades de estado vienen dadas por
𝜆𝑗 = 𝜆 𝑦 𝜇 𝑗 = 𝑗. 𝜇 ∀𝑗
𝜋𝑗 =
𝐼 𝑗
𝑗!
𝜋0 𝜋0 1 +
𝑗=1
∞
𝐼 𝑗
𝑗!
= 1 ⟹ 𝜋0 = 𝑒−𝐼 ⟹ 𝜋𝑗 =
𝐼 𝑗 𝑒−𝐼
𝑗!
𝑁 =
𝑗=0
∞
𝑗 𝜋𝑗 =
𝑗=0
∞
𝑗
𝐼 𝑗
𝑗!
𝑒−𝐼
= 𝐼𝑒−𝐼
𝑗=1
∞
𝐼 𝑗−1
(𝑗 − 1)!
= 𝐼 𝑒−𝐼
𝑒 𝐼
= 𝐼
Nota: 𝑛=0
∞ 𝑥 𝑛
𝑛!
= 𝑒 𝑥
Número de
servidores ocupados
 Por la ley de Little
𝑇 =
1
𝜆
𝑁 =
𝐼
𝜆
=
1
𝜇
= 𝑆 No hay cola!  𝑊 = 𝑄 = 0

38. Sistema M/M/m/m
 Llegadas de Poisson, servicio exponencial, m servidores
idénticos y sin capacidad de almacenamiento
 Usando procesos B-D con λj=λ y μj=j.μ, y tomando I=/ obtenemos
λ
0 1μ
λ
22μ
λ
m-1(m-1)μ
λ
mmμ3μ
λ
𝜋𝑗 =
𝐼 𝑗
𝑗!
𝜋0 para j = 0,1,2, … m
𝜋0 =
𝑗=0
𝑚
𝐼 𝑗
𝑗!
−1
𝜋 𝑚 =
𝐼 𝑚/𝑚!
1 + 𝐼 +
𝐼2
2!
+ ⋯ + 𝐼 𝑚/𝑚!
= 𝐵(𝑚, 𝐼)
Fórmula de pérdidas
de Erlang
 Dado que no hay cola, 𝑊 = 0 y 𝑄 = 0.
 Por tanto, 𝑇 = 1/ y 𝑁 = 𝐼𝑐 = 𝜆(1 − 𝜋 𝑚)/μ

39. Sistema M/G/1
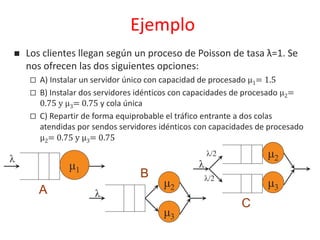
• Llegadas de Poisson, distribución de servicio S
general, servidor único y búfer infinito
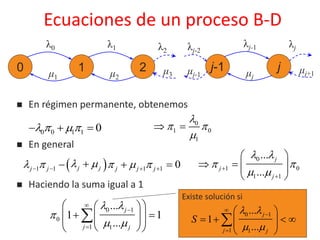
• Según la fórmula de Pollaczek-Khinchine
𝑊 =
𝜆. 𝐸[𝑆2
]
2(1 − 𝜌)
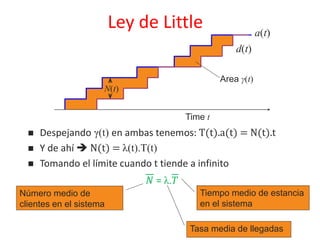
• A partir de ésta, usando la ley de Little, se
obtiene el resto

40. • Dadas las funciones de coste medio por la espera o el servicio:
 WC = Función coste medio por la espera (por unidad de tiempo), que
aumenta con el número de usuarios en el sistema, es decir, disminuye
al aumentar la velocidad media de servicio del sistema
 SC = Función coste medio por el servicio (por unidad de tiempo), que
aumenta con la velocidad media del sistema
 TC = Función Coste medio total (por unidad de tiempo)
• El objetivo es minimizar el coste medio total TC
Minimizando costes
Min TC = WC + SC
Velocidad
de servicio
Coste
WC
SC
TC