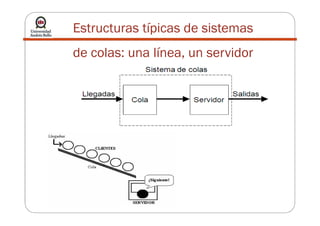
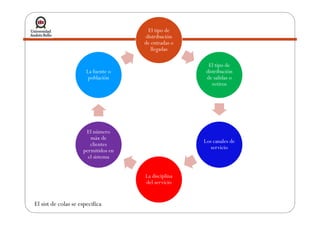
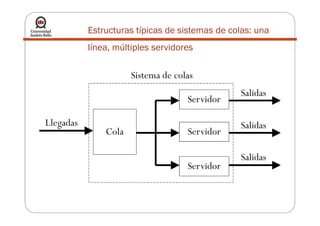
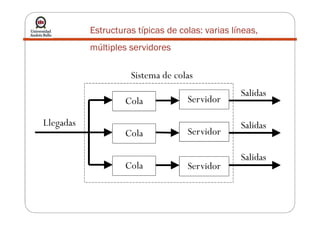
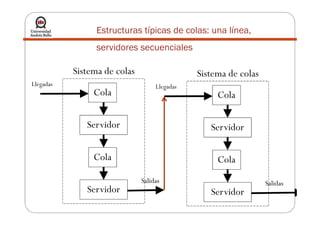
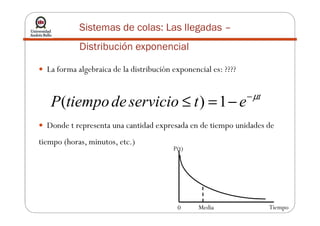
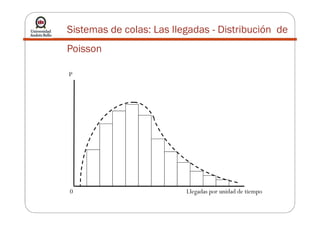
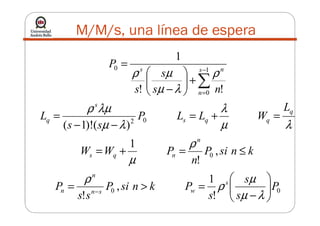
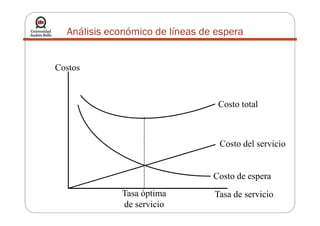
La teoría de colas describe sistemas de líneas de espera mediante modelos matemáticos. Se utiliza para modelar el tráfico en redes. Algunos modelos comunes incluyen M/M/1, con llegadas de Poisson y tiempos de servicio exponenciales para un solo servidor. El objetivo es determinar el estado estable del sistema y la capacidad de servicio apropiada.