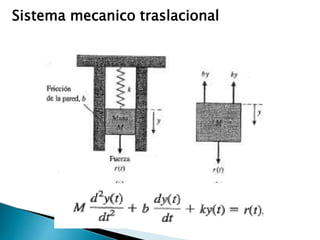
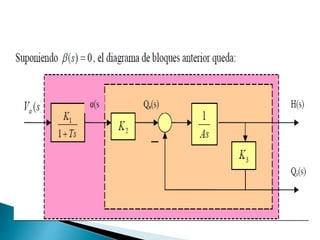
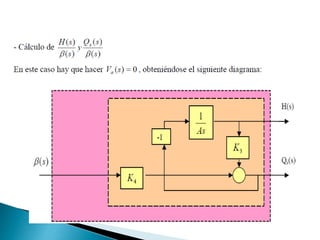
Este documento describe un sistema simplificado de suspensión de automóvil. Explica cómo modelar matemáticamente el movimiento vertical de la suspensión usando ecuaciones diferenciales. El objetivo es obtener la función de transferencia que relaciona el desplazamiento de entrada con el desplazamiento de salida.

5. Sistema mecanico traslacional

9. La figura (a) muestra un diagrama esquemático
de un sistema de suspensión de un automóvil.
Conforme el automóvil avanza por un camino,
los desplazamientos verticales de las llantas
funcionan como una excitación de movimiento
para el sistema de suspensión del automóvil.
El movimiento de este sistema consiste en un
desplazamiento traslacional del centro de la
masa y un desplazamiento de rotación alrededor
del centro de la masa. El modelado matemático
del sistema completo es muy complicado.

11. Una versión muy simplificada del
sistema de suspensión aparece en la
figura (b). Suponiendo que el
movimiento xi en el punto P es la
entrada al sistema y el movimiento
vertical x0 del cuerpo es la salida,
obtenga la función de transferencia
X0(s)/Xi(s). (Considere el movimiento
del cuerpo sólo en la dirección
vertical.) El desplazamiento x0 se
mide a partir de la posición de
equilibrio en ausencia de la entrada

13. Un sistema de suspensión
simplificada de un automóvil se
puede representar por la figura
siguiente:
Las ecuaciones diferenciales que
modelan al sistema están dadas
por:
   
  






















dt
t
dx
dt
t
dy
b
t
x
t
y
k
dt
t
y
d
m
t
x
t
u
k
dt
t
dx
dt
t
dy
b
t
x
t
y
k
dt
t
x
d
m
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
2
2
2
1
2
2
2
1
Obtener la función de transferencia Y(s)/U(s)

19. Se asume que la temperatura de la cámara y, y
el flujo de vapor q s e relacionan por:
Se asume que c es una constante positiva

24. Considérese el sistema térmico representado en la figura
consiste en tres capacitancias térmicas
interconectadas mediante tres resistencias.
Supóngase que la entrada es un flujo de
calor q0(t) y se desea conocer el flujo de
calor q3(t).

25. El cambio de temperatura de un cuerpo
de masa M, cuando recibe un flujo neto de
calor q, está dado por
cp es el calor específico del cuerpo y T su temperatura.
Ct = Mcp se denomina capacitancia térmica
SOLUCION

26. para las capacitancias térmicas se obtiene:
y para las resistencias térmicas:

30. Obtenga la función de transferencia en lazo
cerrado para el sistema de control de posición de
la figura . Suponga que la entrada y la salida del
sistema son la posición de la flecha de entrada y la
posición de la flecha de salida, respectivamente.
Suponga los siguientes valores numéricos para las
constantes del sistema:

31. Kl = ganancia del detector de error potenciométrico = 24lπ
Vlrad
Kp = ganancia del amplificador = 10 V/V
Kb = constante de contra fem =
K = constante de par de motor =

42. Use el algebra de bloques para obtener la función de transferencia “Y(s)/U(s)”

55. GRAFICA DE FLUJO DE SEÑAL
Es una representación gráfica de un juego de
ecuaciones algebráicas lineales.
X1=X1
X2=aX1+dX4
X3=bX1+cX2
X4=eX3+fX4
X5=gX4
X1
X2
X3
X4
X5
a
b
c e
d f
g
Nodo de
Entrada
Nodo de Salida
Nodo Mixto

61. Four different loops, two nontouching loops
e
1 a b c d
f
g
h
Y(s)
R(s)
Y(s)
R(s) =
1 – – –
– af bg ch ehgf+
+
afch
abcd ed (1–bg)
Two forward path
Example 2.14

62. Example 2.15
R(s) Y(s)
1 K
1
1
1
1
1 G1(s) G2(s) G3(s)
-1 -1
-1
-1
P1=G1G2G3K; P2=G2G3K; P3=G1G3K
 



 2
1
3
2
1 G
G
G
G
G
La  


 3
2
1
3
2
3
1
2
1 G
G
G
G
G
G
G
G
G
L
L c
b
 
 3
2
1 G
G
G
L
L
L f
e
d
2
3
1
2
1 1
,
1
,
1 G
G 







3
2
1
3
2
3
1
2
1
3
2
1 2
2
1 G
G
G
G
G
G
G
G
G
G
G
G 








 
 
   
1 2 3 2 1 3
1 2 1
Y s G G G K G GG K
R s
  

