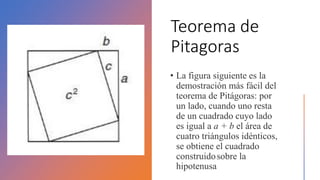
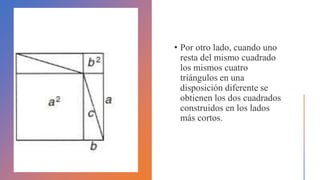
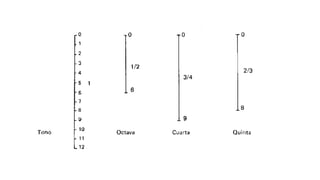
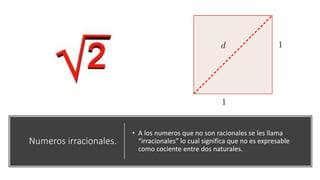
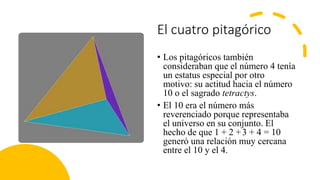
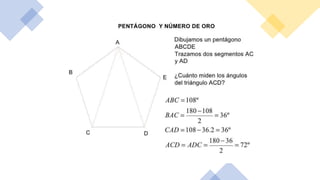
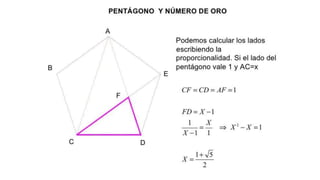
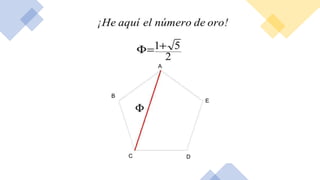
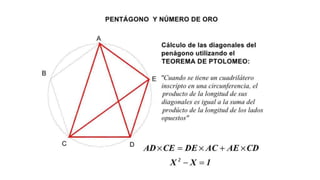
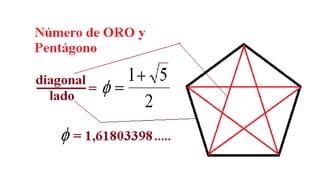
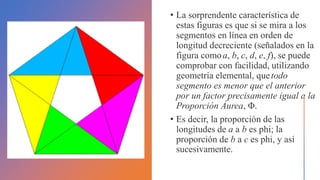
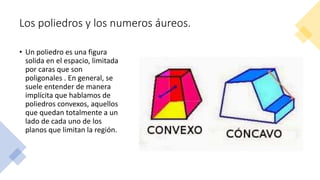
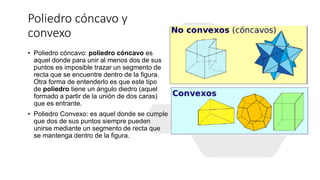
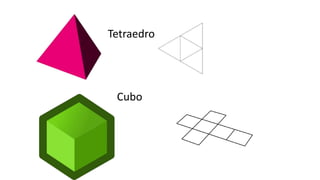
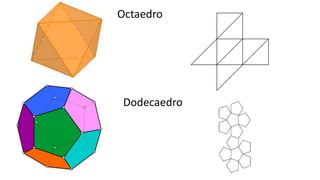
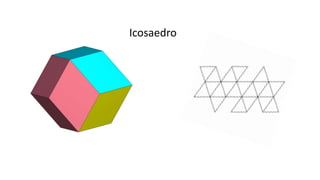
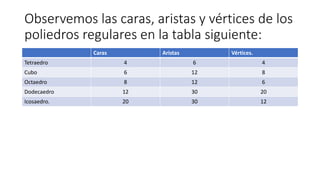
El documento resume la vida y contribuciones de Pitágoras y los pitagóricos. Explica que Pitágoras fundó una escuela en Crotona y que probablemente aprendió matemáticas de sacerdotes egipcios y babilonios. Los pitagóricos hicieron importantes descubrimientos en matemáticas y música, como el teorema de Pitágoras y las proporciones armónicas en cuerdas musicales. También creían que los números tenían propiedades místicas y atribuían cualidades a números específicos como

1. Pitagoras y los pitagóricos
Gabriel Romero Ramirez

2. PITÁGORAS Y LOS PITAGÓRICOS
• Pitágoras nació alrededor del 570 a. C. en la Isla
de Samos, en el mar Egeo, cercade Asia Menor, y
emigró entre el 530 y 510 a Crotona, situada en la
colonia doria delsur de Italia (conocida entonces
como la Magna Grecia). Parece ser que Pitágoras
abandonó Samos para escapar de la represora tiranía
de Polícrates (muerto cerca 522
a. C.), quien estableció la supremacía naval de
Samos en el mar Egeo.

3. Pitagoras y Tales de Mileto
• Quizás siguiendo el consejo de quien se cree
fue su maestro, el matemático Tales de Mileto,
Pitágoras vivió en Egipto durante un tiempo
(unos 22 años según algunas fuentes), donde
habría aprendido de los sacerdotes egipcios
matemáticas, filosofía y temas religiosos.
• Tras la invasión de Egipto por parte de las
tropas persas, Pitágoras pudo haber sido
llevado a Babilonia junto a otros sacerdotes
egipcios. Allí pudo entrar en contacto con la
tradición matemática mesopotámica.

4. • La mayoría de detalles de la vida de
Pitágoras y la realidad de sus contribuciones
matemáticas permanecen tras un velo de
incertidumbre.
• Parece ser que Pitágoras no escribió nada,
perosu influencia fue tan grande que el más
atento de sus seguidores creó una sociedad
secreta o hermandad conocida como los
pitagóricos.
Esta foto de Autor desconocido está bajo licencia CC BY-NC-ND

5. Contribuciones
• Pitágoras y los pitagóricos se
han hecho famosos por su
papel en el desarrollo de las
matemáticas, así como en la
aplicación de las
matemáticas al concepto del
orden, tanto si es orden
musical, orden del cosmos o
el orden ético

6. Todos los niñosaprenden en la escuela el teorema de Pitágoras del
triángulo con un ángulo recto (90 grados), es decir, el triángulo
rectángulo.
• Según este teorema,el área
del cuadrado construido
sobre el lado más largo (la
hipotenusa) es igual a la
suma de las áreas de los
cuadrados construidos en los
lados más cortos.

7. Teorema de Pitagoras
• En otras palabras, si la longitud de la hipotenusa es c,
entonces el área del cuadrado construido
sobre ella es c2; las áreas de los cuadrados construidos
a los otros dos lados (de longitudes a y b) son a2 y b2,
respectivamente.
• El teorema de Pitágoras se puede formular de la siguiente
manera: c2 = a2 + b2 para todos los triángulos rectángulos.

8. Los números 3, 4, 5 o 7, 24, 25, por ejemplo,
forman tripletes pitagóricos porque 32 + 42 = 52 (9
+ + 16 = 25); 72 + 242 = 252, (49 + 576 = 625), y
pueden usarse como longitudes de los lados de un
triángulo rectángulo.

9. Teorema de
Pitagoras

11. •Así, el cuadrado sobre la
hipotenusa es claramente igual
en área a la suma de los dos
cuadrados más pequeños.

12. • Aunque el teorema de Pitágoras aún no era conocido
como una «verdad» que caracteriza a todos los
triángulos de ángulo recto, los tripletes pitagóricos se
habían descubierto mucho antes de la existencia de los
pitagóricos. Una tablilla de arcilla babilónica
procedente del periodo de la Antigua Babilonia (circa
1600 a. C.) contiene 15 de los tripletes mencionados.

13. • Los babilonios descubrieron que los tripletes pitagóricos se pueden
construir usando el siguiente y sencillo procedimiento, o «algoritmo».
• Escoja dos números enteros cualesquiera, p y q, teniendo en cuenta
que p es mayor que q.
• Ahora ya puedeformar el triplete pitagórico de números
• p2 – q2; 2pq; p2 + q2.
• Por ejemplo, supongamos que q es 1 y p es 4.
• Entonces, p2 – q2 = 42 –12 = 16 – 1 = 15; 2pq = 2 × 4× 1 = 8;
p2 + q2 = 42 +12 = 16 +1 = 17.
• El conjunto de números 15, 8, 17 es un
triplete pitagórico porque 152 + 82 = 172, (225 + 64 = 289).

14. • Por lo tanto, existe un número infinito de tripletes
pitagóricos (hecho probado por Euclides de
Alejandría).

15. Pitagoras y la
armonía.

17. Pitagoras y la armonía.
Tan sólo unas pocas combinaciones producen sonidos agradables.
Pitágoras descubrió que estas extrañas consonancias seobtienen cuando
las notas se producen por unas cuerdas similares cuyas longitudes sedan
en una proporción dada por escasos primeros números enteros.
Se obtiene el unísono cuando las cuerdas son:
• de igual longitud una proporción de 1:1.
• la octava se obtiene por una proporción de 1:2 de las longitudes de
cuerda
• la quinta por 2:3
• la cuarta por 3:4

18. Pitagoras y los irracionales.
• Pitagoras sabia que el valor de 2 no era un racional, es decir, que
no podía expresarse como cociente de dos numeros naturales.
• Pero semejante idea contradecía los fundamentos de su
pensamiento, que establecía el numero indivisible y entero como
base del universo.
• Los pitagóricos atribuían al numero un carácter sagrado y creían que
mediante el todo podía medirse, que todo terminaba por ser número

20. • Del mismo modo, 6/5 de una cuerda que da
un Do da la nota La, 4/3 de la misma cuerda da
Sol, 3/2 da Fa, y así sucesivamente.
• Estos antiguos y extraordinarios hallazgos
• formaron la base de un conocimiento más
avanzado de los intervalos musicales que se
desarrolló en el siglo XVI (en los que, por
cierto, Vincenzo Galilei, el padre de Galileo,
estaba involucrado).

21. Pitagoras y los numeros
• Quizás debido a las
sencillas y armónicas
proporciones halladas en
la música, 1:2,2:3, 3:4,
los pitagóricos se
sintieron especialmente
intrigados por las
diferencias entrelos
números pares e
impares.

22. Pitagoras y los numeros.
•Mientras que asociaron los números impares con
los atributos masculinos, además de con la luz y
la bondad (algo evidentemente poco inocente), a
los números pares les otorgaron atributos
femeninos, asociándolos con la oscuridad y la
maldad.

23. Los pitagóricos y los
numeros.
• Para los pitagóricos los numeros
naturales permitían la
explicación del mundo y de toda
la realidad que nos rodea.
• Los numeros naturales
utilizados por medio de razones
o cocientes entre ellos , es decir
fracciones, conforman lo que en
matematicas llamamos
numeros racionales.

24. • La expresión se entiende
pensando que racional tiene
la misma raíz que “ración” ,
que a su vez la comparte con
razón cuando se aplica a una
proporción de dos cantidades.
• Por lo tanto “racional” viene
del termino razón en el
sentido de relacion, no en el
sentido de algo “razonable”
Esta foto de Autor desconocido está bajo licencia CC BY-NC-ND

25. Numeros irracionales.
• A los numeros que no son racionales se les llama
“irracionales” lo cual significa que no es expresable
como cociente entre dos naturales.

26. Los pitagóricos no sólo asignaron cualidades
a los números pares e impares en general,
también atribuyeron propiedades especiales a
números individuales
• Así, se creía que el 1 era el
generador de todos los
números, y no se consideraba
propiamenteun número.
• Además, se creía que
caracterizaba la razón.
• Geométricamente, el número1
se representaba con el punto,
que en sí mismo representaba
el generador de todas las
dimensiones.
Esta foto de Autor desconocido está bajo licencia CC BY-SA

27. El dos Pitagórico.
• El número 2 era el primer número femenino, y también el
número de la opinión y de la división.
Sentimientos parecidos se expresan con el yin y el yangen la
cosmología religiosa china, donde el yin representa el
principio femenino y negativo, como la pasividad y la
oscuridad, y el yang el principio masculino y luminoso.
• Aún hoy en día, en muchas lenguas, el número 2 se
relaciona con la hipocresía y la desconfianza, como puede
verse en expresiones como «doble» (falso),en iraní, o «de
doble lengua», en alemán o árabe.
Esta foto de Autor desconocido está bajo licencia CC BY-NC-ND

28. El tres.
• Se consideraba al tres como el primer número
masculino real y el número de la armonía, ya que
combinaba la unidad (el número 1) y la división (el
número 2). Para los pitagóricos, el 3 era, de algún
modo, el primer número real porque tenía un
«principio», un «medio» y un
• «final» (el 2 sólo tiene un medio). La expresión
geométrica del 3 era el triángulo, ya que tres puntos
que no estén en la misma línea determinan un
triángulo; además, el área del triángulo tiene dos
dimensiones.

29. El tres en la Biblia
• Curiosamente, el 3 fue también la base para la construcción de las
unidades militares en la Biblia. Por ejemplo, en Samuel 2-23 se habla
de los «tres guerreros», una unidad muy básica que tenía el Rey
David.
• En este mismo capítulo se comenta con detalle los «treinta jefes»
que «acudieron a unirse con David en la cueva de Adulam», pero al
final del relato el editor bíblico concluye que «en total eran treinta y
siete». Es obvio que «treinta» era la definición de la unidad, aunque
el número real de sus miembros fuera algo diferente.
• En Jueces 7, cuando Gideón necesita luchar contra los medianitas,
escoge a trescientos hombres, «todos aquellos que pudieran lamer el
agua con sus lenguas». Si nos acercamos a unidades aún mayores, en
Samuel1-13, «Saúl escogió a tres mil de Israel» para luchar contra
los filisteos, que a su vez«lograron reunir a treinta mil carros para
luchar contra Israel». Finalmente, enSamuel 2-6, «David reunió de
nuevo a todos los hombres escogidos de Israel, treinta mil», para luchar contra los
filisteos.
Esta foto de Autor desconocido está bajo licencia CC BY-NC-ND

30. El cuatro Pitagorico
• Para los pitagóricos, el número 4 era el número de la
justicia y el orden.
• En la superficie de la Tierra los cuatro vientos o
direcciones bastaban a los humanos para orientarse e
identificar las coordenadas en el espacio.
• Geométricamente, cuatro puntos que no están en el
mismo plano pueden formar un tetraedro (una pirámide
con cuatro caras triangulares), con un volumen en tres
dimensiones

31. El cuatro pitagórico
• Los pitagóricos también
consideraban que el número 4 tenía
un estatus especial por otro
motivo: su actitud hacia el número
10 o el sagrado tetractys.
• El 10 era el número más
reverenciado porque representaba
el universo en su conjunto. El
hecho de que 1 + 2 +3 + 4 = 10
generó una relación muy cercana
entre el 10 y el 4.

32. El 4
• A su vez, esta relaciónindicaba que 10 no sólo
unía los números que representaban todas las
dimensiones, sino que además combinaba todas
sus propiedades, a saber, lo único (expresado por
el 1), la polaridad (expresada por el 2), la armonía
(expresada por el 3) y el espacio yla materia
(expresadas por el 4).
• Por tanto, el diez era el número de todas las
cosas, con las propiedades que el pitagórico
Filolao expresó tan acertadamente hacia el 400
• a. C.: «sublime, poderoso, creador de todo, el
principio y la guía de lo divino por lo que se
refiere a la vida sobre la Tierra».

33. El cinco pitagórico.
• El cinco representaba la unión del primer
número femenino, 2, conel primer número
masculino, 3, y es el número del amor y el
matrimonio.
• Parece ser que los pitagóricos utilizaban el
pentagrama como símbolo de su hermandad, y
la denominaban «Salud». Luciano, el escritor y
retórico griego del siglo II, escribe lo siguiente
(en En defensa del deslizamiento de lalengua al
saludar):

34. Diosa Higeida
• En 1934, A. de la Fuÿe, en su obra Le Pentagramme
Pythagoricien, Sa Diffusion,Son Emploi dans le Syllabaire
Cuneiform (El pentagrama pitagórico, su difusión y suuso
en el silabario cuneiforme) ofreció una explicación
imaginativa (aunque quizás no del todo acertada) para la
relación entre el pentagrama y la salud.
• De la Fuÿe propuso que el pentagrama simbolizaba a
Higeia, la diosa griega de la salud, a travésde una
correspondencia entre las cinco puntas de la estrella y un
dibujo simple de la diosa

36. La estrella
pentagrama
• La estrella pentagonal es una figura de lo
mas comun en nuestro entorno, Es el
símbolo de la estrella de Hollywood, en el
paseo de la fama de los Ángeles, siendo a su
ves el símbolo de varios partidos
revolucionarios. Sus cinco vértices
representan el internacionalismo asociado
cada uno con un continente. En
combinación con el color rojo, simboliza el
sufrimiento de los oprimidos en su lucha por
la emancipación y la sangre que se derrama
para conseguirlo.
• Su poder simbólico lo hace protagonista de
multitud de banderas , no solo las que
profesan una ideología revolucionaria.
Asoma las banderas de la religión
musulmana, como Marruecos,
representando los cinco mandamientos del
islam. Tambien son pentagonales, las

43. • Y lo que es aún más importante, podemos basarnos en el hecho de que el proceso de
creación de una serie de
pentágonos y pentagramas, unos incluidos dentro de otros, puede continuar
indefinidamente hasta tamaños cada vez más pequeños para demostrar que tanto la
diagonal como el lado del pentagrama son inconmensurables, es decir, que la proporción
de sus longitudes (equivalentes a phi) no puede expresarse como la proporción de dos
números enteros. Esto significa que la diagonal y el lado del pentágono no pueden tener
una medida común, de tal modo que la diagonal es un múltiplo entero de esa medida y el
lado es también un múltiplo entero de la misma medida.
• Recordemos que aquellos números que no pueden expresarse como proporciones de dos
números enteros (es decir, como fracciones o números racionales) se conocen como
números irracionales. Por tanto, esta prueba demuestra que phi es un número irracional.

44. Los poliedros y los numeros áureos.
• Un poliedro es una figura
solida en el espacio, limitada
por caras que son
poligonales . En general, se
suele entender de manera
implícita que hablamos de
poliedros convexos, aquellos
que quedan totalmente a un
lado de cada uno de los
planos que limitan la región.

45. Poliedro cóncavo y
convexo
• Poliedro cóncavo: poliedro cóncavo es
aquel donde para unir al menos dos de sus
puntos es imposible trazar un segmento de
recta que se encuentre dentro de la figura.
Otra forma de entenderlo es que este tipo
de poliedro tiene un ángulo diedro (aquel
formado a partir de la unión de dos caras)
que es entrante.
• Poliedro Convexo: es aquel donde se cumple
que dos de sus puntos siempre pueden
unirse mediante un segmento de recta que
se mantenga dentro de la figura.

46. • Los griegos sabían que hay tantos polígonos regulares como
deseemos (ya que los podemos formar con cualquier numero de
lados) pero poliedros regulares solo hay cinco, los cuales llamamos
solidos platónicos.
• Tres de ellos tienen caras que son triangulos equiláteros: el tetraedro
(cuatro caras), el octaedro (ocho caras) y el icosaedro (veinte caras).
• Uno tiene seis caras cuadradas, el cubo y el ultimo tiene doce caras
que son pentágonos regulares , el dodecaedro. Todos se pueden
inscribir en una esfera.

47. Tetraedro
Cubo

48. Octaedro
Dodecaedro

49. Icosaedro

50. • En la Grecia clásica se asociaba cada uno de estos cuerpos a uno de los
elementos de la naturaleza.
• El cubo representaba la tierra
• El tetraedro representaba el fuego
• El octaedro representaba el aire

51. • El icosaedro el agua
• El dodecaedro el símbolo del cosmos, el universo en su totalidad

52. • La gran atracción de los griegos ,
sobre todo de los pitagóricos por los
poliedros surgió de la
contemplación de minerales
cristalizados muy frecuentes en
Magna Grecia, el sur de la actual
Italia, como los especulares
cristalinos de pirita en forma de
dodecaedro.

53. Observemos las caras, aristas y vértices de los
poliedros regulares en la tabla siguiente:
Caras Aristas Vértices.
Tetraedro 4 6 4
Cubo 6 12 8
Octaedro 8 12 6
Dodecaedro 12 30 20
Icosaedro. 20 30 12

54. Si unimos los centros de las caras de un icosaedro, se
obtiene un dodecaedro.
• El número phi aparece con frecuencia en la relación
entre los sólidos platónicos. En concreto en el
dodecaedro y el icosaedro inscritos en un octaedro.
•
· Si la longitud del lado de un octaedro es L, la
longitud del lado de su dodecaedro inscrito es
L*2*sin(pi/5)/(phi*5) y la de su icosaedro
inscrito es 2*L*phi/6.
• El dodecadro queda también inscrito en el
icosaedro.
· Si multiplicamos por phi la longitud del lado
del dodecaedro inscrito en un icosaedro, la
relación de inscripción se invierte y es el
icosaedro el que pasa a estar inscrito en el
dodecadro.

55. Bibliografía.
• http://diversocracia.org/solid_plato.html
• https://vicmat.com/medidas-relaciones-la-estrella-pitagorica/