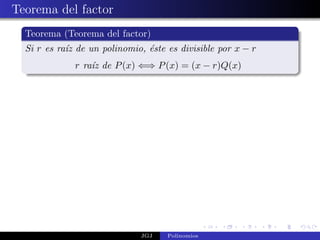
El documento define un polinomio como una expresión formada por la suma de términos que consisten en números multiplicados por potencias de una variable. Explica que el grado de un polinomio se refiere al exponente más alto de dicha variable, y que el coeficiente principal es el número que multiplica a la variable elevada al grado del polinomio. Además, introduce los conceptos de valor numérico de un polinomio para un valor concreto de la variable, así como la noción de raíz de un polinomio.

1. Polinomios
Jes´s Garc´ de Jal´n de la Fuente
u ıa o
IES Avenida de los Toreros
Madrid
jesus.garciadejalon@gmail.com
JGJ Polinomios

2. Polinomios
Definici´n
o
Un polinomio es una operaci´n indicada de sumas y productos
o
entre n´meros y una variable x (indeterminada):
u
P (x) = an xn + an−1 xn−1 + · · · + a1 x + a0
JGJ Polinomios

3. Polinomios
Definici´n
o
Un polinomio es una operaci´n indicada de sumas y productos
o
entre n´meros y una variable x (indeterminada):
u
P (x) = an xn + an−1 xn−1 + · · · + a1 x + a0
n: grado del polinomio
JGJ Polinomios

4. Polinomios
Definici´n
o
Un polinomio es una operaci´n indicada de sumas y productos
o
entre n´meros y una variable x (indeterminada):
u
P (x) = an xn + an−1 xn−1 + · · · + a1 x + a0
n: grado del polinomio
an : coeficiente principal
JGJ Polinomios

5. Polinomios
Definici´n
o
Un polinomio es una operaci´n indicada de sumas y productos
o
entre n´meros y una variable x (indeterminada):
u
P (x) = an xn + an−1 xn−1 + · · · + a1 x + a0
n: grado del polinomio
an : coeficiente principal
a0 : t´rmino independiente
e
JGJ Polinomios

6. Valor num´rico.
e
Definici´n
o
El valor num´rico de un polinomio para x = a es el n´mero que
e u
se obtiene sustituyendo en el polinomio la indeterminada x
por a.
JGJ Polinomios

7. Valor num´rico.
e
Definici´n
o
El valor num´rico de un polinomio para x = a es el n´mero que
e u
se obtiene sustituyendo en el polinomio la indeterminada x
por a.
Sea, por ejemplo, el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
JGJ Polinomios

8. Valor num´rico.
e
Definici´n
o
El valor num´rico de un polinomio para x = a es el n´mero que
e u
se obtiene sustituyendo en el polinomio la indeterminada x
por a.
Sea, por ejemplo, el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
JGJ Polinomios

9. Valor num´rico.
e
Definici´n
o
El valor num´rico de un polinomio para x = a es el n´mero que
e u
se obtiene sustituyendo en el polinomio la indeterminada x
por a.
Sea, por ejemplo, el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
P (−3) = 2 · (−3)4 − 5 · (−3)2 + 4 · (−3) − 2
JGJ Polinomios

10. Valor num´rico.
e
Definici´n
o
El valor num´rico de un polinomio para x = a es el n´mero que
e u
se obtiene sustituyendo en el polinomio la indeterminada x
por a.
Sea, por ejemplo, el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
P (−3) = 2 · (−3)4 − 5 · (−3)2 + 4 · (−3) − 2
= 2 · 81 − 5 · 9 + 4 · (−3) − 2
JGJ Polinomios

11. Valor num´rico.
e
Definici´n
o
El valor num´rico de un polinomio para x = a es el n´mero que
e u
se obtiene sustituyendo en el polinomio la indeterminada x
por a.
Sea, por ejemplo, el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
P (−3) = 2 · (−3)4 − 5 · (−3)2 + 4 · (−3) − 2
= 2 · 81 − 5 · 9 + 4 · (−3) − 2
= 162 − 45 − 12 − 2
JGJ Polinomios

12. Valor num´rico.
e
Definici´n
o
El valor num´rico de un polinomio para x = a es el n´mero que
e u
se obtiene sustituyendo en el polinomio la indeterminada x
por a.
Sea, por ejemplo, el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
P (−3) = 2 · (−3)4 − 5 · (−3)2 + 4 · (−3) − 2
= 2 · 81 − 5 · 9 + 4 · (−3) − 2
= 162 − 45 − 12 − 2
= 103
JGJ Polinomios

13. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
JGJ Polinomios

14. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
JGJ Polinomios

15. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
JGJ Polinomios

16. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
JGJ Polinomios

17. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3
JGJ Polinomios

18. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3
2
JGJ Polinomios

19. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3 –6
2
JGJ Polinomios

20. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3 –6
2 –6
JGJ Polinomios

21. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3 –6 18
2 –6
JGJ Polinomios

22. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3 –6 18
2 –6 13
JGJ Polinomios

23. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3 –6 18 –39
2 –6 13
JGJ Polinomios

24. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3 –6 18 –39
2 –6 13 –35
JGJ Polinomios

25. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3 –6 18 –39 105
2 –6 13 –35
JGJ Polinomios

26. Valor num´rico. Regla de Ruffini(1)
e
El valor num´rico de un polinomio se calcula f´cilmente
e a
mediante la Regla de Ruffini.
Sea de nuevo el polinomio:
P (x) = 2x4 − 5x2 + 4x − 2
Calculemos su valor num´rico para x = −3:
e
2 0 –5 4 –2
–3 –6 18 –39 105
2 –6 13 –35 103
JGJ Polinomios

27. Ra´ de un polinomio
ıces
Definici´n
o
Un n´mero r es ra´ de un polinomio si el valor num´rico del
u ız e
polinomio para x = r es cero.
r ra´ de P (x) ⇐⇒ P (r) = 0
ız
JGJ Polinomios

28. Ra´ de un polinomio
ıces
Definici´n
o
Un n´mero r es ra´ de un polinomio si el valor num´rico del
u ız e
polinomio para x = r es cero.
r ra´ de P (x) ⇐⇒ P (r) = 0
ız
Propiedad: las ra´
ıces enteras de un polinomio con coeficientes
enteros son divisores del t´rmino independiente:
e
JGJ Polinomios

29. Ra´ de un polinomio
ıces
Definici´n
o
Un n´mero r es ra´ de un polinomio si el valor num´rico del
u ız e
polinomio para x = r es cero.
r ra´ de P (x) ⇐⇒ P (r) = 0
ız
Propiedad: las ra´
ıces enteras de un polinomio con coeficientes
enteros son divisores del t´rmino independiente:
e
r ra´ de a0 + a1 x + a2 x2 + a3 x3 + · · ·
ız
JGJ Polinomios

30. Ra´ de un polinomio
ıces
Definici´n
o
Un n´mero r es ra´ de un polinomio si el valor num´rico del
u ız e
polinomio para x = r es cero.
r ra´ de P (x) ⇐⇒ P (r) = 0
ız
Propiedad: las ra´
ıces enteras de un polinomio con coeficientes
enteros son divisores del t´rmino independiente:
e
r ra´ de a0 + a1 x + a2 x2 + a3 x3 + · · ·
ız
=⇒ a0 + a1 r + a2 r2 + a3 r3 + · · · = 0
JGJ Polinomios

31. Ra´ de un polinomio
ıces
Definici´n
o
Un n´mero r es ra´ de un polinomio si el valor num´rico del
u ız e
polinomio para x = r es cero.
r ra´ de P (x) ⇐⇒ P (r) = 0
ız
Propiedad: las ra´
ıces enteras de un polinomio con coeficientes
enteros son divisores del t´rmino independiente:
e
r ra´ de a0 + a1 x + a2 x2 + a3 x3 + · · ·
ız
=⇒ a0 + a1 r + a2 r2 + a3 r3 + · · · = 0
=⇒ a0 = −a1 r − a2 r2 − a3 r3 − · · ·
JGJ Polinomios

32. Ra´ de un polinomio
ıces
Definici´n
o
Un n´mero r es ra´ de un polinomio si el valor num´rico del
u ız e
polinomio para x = r es cero.
r ra´ de P (x) ⇐⇒ P (r) = 0
ız
Propiedad: las ra´
ıces enteras de un polinomio con coeficientes
enteros son divisores del t´rmino independiente:
e
r ra´ de a0 + a1 x + a2 x2 + a3 x3 + · · ·
ız
=⇒ a0 + a1 r + a2 r2 + a3 r3 + · · · = 0
=⇒ a0 = −a1 r − a2 r2 − a3 r3 − · · ·
=⇒ a0 = −r(a1 + a2 r + a3 r2 + · · · )
JGJ Polinomios

33. Ra´ de un polinomio
ıces
Definici´n
o
Un n´mero r es ra´ de un polinomio si el valor num´rico del
u ız e
polinomio para x = r es cero.
r ra´ de P (x) ⇐⇒ P (r) = 0
ız
Propiedad: las ra´
ıces enteras de un polinomio con coeficientes
enteros son divisores del t´rmino independiente:
e
r ra´ de a0 + a1 x + a2 x2 + a3 x3 + · · ·
ız
=⇒ a0 + a1 r + a2 r2 + a3 r3 + · · · = 0
=⇒ a0 = −a1 r − a2 r2 − a3 r3 − · · ·
=⇒ a0 = −r(a1 + a2 r + a3 r2 + · · · )
=⇒ r es divisor de a0
JGJ Polinomios

34. Polinomios primos y compuestos
Son polinomios compuestos los que pueden
descomponerse como producto de polinomios de menor
grado. Por ejemplo x2 − 1 es compuesto porque puede
descomponerse como:
x2 − 1 = (x + 1)(x − 1)
JGJ Polinomios

35. Polinomios primos y compuestos
Son polinomios compuestos los que pueden
descomponerse como producto de polinomios de menor
grado. Por ejemplo x2 − 1 es compuesto porque puede
descomponerse como:
x2 − 1 = (x + 1)(x − 1)
Son polinomios primos los que no pueden descomponerse
como producto de polinomios de menor grado. Por
ejemplo, 3x − 6 o x2 + 1 son polinomios primos.
JGJ Polinomios

36. Polinomios primos y compuestos
Son polinomios compuestos los que pueden
descomponerse como producto de polinomios de menor
grado. Por ejemplo x2 − 1 es compuesto porque puede
descomponerse como:
x2 − 1 = (x + 1)(x − 1)
Son polinomios primos los que no pueden descomponerse
como producto de polinomios de menor grado. Por
ejemplo, 3x − 6 o x2 + 1 son polinomios primos.
Los polinomios primos son los polinomios de primer
grado y los de segundo que no tienen ra´
ıces (los de
discriminante menor que cero). Todos los dem´s pueden
a
descomponerse en factores y son compuestos.
JGJ Polinomios

37. Polinomios primos y compuestos
Son polinomios compuestos los que pueden
descomponerse como producto de polinomios de menor
grado. Por ejemplo x2 − 1 es compuesto porque puede
descomponerse como:
x2 − 1 = (x + 1)(x − 1)
Son polinomios primos los que no pueden descomponerse
como producto de polinomios de menor grado. Por
ejemplo, 3x − 6 o x2 + 1 son polinomios primos.
Los polinomios primos son los polinomios de primer
grado y los de segundo que no tienen ra´
ıces (los de
discriminante menor que cero). Todos los dem´s pueden
a
descomponerse en factores y son compuestos.
JGJ Polinomios

38. Teorema del factor
Teorema (Teorema del factor)
Si r es ra´ de un polinomio, ´ste es divisible por x − r
ız e
r ra´ de P (x) ⇐⇒ P (x) = (x − r)Q(x)
ız
JGJ Polinomios

39. Teorema del factor
Teorema (Teorema del factor)
Si r es ra´ de un polinomio, ´ste es divisible por x − r
ız e
r ra´ de P (x) ⇐⇒ P (x) = (x − r)Q(x)
ız
Demostraci´n.
o
JGJ Polinomios

40. Teorema del factor
Teorema (Teorema del factor)
Si r es ra´ de un polinomio, ´ste es divisible por x − r
ız e
r ra´ de P (x) ⇐⇒ P (x) = (x − r)Q(x)
ız
Demostraci´n.
o
Sea r ra´ del polinomio P (x), es decir, P (r) = 0.
ız
JGJ Polinomios

41. Teorema del factor
Teorema (Teorema del factor)
Si r es ra´ de un polinomio, ´ste es divisible por x − r
ız e
r ra´ de P (x) ⇐⇒ P (x) = (x − r)Q(x)
ız
Demostraci´n.
o
Sea r ra´ del polinomio P (x), es decir, P (r) = 0.
ız
Si se divide P (x) por x − r se obtiene un cociente Q(x) y
un resto R que cumplen:
P (x) = (x − r)Q(x) + R
JGJ Polinomios

42. Teorema del factor
Teorema (Teorema del factor)
Si r es ra´ de un polinomio, ´ste es divisible por x − r
ız e
r ra´ de P (x) ⇐⇒ P (x) = (x − r)Q(x)
ız
Demostraci´n.
o
Sea r ra´ del polinomio P (x), es decir, P (r) = 0.
ız
Si se divide P (x) por x − r se obtiene un cociente Q(x) y
un resto R que cumplen:
P (x) = (x − r)Q(x) + R
Para x = r:
P (r) = (r − r)Q(r) + R =⇒ R = P (r) = 0
y por consiguiente P (x) = (x − r)Q(x).
JGJ Polinomios

43. Teorema del resto
Teorema (Teorema del resto)
El resto de dividir un polinomio por x − a es el valor num´rico
e
del polimomio para x = a.
P (x) = (x − a)Q(x) + R ⇐⇒ R = P (a)
JGJ Polinomios

44. Teorema del resto
Teorema (Teorema del resto)
El resto de dividir un polinomio por x − a es el valor num´rico
e
del polimomio para x = a.
P (x) = (x − a)Q(x) + R ⇐⇒ R = P (a)
Demostraci´n.
o
Si se divide P (x) por x − a se obtiene un cociente Q(x) y un
resto R que cumplen:
P (x) = (x − a)Q(x) + R
Para x = a:
P (a) = (a − a)Q(a) + R =⇒ R = P (a)
JGJ Polinomios

45. Regla de Ruffini(2)
La regla de Ruffini
2 0 –5 4 –2
–3 –6 18 –39 105
2 –6 13 –35 103
JGJ Polinomios

46. Regla de Ruffini(2)
La regla de Ruffini
2 0 –5 4 –2
–3 –6 18 –39 105
2 –6 13 –35 103
puede interpretarse como una divisi´n en la que:
o
Dividendo:
Divisor:
Cociente:
Resto:
JGJ Polinomios

47. Regla de Ruffini(2)
La regla de Ruffini
2 0 –5 4 –2
–3 –6 18 –39 105
2 –6 13 –35 103
puede interpretarse como una divisi´n en la que:
o
Dividendo: 2x4 − 5x2 + 4x − 2
Divisor:
Cociente:
Resto:
JGJ Polinomios

48. Regla de Ruffini(2)
La regla de Ruffini
2 0 –5 4 –2
–3 –6 18 –39 105
2 –6 13 –35 103
puede interpretarse como una divisi´n en la que:
o
Dividendo: 2x4 − 5x2 + 4x − 2
Divisor: x+3
Cociente:
Resto:
JGJ Polinomios

49. Regla de Ruffini(2)
La regla de Ruffini
2 0 –5 4 –2
–3 –6 18 –39 105
2 –6 13 –35 103
puede interpretarse como una divisi´n en la que:
o
Dividendo: 2x4 − 5x2 + 4x − 2
Divisor: x+3
Cociente: 2x3 − 6x2 + 13x − 35
Resto:
JGJ Polinomios

50. Regla de Ruffini(2)
La regla de Ruffini
2 0 –5 4 –2
–3 –6 18 –39 105
2 –6 13 –35 103
puede interpretarse como una divisi´n en la que:
o
Dividendo: 2x4 − 5x2 + 4x − 2
Divisor: x+3
Cociente: 2x3 − 6x2 + 13x − 35
Resto: 103
JGJ Polinomios

51. Factorizaci´n de un polinomio de segundo grado
o
Sea ax2 + bx + c un polinomio de segundo grado.
JGJ Polinomios

52. Factorizaci´n de un polinomio de segundo grado
o
Sea ax2 + bx + c un polinomio de segundo grado.
Seg´n el valor del discriminante:
u
∆ = b2 − 4ac
JGJ Polinomios

53. Factorizaci´n de un polinomio de segundo grado
o
Sea ax2 + bx + c un polinomio de segundo grado.
Seg´n el valor del discriminante:
u
∆ = b2 − 4ac
el polinomio se descompone:
ra´
ıces Factorizaci´n
o
∆>0 r1 , r2 ax2 + bx + c = a(x − r1 )(x − r2 )
∆=0 r ax2 + bx + c = a(x − r)2
∆<0 ax2 + bx + c es primo
JGJ Polinomios

54. Aplicaci´n
o
Una ecuaci´n de tercer grado puede resolverse si se conoce una
o
de las ra´
ıces.
JGJ Polinomios

55. Aplicaci´n
o
Una ecuaci´n de tercer grado puede resolverse si se conoce una
o
de las ra´
ıces.
Sea, por ejemplo, la ecuaci´n x3 − 4x2 − x + 4 = 0.
o
JGJ Polinomios

56. Aplicaci´n
o
Una ecuaci´n de tercer grado puede resolverse si se conoce una
o
de las ra´
ıces.
Sea, por ejemplo, la ecuaci´n x3 − 4x2 − x + 4 = 0.
o
Si sabemos que una soluci´n es x = −1, dividimos el polinomio
o
por x + 1:
JGJ Polinomios

57. Aplicaci´n
o
Una ecuaci´n de tercer grado puede resolverse si se conoce una
o
de las ra´
ıces.
Sea, por ejemplo, la ecuaci´n x3 − 4x2 − x + 4 = 0.
o
Si sabemos que una soluci´n es x = −1, dividimos el polinomio
o
por x + 1:
1 –4 –1 4
–1 –1 5 –4
1 –5 4 0
JGJ Polinomios

58. Aplicaci´n
o
Una ecuaci´n de tercer grado puede resolverse si se conoce una
o
de las ra´
ıces.
Sea, por ejemplo, la ecuaci´n x3 − 4x2 − x + 4 = 0.
o
Si sabemos que una soluci´n es x = −1, dividimos el polinomio
o
por x + 1:
1 –4 –1 4
–1 –1 5 –4
1 –5 4 0
Ahora podemos escribir la ecuaci´n como:
o
(x + 1)(x2 − 5x + 4) = 0
JGJ Polinomios

59. Aplicaci´n
o
Una ecuaci´n de tercer grado puede resolverse si se conoce una
o
de las ra´
ıces.
Sea, por ejemplo, la ecuaci´n x3 − 4x2 − x + 4 = 0.
o
Si sabemos que una soluci´n es x = −1, dividimos el polinomio
o
por x + 1:
1 –4 –1 4
–1 –1 5 –4
1 –5 4 0
Ahora podemos escribir la ecuaci´n como:
o
(x + 1)(x2 − 5x + 4) = 0
e igualando a cero cada factor se calculan las soluciones.
JGJ Polinomios