Este documento describe los números complejos. Explica que los números complejos se pueden representar como la suma de un número real y un número imaginario puro. Define las operaciones de suma, resta, multiplicación y división para números complejos en esta forma binómica. También cubre cómo calcular potencias de números complejos y raíces cuadradas usando esta representación.

1. N´meros complejos
u
1. Cuerpos
Un cuerpo conmutativo es un conjunto de n´meros que pueden sumarse, restarse, multiplicarse y dividirse.
u
Los n´meros racionales, esto es, los n´meros que pueden escribirse en forma de fracci´n, forman un
u u o
cuerpo conmutativo que se representa por la letra Q. Los n´meros reales, formados por los racionales
u
e irracionales, se representan por la letra R y tambi´n tienen estructura de cuerpo conmutativo. Sin
e
embargo el conjunto de los n´meros enteros Z no es un cuerpo pues, en general, los n´meros enteros no
u u
se pueden dividir, por ejemplo, el cociente de 7 entre 3 no es un n´mero entero.
u
De forma m´s precisa, un cuerpo conmutativo F es un conjunto con cuyos elementos pueden hacerse dos
a
operaciones, suma y producto y estas operaciones tienen las propiedades siguientes:
Propiedades de la suma:
1. Asociativa. Para sumar tres elementos pueden asociarse como se quiera
(a + b) + c = a + (b + c)
2. Elemento neutro o cero. Existe un elemento que se le suele llamar cero con la propiedad:
a+0=a
3. Elemento sim´trico u opuesto. Para cada elemento a del cuerpo existe otro elemento (repre-
e
sentado generalmente por −a) con la propiedad de que al sumar ambos se obtiene el elemento
neutro:
a + (−a) = 0
4. Conmutativa. El resultado de la suma es independiente del orden de los sumandos:
a+b=b+a
La existencia de elemento opuesto hace que exista siempre la diferencia de los n´meros. La dife-
u
rencia es la suma de un elemento y el opuesto del otro:
a − b = a + (−b)
Propiedades del producto:
1. Asociativa. Para multiplicar tres elementos pueden asociarse como se quiera
(a · b) · c = a · (b · c)
2. Elemento neutro o unidad. Existe un elemento que se le suele llamar uno con la propiedad:
a·1=a
1

2. ´
2 NUMEROS COMPLEJOS 2
3. Elemento sim´trico o inverso. Para cada elemento a del cuerpo salvo para el cero, existe otro
e
elemento (representado generalmente por a−1 ) con la propiedad de que al multiplicar ambos
se obtiene el elemento unidad:
a · a−1 = 1
4. Conmutativa. El producto es independiente del orden de los factores:
a·b=b·a
La existencia de elemento inverso garantiza que se puedan dividir dos n´meros salvo si el divisor
u
es cero. El cociente es el producto del primer elemento por el inverso del segundo:
a/b = a · b−1
Propiedades de la suma y el producto
Distributiva
a · (b + c) = a · b + a · c
Dado un cuerpo F y un n´mero a no perteneciente al cuerpo, siempre puede encontrarse un cuerpo que
u
contenga a ambos, es decir, al cuerpo F y al n´ mero a. Por ejemplo, si consideramos el √
√ u cuerpo Q de
los n´meros racionales y el n´mero 2 que no es racional, los n´meros de la forma a + b 2 con a y b
u u u √
racionales, forman un cuerpo que incluye a todos los racionales y a 2.
2. N´meros complejos
u
Tanto el conjunto Q de los n´ meros racionales como el conjunto R de los n´meros reales son cuerpos.
u u
La necesidad de ampliar el cuerpo de los racionales, surge del hecho de que muchas funciones, como por
ejemplo las ra´
ıces o el logaritmo, no tienen sentido dentro de este conjunto.
Seg´n hemos visto, en el conjunto de los n´ meros reales tampoco pueden definirse algunas funciones
u u
como la ra´ cuadrada o el logaritmo para n´meros negativos. La ampliaci´n del concepto de n´mero a
ız u o u
los n´meros complejos permite extender el dominio de estas funciones a todos los n´meros.
u u
Para construir los n´meros complejos vamos a a˜adir a los n´meros reales un n´mero i que llamaremos
u n u u
unidad imaginaria y que cumple que i2 = −1, es decir, el n´mero i es una ra´ de −1.
u ız
Si queremos que el nuevo conjunto sea un cuerpo, para que est´ definida la multiplicaci´n, debemos a˜adir
e o n
todos los n´ meros de la forma bi donde b es un n´mero real. Estos n´meros, producto de un n´mero real
u u u u
por la unidad imaginaria, se llaman n´meros imaginarios puros.
u
Adem´s, puesto que los n´meros se pueden sumar, deben existir los n´meros de la forma a + bi donde a
a u u
y b son n´meros reales. Estos n´meros son suma de un n´ mero real y un n´mero imaginario puro.
u u u u
Veremos que con n´meros de la forma a + bi con a, b ∈ R pueden definirse la suma y la multiplicaci´n
u o
con todas las propiedades de un cuerpo conmutativo. Estos n´meros forman el cuerpo de los n´meros
u u
complejos y esta representaci´n de los complejos como suma de un n´mero real y un n´mero imaginario
o u u
puro se llama forma bin´mica del n´mero complejo. El cuerpo de los n´meros se representa por C.
o u u
Por consiguiente, un n´mero complejo a + bi est´ formado por dos n´meros reales a y b. El n´mero a
u a u u
se llama parte real del complejo, y el n´mero b (el que aparece multiplicando a la unidad imaginaria) se
u
denomina parte imaginaria del complejo. Esto es similar a los n´meros fraccionarios que estan compuestos
u
por dos n´ meros enteros, el numerador y? el denominador.
u
De la misma forma que los n´meros reales se representan sobre una recta, los n´meros complejos se
u u
representan en un plano llamado Plano de Argand, tomando la parte real sobre el eje de abscisas (que
llamaremos eje real ) y la parte imaginaria sobre el eje de ordenadas (eje imaginario). El punto represen-
tativo de un n´mero se llama afijo del complejo.
u

3. ´
3 OPERACIONES CON COMPLEJOS EN FORMA BINOMICA 3
En esta representaci´n, los afijos de los n´meros reales est´n sobre el eje de abscisas y los n´meros
o u a u
imaginarios puros sobre el eje de ordenadas. De ah´ los nombres de eje real y eje imaginario con que
ı
designamos estos ejes.
Los complejos que tienen la misma parte real y parte imaginaria del mismo valor y signo contrario, es
decir, los complejos a + bi y a − bi, se llaman conjugados. El conjugado de un complejo z se representa
por z . Los afijos de estos complejos son puntos sim´tricos respecto al eje real. Los n´meros reales son
¯ e u
conjugados de s´ mismos. En la figura siguiente pueden verse los afijos de algunos pares de complejos
ı
conjugados.
3. Operaciones con complejos en forma bin´mica
o
Suma y diferencia. La suma de complejos en forma bin´mica se obtiene sumando las partes
o
reales e imaginarias de los dos complejos:
(a + bi) + (c + di) = a + c + (b + d)i
Por ejemplo:
(−5 + 2i) + (3 − i) = −2 + i
(−5 + 2i) − (3 − i) = −8 + 3i

4. 4 POTENCIA Y RA´ CUADRADA EN FORMA BINOMICA
IZ ´ 4
Producto. Los complejos se multiplican como si fuesen binomios y el polinomio resultante se
reduce teniendo en cuenta que i2 = −1:
(a + bi) · (c + di) = ac + adi + bci + bdi2 = ac − bd + (ad + bc)i
Por ejemplo:
(6 − 2i) · (1 + 5i) = 6 + 30i − 2i − 10i2 = 6 + 28i + 10 = 16 + 28i
El producto de un complejo por su conjugado es un n´mero real positivo. En efecto, sea z = a + bi:
u
z z = (a + bi)(a − bi) = a2 − b2 i2 = a2 + b2
¯
La ra´ cuadrada positiva de este n´mero se llama m´dulo del complejo y se representa por |z|:
ız u o
√
|z| = z z = a2 + b2
¯
Por ejemplo:
√
z = 7 − 5i =⇒ |z| = 72 + 52 = 84
Cociente. La divisi´n de un complejo por un n´mero real es muy sencilla, basta dividir por ese
o u
n´mero tanto la parte real como la parte imaginaria:
u
a + bi a b
= + i
c c c
Si el divisor es un n´mero complejo, puede reducirse al caso anterior multiplicando numerador y
u
denominador por el conjugado del denominador:
a + bi (a + bi)(c − di) ac + bd + (bc − ad)i ac + bd bc − ad
= = = 2 + 2 i
c + di (c + di)(c − di) c2 + d2 c + d2 c + d2
Por ejemplo:
1 + 2i (1 + 2i)(−2 − 3i) −2 − 3i − 4i − 6i2 4 − 7i 4 7
= = = = − i
−2 + 3i (−2 + 3i)(−2 − 3i) 22 + 32 13 13 13
4. Potencia y ra´ cuadrada en forma bin´mica
ız o
La potencia de un n´mero complejo puede calcularse mediante la f´rmula del binomio de Newton:
u o
m m m m−1 m m−2 2 m m
(a + b)m = a + a b+ a b + ··· + b
0 1 2 m
donde


 1 si n=0
m
=
n  m(m − 1)(m − 2) . . . (m − n + 1) si n = 0

n!
estos coeficientes pueden obtenerse tambi´n del tri´ngulo de Tartaglia:
e a
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1

5. 4 POTENCIA Y RA´ CUADRADA EN FORMA BINOMICA
IZ ´ 5
Para un complejo en forma bin´mica, la f´rmula de Newton puede escribirse como
o o
m m m m−1 m m−2 2 2 m mm
(a + bi)m = a + a bi + a b i + ··· + b i
0 1 2 m
Para calcular las potencias de la unidad imaginaria tenemos en cuenta lo siguiente:
i1 =i i5 =i·1=i i9 = i · 1 = i
i2 = −1 i6 = i · i = −1 i10 = i · i = −1
i3 = i · (−1) = −i i7 = i · (−1) = −i i11 = i · (−1) = −i
i4 = i · (−i) = −i2 = 1 i8 = i · (−i) = −i2 = 1 i12 = i · (−i) = −i2 = 1
Puede verse que las potencias de i se repiten en el orden i, −1, −i, 1, y que cuando el exponente es
m´ltiplo de 4 la potencia vale 1. En general, puede escribirse:
u
in = in mod 4
donde n mod 4 significa el resto de dividir n entre 4 (se lee n m´dulo 4).
o
Ejemplo 1 Calcular (2 − 5i)3 .
Aplicando la f´rmula del binomio y teniendo en cuenta que i2 = −1 e i3 = −i:
o
(2 − 5i)3 = 23 − 3 · 22 · 5i + 3 · 2 · 52 i2 − 53 i3
= 8 − 60i − 150 + 125i
= −142 + 65i
Supongamos ahora que queremos calcular la ra´ cuadrada del complejo a + bi, esto es, queremos calcular
ız
un n´mero complejo x + yi que cumpla:
u
(x + yi)2 = a + bi
Desarrollando el cuadrado e igualando la parte real y la parte imaginaria de cada n´mero resulta:
u
x2 − y 2 = a
x2 − y 2 − 2xyi = a + bi =⇒
2xy = b
resolviendo el sistema se obtienen las dos ra´
ıces cuadradas. Hay que recordar que x e y son n´meros
u
reales.
M´s adelante veremos un m´todo mejor para calcular las potencias y ra´
a e ıces de n´meros complejos.
u
√
Ejemplo 2 Calcular la ra´ cuadrada 21 − 20i = x + yi.
ız
√
Sea 21 − 20i = x + yi. Seg´n hemos visto se cumple que
u
x2 − y 2 = 21
2xy = −20
Despejando y en la segunda ecuaci´n y sustituyendo en la primera:
o
−20 −10 100
y= = =⇒ x2 − = 21 =⇒ x4 − 21x2 − 100 = 0
2x x x2
Resolviendo la ecuaci´n bicuadrada se obtiene x = −5 y x = 5. Los valores correspondientes de y son 2 y
o
−2. Por consiguiente, las dos ra´ son −5 + 2i y 5 − 2i. Comprobemos, por ejemplo, el primer resultado:
ıces
(−5 + 2i)2 = 25 − 20i + 4i2 = 25 − 20i − 4 = 21 − 20i

6. ´ ´
5 FORMA POLAR Y TRIGONOMETRICA DEL NUMERO COMPLEJO 6
5. Forma polar y trigonom´trica del n´mero complejo
e u
El afijo de un n´mero complejo puede determinarse, en lugar de por sus coordenadas cartesianas, por
u
´
sus coordenadas polares. Estas son el m´dulo r y el argumento ϕ. El m´dulo es la distancia del afijo del
o o
complejo al origen de coordenadas. Si conocemos la parte real a y la parte imaginaria b del complejo, el
m´dulo es:
o
r= a2 + b2
El m´dulo de un complejo es un n´ mero real positivo. Se suele representar tambi´n escribiendo el complejo
o u e
entre barras, por ejemplo |z|, o |a + bi|.
El argumento de un complejo es el ´ngulo que forma el segmento que une el origen y el afijo del complejo
a
con el semieje real positivo. En realidad, un complejo tiene infinitos argumentos que difieren en un m´ltiplo
u
de 2π, pues si ϕ es un argumento tambi´n lo es ϕ + 2kπ donde k es un n´mero entero. El argumento se
e u
relaciona con la parte real y la parte imaginaria del complejo por:
b
tg ϕ =
a
siempre determinando el ´ngulo teniendo en cuenta el cuadrante en el que se encuentra el afijo del
a
complejo.
Un complejo en forma polar se escribe como rϕ . Por ejemplo 2 π es el complejo que tiene de m´dulo 2 y
3
o
argumento π .
3
√
Ejemplo 3 Calcular el m´dulo y el argumento del n´mero complejo −1 +
o u 3i.
El m´dulo del complejo es:
o
√ √
r = 1+3= 4=2
El afijo del n´mero se encuentra en el segundo cuadrante de modo que el argumento es:
u
√
3 √ π 2π
tg ϕ = = − 3 =⇒ ϕ = π − + 2kπ = + 2kπ (k ∈ Z)
−1 3 3
Si se conocen el m´dulo y el argumento, la parte real y la parte imaginaria se obtienen mediante
o
a = r cos ϕ
b = r sen ϕ

7. ´
6 PRODUCTO Y COCIENTE EN FORMA TRIGONOMETRICA 7
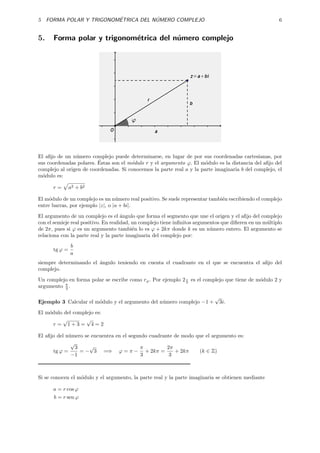
de forma que el complejo a + bi puede escribirse como
a + bi = r cos ϕ + ir sen ϕ = r(cos ϕ + i sen ϕ)
Esta manera de escribir el complejo, sustituyendo r y ϕ en la ultima expresi´n, se llama forma trigonom´tri-
´ o e
ca del n´mero complejo. Por ejemplo, un complejo en forma trigonom´trica ser´ 3(cos π + i sen π ). Este
u e ıa 3 3
complejo tiene de m´dulo 3 y argumento π .
o 3
Ejemplo 4 Calcular la expresi´n en forma bin´mica del complejo de m´dulo 2 y argumento 225o .
o o o
5π
El argumento 225o es igual a 4 radianes. Pasando primero a la forma trigonom´trica tenemos que:
e
√ √
5π 5π 2 2 √ √
2 5π = 2 cos + i sen =2 − −i = − 2 − 2i
4 4 4 2 2
6. Producto y cociente en forma trigonom´trica
e
Sean los complejos:
z1 = r1 (cos ϕ1 + i sen ϕ1 )
z2 = r2 (cos ϕ2 + i sen ϕ2 )
Multipliquemos los dos n´meros:
u
z1 z2 = r1 (cos ϕ1 + i sen ϕ1 ) · r2 (cos ϕ2 + i sen ϕ2 )
= r1 r2 cos ϕ1 cos ϕ2 + i cos ϕ1 sen ϕ2 + i sen ϕ1 cos ϕ2 + i2 sen ϕ1 sen ϕ2
= r1 r2 [cos ϕ1 cos ϕ2 − sen ϕ1 sen ϕ2 + i(sen ϕ1 cos ϕ2 + cos ϕ1 sen ϕ2 )]
= r1 r2 [cos(ϕ1 + ϕ2 ) + i sen(ϕ1 + ϕ2 )]
´
Esta es la forma trigonom´trica de un complejo de m´dulo r1 r2 y de argumento ϕ1 + ϕ2 . Llegamos
e o
por tanto a la siguiente conclusi´n: para multiplicar dos complejos en forma polar o trigonom´trica, se
o e
multiplican sus m´dulos y se suman sus argumentos.
o
No es dif´ imaginar que para dividir complejos se dividir´n sus m´dulos y se restar´n sus argumentos.
ıcil a o a
En efecto, dividamos en forma trigonom´trica multiplicando numerador y denominador por el conjugado
e
del denominador:
z1 r1 (cos ϕ1 + i sen ϕ1 )
=
z2 r2 (cos ϕ2 + i sen ϕ2 )
r1 (cos ϕ1 + i sen ϕ1 )(cos ϕ2 − i sen ϕ2 )
=
r2 (cos ϕ2 + i sen ϕ2 )(cos ϕ2 − i sen ϕ2 )
r1 (cos ϕ1 cos ϕ2 − i cos ϕ1 sen ϕ2 + i sen ϕ1 cos ϕ2 − i2 sen ϕ1 sen ϕ2 )
=
r2 (cos2 ϕ2 + sen2 ϕ2 )
r1 [cos ϕ1 cos ϕ2 + sen ϕ1 sen ϕ2 + i(sen ϕ1 cos ϕ2 − cos ϕ1 sen ϕ2 )]
=
r2
r1 [cos(ϕ1 − ϕ2 ) + i(sen ϕ1 − ϕ2 )]
=
r2
r1
×= [cos(ϕ1 − ϕ2 ) + i(sen ϕ1 − ϕ2 )]
r2
Como hab´ıamos previsto resulta que el complejo cociente de otros dos, tiene como m´dulo el cociente de
o
sus m´dulos y como argumento la diferencia de sus argumentos,
o

8. 7 POTENCIA Y RA´ EN FORMA POLAR
IZ 8
Ejemplo 5 Calcular en forma polar el cociente:
(1 + i)3i
√ √
2 − 2i
En primer lugar, calculamos los complejos en forma polar. Es f´cil ver que:
a
√
1 + i = 2π 4
3i = 3 π
√ √ 4
2− 2i = 2 7π
4
Entonces:
√ √ √ √
(1 + i)3i 2π 3π 3 2 3 2 3 2
√ √ = 4 2
= = =
2 − 2i 2 7π 2 2 2
4+2− 4 −π
π π 7π
4 π
7. Potencia y ra´ en forma polar
ız
Puesto que la potencia de exponente natural no es sino un producto de factores iguales, podemos aplicar
la regla de c´lculo de productos para calcular las potencias: los m´dulos deber´n multiplicarse y los
a o a
argumantos sumarse. Puesto que al multiplicar n veces el m´dulo r por s´ mismo se obtiene rn y al sumar
o ı
el argumento ϕ consigo mismo n veces se obtiene nϕ se tiene que:
n
[r(cos ϕ + i sen ϕ)] = rn (cos nϕ + i sen nϕ)
Si r = 1, la expresi´n anterior se escribe como
o
cos nϕ + i sen nϕ = (cos ϕ + i sen ϕ)n
que se conoce como f´rmula de Moivre. La f´rmula de Moivre permite calcular el seno y el coseno de los
o o
a
´ngulos doble, triple, cu´druple, etc, de un ´ngulo cualquiera ϕ a partir de sen ϕ y cos ϕ.
a a
Ejemplo 6 A partir de la f´rmula de Moivre, obtener cos 3x y sen 3x.
o
Desarrollando la f´rmula de Moivre para n = 3 resulta:
o
(cos 3ϕ + i sen 3ϕ) = (cos ϕ + i sen ϕ)3
= cos3 ϕ + 3 · cos2 ϕ · i sen ϕ + 3 cos ϕ · i2 sen2 ϕ + i3 sen3 ϕ
= cos3 ϕ + 3i cos2 ϕ sen ϕ − 3 cos ϕ sen2 ϕ − i sen3 ϕ
donde se ha tenido en cuenta que i2 = −1 y i3 = −i. Igualando partes reales e imaginarias resulta:
cos 3ϕ = cos3 ϕ − 3 cos ϕ sen2 ϕ
sen 3ϕ = 3 cos2 ϕ sen ϕ − sen3 ϕ
Dado que la ra´ es la funci´n inversa de la potencia, para calcular la ra´ en´sima de un complejo,
ız o ız e
habr´ que extraer la ra´ del m´dulo y dividir el argumento por el ´
a ız o ındice de la ra´ Pero aqu´ es preciso
ız. ı
tener en cuenta que a un complejo le corresponden infinitos argumentos que difieren en un m´ltiplo entero
u
de 2π de forma que
√ ϕ + 2kπ ϕ + 2kπ
n
r(cos ϕ + i sen ϕ) = n
r cos + i sen (k ∈ Z)
n n

9. 7 POTENCIA Y RA´ EN FORMA POLAR
IZ 9
Esto no quiere decir que un complejo tenga infinitas ra´
ıces, una para cada valor de k. Para k = 0 se
obtiene la ra´
ız
√
n
ϕ ϕ
r cos + i sen
n n
ıces diferentes para k = 1, 2, 3, · · · , n − 1 pero para k = n resulta:
Se obtienen ra´
√
n
ϕ + 2nπ ϕ + 2nπ √
n
ϕ ϕ
r cos + i sen = r cos + 2π + i sen + 2π
n n n n
que es igual que la ra´ obtenida para k = 0. De aqu´ deducimos que todo n´mero complejo tiene
ız ı u
exactamente n ra´ ıces en´simas.
e
√
Todas las ra´ de un n´mero complejo rϕ tienen el mismo m´dulo n r. Puesto que el sentido gr´fico del
ıces u o a
m´dulo es la distancia al origen del afijo del complejo, los afijos de todas las ra´ en´simas se encuentran
o √ ıces e
en la circunferencia de centro el origen y radio n r. Las ra´ ıces pueden obtenerse unas de otras sumando
2π
al argumento el ´ngulo n . En el siguiente gr´fico podemos ver las ra´ quintas del n´mero complejo i.
a a ıces u
Ejemplo 7 Calcular las ra´
ıces quintas de i.
√
El n´mero i tiene de m´dulo 1 y argumento π . El m´dulo de todas las ra´ ser´ 5 1. La primera ra´ tiene
u o 2 o ıces a ız
como argumento π : 5 = 10 . Las restantes ra´
2
π
ıces pueden obtenerse de ´sta sumando 2π . As´ obtenemos:
e 5 ı
π π
z1 = cos + i sen
10 10
π 2π π 2π π π
z2 = cos + + i sen + = cos + i sen
10 5 10 5 2 2
π 2π π 2π 9π 9π
z3 = cos + + i sen + = cos + i sen
2 5 2 5 10 10
9π 2π 9π 2π 13π 13π
z4 = cos + + i sen + = cos + i sen
10 5 10 5 10 10
13π 2π 13π 2π 17π 17π
z5 = cos + + i sen + = cos + i sen
10 5 10 5 10 10