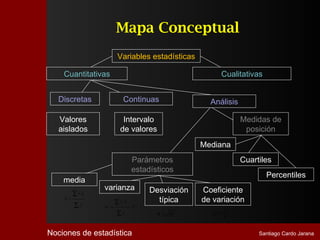
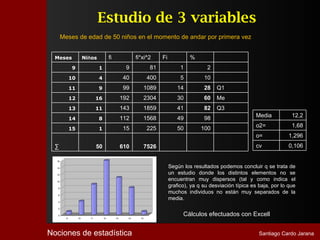
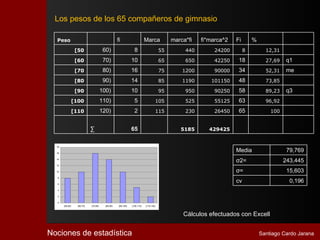
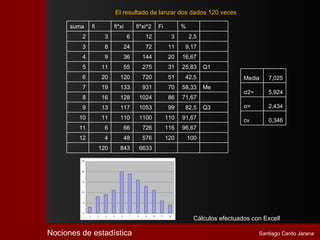
El documento describe la historia y desarrollo de la estadística. Comenzó con registros numéricos simples hace miles de años en civilizaciones como Babilonia y Egipto. Con el tiempo, la estadística se volvió más sofisticada y se utilizó para propósitos como censos y recaudación de impuestos. En el siglo XIX, la estadística se estableció como un método científico para estudiar fenómenos naturales y sociales mediante la reducción de datos a valores numéricos. Hoy en día