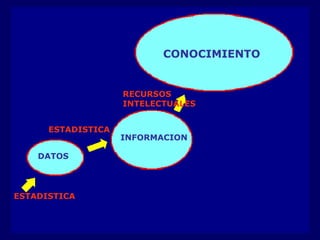
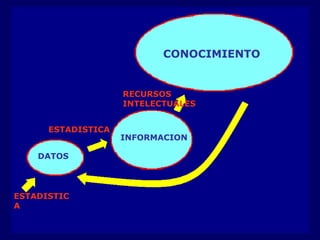
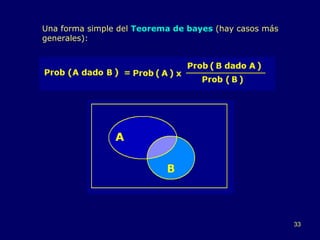
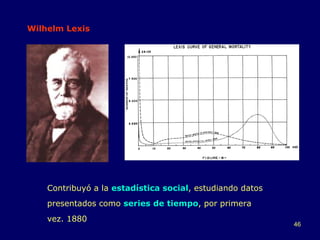
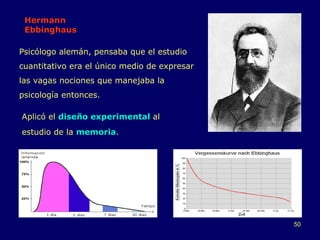
Este documento resume la historia del desarrollo de la estadística desde sus orígenes remotos en el registro de datos por civilizaciones antiguas como Egipto y Babilonia, hasta su evolución como ciencia independiente en los siglos XVIII y XIX con contribuciones de figuras como Gauss, Quetelet y Galton. Destaca hitos como el surgimiento de la teoría de probabilidad en los trabajos de Pascal, Fermat y Huygens, y el desarrollo de métodos estadísticos modernos por parte de Pearson, Neyman y Fisher en el sig

1. DESARROLLO HISTORICO DE LA ESTADISTICA

2. Todo el que toma decisiones debe hacerlo bajo condiciones de incertidumbre , en mayor o menor grado. Con el aumento de la competitividad, la administración de las instituciones requiere tomar decisiones cada vez con una mayor base de conocimiento para así reducir la incertidumbre .

3. Aumento en la eficiencia de los computadores Aumento en la capacidad de almacenar datos. Datos no faltan Pero los datos por si solos no sirven …

4. … si la institución no es capaz de extraer información de ellos. Y con los recursos necesarios, como competencias y experiencia, se puede convertir esta información en conocimiento … … para tomar las decisiones estratégicas, tácticas y operativas.

5. Las etapa de producción de datos y de extracción de información , requiere de métodos , técnicas y herramientas de análisis. El desarrollo de estos métodos, técnicas y herramientas se encuentra en una ciencia que se llama ESTADISTICA .

6. CONOCIMIENTO RECURSOS INTELECTUALES INFORMACION ESTADISTICA ESTADISTICA DATOS

7. CONOCIMIENTO RECURSOS INTELECTUALES INFORMACION ESTADISTICA ESTADISTICA DATOS

8. Godofredo Achenwall , 1760, acuñó la palabra estadística , del italiano statista (estadista), del latín status , estado o situación. Pensaba que la nueva ciencia sería el aliado más eficaz del gobernante.

9. Egipto 3050 AC - Datos sobre población y riqueza. - Ramsés II hizo un censo de las tierras, hacia 1300 AC Antecedentes Remotos de la Estadística

10. También en se guardaban datos de las crecidas del Nilo , que registraban largos períodos de sequía seguidos por largos períodos de inundaciones. Sólo nos llegaron datos desde el año 622 al 1281 de nuestra era, pero hay referencias de que existió esta información desde tiempos remotos. De hecho, construyeron un calendario basado en las crecidas del Nilo.

11. Babilonia 3000 AC - Datos comerciales y agrícolas.

12. Antiguo Israel - La Biblia, libro de los Números: datos estadísticos de dos recuentos de la población. - El rey David, alrededor de 1000 AC, ordenó hacer un censo de Israel.

13. China, 2000 AC - Registros numéricos del bienestar material.

14. Grecia, 540 AC - Censos periódicos con fines tributarios, sociales y militares.

15. Imperio Romano - Censos de población cada cinco años.

16. Francia, 758 y 762 - Relaciones de tierra de la Iglesia, hechas por Pipino el Breve Francia, siglo IX - Censos parciales de la servidumbre de los campos. y por Carlomagno, respectivamente.

17. Inglaterra, 1086. - Censo de Guillermo I: Domesday Book. Inglaterra, siglo XVI. - Registro minucioso de muertes por la peste.

18. Los Censos continúan en nuestros días... ...pero tienen sus días contados.

19. Datos Probabilidad ESTADISTICA

20. La teoría de la probabilidad como una lógica y una metodología para la medición y el estudio de la incertidumbre en la planeación e interpretación de la observación y la experimentación . Es una disciplina matemática que fundamenta la Estadística

21. Una aplicación de la probabilidad empírica a los seguros de buques se encuentra en Flandes, en el siglo XIV.

22. Girolamo Cardano Galileo Galilei 1501-1576 1564-1642 Habían hecho cálculos de probabilidades numéricas , de diversas combinaciones de dados .

23. Pero las raíces de la Teoría de la probabilidad se encuentran en los juegos de azar .

24. Blaise Pascal Los inicios de la probabilidad , como teoría matemática, puede rastrearse en la correspondencia que sostuvo Pascal con Fermat , en la década de 1650.

25. Pierre de Fermat

26. Christian Huygens También los orígenes de la teoría de la probabilidad se encuentran en un corto artículo escrito por él en 1657. Geómetra, físico, astrónomo.

27. Estos trabajos tempranos de Fermat , Pascal y Huygens no abordan problemas de estadística inferencial , o confirmatoria , ni van más allá de los juegos de azar , que eran sus intereses inmediatos.

28. John Graunt es considerado por algunos, como el iniciador de la Estadística , por sus trabajos en demografía , que incorporan nociones de regularidad en el comportamiento de ciertas proporciones de naturaleza aleatoria (1662).

29. Jacob Bernoulli Introduce lo que hoy se conoce como la primera ley de los grandes números . Considerado el iniciador de la teoría de la probabilidad Matemático suizo (n. 1654)

30. Entre los siglos XVIII y XIX , la Estadística se propagó a través de diversas disciplinas: la astronomía y la geodesia , la psicología , la biología , hasta las ciencias sociales . Y también profundizó en el conocimiento del rol de la probabilidad , siendo desplazada la analogía de los juegos de azar, por modelos probabilísticos para efectuar medidas bajo incertidumbre . De este modo se llega a los inicios de la inferencia estadística , cuyo dominio de aplicación se extiende gradualmente, desde fines de este período.

31. Abraham De Moivre Efectuó estudios sobre la ley de probabilidad binomial , y formuló una aproximación para muestras grandes, considerada la primera formulación de la ley de probabilidad normal . 1718 a 1730.

32. Thomas Bayes En 1764 se publicó su trabajo “ Ensayo sobre la Resolución de un Problema en la Doctrina del Azar ” póstumamente. Ignorado por sus contemporáneos, tuvo poca influencia sobre el desarrollo temprano de la Estadística. Sus contenidos sirvieron, casi dos siglos después, para grabar su nombre en la moderna inferencia bayesiana .

33. Una forma simple del Teorema de bayes (hay casos más generales):

34. Una forma simple del Teorema de bayes (hay casos más generales):

35. La inferencia bayesiana es antagónica con la de los frecuentistas , que sólo permiten asignar probabilidades cuando es posible que éstas son apoyadas por experimentación. La inferencia bayesiana permite asignar probabilidades a fenómenos que no son de naturaleza aleatoria , pero cuyos resultados no son conocidos.

36. si se repite un experimento n veces, En la concepción frecuentista de la probabilidad, se registra la fracción de veces que se cumple el evento que nos interesa, E , la probabilidad de E es el límite de esa fracción, cuando n tiende a infinito.

37. Frecuentista esperando que n llegue a infinito.

38. Los Bayesianos permiten que se asigne probabilidad a eventos que no son repetibles . Incluso a eventos que no parecen aleatorios , pero cuyos resultados son desconocidos

39. Arthur Young Publicó sus resultados en 1771, con ideas sorprendentemente modernas sobre el Diseño de Experimentos . Desarrolló un gran número de experimentos agrícolas en su fundo.

40. Pierre Simon Laplace Contribuyó en muchos temas estadísticos, como profundizar la aplicación de la probabilidad a la inferencia , la obtención de una curva de errores , llegando a la formulación de la ley de probabilidad normal . 1774 a 1781.

41. Adrian Marie Legendre Creó un sistema para describir el movimiento planetario, que involucra el método de los mínimos cuadrados , tan utilizado en la Estadística de hoy, como método de estimación de parámetros . 1805. Mínimos Cuadrados fue tema dominante en el siglo XIX.

42. Karl Gauss También contribuyó al método de los mínimos cuadrados . Desembocó en la ley de probabilidad normal independientemente de Laplace, como descripción probabilística del error , pero encontró su asociación con el método de mínimos cuadrados .

43. Adolphe Quetelet Se le ha llamado el padre de la Estadística moderna , por observar la extraordinaria regularidad con que se reproducían ciertos fenómenos sociales , como crímenes o suicidios. 1835. Argumenta que esas regularidades sólo pueden ser encontradas mediante el uso de técnicas estadísticas . Meteorólogo, astrónomo, estadístico, sociólogo. Ajustó distribuciones de probabilidad a datos empíricos.

44. Simeón Denis Poisson Publicó en 1837 el germen de dos elementos asociados a su nombre: La distribución de Poisson . La generalización de la ley de los grandes números de Bernoulli.

45. Numerosos investigadores, provenientes de las más diversas disciplinas , hicieron contribuciones a la Estadística durante la segunda mitad del siglo XIX , construyendo de a poco una disciplina que se iría perfilando cada vez más como una ciencia independiente .

46. Wilhelm Lexis Contribuyó a la estadística social , estudiando datos presentados como series de tiempo , por primera vez. 1880

47. John Arbuthnot Realizó estudios sobre las proporciones de los sexos en los nacimientos. Inglés, médico de la reina Ana.

48. Henry Buckle Inglés, precursor de la moderna Ciencia Histórica , aplicó métodos estadísticos para ayudar de hacer de la historia una ciencia.

49. Gustav Fechner Alemán, con estudios de medicina, aplicó la experimentación para describir relaciones entre estímulos y sensación . Derivó la Estadística hacia la psicología experimental . Introdujo la medición en la psicología , hacia mediados del siglo XIX.

50. Hermann Ebbinghaus Aplicó el diseño experimental al estudio de la memoria . Psicólogo alemán, pensaba que el estudio cuantitativo era el único medio de expresar las vagas nociones que manejaba la psicología entonces.

51. A partir de 1880, Francis Galton , Francis Edgeworth y Karl Pearson , crean una revolución en la Estadística, proporcionando una metodología empírica que sustituye a la experimentación controlada , en disciplinas donde la experimentación no es posible de aplicar. Lo hicieron separadamente Galton en la Antropología , Edgeworth en la Economía y Pearson en la filosofía de la ciencia .

52. Francis Galton (n. 1822) Investigó el carácter hereditario de la genialidad. Investigó la distribución normal bivariada . Fué pionero en el tema de la regresión lineal simple , y por la correlación .

53. Francis Edgeworth Desarrolló una versión del teorema del límite central , que establece que bajo ciertas condiciones, un promedio muestral sigue aproximadamente la ley probabilística normal , si el tamaño muestral es grande Aportó la aproximación de Edgeworth , cuyo uso se ha intensificado hoy. Estudió las aproximaciones que se obtienen cuando los conjuntos de datos crecen .

54. Karl Pearson Estudió las distribuciones probabilísticas asimétricas , Llegando a introducir la distribución Gama . Desarrolló el estadístico ji-cuadrado . Mostró interés en los más diversos temas, además de la estadística, llegando a la convicción de que la estadística analítica yace en los fundamentos de todo el conocimiento. 1892

55. La idea de representatividad , en Estadística, es decir, de seleccionar aleatoriamente algunas unidades para llevar a cabo un estudio sobre una población, es antigua. En esta idea se fundamenta la técnica de muestreo . Sin embargo, durante mucho tiempo no fue aceptado, por la generalidad de los estadísticos.

56. En 1895, fue presentada formalmente en una reunión del Instituto Internacional de Estadística, en Berna, por el director de la Oficina Central de Estadística de Noruega, A. N. Kaier , bajo el nombre de método representativo . Despertó interés pero fue rechazado . Se presentó nuevamente en una reunión del Instituto Internacional de Estadística Roma, en 1926, y finalmente aceptado .

57. Influyeron los trabajos en estudios sociales y económicos, de A. L. Bowley . A él se debe una aplicación de la teoría de inferencia a las encuestas por muestreo , realizado en 1906 .

58. Jerzy Neyman Desarrolló el muestreo de poblaciones finitas , y la estimación por intervalos de confianza . 1934. Estableció que la selección aleatoria es la base de una teoría científica que permite predecir la validez de las estimaciones muestrales . También dejó establecida toda una filosofía sobre la eficiencia de la estrategia muestral .

59. Egon Pearson Hijo de Karl Pearson. Junto a Neyman presentó una teoría sobre cómo probar hipótesis , en base a datos . 1936. Resolvieron dificultades fundamentales para su comprensión, introduciendo las nociones de hipótesis alternativa , y los dos tipos de error , el de rechazar una hipótesis que es verdadera, y el de no rechazar una hipótesis que es falsa. Surge el Lema de Neyman-Pearson .

60. Ronald Fisher Biólogo, genetista y estadístico inglés, ingresó a la estación experimental agrícola de Rotahmsted en 1919. Contribuyó a desarrollar técnicas claves para en la experimentación: La aleatorización , que constituye una protección contra la introducción de factores impredecibles. El diseño experimental en bloques, que permite el control de efectos de factores no deseados.

61. El diseño factorial , para el estudio del efecto de varios factores, simultáneamente. El análisis de varianza , técnica de análisis que permite separar las fuentes de variación y así evaluar su influencia. desarrolló una teoría de estimación eficiente, basada en la Función de Verosimilitud .

62. Se crea una larga controversia entre Ronald Fisher y Neyman y Pearson . Fisher visualizaba la prueba de hipótesis como un procedimiento mediante el cual el investigador podía formarse una opinión sobre alguna característica de la población, o parámetro . Neyman y Pearson vieron la prueba de hipótesis como un medio para que el investigador tomara una decisión sobre un parámetro de la población.

63. William Gosset Químico y matemático inglés. Trabajó como químico en la cervecería Guiness, en particular en Control Estadístico de Calidad . Publicaba sus trabajos de estadística bajo el seudónimo de Student . desarrolló el test T , basado en la distribución de probabilidad T de Student , introducida por él.

64. George Snedecor Fué uno de los pioneros de la Estadística en los Estados Unidos, al constituirse en fundador del Laboratorio de Estadística de la Iowa State University , en 1933, dedicado fundamentalmente a las aplicaciones a la agricultura. Trabajó en conjunto con Ronald Fisher, contribuyendo a desarrollar algunas de las ideas de él. En particular, son importantes sus contribuciones al Análisis de Varianza .

65. William Cochran Nacido en Escocia en 1909. Trabajó en la Iowa State University, junto con Snedecor. Hizo contribuciones al Diseño de Experimentos y a la Teoría del Muestreo . Se trasladó a Rothamsted, Inglaterra, donde tuvo contacto con Ronald Fisher, donde se involucró en aplicaciones médicas de la estadística.

66. Harold Hotelling Economista y Estadístico nacido en 1895. Pionero en la combinación de Estadística Matemática y Economía. También trabajo con Ronald Fisher y aplicó algunas de sus técnicas. En particular al periodismo, ciencia política, demografía y alimentación. Es conocido en Estadística por sus trabajos en Análisis Multivariante , en particular por la distribucion de probabilidad T-Cuadrada de Hotelling , uhna generalización de la T de Student.

67. Frank Wilcoxon Químico y Estadístico nacido en Estados nUnidos en 1892. Contribuyó a la Estadística No-Paramétrica , en particular es suyo el test basado en rangos de Wilcoxon .

68. Charles Spearman Psicólogo nacido en 1863. Se preocupó de definir la inteligencia. Se le considera el primer psicometrista sistemático Fué pionero en el desarrollo del método del Análisis Multivariante denominado Análisis Factorial .

69. L.L. Thurstone Nació en Estados Unidos en 1887. De formación original ingeniero, trabajó junto a Thomas A. Edison . Realizó grandes aportaciones a la medición de la inteligencia y de las actitudes sociales. Defendió la explicación de la inteligencia como conjunto de siete capacidades o factores, también identificables mediante el análisis factorial .

70. Abraham Wald Desarrolló la Teoría Estadística de Decisiones , y la Teoría de Muestreo Secuencial . También en otros campos, como Máxima Verosimilitud Asintótica , Estadística No-Paramétrica , Análisis Discriminante , Control de calidad , Modelos Lineales con Error en las Variables , entre otros.

71. Andrey Kolmogorov Matemático y físico ruso. Planteó los fundamentos de la teoría axiomática de la probabilidad . Hizo contribuciones cruciales a la Teoría Algorítmica de la Aleatoriedad , a la Mecánica Estadística , a los Procesos Estocásticos , a la Teoría de la Información . Analizó la entropía en los texto literarios, lo que dio origen a una corriente de estudios sobre lingüística estadística .

72. Calyampudi Radhakrishna Rao Estadístico Indio nacido en 1920. Hizo contribuciones en las áreas de Teoría de Estimación , Inferencia , Modelos Lineales , Análisis Multivariante , entre otras. Es conocido especialmente por la Cota de Crámer-Rao y el Teorema de Rao-Blackwell .

73. En años recientes ha habido un desarrollo de la Estadística de la mano del computador. Es así como se ha desarrollado la llamada Computación Estadística . El computador permite realizar operaciones repetitivas a alta velocidad. Cuando un problema es demasiado complejo como para encontrar soluciones analíticas, se pueden desarrollar métodos basados en la repetición.

74. Por ejemplo, métodos que buscan aproximaciones a las soluciones óptimas mediante la repetición. Estos métodos dan origen a algoritmos computacionales que requieren mucho procesamiento.

75. Entre estos métodos, están los más conocidos, como el Bootstrap , de B. Efron . El jacknife , la validación cruzada (cross validation), el Gibbs sampling . El Algoritmo EM , de Dempster , Laird y Rubin .

76. Y muchos más, que aún están por descubrirse…..

77. FIN