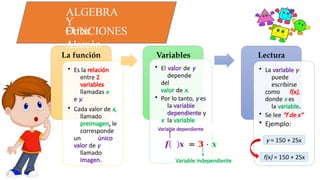
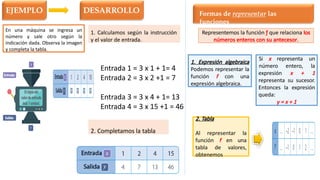
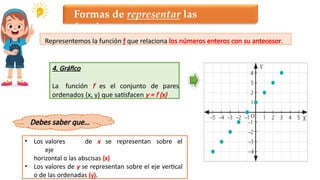
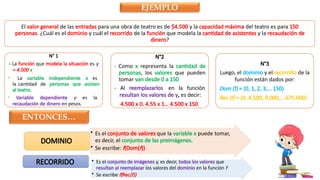
El documento describe la relación entre las variables dependientes e independientes a través de funciones matemáticas, presentando ejemplos de cómo representar funciones mediante expresiones algebraicas, tablas, diagramas y gráficos. Además, aborda el dominio y recorrido de funciones en contextos prácticos, como el cálculo de ingresos en un teatro y la proporcionalidad en el tamaño de letras proyectadas. Se discuten características de funciones lineales, crecientes y decrecientes, así como la forma de calcular pendientes y los conceptos de función afín.

1. La función
• Es la relación
entre 2
variables
llamadas x
e y.
• Cada valor de x,
llamado
preimagen, le
corresponde
un único
valor de y
llamado
imagen.
Variables
• El valor de y
depende
del
valor de x.
• Por lo tanto, y es
la variable
dependiente y
x la variable
independiente
Lectura
• La variable y
puede
escribirse
como f(x),
donde x es
la variable.
• Se lee “f de x”
• Ejemplo:
y = 150 + 25x
f(x) = 150 + 25x
Variable dependiente
𝒇 𝒙 = 𝟑 ⋅ 𝒙
Variable independiente
ALGEBRA
Y
FUNCIONES
Omar
Alarcón

2. EJEMPLO
En una máquina se ingresa un
número y sale otro según la
indicación dada. Observa la imagen
y completa la tabla.
1. Calculamos según la instrucción
y el valor de entrada.
Entrada 1 = 3 x 1 + 1= 4
Entrada 2 = 3 x 2 +1 = 7
Entrada 3 = 3 x 4 + 1= 13
Entrada 4 = 3 x 15 +1 = 46
2. Completamos la tabla
DESARROLLO Formas de representar las
funciones
Representemos la función ƒ que relaciona los
números enteros con su antecesor.
1. Expresión algebraica
Podemos representar la
función f con una
expresión algebraica.
expresión x +
Si x representa un
número entero, la
1
representa su sucesor.
Entonces la expresión
queda:
y = x + 1
2. Tabla
Al representar la
función f en una
tabla de valores,
obtenemos

3. Representemos la función ƒ que relaciona los números enteros con su antecesor.
3. Diagrama
En un diagrama sagital podemos relacionar
los elementos por medio de flechas desde
el conjunto de partida al conjunto de
llegada.
Formas de representar las
funciones

4. Representemos la función ƒ que relaciona los números enteros con su antecesor.
4. Gráfico
La función f es el conjunto de pares
ordenados (x, y) que satisfacen y = f (x)
Formas de representar las
funciones
• Los valores de x se representan sobre el
eje
horizontal o las abscisas (x)
• Los valores de y se representan sobre el eje vertical
o de las ordenadas (y).
Debes saber que…

5. EJEMPLO
El valor general de las entradas para una obra de teatro es de $4.500 y la capacidad máxima del teatro es para 150
personas. ¿Cuál es el dominio y cuál el recorrido de la función que modela la cantidad de asistentes y la recaudación de
dinero?
N° 1
- La función que modela la situación es y
= 4.500 x
- La variable independiente x es
la cantidad de personas que asisten
al teatro.
- Variable dependiente y es la
recaudación de dinero en pesos.
N°2
- Como x representa la cantidad de
personas, los valores que pueden
tomar van desde 0 a 150
- Al reemplazarlos en la función
resultan los valores de y, es decir:
4.500 x 0. 4.55 x 1… 4.500 x 150
N°3
Luego, el dominio y el recorrido de la
función están dados por:
Dom (f) = (0, 1, 2, 3,… 150)
Rec (f) = (0, 4.500, 9.000,… 675.000)
ENTONCES…
• Es el conjunto de valores que la variable x puede tomar,
es decir, el conjunto de las preimágenes.
• Se escribe: f(Dom(f))
DOMINIO
• Es el conjunto de imágenes y, es decir, todos los valores que
resultan al reemplazar los valores del dominio en la función f
• Se escribe f(Rec(f))
RECORRIDO

6. FUNCIÓN LINEAL
• Es una función que puede escribirse de la forma:
¿Qué es?
• Propiedad aditiva
• Propiedad homogénea
Propiedades
𝒇
𝒙
= 𝒎
⋅ 𝒙,
𝒄𝒐𝒏 𝒎 ≠
𝟎
𝒇 𝒙 +
𝒛
= 𝒇 𝒙+
𝒇 𝒛
𝒇 𝒄 ⋅ 𝒙
= 𝒄 ⋅ 𝒇 𝒙 ,
𝒄𝒐𝒏 𝒄
≠ 𝟎

7. EJEMPLO
Se tiene un proyector
que puede triplicar el
tamaño de las letras
según
de un documento
los
requerimientos de los
usuarios. Si se decide
aumentar seis veces el
tamaño original de las
letras de un escrito,
¿Cuál debe ser el
aumento previo?
DESARROLLO
1. El tamaño del documento se relaciona de manera directamente proporcional
con el tamaño de la proyección, por lo tanto podemos representar la función que
modela la proyección del documento.
Función que triplica el tamaño de la letras.
𝒇 𝒙 = 𝟑
⋅ 𝒙
2. Si x representa el tamaño de las letras y a el tamaño con el aumento previo
para que en la proyección el tamaño sea 6 veces el del original, analizamos la
siguiente igualdad
𝒇 𝒂 = 𝟔 ⋅ 𝒙 = 𝟑 ⋅ 𝟐 ⋅ 𝒙 𝐚 = 𝟐 ⋅
𝐱
El doble del tamaño
original de las letras.
3. El tamaño original debe duplicarse para obtener una proyección en
la que el tamaño de las letras sea 6 veces el original.

8. Función lineal
• Función lineal 𝒇 𝒙 = 𝒎 ⋅ 𝒙, 𝒄𝒐𝒏 𝒎 ≠ 𝟎
• Es una recta que pasa por el origen O(0,0)
• El gráfico dependerá del dominio o del conjunto considerado para graficarla.
Valor de m
• Representa al pendiente de la recta
• Si m > 0, la recta es creciente, y si m < 0, la recta es decreciente.
Calcular pendiente
• Si se conocen 2 punto (x,y) y x2, y2 que pertenecen a la grafica de la función f, la
pendiente m se puede calcular de la siguiente forma:
𝐲𝟐
− 𝐲𝟏
𝒎 =𝒙𝟐
− 𝐱𝟏
𝒄𝒐𝒏, 𝒙𝟐
≠

9. EJEMPLO
DESARROLLO
Determina si las funciones f(x)= 2 x y g(x)= -x representan un crecimiento
o un decrecimiento ¿Qué punto tienen en común?
1. Construimos la tabla de valores para cada función
2. Graficamos ambas funciones en el plano
Ambas rectas se
intersectan en el
origen, es decir, el
punto O(0,0)
3. Al observar la representación grafica
• En la función f, es posible notar que los
valores f(x) crecen a medida que los de
x aumentan. Del mismo modo,
lo
valores de g(x) disminuyen a medida
que los de x aumentan.
• La función f representa una función
creciente y la función g representa
una función decreciente.

10. FUNCIÓN AFÍN
= 𝒎 ⋅ 𝒙
+ 𝒄
• Es una función de forma
𝒇 𝒙
• Donde con 𝒎 𝒚 𝒄 𝒔𝒐𝒏
≠ 𝟎
Función lineal
Valor de m
• La constante m es la pendiente.
• c es el coeficiente de posición, el cual corresponde al valor en el eje y por donde
pasa su gráfica.

11. EJEMPLO DESARROLLO
valores de las imágenes ( 𝒇 𝒙
)
La grafica de la función 𝒇 𝒙 = 𝒎
⋅
𝒙 + 𝒄, pasapor los punto A(-2,0) y
B(0,6). Completala tabla con los
y
preimágenes (x) de f.
1. Calculamos la pendiente de la función f
𝒎
=
𝟔−
𝟎
0 − (−2) 2
= 𝟔
=
3
Diferencia entre las ordenadas de los puntos A y B.
Diferencia entre las abscisas de los puntos A y B.
2. Reemplazamos el valor de m en la expresión
𝒇 𝒙 = 𝟑 ⋅ 𝒙 + 𝒄 𝒇 𝟎 = 𝟑 ⋅ 𝟎 + 𝒄 = 𝟔 𝒄
= 𝟔
Luego, se tiene que f3(x) = 𝟑 ⋅ 𝐱 + 𝟔 y al completar la tabla
obtenemos.