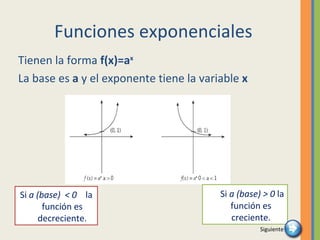
Este documento presenta un resumen de las funciones y gráficas. Explica que una función es una relación entre dos conjuntos donde a cada elemento del dominio le corresponde uno del rango. Describe los tipos de variables en una función y cómo identificar una función mediante la prueba de la recta vertical. Además, provee ejemplos de funciones lineales, cuadráticas, polinomiales, exponenciales y logarítmicas y cómo graficar cada una.

1. Funciones y gráficas Universidad Autónoma de Baja California Facultad de Ciencias Administrativas

2. Haz clic en el enlace que deseas . Temario Carta al estudiante Introducción Graficador

3. Introducción Las funciones son muy importantes en las matemáticas por la gran cantidad de aplicaciones que tienen. Por medio de funciones se puede representar infinidad de situaciones. En la administración de empresas se usan para cálculo de depreciaciones, costos, ingresos, punto de equilibrio financiero, niveles máximos y mínimos de producción, interés compuesto, anualidades, entre otras... Índice

4. Carta al Estudiante Estimado alumno: El siguiente material te ayudará a comprender conceptos fundamentales de la funciones. Lee cuidadosamente cada una de las diapositivas y aprenderás a identificar una función, sus elementos y la gráfica que le corresponde. También encontrarás un graficador en el que solo necesitas introducir los valores que forman la función para ver la gráfica completa, así podrás comprobar lo que aprendiste. ¡ Adelante y Éxito! Índice

5. Temario Elige el tema dando clic en la imagen Índice

6. Concepto de Función Índice Temario Siguiente

7. Función Una función es una relación entre los elementos de 2 conjuntos en la que, a cada elemento del dominio le corresponde solamente uno de los elementos del rango. Siguiente

8. Variables En la función existen dos tipos de variables X Y Variable independiente (en este caso x) que puede tomar diferentes valores Variable dependiente (en este caso y) que depende de los valores tomados por x Siguiente

9. Prueba de la recta vertical Gráficamente el rango se ubica en el eje x y el dominio en el eje y Para saber si una gráfica corresponde a una función, se usa la PRUEBA DE LA RECTA VERTICAL… Consiste en trazar una recta vertical por cualquier parte de la gráfica, Si la recta vertical corta a la gráfica en un solo punto, la gráfica corresponde a una función; caso contrario no. Siguiente

10. Ejercicios de práctica Temario

11. Este diagrama ¿representa una función? 1 2 3 a b X Y SI NO c

12. Excelente El diagrama SI representa una función porque a cada elemento del dominio le corresponde un elemento del rango

13. NO, lo siento El diagrama SI representa una función porque a cada elemento del dominio le corresponde un elemento del rango

14. Este diagrama ¿representa una función? 1 2 a b c X Y SI NO

15. WOW, Muy Bien El diagrama NO es una función porque el elemento 1 del domino tiene dos resultados posibles

16. LO SIENTO El diagrama NO es una función porque el elemento 1 del domino tiene dos resultados posibles

17. Esta tabla de valores ¿representa una función? x y -3 4 0 4 -6 8 0 0 SI NO

18. Genial !!! La tabla NO representa una función porque el elemento 4 tiene dos resultados

19. Sigue intentando La tabla NO representa una función porque el elemento 4 tiene dos resultados

20. Esta gráfica ¿representa una función? SI NO

21. Correcto! Esta gráfica SI representa una función pues al hacer la prueba de la recta vertical vemos que toca a la función en un solo punto

22. Incorrecto Esta gráfica SI representa una función pues al hacer la prueba de la recta vertical vemos que toca a la función en un solo punto

23. Terminaron las preguntas Pregunta anterior Temario

24. Índice Temario Siguiente

25. A Ejemplos Función cuadrática B C Función lineal Función constante D Función Polinomial de grado “n” f(x) = ax 2 +bx+c f(x) = mx+b f(x) = a n x n +a n-1 x n-1 +…+a 2 x 2 +a 1 x+a 0 f(x) = b Observa el exponente de la variable: Si el exponente es uno la función es lineal, si el exponente es dos, la función es cuadrática, si es mayor a 2 la función es polinomial… Ah! Si no tiene variable la función es constante Siguiente

26. Si la VARIABLE ES EL EXPONENTE la función es exponencial Si la variable ACOMPAÑA AL LOGARITMO la función es logarítmica A Ejemplos Función Exponencial B Función logarítmica Siguiente

27. Para graficar Un sistema de coordenadas se forma por la intersección de dos rectas numéricas una horizontal y otra vertical llamados ejes; el punto de intersección se denomina origen. (x,y) x y O Un punto cualesquiera queda representado en este plano por medio de sus coordenadas (x,y) Siguiente II I III IV

28. Gráfica de funciones Graficar una función quiere decir representar en un sistema de coordenadas todos sus pares ordenados. Por ejemplo si la función es y=x 2 / 2 algunos de los pares ordenados serían: (0,0), (2,2), (1, 1 / 2 ), (−2,2) (0,0) (2,2) (1,1/2) (-2,2) Siguiente

29. Funciones lineales Funciones Lineales f(x) = mx + b m ≠ 0 Se llaman así porque su gráfica es una línea recta . m es la pendiente de la recta. b representa el punto donde la recta cruza el eje y (cuando el valor de x=0) se le llama ordenada en el origen. Siguiente

30. Funciones cuadráticas Funciones Cuadráticas f(x) = ax 2 + bx + c a ≠0 Su gráfica es una parábola Si a es positiva la parábola abre hacia arriba, si no, hacia abajo. c representa el punto donde la recta cruza el eje y (cuando el valor de x=0) El vértice es el punto más bajo de la parábola cuando abre hacia arriba y punto más alto cuando abre hacia abajo. Siguiente

31. Funciones polinomiales Funciones Polinomiales El exponente de la variable es mayor a 2 f(x) = f(x) = a n x n +a n-1 x n-1 +…+a 2 x 2 +a 1 x+a 0 Ejemplo: La función cúbica Siguiente

32. Funciones exponenciales Tienen la forma f(x)=a x La base es a y el exponente tiene la variable x Si a (base) < 0 la función es decreciente. Si a (base) > 0 la función es creciente. Siguiente

33. Funciones logarítmicas Tiene la forma: y=log a (x) solo sí x=a y El logaritmo afecta a la variable x Regresar al Temario

35. Índice Temario Siguiente