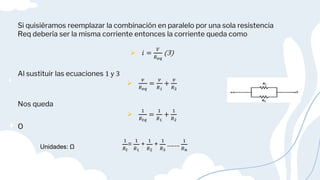
Este documento describe las conexiones en serie y paralelo, las leyes de Kirchhoff y los circuitos RC en serie. Explica que en una conexión en serie todos los componentes comparten la misma corriente, mientras que en una conexión paralelo comparten el mismo voltaje. Las leyes de Kirchhoff establecen que la suma de corrientes que entran a un nodo iguala la suma de corrientes que salen, y que la suma de voltajes en una malla es cero. Finalmente, describe que un circuito RC en serie consta de un resistor y capacitor