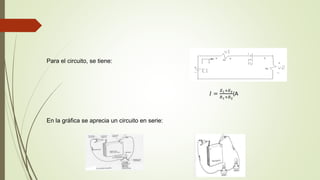
Este documento describe la ley de Ohm y su aplicación en el análisis de circuitos eléctricos. Explica que la ley de Ohm establece la relación entre voltaje, corriente e intensidad a través de un elemento. También describe las leyes de Kirchhoff para análisis de circuitos y cómo usar la ley de Ohm junto con estas leyes para determinar voltajes y corrientes desconocidas. Además, explica el análisis de circuitos RC en serie y la carga y descarga de un condensador en un circuit

1. CAPITULO V
LEY DE OHM Y RESOLUCIÓN DE CIRCUITOS.-

2.  LEY DE OHM.-
La ley de Ohm establece la relación que hay entre las
magnitudes: voltaje, corriente y resistencia a través de
un elemento.
Debe considerarse en un elemento que la corriente
fluye por él, cuando la diferencia de potencia del punto
pon donde entra es mayor que por donde sale,
estableciendo en los extremos una diferencia de
potencia.
En análisis de circuitos se utiliza mucho la regla
nemotécnica de la ley de ohm expresada de la forma
siguiente: 𝑉 = 𝑅 ∗ 𝐼 (𝑉

3. En la parte superior del triángulo,
siempre se tiene el voltaje y en la parte
inferior, sin importar el orden, se coloca
la resistencia y la intensidad.
Para que sea útil el triángulo anterior, se
debe aprender a interpretarlo:
I - Se deseamos conocer el valor del
voltaje se dibuja el triángulo mágico, y
pondremos el pulgar sobre la letra que
representa la magnitud que deseamos
calcular; en este caso será la letra V. Y
nos quedará la fórmula que
necesitamos:
𝑉 = 𝑅 ∗ 𝐼

4. – Si lo que se desea es conocer la
intensidad de corriente, se observa el
triángulo y se coloca la el dedo
tapando la letra I, obteniéndose:
– Si lo que se desea es conocer el valor de la
resistencia, se observa el triángulo y se coloca
la el dedo tapando la letra R, obteniéndose:
𝑅 =
𝑉
𝐼

5. Ley de Ohm y su aplicación en los circuitos de corriente continua:
Ahora se está en condiciones de analizar un circuito serie y poder determinar la corriente que fluye
por el mismo, así como determinar las caídas de tensión en los diferentes elementos que lo
constituyen.
Del circuito siguiente:
 E= RI
I =
𝐸
𝑅
(A)
E…………. representa las fuentes electromotrices colocadas en la malla.
R………… representa las resistencias conectadas entre los terminales de la fuente de tensión.
E= V

6. La corriente I por el circuito es:
I =
𝐸
𝑅1+𝑅2
(A)
Para cuando se tiene varias fuentes electromotrices en la malla, se debe
considerar que la corriente cuando atraviesa una fuente de menos a más
produce un aumento de voltaje y cuando lo hace en sentido contrario,
produce una disminución del mismo. Por tanto las fuentes de voltaje se
pueden conectar para producir un aumento del voltaje o una reducción del
mismo.

7. Para el circuito, se tiene:
𝐼 =
𝐸1+𝐸2
𝑅1+𝑅2
(A
En la gráfica se aprecia un circuito en serie:

8. Un ejemplo en el que se determina la
corriente por la ley de ohm, se observa
en el esquema que ha sido simulado
en el MULTISIM:
El voltaje en una de las resistencias es:

9. Para determinar la diferencia de potencia entres dos puntos de un circuito serie o paralelo, se
sugiere la siguiente regla:
 Seleccione un recorrido de b al punto a, para determinar la diferencia de potencial 𝑉𝑎𝑏 = 𝑉𝑎 −
𝑉𝑏
 Si al avanzar se topa con una f.e.m y la atraviesa de “-“ a “+”. Será positiva, caso contrario,
será negativa.
 Si al avanzar se topa con una resistencia R y la dirección del recorrido coincide con el de la
corriente, el producto R*I será negativo, caso contrario, será positivo.

10.  Análisis de Circuitos con fuentes
de corriente continua: Leyes de
Kirchoff:
Estable que la suma algebraica en un
nodos es cero en todo instante o que la
suma algebraica de las corrientes que
entran al nodo es igual a las corrientes
que salen del nodo.
Se puede asumir:
 Corrientes que salen del nodo como
negativas ( - )
 Corrientes que entran al nodo ( + )

11.  LEY DE VOLTAJES DE KIRCHOFF.-
Establece que la suma algebraica de las f.e.m alrededor de
una malla es igual a las caídas de tensión en los elementos
resistivos.
En la resistencia la corriente al entrar por el elemento, se marca
como terminal positivo y por donde sale, como terminal
negativo; esto hace que se muestren los signos indicados en la
gráfica; en el caso de las f.e.m, se considera el signo de la
fuente por donde entra la corriente.
Se recorre la malla en la dirección de la corriente y se aplica la
ley de voltajes de kirchoff.
Luego se aplica la ley de ohm en cada elemento:
𝑉 = 𝑅 ∗ 𝐼
Se puede interpretar como:
Suma de caidas de tension = Suma de aumentos de
tensión

13.  PUNTO DE REFERENCIA O DE TIERRA.-
El símbolo de la referencia a tierra se representa por:
Generalmente en algunos sistemas eléctricos por propósitos de
seguridad algunos elementos se conectan a tierra. El voltaje de
referencia a tierra es cero (0).
El voltaje de tierra fija una referencia de forma que se puede
obtener el voltaje de cualquier otro punto del circuito respecto
a tierra.

14. CIRCUITO RC EN SERIE.-
Sea:
𝑽 𝑹 + 𝑽 𝑪 = 𝑬
𝑹𝒊 + 𝑽 𝒄 =
𝑬 ; 𝒊 𝑪 = 𝒊 = 𝑪
𝒅𝑽 𝑪
𝒅𝒕
𝑹 𝑪
𝒅𝑽 𝑪
𝒅𝒕
+ 𝑽 𝑪 = 𝑬
𝑹 𝑪
𝒅𝑽 𝑪
𝒅𝒕
= E- 𝑽 𝑪
𝒅𝑽 𝑪
𝒅𝒕
=
𝟏
𝑹𝑪
𝑬 − 𝑽 𝑪

15. 𝒅𝑽 𝑪
𝑬 − 𝑽 𝑪
=
𝟏
𝑹𝑪
𝒅𝒕
− 𝟎
𝑽 −𝒅𝑽 𝑪
𝑬−𝑽 𝑪
= 𝟎
𝒕 𝟏
𝑹𝑪
𝒅𝒕
𝒍𝒏 (𝑬 − 𝑽 𝒄 𝟎
𝑽 𝑪
= −
𝒕
𝑹𝑪
𝒍𝒏 𝑬 − 𝑽 𝒄 − 𝒍𝒏 𝑬 = −
𝒕
𝑹𝑪
𝒍𝒏
𝑬−𝑽 𝒄
𝑬
= −
𝒕
𝑹𝑪
;
𝑬−𝑽 𝒄
𝑬
= 𝒆−
𝒕
𝑹𝑪
E - 𝑽 𝑪 = 𝑬𝒆−
𝒕
𝑹𝑪
𝑽 𝑪 = 𝑬 𝟏 − 𝒆−
𝒕
𝑹𝑪

16. La velocidad a la cual un capacitor se carga depende del
producto de R y C, al cual se le conoce como la constante
de tiempo del circuito y se representa con el simbolo 𝜏 (la
letra griega tau). RC tiene unidades de segundos.
Entonces,
𝜏 = RC (segundos, s)

17. DESCARGA DE UN CONDENSADOR.-
En el circuito siguiente se tiene:
El condensador ha llegado a su carga y con valor Vc.
𝑅𝐶
𝑑𝑉𝑐
𝑑𝑡
+ 𝑉𝐶 = 0
Al utilizar los conceptos del cálculo integral, se tiene:
𝑅𝐶
𝑑𝑉𝑐
𝑑𝑡
= − 𝑉𝐶 ;
𝑑𝑉𝑐
𝑉𝑐
= −
𝑑𝑡
𝑅𝐶
ln 𝑉𝑐𝑉𝑜
𝑉𝑐
= −
1
𝑅𝐶0
𝑡
; ln 𝑉𝐶/𝑉𝑜 = −
𝑡
𝑅𝐶
𝑽 𝑪(𝒕 = 𝑽𝒐 𝒆−
𝒕
𝑹𝑪 ;
Además: VR = - VC
𝑽 𝑹 = - 𝑽𝒐 𝒆−
𝒕
𝑹𝑪 (A)

18.  𝑖 𝐶 = 𝑖 𝑅 =
𝑉 𝑅
𝑅
= -
𝑽 𝒐
𝑹
𝒆−
𝒕
𝑹𝑪
De lo estudiado se puede expresar las
ecuaciones:
Donde VF y I F ----son los valores finales de
voltaje y corriente
Vi y Ii ------- valores iniciales de voltaje y
corriente

19. Ejemplo)
El interruptor de la figura se cierra en t= 0 s. Si E= 60 V, R = 2 k y C=25 uF, determine las
expresiones para vC e iC.

Al cerrar el interruptor:
𝑉𝐶 = 𝐸 1 − 𝑒−
𝑡
𝑅𝐶 = 60 1 − 𝑒
−
𝑡
2∗25∗10−6 𝑡
𝑉𝐶 = 60 1 − 𝑒−
𝑡
50 ; 𝑡 𝑒𝑛 𝑚𝑠
𝑖 𝑐= C
𝑑𝑣
𝑑𝑡
= 60𝐶 𝑒−
𝑡
50 ∗
1
50
𝑖 𝑐= 30𝑒−
𝑡
50 (mA)