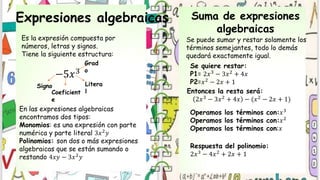
El documento trata sobre expresiones algebraicas. Explica que están compuestas por números, letras y signos, y tienen una estructura con coeficiente, literal, grado y signo. También describe los diferentes tipos de expresiones como monomios y polinomios, y los métodos para sumar, restar, multiplicar y dividir expresiones algebraicas.

1. Expresiones algebraicas
Es la expresión compuesta por
números, letras y signos.
Tiene la siguiente estructura:
Signo
Coeficient
e
Litera
l
Grad
o
En las expresiones algebraicas
encontramos dos tipos:
Monomios: es una expresión con parte
numérica y parte literal 3𝑥2
𝑦
Polinomios: son dos o más expresiones
algebraicas que se están sumando o
restando 4𝑥𝑦 − 3𝑥2
𝑦
Suma de expresiones
algebraicas
Se puede sumar y restar solamente los
términos semejantes, todo lo demás
quedará exactamente igual.
Se quiere restar:
P1= 2𝑥3 − 3𝑥2 + 4𝑥
P2=𝑥2 − 2𝑥 + 1
Entonces la resta será:
2𝑥3 − 3𝑥2 + 4𝑥 − (𝑥2 − 2𝑥 + 1)
Operamos los términos con:𝑥3
Operamos los términos con:𝑥2
Operamos los términos con:𝑥
Respuesta del polinomio:
2𝑥3
− 4𝑥2
+ 2𝑥 + 1
−5𝑥3

2. Multiplicación de
polinomios
En la multiplicación, se deben multiplicar
todos los términos entre si:
Se quiere multiplicar:
P1=𝑥2
− 2𝑥 + 1
P2=𝑥3
+ 2𝑥2
+ 5𝑥 + 8
Entonces: 𝑥2
− 2𝑥 + 1 ∗ 𝑥3
+ 2𝑥2
+ 5𝑥 + 8
Se multiplica el primer término del primer
polinomio por cada uno de los términos del
segundo polinomio:
𝑥2
∗ 𝑥3
= 𝑥5
𝑥2
∗ 2𝑥2
= 2𝑥4
𝑥2
∗ 5𝑥 = 5𝑥3
𝑥2 ∗ 8 = 8𝑥2
Ahora se multiplica el segundo
término del primer polinomio:
−2𝑥 ∗ 𝑥3
= −2𝑥4
−2𝑥 ∗ 2𝑥2 = −4𝑥3
−2𝑥 ∗ 5𝑥 = −10𝑥2
−2𝑥 ∗ 8 = −16𝑥
Se multiplica el tercer término
del primer polinomio:
1 ∗ 𝑥3 = 𝑥3
1 ∗ 2𝑥2
= 2𝑥2
1 ∗ 5𝑥 = 5𝑥
1 ∗ 8 = 8
Ahora se acomoda la respuesta para
lo cual hay que recordar que los
términos semejantes se suman o se
restan
𝑥5
+ 2𝑥4
− 2𝑥4
+ 5𝑥3
− 4𝑥3
+ 𝑥3
+ 8𝑥2
− 10𝑥2
+ 2𝑥2
− 16𝑥 + 5𝑥 + 8
La respuesta es: 𝑥5 + 2𝑥3 − 11𝑥 + 8

3. División sintética
Es el método para efectuar la
división de polinomios, siempre y
cuando el divisor sea de la forma
ax+b que sea lineal con grado 1.
Pasos:
- Se determina para que el valor
de x el divisor es cero x=-b/a
- Se hace la división sintética
usando –b/a como factor.
- El resultado que de el cociente
baja un grado respecto al
polinomio original y se divide
entre a.
- El último término es el residuo.
Ejemplo
s:

4. Productos
notables
Los productos notables son
multiplicaciones especiales entre
expresiones algebraicas, que se
destacan de las demás multiplicaciones
y hacen que un producto sea notable y
se cumplen ciertas reglas que hay que
tener en cuenta:
Fórmulas de
factorización
Factorización
Presenta un polinomio en factores y
es el paso contrario a los productos
notables, es una descomposición en
factores de una expresión
algebraica en forma de producto.
Cuadrado de la suma de dos
cantidades:
(𝑎 + 𝑏)2
= 𝑎2
+ 2𝑎𝑏 + 𝑏2
Cuadrado de la diferencia de dos
cantidades:
(𝑎 − 𝑏)2 = 𝑎2 − 2𝑎𝑏 + 𝑏2
Diferencia de cuadrados:
𝑎2
− 𝑏2
= 𝑎 + 𝑏 𝑎 − 𝑏
Trinomio de la forma 𝑥2
+ 𝑏𝑥 + 𝑐
Trinomio de la forma 𝑎𝑥2
+ 𝑏𝑥 + 𝑐
Factor común
Método por agrupación

5. Simplificació
n
Para simplificar se factorizan
tanto el numerador como el
denominador en factores primos,
para después cancelar los factores
comunes.
Elementos de una función
Dominio:
son los elementos del conjunto de
partida, es decir, los elementos de X
que corresponden a la variable
independiente.
Imagen:
son los elementos del conjunto de
llegada, es decir, los elementos de Y
y que corresponden a la variable
dependiente.
Regla o condición:
se considera a la forma en que se
relacionan los elementos de X y Y,
se debe tener en cuenta que a cada
elemento de X le corresponde solo

6. 𝟑(𝒙 + 𝟐)𝟐 − 𝟐(𝒙 − 𝟐)𝟐
Para desarrollar la expresión
algebraica aplicaremos la formula del
cuadrado de la suma de dos cantidades
o binomio al cuadrado(𝒂 + 𝒃)𝟐
= 𝒂𝟐
+
𝟐𝒂𝒃 + 𝒃𝟐
𝟑(𝒙 + 𝟐)𝟐
− 𝟐(𝒙 − 𝟐)𝟐
(se aplica la
fórmula del binomio al cuadrado)
𝑥2 + 2𝑥 ∗ 2 + 22 (se simplifica)
𝑥2
− 4𝑥 + 4
3 𝑥2
+ 4𝑥 + 4 − 2 𝑥2
− 4𝑥 ∓ 4
(operar)
3 𝑥2 + 4𝑥 + 4 → 3𝑥 − 12𝑥 + 12
= 3𝑥2 + 12𝑥 + 12 𝑥2 − 4𝑥 + 4
−2 𝑥2
− 4𝑥 + 4 → −2𝑥2
+ 8𝑥 − 8
= 3𝑥2 + 12𝑥 − 2𝑥2 + 8𝑥 − 8
Se simplifica y el resultado queda de
la siguiente manera
𝑥2 + 20𝑥 + 4

7. Tarea 2
De la siguiente lista de polinomios
R(x)= 𝑥2 – 4
S(x)= (2x − 3)2
N(x)= 𝑥2 -2x +1
M(x)= 𝑥3 +2𝑥2 +5x +8
Q(x) = 4𝑥5 − 6𝑥4 +2𝑥3 + 9𝑥2− 12x
P(x) = 2𝑥3 - 3𝑥2 + 4x
Realizar la siguiente operación:
1. P(x) – N(x)
𝟐𝒙𝟑
− 𝟑𝒙𝟐
+ 𝟒𝐱 − 𝒙𝟐
− 𝟐𝒙 + 𝟏
𝟐𝒙𝟑 − 𝟑𝒙𝟐 + 𝟒𝐱
Coeficiente: 2,3,4
Literal: x
Signo: +,-
Grado: 3,2
−𝒙𝟐 − 𝟐𝒙 + 𝟏
Coeficiente: 2
Literal: x
Signo: -,+
Grado: 2
𝟐𝒙𝟑 − 𝟑𝒙𝟐 + 𝟒𝐱 − 𝒙𝟐 −2x +1
2𝑥3 − 4𝑥2 + 2𝑥 + 1

8. Tarea 3
Realizar la siguientes división de
polinomios aplicando la división
sintética
(𝒙𝟐 + 𝒙𝟐 − 𝟓𝒙 − 𝟐) ÷ (𝒙 − 𝟐)
𝟔𝒙𝟒 + 𝟕𝒙𝟑 − 𝟔𝒙𝟐 + 𝟕𝒙 − 𝟐) ÷ (𝟑𝒙 − 𝟏)

9. Tarea 4
Determinar el valor de la variable x en la
siguiente expresión algebraica.
𝟐𝒙𝟐 − 𝟐
𝒙 + 𝟏
+
𝟕𝒙 + 𝟒
𝒙 + 𝟐
− 𝟐𝒙 = 𝟑
Simplificar el primer término
2𝑥2
− 2
𝑥 + 1
→ 𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑟
2 𝑥 − 1
2 𝑥 − 1 +
7𝑥 + 4
𝑥 + 2
− 2𝑥 = 𝟑
𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑟 𝑎𝑚𝑏𝑜𝑠 𝑙𝑎𝑑𝑜𝑠 𝑝𝑜𝑟 𝑥 + 2
2 𝑥 − 1 𝑥 + 2 +
7𝑥 + 4
𝑥 + 2
𝑥 + 2 − 2𝑥 𝑥 + 2 = 3 𝑥 + 2
Simplificar
𝟕𝒙 + 𝟒
𝒙 + 𝟐
𝒙 + 𝟐 = 𝟕𝒙 + 𝟒
2 𝑥 − 1 𝑥 + 2 + 7𝑥 + 4 − 2𝑥 𝑥 + 2 = 3 𝑥 + 2
Resolver 2 𝑥 − 1 𝑥 + 2 + 7𝑥 + 4 − 2𝑥 𝑥 + 2
= 5𝑥
Resolver 3𝑥 + 2 = 3𝑥 + 6
5𝑥 = 3𝑥 + 6 𝑅𝑒𝑠𝑡𝑎𝑟 3𝑥 𝑑𝑒 𝑎𝑚𝑏𝑜𝑠 𝑙𝑎𝑑𝑜𝑠
5𝑥 − 3𝑥 = 3𝑥 + 6 − 3𝑥 → 𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑟
2𝑥 + 6 → 𝑑𝑖𝑣𝑖𝑑𝑖𝑟 𝑎𝑚𝑏𝑜𝑠 𝑙𝑎𝑑𝑜𝑠 𝑒𝑛𝑡𝑟𝑒 𝑑𝑜𝑠
2𝑥
2
=
6
2
→ 𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑟
𝑥 = 3

10. Tarea 5
Determine el dominio de la siguiente
función.
Para encontrar el dominio de una
función racional se debe encontrar los
valores que hacen cero el denominador
y quitárselo a ℝ
𝑓 𝑥 =
𝑥 − 2
(𝑥 + 1)(𝑥 − 3)
→
El denominador debe ser distinto a
cero
𝑥 + 1 ≠ 0 𝑥 − 3 ≠ 0
𝑥 ≠ −1 𝑥 ≠ 3 →
El dominio de la función es
𝑥 < −1 𝑜 − 1 < 𝑥 < 3 𝑜 𝑥 > 3
Por lo tanto el dominio es
−∞, −1 𝑢 −1,3 𝑢 (3, ∞)

11. Tarea 6
𝒎𝟐 − 𝟒𝒎 + 𝟑; 𝟐𝟕 − 𝒙𝟑𝒚𝟑
𝒎𝟐
− 𝟒𝒎 + 𝟑
1. Multiplicar el coeficiente del
primer término por la constante
1 ∗ 3 = 3
2. Encontrar los factores de 3 cuya
suma es igual al coeficiente del
término medio, que es -4
3. Reescribir el polinomio
dividiendo el termino medio
usando los dos factores
encontrados en el paso 2, -3
𝑚2 − 3𝑚 − 1𝑚 − 3
4. Sumar los dos primeros términos
extrayendo factores similares 𝑚 ∗
𝑚 − 3
Sumar los términos y extraer
factores comunes 1 ∗ 𝑚 − 3
5. Sumar los cuatro términos
𝟐𝟕 − 𝒙𝟑𝒚𝟑
Diferencia de cubos perfectos
𝑎 − 𝑏 ∗ 𝑎2 + 𝑎𝑏 + 𝑏2
27 𝑒𝑠 𝑒𝑙 𝑐𝑢𝑏𝑜 𝑑𝑒 3
𝑥3 𝑒𝑠 𝑒𝑙 𝑐𝑢𝑏𝑜 𝑑𝑒 𝑥1
𝑦3 𝑒𝑠 𝑒𝑙 𝑐𝑢𝑏𝑜 𝑑𝑒 𝑦1
La factorización es
3 − 𝑥𝑦 ∗ (9 + 3𝑥𝑦 + 𝑥2𝑦2)

12. Tarea 7
Simplificar la siguiente expresión
algebraica
51𝑎𝑑
60𝑏𝑐
∗
48𝑎𝑏
27𝑐𝑑
Para efectuar la expresión algebraica
se debe multiplicar las fracciones de
la siguiente manera
𝑎
𝑏
∗
𝑐
𝑑
=
𝑎∗𝑐
𝑏∗𝑑
51𝑎𝑑 ∗ 48𝑎𝑏
60𝑏𝑐 ∗ 27𝑐𝑑
𝑒𝑙𝑖𝑚𝑖𝑛𝑎𝑟 𝑡𝑒𝑟𝑚𝑖𝑛𝑜𝑠 𝑐𝑜𝑚𝑢𝑛𝑒𝑠 ∶ 𝑑
51𝑎 ∗ 48𝑎𝑏
60𝑏𝑐 ∗ 27𝑐
𝑒𝑙𝑖𝑚𝑖𝑛𝑎𝑟 𝑙𝑜𝑠 𝑡𝑒𝑟𝑚𝑖𝑛𝑜𝑠 𝑐𝑜𝑚𝑢𝑛𝑒𝑠: 𝑏
R𝑒𝑠𝑜𝑙𝑣𝑒𝑟 51𝑎 ∗ 48𝑎
2448𝑎2
60𝑐 ∗ 27𝑐
𝑅𝑒𝑠𝑜𝑙𝑣𝑒𝑟 60𝑐 ∗ 27𝑐
2448𝑎2
1620𝑐2
→ 𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑟
68𝑎2
45𝑐2

13. Ramírez, V. A. P., & Cárdenas, A. J. C.
(2001). Matemática universitaria:
conceptos y aplicaciones generales.
Vol. 1. San José, CR: Editorial Cyrano.
Páginas 59 - 82. https://elibro-
net.bibliotecavirtual.unad.edu.co/es/
ereader/unad/85383?page=66
Rondón, J. (2005) Matemática
Básica. Bogotá D.C.: Universidad
Nacional Abierta y a
Distancia. http://hdl.handle.net/1059
6/7425