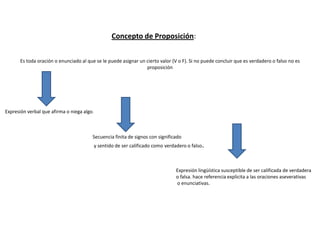
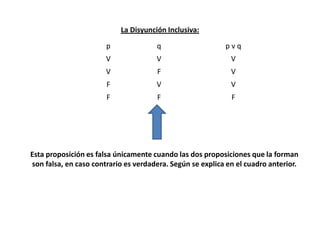
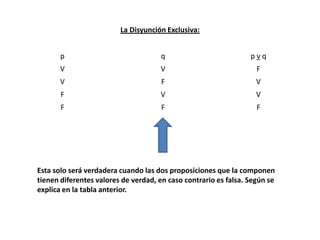
Este documento define conceptos básicos de lógica proposicional como proposiciones, conectivos lógicos, tablas de verdad, y leyes del álgebra proposicional. Explica que una proposición es una expresión que puede ser evaluada como verdadera o falsa, y que los conectivos lógicos como "y", "o", "si...entonces...", relacionan proposiciones simples para formar proposiciones compuestas. También presenta tablas de verdad para los conectivos y resume nueve leyes del ál

1. Republica Bolivariana de Venezuela
Universidad Fermín Toro
Facultad de Ingeniería
Alumno: Toro M, Carlos J
C.I: 14.315.621
Tutor: Domingo Méndez

2. Concepto de Proposición:
Es toda oración o enunciado al que se le puede asignar un cierto valor (V o F). Si no puede concluir que es verdadero o falso no es
proposición
Expresión verbal que afirma o niega algo.
Secuencia finita de signos con significado
y sentido de ser calificado como verdadero o falso.
Expresión lingüística susceptible de ser calificada de verdadera
o falsa. hace referencia explicita a las oraciones aseverativas
o enunciativas.

3. Conectivos lógicos de una proposición:
En Lógica - Matemática no hay dudas para decidir. Solo existen Verdadero o Falso, pero para esto, se siguen reglas que
determinan la Verdad o Falsedad; en este caso de acuerdo a la tabla de contenidos se puede deducir lo siguiente:
Operador o conectivo lógico Son letras o palabras que enlazan dos o más proposiciones simples para formar proposiciones
compuestas, ejemplos:
p: En el teatro están Carlos y Lucho.
q: En el teatro no está Carlos. (la palabra de negación es un caso especial).
r: En el teatro está Carlos o Lucho.
s: Si en el teatro está Carlos, entonces, está Lucho.
t: En el teatro está Carlos si y solo si está Lucho.
Entonces :
• 1. p ^ q: En el teatro están Carlos y Lucho
• Además, VL(p ^ q) = 1, ya que VL(p)= 1 y VL(q)= 1.
• 2. q ^ r: en el teatro esta Carlos o Lucho ,y Miranda nació en Coro.
• Además, VL(q ^ r) = 0, ya que VL(q)= 1 y VL(r)= 0.

4. La Disyunción Inclusiva:
p q pvq
V V V
V F V
F V V
F F F
Esta proposición es falsa únicamente cuando las dos proposiciones que la forman
son falsa, en caso contrario es verdadera. Según se explica en el cuadro anterior.

5. La Disyunción Exclusiva:
p q pvq
V V F
V F V
F V V
F F F
Esta solo será verdadera cuando las dos proposiciones que la componen
tienen diferentes valores de verdad, en caso contrario es falsa. Según se
explica en la tabla anterior.

6. El Condicional:
Una proposición condicional es aquella que esta constituida por dos proposiciones simples, (o compuesta) p y q; es la
combinación de dos proposiciones unidas por la conectiva “si…entonces…”, que se representa de la forma siguiente: “→“. La
proposición que aparece entre las palabras ”Si y Entonces”, se denomina antecedente o hipótesis y la que aparece después de la
palabra “Entonces”, se le llama consecuente o conclusión. la cual se indica de la siguiente manera:
P q Se lee “Si p entonces q”
Se Representa: p q p→q
V V V
V F F
F V V
F F V

7. La Bicondicional
Esta solo es verdadera cuando las dos proposiciones que la forman tiene el mismo valor de verdad, es decir, cuando las dos
proposiciones que la forman ambas sean verdaderas o ambas falsas. En caso contrario la Bicondicional es falsa.
Se Representa:
p q pðq
V V V
V F F
F V F
F F V

8. Leyes del Algebra Proposicional:
• Las leyes de la algebra de proposiciones son equivalencias lógicas que se pueden demostrar con el desarrollo de las tablas de verdad del
bicondicional. Las leyes del algebra de proposiciones son las siguientes:
• 1. EQUIVALENCIA
• P⇔P
• 2. INDEPOTENCIA
• P∧P ⇔P
• P∨ P ⇔P
• 3. ASOCIATIVA
• P∨Q ∨R ⇔ (P∨Q) ∨R ⇔ P∨(Q∨R)
• P∧Q ∧R ⇔ (P∧Q) ∧R ⇔ P∧(Q∧R)
• 4. CONMUTATIVA
• P∧Q⇔ Q∧P
• P∨Q⇔ Q∨P Algunas aplicaciones en matemática e Ingeniería
• 5. DISTRIBUTIVAS
• P∧(Q∨R)⇔ (P∧Q)∨(P∧R) - Demostración Directa
• P∨(Q∧R)⇔(P∨Q)∧(P∨R) - -Demostración Indirecta
• 6. IDENTIDAD - Método del Contrareciproco
• P∧F ⇔ F - Demostración por reducción al Absurdo
• P∧V⇔ P
• P∨F⇔ P
• P∨V⇔V
• 7. COMPLEMENTO
• P∧¬P⇔F
• P∨¬P⇔V
• ¬(¬P)⇔P
• ¬F⇔V
• ¬V⇔F
• 8. DE MORGAN
• ¬(P∧Q)⇔ ¬P∨¬Q
• ¬(P∨Q)⇔¬P∧¬Q
• 9. ABSORCION