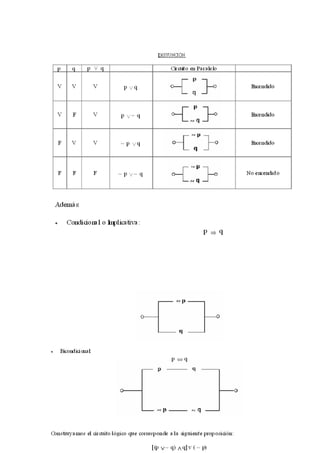
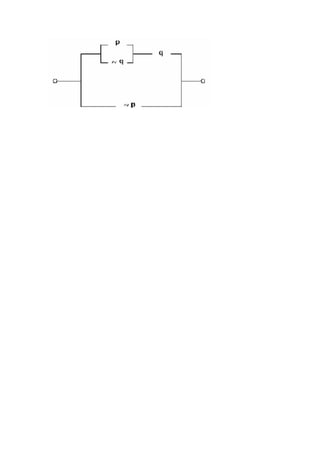
Este documento presenta información sobre conceptos lógicos como proposiciones, clasificaciones de proposiciones, tablas de verdad, tautologías, contradicciones y leyes del álgebra de proposiciones. Explica que una proposición es una oración que puede ser verdadera o falsa, pero no ambas. Clasifica proposiciones en simples y compuestas, y describe conectivos lógicos como la negación, conjunción, disyunción, condicional y bicondicional.

1. Republica Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación
Vicerrectorado Académico
Universidad Fermín Toro
Integrantes
Sergio Méndez
C.I:20.669.292
Cabudare, 7 de noviembre del 2012

2. Una proposición es una oración declarativa de la cual podemos asegurar que es
verdadera o que es falsa, pero no ambas situaciones a la vez.
Las proposiciones se clasifican en:
Proposiciones simples o atómicas son aquellas que constan de un solo
enunciado.
Proposiciones compuestas o moleculares son las que constan de dos o más
proposiciones simples entrelazadas por ciertas particularidades lógicas llamadas
conectivos lógicos.
También existen las clasificaciones de las proposiciones compuestas las cuales
son:
La Negación: la conectiva “no” es la que se antepone a una proposición para
cambiar su valor de verdad y se representa por el siguiente símbolo “~”.
La Conjunción: es una proposición compuesta que se obtiene al unir dos
proposiciones simples unidas o entrelazadas mediante el conectivo “y”, y se
representa con el siguiente símbolo: “ð”.
La Disyunción Inclusiva: es una proposición compuesta de dos proposiciones
simples unidas por el conectivo lógica “o”, que se representa de la manera
siguiente: “V”.
La Disyunción Exclusiva: es una proposición compuesta por dos proposiciones
simples entrelazas por el conectivo “o…o” y se representa así: “V”.
La Condicional o Implicación: es la combinación de dos proposiciones unidas
por la conectiva “si…entonces…”, que se representa de la forma siguiente: “→“.
La proposición que aparece entre las palabras “Si y Entonces”, se denomina
antecedente o hipótesis y la que aparece después de la palabra “Entonces”, se le
llama consecuente o conclusión.
La Bicondicional o Doble Implicación: es una proposición que se obtiene al unir
dos proposiciones simples mediante el conectivo “si y solo si” y se representa
así:”ð”.
Las funciones compuestas también están conformadas por una valor de verdad el
cual es:
La Negación: si una proposición (sea simple o compuesta) es verdadera, su negación es
falsa y viceversa. Ejemplo: si Pes: “Constanza es un municipio de la Vega”, ~ P se
leerá: “no es cierto que Constanza es un municipio de la Vega”.
La Conjunción: esta proposición solo es verdadera cuando las dos proposiciones que la
forman son verdaderas, y en los demás casos será falsa.
La Disyunción Inclusiva: esta proposición es falsa únicamente cuando las dos
proposiciones que la forman son falsa, en caso contrario es verdadera.

3. La Disyunción Exclusiva: esta solo será verdadera cuando las dos proposiciones que la
componen tienen diferentes valores de verdad, en caso contrario es falsa.
La Condicional o Implicación: una condicional solo es falsa cuando su antecedente es
verdadero y el consecuente es falso; en lo demás casos la condicional es verdadera.
La Bicondicional o Doble Implicación: esta solo es verdadera cuando las dos
proposiciones que la forman tiene el mismo valor de verdad, es decir, cuando las dos
proposiciones que la forman ambas sean verdaderas o ambas falsas. En caso contrario la
Bicondicional es falsa.
De igual forma cada proposición compuesta costa de su respectiva tabla de la verdad
que son las siguientes:
Negación:
p ~p
V F
F V
Conjunción:
p q pðq
V V V
V F F
F V F
F F F
Disyunción Inclusiva:
p q pvq
V V V
V F V
F V V
F F F

4. Disyunción Exclusiva:
p q pvq
V V F
V F V
F V V
F F F
Condicional o Implicación:
p q p→q
V V V
V F F
F V V
F F V
Bicondicional o Doble Implicación:
p q pðq
V V V
V F F
F V F
F F V
CONCEPTO DE TAUTOLOGIA
Una proposición compuesta es lógicamente verdadera o tautológica cuando es verdadera
siempre, independientemente de los valores de verdad de las proposiciones simples que
la forman. Ejemplo:
p q pvq p→( p v q)
V V V V
V F V V
F V V V
F F F V

5. CONCEPTO DE CONTRADICCION
La contradicción: es una proposición compuesta que es falsa independientemente de los
valores de verdad de las proposiciones que la formen. Ejemplo:
p ~p pðq
V F F
F V F
CONCEPTO DE CONTINGENCIA
La contingencia: es la combinación de la tautología y la contradicción. Ejemplo :
p q p→q
V V V
V F F
F V V
F F V
Las proposiciones también poseen leyes llamadas leyes del algebra de proposiciones
Las leyes de la algebra de proposiciones son equivalencias lógicas que se pueden
demostrar con el desarrollo de las tablas de verdad del bicondicional. Las leyes del
algebra de proposiciones son las siguientes:
1. EQUIVALENCIA
P⇔P
2. INDEPOTENCIA
P∧P ⇔P
P∨ P ⇔P
3. ASOCIATIVA
P∨Q ∨R ⇔ (P∨Q) ∨R ⇔ P∨(Q∨R)
P∧Q ∧R ⇔ (P∧Q) ∧R ⇔ P∧(Q∧R)
4. CONMUTATIVA
P∧Q⇔ Q∧P
P∨Q⇔ Q∨P
5. DISTRIBUTIVAS
P∧ (Q∨R) ⇔ (P∧Q) ∨ (P∧R)
P∨ (Q∧R) ⇔ (P∨Q) ∧ (P∨R)

6. 6. IDENTIDAD
P∧F ⇔ F
P∧V⇔ P
P∨F⇔ P
P∨V⇔V
7. COMPLEMENTO
P∧¬P⇔F
P∨¬P⇔V
¬ (¬P) ⇔P
¬F⇔V
¬V⇔F
8. DE MORGAN
¬ (P∧Q) ⇔ ¬P∨¬Q
¬ (P∨Q) ⇔¬P∧¬Q
9. ABSORCION
P∧ (P∨Q) ⇔P
P∨ (P∧Q) ⇔
Se pueden realizar circuitos lógicos usando proposiciones estos se hacen de la siguiente
forma:
Un circuito lógico es un conjunto de símbolos y operaciones que satisfacen las reglas de
la lógica, simulando el comportamiento real de un circuito eléctrico.
Circuito en serie:
Sean los interruptores P y Q; su conexión en serie (en una misma línea), dada por:
En este circuito pasara corriente solo en caso que P y Q se encuentren cerrados. Así
tenemos el comportamiento de la conjunción: