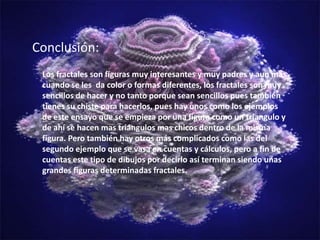
Los fractales son objetos cuya estructura se repite a diferentes escalas y siempre se ven igual sin importar la distancia, como el triángulo de Sierpinski que se construye repitiendo triángulos más pequeños dentro de uno grande. El conjunto de Mandelbrot es un fractal más complejo definido por valores numéricos que generan sucesiones, mostrando patrones geométricos distintos para cada valor. Aunque algunos fractales son sencillos de hacer repitiendo figuras, otros como el conjunto de Mandelbrot se basan en cálculos numéricos.

1. Fractales

2. Que son los fractales:
Un fractal es un objeto cuya estructura se repite a diferentes
escalas. Es decir, por mucho que nos acerquemos o alejemos del
objeto, observaremos siempre la misma estructura. De
hecho, somos incapaces de afirmar a qué distancia nos
encontramos del objecto, ya que siempre lo veremos de la misma
forma.
El termino fractal (del Latín fractus) fue propuesto por el
matemático Benoît Mandelbrot en 1975. En la naturaleza
encontramos muchas estructuras con geometría fractal. Existen
muchísimos fractales, ya que como veremos, son muy fáciles de
construir. Los ejemplos más populares son el conjunto
“Mandelbrot” o el triángulo “Sierpinski”.

3. El “Sierpinski” se realiza de una forma muy
sencilla: dibujamos un triángulo
grande, colocamos otros tres triángulos en su
interior a partir de sus esquinas, repetimos el
último paso.

4. Como hacer un fractal:
Como puede verse, la estrategia más sencilla para conseguir un
fractal, es coger una figura y reproducirla en versiones más pequeñas.
Sin embargo, se pueden conseguir objetos muchos más complejos.
El conjunto de Mandelbrot fue propuesto en los años setenta, pero no
fue hasta una década más tarde cuando pudo representarse
gráficamente con un ordenador. Este conjunto se define a partir de un
número “c” cualquiera, que define la siguiente sucesión:

5. Para diferentes valores de “c”, obtenemos diferentes sucesiones. Si
la sucesión es acotada, “c” pertenece al conjunto de Mandelbrot, y
si no, queda excluido. Por ejemplo, para c=1 se obtiene:
0, 1, 2, 5, 26, 677, etc.(0, 1=02+1, 2=12+1, 5=22+1, etc.) Para c=-0.5
obtenemos 0, -0.5, -0.25, -0.4375, -0.30859375, -0.404769897, etc.
De esta forma, c=-0.5 pertenece al conjunto y c=1 no.
Si además consideramos números complejos, obtenemos la
siguiente figura:

6. Conclusión:
Los fractales son figuras muy interesantes y muy padres y aun mas
cuando se les da color o formas diferentes, los fractales son muy
sencillos de hacer y no tanto porque sean sencillos pues también
tienes su chiste para hacerlos, pues hay unos como los ejemplos
de este ensayo que se empieza por una figura como un triangulo y
de ahí se hacen mas triángulos mas chicos dentro de la misma
figura. Pero también hay otros más complicados como las del
segundo ejemplo que se vasa en cuentas y cálculos, pero a fin de
cuentas este tipo de dibujos por decirlo así terminan siendo unas
grandes figuras determinadas fractales.