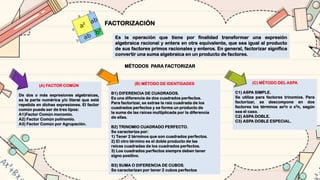
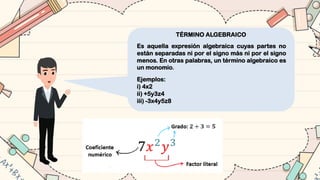
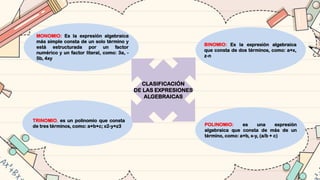
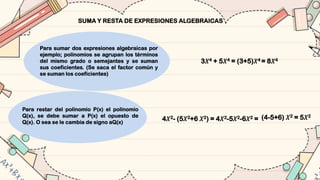
El documento ofrece una introducción al álgebra, definiendo conceptos fundamentales como expresiones algebraicas, términos algebraicos, y la clasificación de estas expresiones. Se detallan las operaciones básicas de suma, resta, multiplicación y división de polinomios, así como propiedades y métodos para la factorización de expresiones algebraicas. Además, se incluyen ejemplos de ejercicios y productos notables que ilustran la aplicación de las teorías algebraicas.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN UNIVERSITARIA
UNIVERSIDAD POLITÉCNICA TERRITORIAL ANDRES ELOY BLANCO
ESTADO LARA
Br. Roxanna Doroteo, C.I: 29707003
Br. Mariana Molina, C.I: 30621067
Br. Zulanny Pastran, C.I: 25136726
Br. Dilan Briceño, C.I: 30759490
Br. Jose Domoromo, C.I: 25340076

2. Qué es
Álgebra?
Es la rama de la matemática que
estudia las operaciones entre
cantidades literales, así como las
propiedades que rigen estas
operaciones.
Parte de la matemática que estudia a
la cantidad en su forma más general
obteniendo generalizaciones sobre el
comportamiento operacional de los
números.

3. EXPRESIÓN ALGEBRAICA
Es el conjunto de números y letras unidos entre sí
por los signos de operación de la suma, la resta, la
multiplicación, la división, la potenciación y la
radicación.
EJEMPLOS:
Son expresiones algebraicas las siguientes:
i) x
ii) 4x
iii) 4x2 + 5y2 + 7z2
_________
iv) 3x5 + 7 √ x2 - 5xy4
________________
3x2y - 3xy7
No son expresiones algebraicas:
i) 5x
ii) log x
iii) sen x

4. TÉRMINO ALGEBRAICO
Es aquella expresión algebraica cuyas partes no
están separadas ni por el signo más ni por el signo
menos. En otras palabras, un término algebraico es
un monomio.
Ejemplos:
i) 4x2
ii) +5y3z4
iii) -3x4y5z8

5. CLASIFICACIÓN
DE LAS EXPRESIONES
ALGEBRAICAS
MONOMIO: Es la expresión algebraica
más simple consta de un solo término y
está estructurada por un factor
numérico y un factor literal, como: 3a, -
5b, 4xy
BINOMIO: Es la expresión algebraica
que consta de dos términos, como: a+x,
z-n
TRINOMIO. es un polinomio que consta
de tres términos, como: a+b+c; x2-y+z3 POLINOMIO: es una expresión
algebraica que consta de más de un
término, como: a+b, x-y, (a/b + c)

6. Ejercicio Nº 8.-
En cada una de estas expresiones, razona si se trata de un polinomio, de una
identidad o de una ecuación:
a) 2 (X +1) = 2X + 2
b) 2 (X+1)= 8
c) 2X + 2
d) X4 – 3X2 + 5X – 1 = 0
RESPUESTA:
1. En lo que concierne a la letra a, es una ecuación.
2. En lo que concierne a la letra b, es una ecuación.
3. Con respecto a la letra c es un polinomio.
4. Con respecto a la letra de es una ecuación.

7. SUMA Y RESTA DE EXPRESIONES ALGEBRAICAS
Para sumar dos expresiones algebraicas por
ejemplo; polinomios se agrupan los términos
del mismo grado o semejantes y se suman
sus coeficientes. (Se saca el factor común y
se suman los coeficientes)
3𝑋4 + 5𝑋4 = (3+5)𝑋4 = 8𝑋4
Para restar del polinomio P(x) el polinomio
Q(x), se debe sumar a P(x) el opuesto de
Q(x). O sea se le cambia de signo aQ(x)
4𝑋2- (5𝑋2+6 𝑋2) = 4𝑋2-5𝑋2-6𝑋2 = (4-5+6) 𝑋2 = 5𝑋2

8. Ejercicio Nº 11.-
Dados los polinomios A = -3X2 + 2X – 1 y B= X2 + 3X + 1, calcula:
a) 2A – B
b) A * B
Respuesta del ejercicio a
2 (-3X2 + 2X – 1) -6X2 + 4X - 2
X2 + 3X + 1 -X2 - 3X - 1
Resultado: -7X2 + X - 3
Respuesta del ejercicio b
-3X2 + 2X – 1
X2 + 3X + 1_
-3X4 + 2X3 – X2
- 9X3 + 6 X2 -3X
- 3X2 + 2X – 1
-3X4 – 7X3 +2X2 –X -1 Resultado
Para restar multiplicamos por menos el
polinomio sustraendo cambiando el signo a
todos los términos, y lo colocamos debajo del
otro polinomio, cuidando que estén alineados
los términos semejantes.

9. MULTIPLICACIÓN DE EXPRESIONES ALGEBRAICAS
Es la operación que consiste en
obtener una expresión llamada
producto total, conociendo
otras dos llamadas
multiplicando y multiplicador.
PROPIEDADES DE LA MULTIPLICACIÓN
1) El grado del producto es igual a la suma de los
grados de los factores.
2) El término independiente del producto es igual al
producto de los términos independientes de los
factores.
CASOS QUE SE PRESENTAN EN LA MULTIPLICACIÓN
I) CUANDO SON DOS MONOMIOS.
Se multiplica los signos, luego los coeficientes y por último las
partes literales utilizando la teoría de los exponentes.
II) CUANDO SON DOS POLINOMIOS.
En este caso se puede utilizar dos métodos.
a) MÉTODO NORMAL.- Se ordenan los polinomios preferentemente
en forma descendente y se escriben uno debajo del otro. A
continuación se multiplica separadamente cada término del
multiplicador, por cada uno de los términos del multiplicando,
sus signos, sus coeficientes y sus letras; y se obtiene los
productos parciales, los cuales se escriben en forma ordenada
uno debajo del otro del mismo grado y se suma ordenadamente
obteniéndose el producto total.
b) MÉTODO DE COEFICIENTES SEPARADOS.-
1) Los polinomios deben estar ordenados descendentemente.
2) Se escriben los coeficientes del multiplicando, y multiplicador en
línea horizontal, uno debajo del otro.
3) Se opera como en el método anterior, corriendo un lugar hacia la
derecha después de obtener cada producto parcial.
4) Para obtener el grado del producto total se aplica la propiedad
del grado del producto.

10. EJEMPLO A
Efectuar:
(4x3 + 5x2 y + 7xy2 - 2y3) (2x2 - 5xy + 3y2 )
Solución:
Disposición de la operación:
4x3 + 5x2y + 7xy2 - 2y3
2x2 - 5xy + 3y2
––––––––––––––––––––––––––––––
8x5 + 10x4y + 14x3y2 - 4y2x3
-20x4y - 25x3y2 - 35x2y3 + 10xy4
+12x3y2 + 15x2y3 + 21xy4 - 6y5
––––––––––––––––––––––––––––––––––––––––––
8x5 - 10x4y + x3y2 - 24x2y3 + 31xy4 - 6y5
EJEMPLO B
Efectuar:
(4x3 + 7x2 - 6) (2x2 - 3x - 4)
Solución:
La operación se dispone de la siguiente manera:
4 + 7 + 0 - 6
2 - 3 - 4
–––––––––––––––––––––––
8 + 14 + 0 - 12
- 12 - 21 - 0 + 18
- 16 - 28 - 0 + 24
––––––––––––––––––––––––––––––––––––––
8 + 2 - 37 - 40 + 18 + 24
El grado del producto es:
3 + 2 = 5
El producto total es:
8x5 + 2x4 - 37x3 - 40x2 + 18x + 24

11. DIVISIÓN DE EXPRESIONES ALGEBRAICAS
Operación que consiste en obtener una expresión llamada
cociente, conocidas otras dos, llamadas dividendo y divisor.
CASOS DE LA DIVISIÓN
I.- CUANDO SE TRATA DE DOS
MONOMIOS.
a) Se divide los signos mediante la regla
de los signos.
b) Se divide los coeficientes.
c) Se divide las letras aplicando Teoría de
exponentes.
II.- CUANDO SE TRATA DE DOS POLINOMIOS.
Se puede utilizar cualquiera de los siguientes
métodos:
a) Método normal
b) Método de coeficientes separados.
c) Método de Horner.
d) Método de Ruffini.

12. PRODUCTOS NOTABLES
Denominados también “identidades algebraicas”. Son
aquellos productos cuyo desarrollo es clásico y por esto se le
reconoce fácilmente. Los más importantes son:
I) CUADRADO DE UNA SUMA
Y UNA DIFERENCIA.
• (a + b)2 = a2 + 2ab + b2
• (a - b)2 = a2 - 2ab + b2
En general
(a ± b)2 = a2 ± 2ab + b2
II) PRODUCTO DE UNA SUMA POR SU DIFERENCIA.
Es igual a la diferencia de cuadrados:
(a + b)(a - b) = a2 - b2
III) CUADRADO DE UN TRINOMIO.
(a + b + c)2 = a2 +b2 + c2 + 2ab + 2ac + 2bc
IV) CUBO DE UNA SUMA O
DIFERENCIA.
• (a + b)3 = a3 + 3a2b + 3ab2 + b3
• (a - b)3 = a3 - 3a2b + 3ab2+b3
(a ± b)3 = a3 ± 3a2b + 3ab2 ± b3
V) PRODUCTO DE DOS BINOMIOS QUE TIENEN
UN TÉRMINO COMÚN.
(x + a) (x + b) = x2 + (a + b)x + ab
VI) PRODUCTO DE UN BINOMIO POR UN
TRINOMIO QUE DA UNA SUMA O DIFERENCIA DE
CUBOS.
• (a + b) (a2 - ab + b2) = a3 + b3
• (a - b) (a2 + ab + b2) = a3 - b3
De manera general:
(a ± b) (a2 ab + b2) = a3 ± b3
VII) IDENTIDADES DE LEGENDRE
• (a + b)2 + (a - b)2 = 2(a2 + b2)
• (a + b)2 - (a - b)2 = 4ab
VIII) IDENTIDADES DE LAGRANGE
• (ax + by)2 + (bx - ay)2 = (x2 + y2)(a2 + b2)

13. EJEMPLO
Efectuar:
R = (a + b + c)(a + b - c)+(a + b - c)(a -b + c)
+(a - b + c)(b + c - a)+ (b - c + a)(b - c - a) - 4ab
Solución:
Reescribiendo la expresión de la manera siguiente:
R = [(a + b) + c][(a + b) - c] + [a + (b - c)]
[a - (b - c)] + [c + (a - b)][c - (a - b)]
+[(b - c) + a][(b - c) - a] - 4ab
Efectuando los productos notables:
R = (a + b)2 - c2 + a2 -(b - c)2 + c2 - (a - b)2
+ (b - c)2 - a2 - 4ab
Reduciendo términos semejantes se obtiene:
R = (a + b)2 - (a - b) - 4ab
R = 4ab - 4ab = 0
Respuesta. R = 0

14. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
Es el valor que toma dicha expresión cuando se le atribuye
ciertos valores numéricos a sus letras. Puede ser:
A) VALOR NUMÉRICO SIN CONDICIÓN.
Es aquel que se obtiene al reemplazar
inmediatamente los valores atribuidos a sus
letras.
Ejemplo: Hallar el valor de:
E =√(a - y) (√2bx + x) + √(a - x)(b + y)
para a = 16; b = 10 ; x = 5 ; y = 1
Solución:
Reemplazando los valores asignados:
E =√(16 - 1)(√2(10)(5) + 5)+ √(16 - 5)(10 + 1)
E = √15(10 + 5) + √11 . 11
E = 15 + 11 = 26
Respuesta.: E = 26
B) VALOR NUMÉRICO CON CONDICIÓN.
Es aquel que se caracteriza porque utiliza
una condición de intermedio. Para
determinarlo se emplea la condición
simplificándola y luego aplicándola con la
expresión misma y luego cambiándola con
la condición.

15. FACTORIZACIÓN
Es la operación que tiene por finalidad transformar una expresión
algebraica racional y entera en otra equivalente, que sea igual al producto
de sus factores primos racionales y enteros. En general, factorizar significa
convertir una suma algebraica en un producto de factores.
MÉTODOS PARA FACTORIZAR
(A) FACTOR COMÚN
De dos o más expresiones algebraicas,
es la parte numérica y/o literal que esté
repetida en dichas expresiones. El factor
común puede ser de tres tipos:
A1)Factor Común monomio.
A2) Factor Común polinomio.
A3) Factor Común por Agrupación.
(B) MÉTODO DE IDENTIDADES
B1) DIFERENCIA DE CUADRADOS.
Es una diferencia de dos cuadrados perfectos.
Para factorizar, se extrae la raíz cuadrada de los
cuadrados perfectos y se forma un producto de
la suma de las raíces multiplicada por la diferencia
de ellas.
B2) TRINOMIO CUADRADO PERFECTO.
Se caracteriza por:
1) Tener 2 términos que son cuadrados perfectos.
2) El otro término es el doble producto de las
raíces cuadradas de los cuadrados perfectos.
3) Los cuadrados perfectos siempre deben tener
signo positivo.
B3) SUMA O DIFERENCIA DE CUBOS.
Se caracterizan por tener 2 cubos perfectos
(C) MÉTODO DEL ASPA
C1) ASPA SIMPLE.
Se utiliza para factores trinomios. Para
factorizar, se descompone en dos
factores los términos ax2n o x2n, según
sea el caso.
C2) ASPA DOBLE.
C3) ASPA DOBLE ESPECIAL.

17. REFERENCIAS
Aufmann, R. y Lockwood, J. (2013). Álgebra
Elemental. 8va. Edición. Cengage Learning. México.
Baldor, A. (s/f). Álgebra.
Lexus Editores S.A. (2008). Álgebra: Manual de
preparación preuniversitaria.