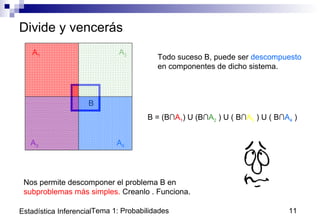
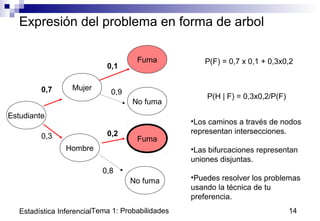
Este documento presenta conceptos básicos sobre probabilidad en el Tema 1 del curso de Estadística Inferencial. Introduce las nociones de suceso, espacio muestral y probabilidad, así como reglas para calcular probabilidades como la probabilidad total y la probabilidad condicional. Explica el uso de sistemas exhaustivos y excluyentes de sucesos y la regla de Bayes para resolver problemas de probabilidad. Por último, aplica estos conceptos al análisis de pruebas diagnósticas médicas.