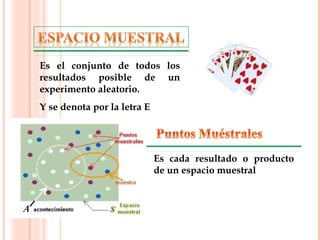
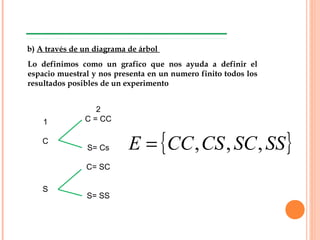
El documento describe la importancia de los modelos matemáticos en el estudio de fenómenos físicos, sociales y económicos, y distingue entre modelos determinísticos y probabilísticos. Se abordan conceptos fundamentales de la teoría de probabilidad, incluyendo la definición de eventos, espacios muestrales y axiomas básicos, así como la diferencia entre eventos independientes y dependientes. Además, se presentan teoremas relacionados con la adición y multiplicación de probabilidades en contextos de eventos mutuamente excluyentes y no excluyentes.

1. UNIVERSIDAD CENTROCCIDENTAL
“LISANDRO ALVARADO”
DECANATO DE AGRONOMIA
NUCLEO “DR. ARGIMIRO BRACAMONTE”
Prof. : Enely Freitez
Enero, 2015

3. Es una representación simbólica de un fenómeno
cualquiera, realizado con el fin de estudiarlo mejor.
Ejemplo: Fenómenos físicos, económicos, sociales, etc.
Los modelos matemáticos pueden ser:
-Modelos Determinísticos
-Modelos Probabilísticos

4. Cuando se realiza un modelo matemático de un
fenómeno y en el se pueden manejar los factores que
intervienen en su estudio con el propósito de predecir
sus resultados.
Ejemplo:
El modelo de una compañía en donde dos
productos se elaboran al pasar en forma
sucesiva por tres maquinas. Ahí el tiempo
por maquina asignado a los dos productos
está limitado por una cantidad de horas
por días. Igualmente el tiempo de
producción y la ganancia de cada producto
se puede establecer de tal manera que
combinando los productos podemos
obtener una ganancia optima

5. A los modelos matemáticos de los fenómenos en cuales
no se puede controlar los factores que intervienen en
un estudio, y además dichos factores ocurren de tal
manera que no se pueden predecir sus resultados.
Ejemplo:
Si deseamos conocer el lugar de caída de un
satélite, que se salió de su orbita y se dirige
a la tierra, no podemos predecir el lugar
donde el caerá puesto que no podemos
controlar sus movimientos, por lo tanto
solo es posible indicar una región en donde
se cree que caerá el satélite con un valor
numérico que represente la evaluación

6. Matemáticamente se define como sigue:
La probabilidad p de un evento A es:
Si A puede ocurrir de entre un total de N
igualmente probables, entonces se cumple:
Es decir, si un experimento que está sujeto al azar,
resulta de n formas igualmente probables y
mutuamente excluyentes, y si una parte de estos n
resultados tienen un atributo A, la probabilidad de A
es la proporción de las veces que ocurre A con respecto
a n. Los resultados se establecen a priori
AN
N
N
AP A
=)(

7. La probabilidad relativa de un evento A es la
proporción de las veces en que ocurriría a la larga
eventos del mismo tipo. Se define como sigue:
N
N
AP A
N
Lim∞→
=)(
La interpretación de una frecuencia relativa descansa en la idea
de que un experimento se efectúa y se repite muchas veces bajo las
mismas condiciones. Cada vez que un experimento se lleva a cabo,
se observa un resultado, este es impredecible dada la naturaleza
aleatoria del experimento. La probabilidad de la presencia de
cierto atributo se aproxima por la frecuencia relativa de los
resultados que posee dicho atributo. Conforme aumenta la
repetición del experimento, la frecuencia relativa de los resultados
favorables se aproxima al verdadero valor de la probabilidad para
ese atributo

8. La probabilidad de un evento se cuantifica asignándole un
numero del intervalo ; o el porcentaje del 0 al 100%, es
decir
- Un cero indica que el resultado no se presentará.
- Un 1 indica un resultado seguro.
[ ]1,0
En otras palabras, podemos decir:
Algo poco probable es algo que se espera y le
corresponde un numero pequeño como
probabilidad, mientras que un suceso altamente
probable es aquel que se considera muy viable y
en consecuencia le corresponde una
probabilidad muy cercana a 1

9. Un experimento aleatorio es aquel en el cual se
desconoce su resultado, pues está sujeto al azar, y
además se puede repetir indefinidamente sin
cambiar esencialmente las condiciones.
En otras palabras es el proceso por el cual se
describen los resultados y no se pueden predecir.
Ejemplo:
EXPERIMENTO RESULTADOS POSIBLES
Lanzamiento de una moneda Cara, sello
Lanzamiento de un dado 1, 2, 3, 4, 5, 6
Seleccionar un tornillo de cierta
producción
Defectuoso, no defectuoso
Vamos a estudiar algunos conceptos fundamentales de la teoría
de probabilidad.

10. 1- Cada experimento tiene varios resultados
posibles que se especifican de antemano.
2 – No tenemos la certeza del resultado de cada
experimento

11. Es el conjunto de todos los
resultados posible de un
experimento aleatorio.
Y se denota por la letra E
Es cada resultado o producto
de un espacio muestral

12. Lanzar un dado y observar el
numero que sale en la cara
superior
{ }6,5,4,3,2,1=E
{ }3=T

13. Lanzar una moneda
{ }sellocaraE ,=

14. Lanzar simultáneamente dos
moneda

15. a) Por medio de un producto cartesiano:
Tomando cada resultado de la primera
moneda y combinándolo con todos los
resultados de las otras monedas
Primera Moneda lanzada Segunda Moneda
lanzada
C S
C CC CS
S SC SS
{ }SSSCCSCCE ,,,=
Así, el espacio muestral sería:

16. Lo definimos como un grafico que nos ayuda a definir el
espacio muestral y nos presenta en un numero finito todos los
resultados posibles de un experimento
b) A través de un diagrama de árbol
1
C
S
2
C = CC
S= Cs
C= SC
S= SS
{ }SSSCCSCCE ,,,=

17. Dado un experimento aleatorio y su
espacio muestral E, se llama evento a
un conjunto de resultados posibles de
E, es decir que un evento no es más
que un subconjunto de un espacio
muestral
Ejemplo:
Si lanzamos un dado y observamos el
numero que sale en la cara superior,
entonces:
Sea B el evento: Sale un numero par
{ }6,5,4,3,2,1=E
{ }6,4,2=B

18. Evento que consta de un
solo elemento.
Son aquellos que se forman
a partir de dos o mas
eventos simples tomando en
cuenta las operaciones entre
conjuntos.

19. Sea el experimento lanzar un dado y observamos el numero
que sale en la cara superior, es decir: { }6,5,4,3,2,1=E
Sean algunos eventos simples del experimento
A = {Sale un número par}= {2, 4, 6}
B = {Sale un número impar}= {1, 3, 5}
C = {Sale un número primo}= {2, 3, 5}
Definamos algunos eventos compuestos:
A C= {Sale un número par o primo} = {2, 4, 6,3,5}
A B = {Sale un número impar primo}= {3,5}
C’ = {Que el número no sea primo}= {1, 4, 6}



20. Dado un experimento aleatorio, con espacio
muestral E, con resultados posibles mutuamente
excluyentes tal que cumplen con
las leyes del algebra de eventos. Se cumplen los
siguientes axiomas:
a)Axioma 1 (Axioma de positividad)
La probabilidad de todo evento o suceso es
un número, es decir
nxxx ,,........., 21
0)( ≥ixP

21. b) Axioma 2 (Axioma de Certidumbre)
La suma de las probabilidades de todos
los sucesos posibles mutuamente excluyentes de
un experimento aleatorio es la unidad. Esto es:
Claro está, como la suma de todos los sucesos
mutuamente excluyentes es el espacio muestral,
la expresión anterior la podemos escribir como:
1)(..........)()( 21 =+++ nxPxPxP
1)( =SP

22. c) Axioma 3
Si es un evento cualquiera de un espacio
muestral, se cumple:
1)(0 ≤≤ EP
E
c) Axioma 4 (Axioma de Uniones)
Si para los eventos se tiene que
Entonces:
)(..........)()()....( 2121 nn EPEPEPEEEP +++=∪∪∪
nEEE ,....,, 21
jiEE ji ≠∀=∩ ;φ

23. Como consecuencia inmediata de los axiomas
anteriores, se deducen las siguientes propiedades de
eventos
a) Teorema 1
Sea Ф el evento vacío, entonces
b) Teorema 2
Si A es un evento y A’ su complemento, entonces
c) Teorema 3
Para cualquier evento A,
d) Teorema 4
Si A y B son dos eventos de un mismo espacio
muestral, tales que , entonces
0)( =φP
)(1)'( APAP −=
1)(0 ≤≤ AP
BA ⊂ )()( BPAP ≤

24. Teorema 5 (Teorema de la Adición)
Este teorema de la adición se aplica a los siguientes
tipos de eventos:
)()()( BPAPBAP +=∪
a) Eventos Mutuamente
Excluyentes
Sea S un espacio muestral que
contiene a cualesquiera dos
eventos A y B (A y B son
disjuntos), entonces se cumple:

25. Sea S un espacio muestral que
contiene a cualesquiera dos
eventos A y B (A y B son no
disjuntos), entonces se cumple:
)()()()( BAPBPAPBAP ∩−+=∪
)()()()()( CBAPCPBPAPCBAP ∩∩−++=∪∪
b) Eventos No Mutuamente Excluyentes
Puede generalizarse para tres o más eventos, es
decir:

26. Sea S un espacio muestral que contiene a cualesquiera
dos eventos A y B con . La probabilidad
condicional de B dado A está definida como sigue:
La probabilidad de un evento B dado otro A, es la
probabilidad de que el evento B ocurre cuando
sabemos que el evento A ocurrió, es decir, la
probabilidad de B está condicionada por la
ocurrencia de A
)(
)(
)/(
AP
BAP
ABP
∩
=
0)( >AP

27. Como consecuencia inmediata de la probabilidad
condicional surge el teorema de la multiplicación
Sea S un espacio muestral que
contiene a cualesquiera dos eventos
A y B con . Entonces:0)( >AP
)/().()( ABPAPBAP =∩
Este teorema se puede generalizar, y se tiene:
Con
)/()./().()( BACPABPAPCBAP ∩=∩∩
0)( >∩ BAP

28. ; Con P(A)>0 y P(B)>0)().()( BPAPBAP =∩
A y B son independientes si el suceso A no depende
del suceso B y B no depende de A, es decir, cuando la
ocurrencia de uno no influye sobre la probabilidad
de ocurrencia del otro. Y se define:
El concepto de independencia puede extenderse a
tres o más eventos
Eventos Independientes
Esta definición también recibe el nombre de la
Regla de Multiplicación con remplazo

29. ; Con P(A)>0 y P(B)>0)/().()( ABPAPBAP =∩
Dos sucesos A y B son dependientes si la ocurrencia
de un suceso afecta la probabilidad de ocurrencia del
otro suceso, es decir, los sucesos están relacionados.
Y se determina como sigue:
Eventos Dependientes
Esta definición también recibe el nombre de la
Regla de Multiplicación sin remplazo

30. ARMAS, J. Estadística Sencilla, Teoría de Probabilidad.
Universidad de los Andes. Facultad de Ciencias Económicas y
Sociales. Dpto. de Estadística Mérida (1996).
MONTGOMERY, D. Control Estadístico de la Calidad. Editorial
Iberoamericana. México. (1991).
ORTEGA, J. Elementos de Probabilidad. Editorial CENAMEC.
Caracas – Venezuela (1998)