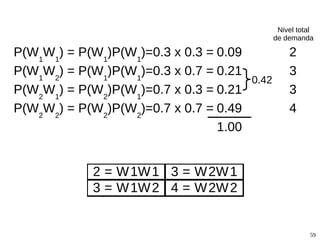
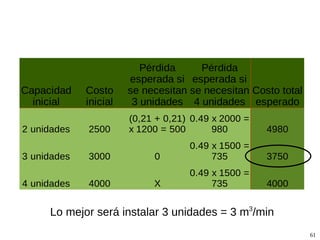
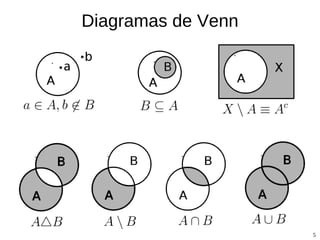
El documento proporciona una introducción a la teoría de probabilidades, abordando conceptos fundamentales como fenómenos aleatorios, definiciones de probabilidad y sus interpretaciones frecuentista y bayesiana. Se explora el espacio muestral, eventos, axiomas de Kolmogorov, y técnicas de conteo, además de discutir eventos independientes y los teoremas de probabilidades totales y de Bayes. También se presentan ejemplos prácticos y aplicaciones en diversos contextos, incluidos experimentos de laboratorio y situaciones cotidianas.

1. 02 - Introducción a la teoría de probabilidad Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales

2. Contenido Repaso de teoría de conjuntos Fenómenos determinísticos vs. fenómenos aleatorios Definición de probabilidad Interpretación frecuentista y Bayesiana de la probabilidad Espacio muestral, eventos Sigma-álgebra Medida de probabilidad, definición, propiedades Axiomas de Kolmogorov Probabilidad conjunta, marginal, condicional Eventos independientes Teorema de las probabilidades totales, teorema de Bayes Técnicas de conteo: factorial, permutación, combinatoria

3. Repaso de la teoría de conjuntos

4. Operaciones con conjuntos

5. Diagramas de Venn

6. Propiedades

9. Conjunto potencia (power set)

10. Ejemplos de teoría de conjuntos

11. Teoría de la probabilidad La teoría de la probabilidad es la teoría matemática que modela los fenómenos aleatorios . Un fenómeno (o experimento) aleatorio es aquel que, a pesar de realizarse el experimento bajo las mismas condiciones determinadas, tiene como resultados posibles un conjunto de alternativas (el llamado espacio muestral ), como el lanzamiento de un dado o de una moneda. Estos deben contraponerse a los fenómenos determinísticos , en los cuales el resultado de un experimento, realizado bajo condiciones determinadas, produce un resultado único o previsible: por ejemplo, el agua calentada a 100 grados Celsius, a nivel del mar, se transforma en vapor.

12. Probabilidad La probabilidad es una forma de expresar el conocimiento o la creencia que un evento ha ocurrido o va a ocurrir. Existen dos formas de interpretar la probabilidad: Interpretación frecuentista Interpretación Bayesiana La comunidad científica está dividida entre personas que apoyan una interpretación o la otra.

13. Interpretación frecuentista de probabilidad Los frecuentistas hablan sobre probabilidades solo cuando se trata de experimentos que son aleatorios y están bien definidos. La probabilidad de un evento se refiere a la frecuencia relativa de ocurrencia del resultado de un experimento aleatorio.

14. De este modo para un frecuentista, la definición de probabilidad sería: Definición: si un experimento que está sujeto al azar resulta de n formas igualmente probables y mutuamente excluyentes (es decir que ocurren bajo las mismas condiciones), y su n A de estos resultados tienen un atributo A , la probabilidad del atributo A es: Interpretación frecuentista de probabilidad

15. Interpretación Bayesiana de probabilidad Los Bayesianos utilizan la probabilidad como un medio subjetivo para representar el grado de creencia en una afirmación, dada la evidencia. Ellos asignan probabilidades a cualquier afirmación, incluso cuando no hay un experimento aleatorio involucrado. Ejemplo: la probabilidad que el Once Caldas gane el próximo partido es del 80% (o la probabilidad que pierda o empate es del 20%). Esto quiere decir que una apuesta justa sería 8 a 2 a que el Once ganaría. Ganancia = -8 x 0.2 + 2 x 0.8 = 0

16. Nota 1: A veces el futuro no se puede predecir y solo se puede calcular la probabilidad de que algo suceda. Nota 2: En el lanzamiento de un dado los resultados son mutuamente excluyentes y mutuamente probables. La probabilidad de obtener un 4 es 1/6. Esto no significa que en 6 tiradas tengamos necesariamente que obtener un 4. Nota 3: El desarrollo inicial de la teoría de probabilidades se asocia al estudio de los juegos de azar.

17. Espacio muestral Ω Es el conjunto de todos los posibles resultados de un experimento aleatorio. Los elementos ω del conjunto Ω se denominan puntos muestrales. Un evento (o suceso ) del espacio muestral es un subconjunto de Ω cuyos miembros tienen una característica común.

18. El espacio muestral Ω puede ser Discreto (cardinalidad finita o infinita contable: los resultados pueden ponerse uno a uno con los números naturales) Continuo (cardinalidad infinita no contable: los resultados consisten de intervalos de los números reales)

19. Espacio muestral discreto Las caras de un dado forman el espacio muestral Cada uno de los cuatro bits transmitidos se clasifica como con error o sin error. s = sin error, c = con error

20. Las especificaciones de un computador pueden especificarse en 1, 2 o 4 Gb de memoria y en 200, 300 o 400 Gb de disco duro, tienen el espacio muestral: Ω = {(1,200); (2,200); (4,200); (1,300); (2,300); (4,300); (1,400); (2,400); (4,400)} El número de lanzamientos de una moneda hasta obtener caras tiene el espacio muestral Ω = {1, 2, 3, 4, ..., ∞ }

22. Espacio muestral continuo El espacio muestral que representa la altura de una persona se puede especificar por el espacio muestral Ω = [0, 3] metros. El espacio muestral que representa el tiempo que se debe esperar la buseta se puede especificar por el espacio muestral Ω = [0, ∞ ) minutos.

23. Eventos El espacio muestral Ω es un evento que se le llama el evento seguro El conjunto vacío Ø es un evento llamado el evento imposible Sean dos eventos A y B, si ambos son conjuntos disjuntos, entonces ellos son eventos mutuamente excluyentes . A una colección de eventos A 1, A 2 , A 3 ... (sea finita o infinita contable) se le conoce como eventos exhaustivos si su unión es el espacio muestral Ω.

24. Espacio muestral en experimentos con reemplazo y sin reemplazo

25. Diagrama del árbol

26. Sigma-algebra: motivación Cuando analizamos eventos aleatorios, generalmente no estamos interesados en Ω sino en un subconjunto E ∈ Ω. Cuando analizamos las probabilidades de ocurrencia del evento E, tambien nos interesan las probabilidades de la no ocurrencia del evento E. Además si nos interesa la probabilidad de ocurrencia de los eventos A 1 y A 2 también nos interesaría la probabilidad de su unión.

27. Sigma-álgebra

28. Ejemplos

29. Algunas definiciones Un par ordenado (X, σ X ), donde X es un conjunto y σ X una σ-álgebra sobre éste, se denomina espacio medible . Una función entre dos espacios medibles se denomina función medible si la preimagen de todo conjunto medible es también medible; esto es, si (X, σ X ) y (Y, σ Y ) son dos espacios medibles, una función f:X->Y es medible si para todo E ∈ σ Y , f −1 (E) ∈ σ X . Una medida es una cierta clase de función que mapea puntos de una σ-álgebra al intervalo [0,∞).

30. Andrey Nikolaevich Kolmogorov (Abril 25, 1903 – Octubre 20, 1987)

31. Axiomas de probabilidad de Kolmogorov

32. Axiomas de probabilidad de Kolmogorov

33. Consecuencias de los tres axiomas de probabilidad

34. Consecuencias de los tres axiomas de probabilidad

35. Consecuencias de los tres axiomas de probabilidad

36. Consecuencias de los tres axiomas de probabilidad

37. Ejemplos

39. Probabilidad conjunta Cual es la probabilidad de ser mujer fumadora?

40. Probabilidad marginal Cual es la probabilidad de ser fumador? Suma sobre todos los j Suma sobre todos los i

41. Probabilidad condicional Cual es la probabilidad de ser fumador dado que se es mujer? Probabilidad condicional de A i dada la ocurrencia de B j

42. Probabilidad condicional Cual es la probabilidad de ser mujer dado que se es fumador? Probabilidad condicional de B j dada la ocurrencia de A i

43. Diagrama del árbol

44. En general, tenemos la regla de la multiplicación: Para definir las probabilidades conjuntas, marginales y condicionales se ha empleado un ejemplo específico en el que el espacio muestral contiene un número finito de resultados. Sin embargo, las definiciones dadas aquí son completamente generales y pueden extenderse para cualquier espacio muestral, ya sea discreto o continuo.

45. Ejemplo En una encuesta de televisión se determina que al 20% de las personas les gusta el programa A, al 16% de las personas les gusta el programa B y al 1% de les gusta ambos programas. Si se selecciona al azar un televidente de B( A ), cual es la probabilidad que también le guste A( B )?

46. La paradoja del falso positivo

51. Propiedades de la probabilidad condicional

52. Ejemplos

53. Probabilidad condicional con varias variables aleatorias

54. Ejemplo Una bolsa tiene 10 bolas blancas y 30 rojas. ¿Cuál es la probabilidad de muestrear BBRB? Muestreo sin reemplazo Muestreo con reemplazo

55. Ejemplo

56. Arboles de decisión

57. Ejemplo

59. Ejemplo Una pareja planifica utilizando DemoProvera (confiabilidad = 99.7%/año) y condón de latex masculino (confiabilidad = 98%/año) simultáneamente. Si la probabilidad de quedar en embarazo al tener relaciones sin protección es del 85%/año, ¿cuál es la probabilidad de un embarazo no deseado? Porcentajes sacados de: http://en.wikipedia.org/wiki/Comparison_of_birth_control_methods

60. Eventos independientes

61. Eventos independientes Esto quiere decir que si la ocurrencia de B no tiene ningún efecto sobre la probabilidad de A, entonces se tiene que P(A|B)=P(A), a pesar que ha ocurrido el evento B. Dentro de la teoría matemática, sólo podemos probar la independencia de eventos obteniendo P(A), P(B) y P(A ∩ B) y demostrando que se verifica una de las ecuaciones anteriores marcadas en el recuadro. En la práctica de ingeniería, normalmente se confía en el conocimiento de la situación física para afirmar que en el modelo dos eventos particulares se supondrán (o no) independientes.

62. Ejemplo

63. Ejemplo Suponga que se quiere diseñar el acueducto de un parque industrial que tendrá dos fábricas. Supongamos que existen dos niveles de demanda de agua: W 1 = 1 m 3 /min y W 2 = 2 m 3 /min. La probabilidad que cualquier fábrica requiera dichos niveles de demanda son 0.3 y 0.7 respectivamente (P(W 1 )=0.3, P(W 2 )=0.7). Dichos niveles de demanda de ambas fábricas son estádísticamente independientes. ¿Cuál es la combinación de niveles de demanda menos probable? más probable? Fabrica 1 Fabrica 2

64. P(W 1 W 1 ) = P(W 1 )P(W 1 )=0.3 x 0.3 = 0.09 2 P(W 1 W 2 ) = P(W 1 )P(W 1 )=0.3 x 0.7 = 0.21 3 P(W 2 W 1 ) = P(W 2 )P(W 1 )=0.7 x 0.3 = 0.21 3 P(W 2 W 2 ) = P(W 2 )P(W 2 )=0.7 x 0.7 = 0.49 4 1.00 Nivel total de demanda 0.42

65. Si los costos de instalación inicial y de ensanche son los siguientes: Costos de instalación inicial: Dos unidades = $2500 Tres unidades = $3000 Cuatro unidades = $4000 Costo de ensanche: Dos a tres unidades = $1200 Tres a cuatro unidades = $1500 Dos a cuatro unidades = $2000 Que capacidad inicial instalaría usted de modo que el costo total esperado del proyecto sea el mínimo?

66. Lo mejor será instalar 3 unidades = 3 m 3 /min

67. Regla de la multiplicación para eventos independientes

68. Ejemplo

70. Condere una red de acueducto. En el gráfico se muestra la configuración de la misma junto con la posición de las bombas A, B, C y D. Dado que la probabilidad de falla de dichas bombas es 0.2, 0.3, 0.1 y 0.05 respectivamente, calcule la probabilidad con la que el agua puede efectivamente transportarse desde el punto 1 hasta el punto 2. Tenga en cuenta que:

74. serie paralelo

75. Propiedad de Markov P(A|B,C) = P(A|B) independientemente de la ocurrencia de C Ver http://en.wikipedia.org/wiki/Markov_chain http://en.wikipedia.org/wiki/Examples_of_Markov_chains http://en.wikipedia.org/wiki/Markov_property

76. Relación entre eventos independientes y eventos mutuamente excluyentes

77. Teorema de las probabilidades totales

78. Para un chip se sabe que:

79. Thomas Bayes (aprox. 1702 – Abril 7, 1761) Essay Towards Solving a Problem in the Doctrine of Chances (1764)

80. Teorema de Bayes

82. Ejercicio Suponga que tenemos dos urnas: A y B. Las cuales se muestran en la figura. En A hay siete bolas rojas (red - R) y tres bolas blancas (white - W). En B hay una bola roja y nueve blancas. Se lanza una moneda. Si caen caras se saca una bola de la urna A y si cae en sellos se saca una bola de la urna B. Si se lanzó la moneda y se sacó una bola roja, cual es la probabilidad que esta bola provenga de la urna A?

84. Redes bayesianas

85. Ejercicios

86. Conteo de datos con la ayuda del factorial Para calcular las probabilidades de varios eventos es necesario contar el número de resultados posibles de un experimento o contar el número de resultados que son favorables a un evento dado. El proceso de conteo puede simplificarse mediante el empleo de dos técnicas de conteo denominadas permutaciones y combinaciones .

87. Factorial

88. Factorial

89. Factorial en MS EXCEL Se calcula utilizando la función FACT

90. Factorial en MATLAB FACTORIAL(N): como los números de doble precision solo almacenan 15 dígitos, la respuesta es exacta para N ≤ 21. Si N>21, la respuesta solo será aproximada.

91. La función gamma La función gamma en MS EXCEL y en MATLAB

92. Es el número de arreglos en un orden en particular de los elementos que forman un conjunto. De cuantas formas diferentes se pueden ubicar a, b y c? a b c a c b b a c b c a c a b c b a Permutación P(n,r) Para la primera posición se escoje cualquiera de las letras Para la segunda posición se puede escoger dos letras para la primera posición Para la última posición se escoje la letra restante En este caso tenemos 3x2x1 = 6 posibilidades

93. Permutación P(n,r)

94. Combinatoria C(n,r) De los objetos de un conjunto, es una selección de estos sin importar el orden. Se divide por r ! ya que en cada combinación existen r ! permutaciones

95. Ejemplo Supongamos que el grupo de probabilidad y estadística está formado por 35 estudiantes. Cuantos grupos de tres estudiantes podrían formarse para hacer un trabajo? La solución es

96. Combinatoria vs Permutación La diferencia entre una permutación y una combinatoria es que en la primera el interés se centra en contar todas las posibles selecciones y todos los arreglos de estas, mientras que en la segunda el interés sólo recae en contar el número de selecciones diferentes. Ejemplo: abc y acb son diferentes permutaciones pero son iguales combinación de las letras

97. Permutación y combinación en MS EXCEL y MATLAB

98. Ejemplo

99. Ejemplo

100. Ejemplo

101. Ejemplo