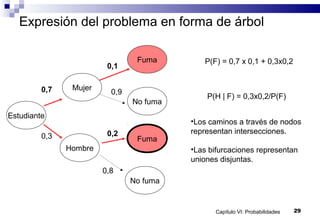
El documento presenta conceptos básicos sobre probabilidad. Explica que la probabilidad es una medida de la posibilidad de que ocurra un suceso futuro. Define experimentos, espacio muestral, sucesos y eventos. Describe las propiedades de la probabilidad y cómo se calcula la probabilidad clásica y frecuencial. También cubre probabilidad condicional, independencia de sucesos, teorema de la probabilidad total y teorema de Bayes.

1. Capítulo VI: Probabilidades 1
VI. Probabilidad

2. Capítulo VI: Probabilidades 2
 ¿Cuál es la probabilidad de aprobar Estadística?
 ¿Cuál es la probabilidad de no encontrarme con un
taxi cuando voy a clase?
 Todos los días nos hacemos preguntas donde
utilizamos el concepto de probabilidad.
 Probabilidad es una medida de la
posibilidad de que ocurra un suceso futuro.

3. Capítulo VI: Probabilidades 3
Experimentos. Proceso o fenómeno, cuyos
resultados dependen del azar
 Determinísticos
 Aleatorios
AZAR

4. Capítulo VI: Probabilidades 4
Experimento - Espacio muestral
E1 Se arroja un dado :
Si observamos su cara superior, el conjunto
de resultados posibles es
Ω: { 1, 2, 3, 4, 5, 6 }

5. Capítulo VI: Probabilidades 5
 E2 Se arrojan dos dados y se observa la
suma de sus caras.
Ω 2,3,4,5,6,7,8,9,10,11,12

6. Capítulo VI: Probabilidades 6
E3 :Se arroja una moneda hasta que
aparezca cara.
Ω { C, XC, XXC, XXXC, XXXXC, ..., X..XC, .... }

7. Capítulo VI: Probabilidades 7
Ejemplo : Sea el experimento arrojar dos dados.
El conjunto de resultados posibles es:
= {(x,y)/ x = 1, 2 .. 6, y = 1, 2 ..
6 }
Ω
Ω
A = {(x,y) / x + y = 5 }
A = {(1,4), (2,3), (3,2), (4,1)}
A
X1 2 3 4 5 6
Y
6
5
4
3
2
1

8. Capítulo VI: Probabilidades 8
Sucesos
E espacio muestral
E espacio muestral
A
A’
Cuando se realiza un experimento aleatorio diversos resultados son
posibles. El conjunto de todos los resultados posibles se llama espacio
muestra (Ω).
Se llama suceso a un subconjunto de dichos resultados.
Se llama suceso complementario de un suceso A, A’,
al formado por los elementos que no están en A

9. 9
Realmente lo compró
Planea comprarlo Sí No Total
Sí 200 50 250
No 100 650 750
Total 300 700 1,000
 ¿Qué es un espacio muestral? Dé ejemplos de eventos simples
y eventos conjuntos.
Ejemplo. Encuesta para compra de un televisor
Solución: El espacio muestral consiste en las 1,000 persona
encuestadas. Los eventos simples son “si planea comprarlo”, “no
planea comprarlo”. “si compra”, y “no compra”. El complemento del
evento “planea comprarlo” es “no planea comprarlo”. El evento
“planea comprarlo y realmente lo compra” es un evento conjunto.

10. Capítulo VI: Probabilidades 10
E espacio muestral
A
B
Se llama suceso unión de A con B, AUB, al formado por los
resultados experimentales que están en A o en B (incluyendo los
que están en ambos).
E espacio muestral
A
B
UNIÓN
Se llama suceso intersección de A y B, A∩B o simplemente
AB, al formado por los resultados experimentales que están
simultáneamente en A y B
E espacio muestral
A
B
INTERSEC.

11. Capítulo VI: Probabilidades 11
DEFINICIÓN CLÁSICA DE PROBABILIDAD.
Sea A un subconjunto de Ω, simbolizando con #A al cardinal de
A que indica el número de casos favorables al suceso A,
calculamos la probabilidad de dicho suceso (siempre que sea
equiprobable) como el cociente:
P A
A número de resultados favorables
número de resultados posibles
( )
#
#
= =
Ω

12. Capítulo VI: Probabilidades 12
PROPIEDADES
PROPIEDAD 1 0 ≤P(A) ≤ 1
1)(0
#
#
#
#
#
0
≤≤⇒
Ω
Ω
≤
Ω
≤
Ω
AP
AComo 0 ≤ #A ≤ # Ω
#
# #
( )
∅
= ⇒ ∅ =
Ω Ω
0
0P
PROPIEDAD 2
Como #∅ = 0
P(∅ )= 0
PROPIEDAD 3 P(Ω) =1
1
#
#
=
Ω
Ω
Ya que P(Ω ) =

13. Capítulo VI: Probabilidades 13
PROPIEDAD 4 P (A∪B) = P(A) + P(B), si A∩B =∅
P A B
A B A B A B
P A P B( )
#( )
#
# #
#
#
#
#
#
( ) ( )∪ =
∪
=
+
= + = +
Ω Ω Ω Ω
Si A∩B = ∅, entonces #(A∪B) = #A + #B.
PROPIEDAD 5 P (A∪B) = P(A) + P(B)- P(A∩B) si A∩B ≠∅
∴ ∪ = =
+ − ∩
= + −
∩
∴ ∪ = + − ∩
P A B
AUB A B A B A B A B
P A B P A P B P A B
( )
#( )
#
# # #( )
#
#
#
#
#
#( )
#
( ) ( ) ( ) ( )
Ω Ω Ω Ω Ω
PROPIEDAD 6 P( ) = 1 - P(A)A
P A
A A A
P A( )
#( )
#
# #
#
#
#
#
#
( )= =
−
= − = −
Ω
Ω
Ω
Ω
Ω Ω
1
A
A’
A
B
A
B

14. Capítulo VI: Probabilidades 14
Ejemplo:
En una agencia bancaria hay dos sistemas de alarma A y
B. El sistema A funciona en 7 de cada 10 atracos, B
funciona en 8 de cada 10 y los dos a la vez lo hacen 6 de
cada 10 atracos.
¿Cuál es la probabilidad de que en caso de atraco
funcione al menos una de estas alarmas?
Solución:
Se definen los sucesos
A:”El sistema A funciona”
B:”El sistema B funciona”
9,06,08,07,0)(
6,0)(8,0)(7,0)(
=−+=
=∩==
BUAP
BAPBPAP

15. Capítulo VI: Probabilidades 15
DEFINICIÓN FRECUENCIAL DE PROBABILIDAD.
Si se repite un experimento una gran cantidad de veces y se observa la aparición de
un resultado (suceso A) podrá notarse que la frecuencia relativa del suceso tiende a
estabilizarse en un valor a medida que crece el número de repeticiones del
experimento.
Simbolizando con f a la cantidad de veces que apareció el suceso A como resultado
del experimento, y con n a la cantidad de veces que se repitió el experimento
n
lim
f
n
p
→∞
=
La frecuencia relativa del suceso se estabiliza en un valor que es la probabilidad
teórica del suceso A y la propia frecuencia relativa es la probabilidad empírica del
suceso A.
Asociada a cada suceso existe una probabilidad teórica, a la cual tiende la
frecuencia relativa del mismo a medida que aumenta la cantidad de repeticiones
del experimento.

16. Capítulo VI: Probabilidades 16
n f h n f h
10 6 0,60 110 56 0,51
20 8 0,40 120 63 0,53
30 14 0,47 130 61 0,47
40 19 0,48 140 72 0,51
50 25 0,50 150 75 0,50
60 31 0,52 160 78 0,49
70 38 0,54 170 83 0,49
80 43 0,54 180 89 0,49
90 46 0,51 190 95 0,50
100 51 0,51 200 101 0,50
n
h
0,35
0,4
0,45
0,5
0,55
0,6
0,65
0 50 100 150 200 250

17. Capítulo VI: Probabilidades 17
PROBABILIDAD DE LA UNIÓN DE SUCESOS
P (A∪B) = P(A) + P(B), si A∩B =∅
P (A∪B ∪C) = P(A) + P(B) + P(C), si A∩B∩C =∅
Sucesos Excluyentes
Sucesos No Excluyentes
P (A∪B) = P(A) + P(B)- P(A∩B)

18. Capítulo VI: Probabilidades 18
PROBABILIDAD CONDICIONAL
Se llama probabilidad de A condicionada a B, o probabilidad de A
sabiendo que pasa B:
)(
)(
)|(
BP
ABP
BAP =
E espacio muestral
A
B

19. Capítulo VI: Probabilidades 19
Probabilidad condicionada
B
A
P(A) = 0,25
P(B) = 0,10
P(AB) = 0,10
B
A
¿Probabilidad de A dado B?
P(A|B)=1 P(A|B)=0,8
P(A) = 0,25
P(B) = 0,10
P(AB) = 0,08

20. Capítulo VI: Probabilidades 20
Probabilidad condicionada
A
B
A
B
¿Probabilidad de A dado B?
P(A|B)=0,05 P(A|B)=0
P(A) = 0,25
P(B) = 0,10
P(AB) = 0,005
P(A) = 0,25
P(B) = 0,10
P(AB) = 0

21. Capítulo VI: Probabilidades 21
 Dos sucesos son independientes si la
ocurrencia de uno no añade información sobre
el otro. En lenguaje probabilístico:
 A indep. B  P(A|B) = P(A)
 Dicho de otra forma:
 A indep. B  P(AB) = P(A) P(B)

22. 22
 Ejemplo. En un banco de sangre se
determinaron los grupos sanguíneos:
¿Cuál es la probabilidad de que las siguientes dos
personas sean del grupo 0?
Grupo n %
0 45 45
A 29 29
B 21 21
AB 5 5
Total 100 100

23. Capítulo VI: Probabilidades 23
 El hecho de que la siguiente personas sea
del grupo 0 no impide que la segunda, sea
del grupo 0, por lo tanto es independiente.
 Sus probabilidades individuales, se
multiplican: P(OO) = P(O) P(O)
 0.45 x 0.45 = 0.2025 = 20.25%

24. Capítulo VI: Probabilidades 24
 Ejemplo
100 recién nacidos en un maternidad de
Huánuco
 55 fueron mujeres y 45 hombres
 La probabilidad de ser mujer fue de 55/100 = 0.5
 La probabilidad de ser hombre fue de 45/100=0.4
¿Cuál es la probabilidad de que los siguientes tres
nacimientos sean mujeres?
 Son eventos mutuamente excluyentes, por lo
tanto se multiplican las probabilidades
individuales.
 0.55 x 0.55 x 0.55 = 0.1664 = 16.64%

25. Capítulo VI: Probabilidades 25
Sistema exhaustivo y excluyente de sucesos
A1 A2
A3 A4
Son una colección de sucesos
A1, A2, A3, A4…
Tales que la unión de todos ellos forman
el espacio muestral, y sus intersecciones
son disjuntas.

26. Capítulo VI: Probabilidades 26
A1 A2
A3 A4
B
Todo suceso B, puede ser
descompuesto en componentes
de dicho sistema.
B = (B∩A1) U (B∩A2 ) U ( B∩A3 ) U ( B∩A4 )
Nos permite descomponer el problema B en
subproblemas más simples..

27. Capítulo VI: Probabilidades 27
Teorema de la probabilidad total
A1 A2
A3 A4
B
Si conocemos la probabilidad de B en
cada uno de los componentes de un
sistema exhaustivo y excluyente de
sucesos, entonces…
… podemos calcular la probabilidad de B.
P(B) = P(B∩A1) + P(B∩A2 ) + P( B∩A3 ) + ( B∩A4 )
=P(B|A1) P(A1) + P(B|A2) P(A2) + …

28. Capítulo VI: Probabilidades 28
 P(H|F) = P(F ∩ H)/P(F)
= P(F|H) P(H) / P(F)
= 0x2 x 0,3 / 0,13
= 0,46 = 46%
Mujeres
Varones
fumadores
Ejemplo: En esta aula el 70% de los alumnos son mujeres. De
ellas el 10% son fumadoras. De los varones, son fumadores el
20%.
T. Prob. Total.
Hombres y mujeres forman
Un Sist. Exh. Excl.
De sucesos
T. Bayes
¿Qué porcentaje de fumadores hay en total?
P(F) = P(F∩H) + P(F∩M)
= P(F|H) P(H) + P(F|M) P(M)
=0,2 x 0,3 + 0,1 x 0,7
= 0,13 =13%
¿Se elije a un individuo al azar y resulta
fumador. ¿Cuál es la probabilidad de que sea un hombre?
0.70
0.30
0.10
0.20

29. Capítulo VI: Probabilidades 29
Expresión del problema en forma de árbol
Estudiante
Mujer
No fuma
Hombre
Fuma
No fuma
Fuma
0,7
0,1
0,20,3
0,8
0,9
P(F) = 0,7 x 0,1 + 0,3x0,2
P(H | F) = 0,3x0,2/P(F)
•Los caminos a través de nodos
representan intersecciones.
•Las bifurcaciones representan
uniones disjuntas.

30. Capítulo VI: Probabilidades 30
Teorema de Bayes
A1 A2
A3 A4
B
Si conocemos la probabilidad de B en cada
uno de los componentes de un sistema
exhaustivo y excluyente de sucesos,
entonces…
…si ocurre B, podemos calcular la
probabilidad (a posteriori) de ocurrencia de
cada Ai.
P(B) se puede calcular usando el teorema de la probabilidad total:
P(B)=P(B∩A1) + P(B∩A2 ) + P( B∩A3 ) + ( B∩A4 )
=P(B|A1) P(A1) + P(B|A2) P(A2) + …
P(B)
Ai)P(B
B)|P(Ai =