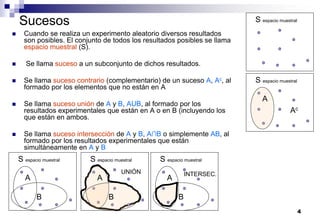
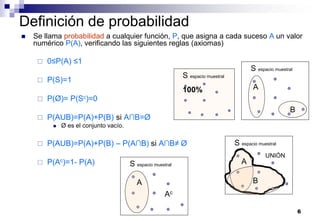
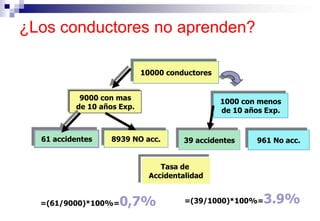
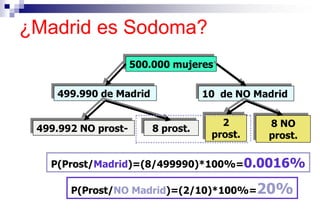
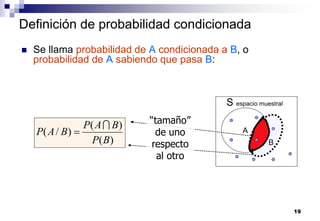
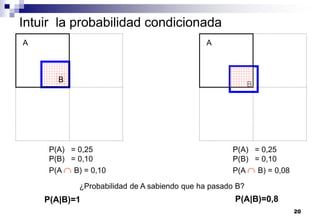
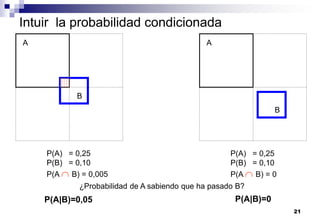
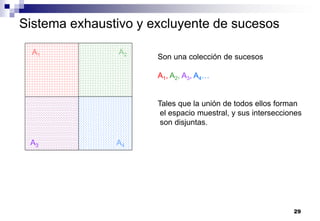
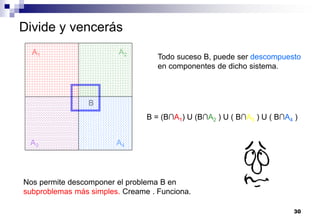
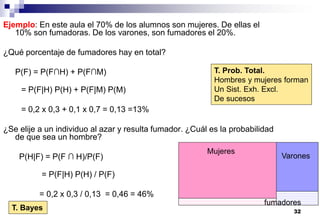
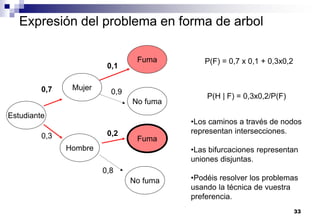
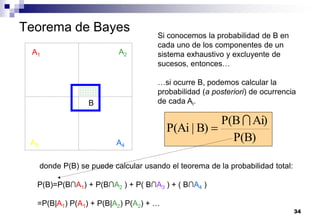
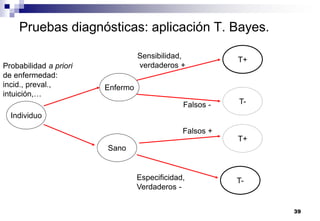
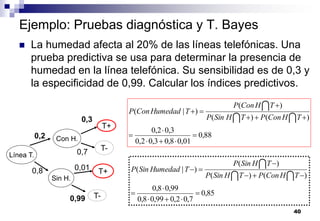
El documento aborda las nociones básicas de probabilidad y su aplicación en diferentes contextos, como la estadística y situaciones cotidianas. Se explican conceptos fundamentales como sucesos, espacio muestral y funciones de probabilidad, junto con ejemplos prácticos para calcular probabilidades. Además, se introducen las reglas de cálculo de probabilidad y conceptos de probabilidad condicionada en el análisis de datos.

1. 1
Probabilidad y
Estadística
Nociones Básicas de Probabilidad

2. 2
 ¿Cuál es la probabilidad de aprobar este curso de Estadística?
 ¿Cuál es la probabilidad de no encontrarme un trancon en la Vía
Cali-Jamundi cuando voy a clase?
 Todos los días nos hacemos preguntas sobre probabilidad e
incluso los que hayan visto poco de la materia en cursos
anteriores, tienen una idea intuitiva lo suficientemente correcta
para lo que necesitamos de ella en este curso.
 En este tema vamos a:
 Recordar teoría básica de conjuntos
 Entender el concepto de probabilidad.
 Aprender algunas reglas de cálculo de probabilidad
 Ver cómo aparecen las probabilidades en problemas aplicados.

3. 3
Nociones de probabilidad
 Hay dos maneras principales de entender la probabilidad:
 Frecuentista (objetiva): Probabilidad de un suceso es la frecuencia
relativa (%) de veces que ocurriría el suceso al realizar un experimento
repetidas veces.
 Subjetiva (bayesiana): Grado de certeza que se posee sobre un
suceso. Es personal.
 En ambos tipos de definiciones aparece el concepto de
suceso. Vamos a recordar qué son y algunas operaciones
que se pueden realizar con sucesos.

4. 4
Sucesos
 Cuando se realiza un experimento aleatorio diversos resultados
son posibles. El conjunto de todos los resultados posibles se llama
espacio muestral (S).
 Se llama suceso a un subconjunto de dichos resultados.
 Se llama suceso contrario (complementario) de un suceso A, Ac, al
formado por los elementos que no están en A
 Se llama suceso unión de A y B, AUB, al formado por los
resultados experimentales que están en A o en B (incluyendo los
que están en ambos.
 Se llama suceso intersección de A y B, A∩B o simplemente AB, al
formado por los resultados experimentales que están
simultáneamente en A y B
S espacio muestral
S espacio muestral
A
Ac
S espacio muestral
A
B
S espacio muestral
A
B
UNIÓN
S espacio muestral
A
B
INTERSEC.

5. 5
En un Plan de estudio de 1000 estudiantes se encontró que:
420 fuman, 516 consumen bebidas alcohólicas, 332 comen entre comidas,
244 fuman y consumen bebidas alcohólicas,
166 comen entre comidas y consumen bebidas alcohólicas,
194 fuman y comen entre comidas y
104 tienen estos tres hábitos nocivos para la salud.
Ejemplo
104
F
C
A
90
62
140
86
210
76
232
S
Determine cuantos estudiantes:
• Fuman pero no consumen
bebidas alcohólicas.
• Comen entre comidas y
consumen bebidas
alcohólicas pero no fuman
• Ni fuman ni comen entre
comidas.
86+90
62
210+232

6. 6
Definición de probabilidad
 Se llama probabilidad a cualquier función, P, que asigna a cada suceso A un valor
numérico P(A), verificando las siguientes reglas (axiomas)
 0≤P(A) ≤1
 P(S)=1
 P(Ø)= P(Sc)=0
 P(AUB)=P(A)+P(B) si A∩B=Ø
 Ø es el conjunto vacío.
 P(AUB)=P(A)+P(B) – P(A∩B) si A∩B≠ Ø
 P(Ac)=1- P(A)
S espacio muestral
100%
S espacio muestral
B
A
S espacio muestral
A
B
UNIÓN
S espacio muestral
A
Ac

7. 7
En un Plan de estudio de 1000 estudiantes se encontró que:
420 fuman, 516 consumen bebidas alcohólicas, 332 comen entre comidas,
244 fuman y consumen bebidas alcohólicas,
166 comen entre comidas y consumen bebidas alcohólicas,
194 fuman y comen entre comidas y
104 tienen estos tres hábitos nocivos para la salud.
Si se seleccionan un miembro al azar de este plan de estudio, encuentre la
probabilidad de que el estudiante:
Ejemplo
• Fuman pero no consumen bebidas
alcohólicas.
• Comen entre comidas y consumen
bebidas alcohólicas pero no fuman
• Ni fuman ni comen entre comidas.
(86+90)/1000=0.176
62/1000=0.062
(210+232)/1000=0.442
104
F
C
A
90
62
140
86
210
76
232
S

8. 8
La probabilidad que una industria colombiana ubique una oficina
en Munich es 0.7 y en Brusela 0.4, que se ubique en ambas
ciudades es 0.3
P(M) = 0.7 P(B) = 0.4 P(MB) = 0.3
S espacio muestral
M
B
UNIÓN
Ejemplo
¿Cuál es la probabilidad que la compañía ubique
una oficina en una de estas dos ciudades?
P(MB) = P(M) + P(B) - P(MB)
= 0.7 + 0.4 - 0.3 = 0.8
¿Cuál es la probabilidad que la compañía no
ubique oficina en ninguna de estas dos
ciudades?
P((MB)C) = 1 - P(MB) = 1 – 0.8 = 0.2

9. 9
Una caja contiene 500 sobres con dinero asi: 75 sobres contienen US$100, 150
contienen US$25 y 275 sobres contienen US$10. Usted paga US$25 y puede
escoger al azar un sobre de la caja.
¿Cuáles son los posibles resultados de extraer un sobre de la caja, en otras
palabras cual es el espacio Muestral?
S = US$100, US$25, US$10
Asigne probabilidades a cada punto del espacio muestral.
P(US$100) = 0.15 P(US$25) = 0.3 P(US$10) = 0.55
¿Cual es la probabilidad que el primer sobre que se saque de la caja
contenga menos de US$100? Note que los US$25 y US$10 eventos son
excluyentes.
P(US$25  US$10) = P(US$25) + P(US$10) = 0.55 + 0.3 = 0.85
Ejemplo

10. 10
Una caja contiene 500 sobres con dinero asi: 75 sobres contienen US$100, 150
contienen US$25 y 275 sobres contienen US$10. Usted paga US$25 y puede
escoger al azar un sobre de la caja.
P(US$100) = 0.15 P(US$25) = 0.3 P(US$10) = 0.55
¿Cuál es la probabilidad de que usted no pierda en este juego? Note que
los US$25 y US$100 eventos son excluyentes.
P(US$25  US$100) = P(US$25) + P(US$100) = 0.3 + 0.15= 0.45
¿Cuál es la probabilidad de que usted pierda en este juego?
P((US$25  US$100)c) = 1 - P(US$25  US$100) = 1 - 0.45 = 0.55
O lo que es lo mismo P(US$10) = 0.55
Ejemplo

11. 11
900 estudiantes de un plan de estudio nocturno se clasificaron de acuerdo
a su sexo y su situación laboral, a continuación se presenta el resultado de
esta clasificación.:
Empleado Desempleado Total
Hombre 460 40 500
Mujer 140 260 400
Total 600 300 900
Situación Laboral
Sexo
Ejemplo
Si se selecciona un estudiante al azar ¿cual es la probabilidad de encontrar:
Un Hombre?
Una Mujer?
Un Empleado?
Un Desempleado?
P(H) = 500/900
P(M) = 400/900
P(E) = 600/900
P(D) = 300/900

12. 12
900 estudiantes de un plan de estudio nocturno se clasificaron de acuerdo
a su sexo y su situación laboral, a continuación se presenta el resultado de
esta clasificación.:
Empleado Desempleado Total
Hombre 460 40 500
Mujer 140 260 400
Total 600 300 900
Situación Laboral
Sexo
Ejemplo
Si se selecciona un estudiante al azar ¿Cual es la probabilidad de encontrar:
Un Hombre y empleado?
Un Hombre y desempleado?
Una Mujer y empleada?
Una Mujer y desempleado?
P(HE) = 460/900
P(HD) = 40/900
P(ME) = 140/900
P(MD) = 260/900

13. 13
P(HM) = P(S) = 1
P(HD) = P(H) + P(D) - P(HD) = 500/900 + 300/900 - 40/900 = 38/45
P(ME) = P(M) + P(E) - P(ME) = 400/900 + 600/900 - 140/900 = 43/45
900 estudiantes de un plan de estudio nocturno se clasificaron de acuerdo
a su sexo y su situación laboral, a continuación se presenta el resultado de
esta clasificación.:
Empleado Desempleado Total
Hombre 460 40 500
Mujer 140 260 400
Total 600 300 900
Situación Laboral
Sexo
Ejemplo
Si se selecciona un estudiante al azar ¿cual es la probabilidad de encontrar:
Un Hombre o una Mujer?
Un Hombre o Desempleado?
Una Mujer o Empleada?

14. 14
 ¿Cuál es la probabilidad de aprobar este curso de
Estadística? Si he aprendido los conceptos, hago los
ejercicios y ya gane mi primer parcial.
 ¿Cuál es la probabilidad de encontrarme un trancón en
la Vía Cali-Jamundi cuando voy a clase? Si cuando
salgo de mi casa esta lloviendo a cantaros.
Noción de probabilidad condicionada

15. ¿Los conductores no aprenden?
 Un estudio de los accidentes de una ciudad
mostró que 61% de los comprometidos en
accidentes tenían más de 10 años de
experiencia; 21% tenían entre 6 y 10 años
solamente; 17% tenían entre 1 y 5 años. Se
concluyó que los choferes entre más años
lleven al volante, se vuelven menos
cuidadosos y como consecuencia sus
probabilidades de accidentarse aumentan.

16. ¿Los conductores no aprenden?
10000 conductores
9000 con mas
de 10 años Exp.
1000 con menos
de 10 años Exp.
61 accidentes 39 accidentes
8939 NO acc. 961 No acc.
Tasa de
Accidentalidad
=(61/9000)*100%=0,7% =(39/1000)*100%=3.9%

17. ¿Madrid es Sodoma?
 Una encuesta entre prostitutas realizadas en
Madrid mostró que un elevado porcentaje de
ellas más del 80% habían nacido Madrid. Se
piensa que quizás la constitución de la
familia y los patrones educativos de esta
zona del país predispongan a esta situación.

18. ¿Madrid es Sodoma?
500.000 mujeres
499.990 de Madrid 10 de NO Madrid
8 prost.
499.992 NO prost-
2
prost.
8 NO
prost.
P(Prost/Madrid)=(8/499990)*100%=0.0016%
P(Prost/NO Madrid)=(2/10)*100%=20%

19. 19
Definición de probabilidad condicionada
 Se llama probabilidad de A condicionada a B, o
probabilidad de A sabiendo que pasa B:
)
(
)
(
)
/
(
B
P
B
A
P
B
A
P


S espacio muestral
A
B
“tamaño”
de uno
respecto
al otro

20. 20
Intuir la probabilidad condicionada
B
A
P(A) = 0,25
P(B) = 0,10
P(A  B) = 0,10
B
A
¿Probabilidad de A sabiendo que ha pasado B?
P(A|B)=1 P(A|B)=0,8
P(A) = 0,25
P(B) = 0,10
P(A  B) = 0,08

21. 21
Intuir la probabilidad condicionada
A
B
A
B
¿Probabilidad de A sabiendo que ha pasado B?
P(A|B)=0,05 P(A|B)=0
P(A) = 0,25
P(B) = 0,10
P(A  B) = 0,005
P(A) = 0,25
P(B) = 0,10
P(A  B) = 0

22. 22
 Cualquier problema de probabilidad puede resolverse en teoría mediante
aplicación de los axiomas. Sin embargo, es más cómodo conocer algunas
reglas de cálculo:
 P(Ac) = 1 - P(A)
 P(AUB) = P(A) + P(B) - P(A  B)
 P(A/B) = P(A  B)/P(B)
 P(A  B) = P(A) P(B|A)=P(B) P(A|B)
 Prob. de que pasen A y B es la prob. de A y que también pase B sabiendo que pasó A.
 Dos sucesos son independientes si la el que ocurra uno no añade
información sobre el otro. En lenguaje probabilístico:
A indep. B  P(A|B) = P(A)
 Dicho de otra forma:
A indep. B  P(A  B) = P(A) P(B)

23. 23
En un Plan de estudio de 1000 estudiantes se encontró que:
420 fuman, 516 consumen bebidas alcohólicas, 332 comen entre comidas,
244 fuman y consumen bebidas alcohólicas,
166 comen entre comidas y consumen bebidas alcohólicas,
194 fuman y comen entre comidas y
104 tienen estos tres hábitos nocivos para la salud.
Si se seleccionan un miembro al azar de este plan de estudio, encuentre la
probabilidad de que el estudiante:
Ejemplo
• Fume, si se sabe que consume bebidas
alcohólicas.
• No Consume bebidas alcohólicas, si se sabe
que fuma.
• Come entre comidas y consume bebidas
alcohólicas , si se sabe que no fuma.
P(F/A) = P(F∩A)/P(A)=244/516
P(Ac/F) = P(F∩Ac)/P(F)=(86+90)/420
104
F
C
A
90
62
140
86
210
76
232
S
P(C∩A/Fc) = P(C∩A ∩ Fc)/ P(Fc)= 62/580

24. 24
La probabilidad que una industria colombiana ubique una oficina
en Munich es 0.7 y en Brusela 0.4, que se ubique en ambas
ciudades es 0.3
P(M) = 0.7 P(B) = 0.4 P(MB) = 0.3
S espacio muestral
M
B
Ejemplo
¿Cuál es la probabilidad que la compañía ubique
una oficina en Munich? Si ya se ubico una oficina
en Bruselas.
P(M/B) = P(MB)/P(B) = 0.3/0.4 = 75%
¿Cuál es la probabilidad que la compañía ubique
una oficina en Bruselas? Si definitivamente no se
va a ubicar oficina en Munich.
P(B/Mc) = P(McB)/P(Mc) = 0.1/0.3 = 33.3%
0.3
0.1
0.4
0.2

25. 25
900 estudiantes de un plan de estudio nocturno se clasificaron de acuerdo
a su sexo y su situación laboral, a continuación se presenta el resultado de
esta clasificación.:
Empleado Desempleado Total
Hombre 460 40 500
Mujer 140 260 400
Total 600 300 900
Situación Laboral
Sexo
Ejemplo
Si se selecciona un estudiante al azar ¿cual es la probabilidad de encontrar:
Un Hombre? Si sabemos que no tiene empleo
Una Mujer? Si sabemos que tiene empleo
Un Empleado? Si sabemos que es Mujer
Un Desempleado? Si sabemos que es Hombre
P(H/D) = 40/300
P(M/E) = 140/600
P(E/M) = 140/400
P(D/H) = 40/500

26. 26
EJEMPLO: En una muestra de 1000 individuos elegidos al azar, entre
una población de enfermos de osteoporosis 760 eran mujeres.
 Si elegimos a un individuo de la población, qué probabilidad hay de que
sea mujer:
 La noc. frec. de prob. nos permite aproximarlo a P(Mujer)=0,76
 ¿Cuál es la probabilidad de que elegido un individuo de la población sea
hombre:
 P(Hombre)=P(Mujerc)=1-0,76=0,24
Se sabe de otros estudios que entre los individuos con osteoporosis,
aprox. la cuarta parte de las mujeres fuman y la tercera parte de los
hombres.
Si elegimos a un individuo al azar de la población de enfermos.
 ¿Qué probabilidad hay de que sea mujer fumadora?
 P(Mujer ∩ Fumar) = P(Mujer) P(Fumar|Mujer)
 P(Mujer) = 0,76 P(Fumar|Mujer) = ¼
 P(Mujer ∩ Fumar) = P(Mujer) P(Fumar|Mujer) = 0,76 x ¼ = 0,19

27. 27
EJEMPLO: En una muestra de 1000 individuos elegidos al
azar, entre una población de enfermos de osteoporosis 760
eran mujeres.
 Se sabe de otros estudios que entre los individuos con
osteoporosis, aprox. la cuarta parte de las mujeres fuman y la
tercera parte de los hombres.
Si elegimos a un individuo al azar de la población de enfermos.
 ¿Qué probabilidad hay de que sea un hombre fumador?
 P(Hombre ∩ Fumar) = P(Hombre) P(Fumar|Hombre)
 P(Hombre) = 0,24 P(Fumar|Hombre) = 1/3
 P(Hombre ∩ Fumar) = P(Hombre) P(Fumar|Hombre) = 0,24 x 1/3 = 0,08

28. 28
EJEMPLO: En una muestra de 1000 individuos elegidos al azar, entre una
población de enfermos de osteoporosis 760 eran mujeres.
Se sabe de otros estudios que entre los individuos con osteoporosis, aprox. la
cuarta parte de las mujeres fuman y la tercera parte de los hombres.
Si elegimos a un individuo al azar de la población de enfermos.
 ¿Qué probabilidad hay de que sea fumador?
 P(Fumar) = P(Hombre ∩ Fumar) + P(Mujer ∩ Fumar)
 P(Mujer ∩ Fumar) = 0.19 P(Hombre ∩ Fumar) = 0.08
 P(Fumar) = P(Hombre ∩ Fumar) + P(Mujer ∩ Fumar) = 0.08 + 0.19 =0.27
 Si se sabe que es fumador, ¿Qué probabilidad hay de que sea Hombre?
 P(Hombre/Fumar) = P(Hombre ∩ Fumar) /P(Fumar)
 P(Hombre ∩ Fumar) = 0.08 P(Fumar) =0.27
 P(Hombre/Fumar) = P(Hombre ∩ Fumar) /P(Fumar) = 0.08/0.27 =0.296

29. 29
Sistema exhaustivo y excluyente de sucesos
A1 A2
A3 A4
Son una colección de sucesos
A1, A2, A3, A4…
Tales que la unión de todos ellos forman
el espacio muestral, y sus intersecciones
son disjuntas.

30. 30
Divide y vencerás
A1 A2
A3 A4
B
Todo suceso B, puede ser descompuesto
en componentes de dicho sistema.
B = (B∩A1) U (B∩A2 ) U ( B∩A3 ) U ( B∩A4 )
Nos permite descomponer el problema B en
subproblemas más simples. Creame . Funciona.

31. 31
Teorema de la probabilidad total
A1 A2
A3 A4
B
Si conocemos la probabilidad de B en cada
uno de los componentes de un sistema
exhaustivo y excluyente de sucesos,
entonces…
… podemos calcular la probabilidad de B.
P(B) = P(B∩A1) + P(B∩A2 ) + P( B∩A3 ) + ( B∩A4 )
=P(B|A1) P(A1) + P(B|A2) P(A2) + …

32. 32
Ejemplo: En este aula el 70% de los alumnos son mujeres. De ellas el
10% son fumadoras. De los varones, son fumadores el 20%.
¿Qué porcentaje de fumadores hay en total?
P(F) = P(F∩H) + P(F∩M)
= P(F|H) P(H) + P(F|M) P(M)
= 0,2 x 0,3 + 0,1 x 0,7 = 0,13 =13%
¿Se elije a un individuo al azar y resulta fumador. ¿Cuál es la probabilidad
de que sea un hombre?
P(H|F) = P(F ∩ H)/P(F)
= P(F|H) P(H) / P(F)
= 0,2 x 0,3 / 0,13 = 0,46 = 46%
Mujeres
Varones
fumadores
T. Prob. Total.
Hombres y mujeres forman
Un Sist. Exh. Excl.
De sucesos
T. Bayes

33. 33
Expresión del problema en forma de arbol
Estudiante
Mujer
No fuma
Hombre
Fuma
No fuma
Fuma
0,7
0,1
0,2
0,3
0,8
0,9
P(F) = 0,7 x 0,1 + 0,3x0,2
P(H | F) = 0,3x0,2/P(F)
•Los caminos a través de nodos
representan intersecciones.
•Las bifurcaciones representan
uniones disjuntas.
•Podéis resolver los problemas
usando la técnica de vuestra
preferencia.

34. 34
Teorema de Bayes
A1 A2
A3 A4
B
Si conocemos la probabilidad de B en
cada uno de los componentes de un
sistema exhaustivo y excluyente de
sucesos, entonces…
…si ocurre B, podemos calcular la
probabilidad (a posteriori) de ocurrencia
de cada Ai.
donde P(B) se puede calcular usando el teorema de la probabilidad total:
P(B)=P(B∩A1) + P(B∩A2 ) + P( B∩A3 ) + ( B∩A4 )
=P(B|A1) P(A1) + P(B|A2) P(A2) + …
P(B)
Ai)
P(B
B)
|
P(Ai



35. 35
Ejemplo: El departamento de personal de una Multinacional ha descubierto que solo el
60% de los candidatos a ingresar a la compañía como Asistentes de Mercadeo están
realmente calificados para el trabajo. De los calificados el 67% tuvo entrenamiento
previo en análisis estadístico de información. De los no calificados el 20% tuvo
entrenamiento previo en análisis estadístico de información. Para ahorrar costos el Jefe
del Departamento de Personal decide solo realizar pruebas de ingreso a los candidatos
que acrediten entrenamiento en análisis estadístico de información, el afirma que el
porcentaje de calificados aumentará. ¿Usted que opina al respecto? Y ¿Cuál seria la
probabilidad de un candidato que no tiene entrenamiento en análisis estadístico de
información clasifique como apto para el cargo?

36. 36
Ejemplo: Para ahorrar costos el Jefe del Departamento de Personal decide solo realizar
pruebas de ingreso a los candidatos que acrediten entrenamiento en análisis estadístico
de información, el afirma que el porcentaje de calificados aumentará. ¿Usted que opina
al respecto? Y ¿Cuál seria la probabilidad de un candidato que no tiene entrenamiento en
análisis estadístico de información clasifique como apto para el cargo?
( ) ( / )* ( ) 0.402
( / ) 0.8340 ( )
( ) ( ) ( ) 0.402 0.08
c
P Q T P T Q P Q
P Q T P Q
P T P Q T P Q T
    
 
( ) ( / )* ( ) 0.198
( / ) 0.3822
( ) ( ) ( ) 0.198 0.32
c c
c
c c c c
P Q T P T Q P Q
P Q T
P T P Q T P Q T
   
 

37. 37
Pruebas diagnósticas
Una prueba diagnóstica sirve para ayudar a mejorar una
estimación de la probabilidad de que un individuo (Equipo,
Cliente) presente una enfermedad (Falla, problema)
 En principio tenemos una idea subjetiva de P(Enfermo)
(P(Falla), P(problema)). Nos ayudamos de…
 Incidencia,
 Porcentaje de nuevos casos de la enfermedad en la población.
 Porcentaje de nuevos casos de fallas en ese tipo de equipo
 Porcentaje de nuevos casos de problemas en ese tipo de cliente
 Prevalencia,
 Porcentaje de la población de persona que presenta una enfermedad.
 Porcentaje de la población de equipos que presenta falla.
 Porcentaje de la población de clientes que presenta el problema.

38. 38
Pruebas diagnósticas
Por otra parte, para confirmar, usamos una prueba diagnóstica. La misma ha sido
evaluada con anterioridad sobre dos grupos de individuos: sanos y enfermos (Sin
fallas y con fallas) (Sin y con problemas)
Así de modo frecuentista se ha estimado:
 Sensibilidad (verdaderos +) = Tasa de acierto sobre enfermos.
= Tasa de aciertos sobre equipos con fallas
= Tasa de aciertos sobre clientes con problemas
 Especificidad (verdaderos -) = Tasa de acierto sobre sanos.
= Tasa de aciertos sobre equipos sin fallas
= Tasa de aciertos sobre clientes sin problemas
 A partir de lo anterior y usando el Teorema de Bayes, podemos calcular las
probabilidades a posteriori (en función de los resultados del test): Índices
predictivos
 P(Enfermo | Test +) = Índice predictivo positivo
 P(Sano | Test -) = Índice predictivo negativo

39. 39
Pruebas diagnósticas: aplicación T. Bayes.
Individuo
Enfermo
T-
Sano
T+
T-
T+
Probabilidad a priori
de enfermedad:
incid., preval.,
intuición,…
Sensibilidad,
verdaderos +
Falsos +
Especificidad,
Verdaderos -
Falsos -

40. 40
Ejemplo: Pruebas diagnóstica y T. Bayes
 La humedad afecta al 20% de las líneas telefónicas. Una
prueba predictiva se usa para determinar la presencia de
humedad en la línea telefónica. Su sensibilidad es de 0,3 y
la especificidad de 0,99. Calcular los índices predictivos.
88
,
0
01
,
0
8
,
0
3
,
0
2
,
0
3
,
0
2
,
0
)
(
)
(
)
(
)
|
(












 

T
H
Con
P
T
H
Sin
P
T
H
Con
P
T
Humedad
Con
P
Línea T.
Con H.
T-
Sin H.
T+
T-
T+
0,3
0,01
0,99
0,7
0,2
0,8
85
,
0
7
,
0
2
,
0
99
,
0
8
,
0
99
,
0
8
,
0
)
(
)
(
)
(
)
|
(












 

T
H
Con
P
T
H
Sin
P
T
H
Sin
P
T
Humedad
Sin
P

41. 41
Observaciones
 En el ejemplo anterior, al analizar una línea
telefónica tenemos una idea a priori sobre
la probabilidad de que tenga Humedad.
 A continuación se realiza una prueba
diagnóstica que nos aportará nueva
información: Presenta humedad o no.
 En función del resultado tenemos una
nueva idea (a posteriori) sobre la
probabilidad de que la línea tenga
humedad.
 Nuestra opinión a priori ha sido
modificada por el resultado de un
experimento.
 Relaciónalo con el método
científico.
- Presenta Humedad. La
probabilidad ahora es del
88%.
-¿Qué probabilidad hay que
la línea tenga humedad?
- En principio un 20%. Le
haremos unas pruebas.