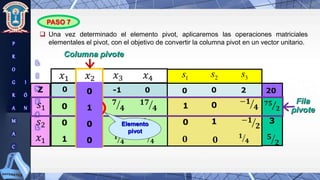
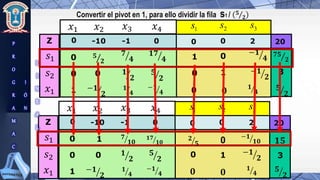
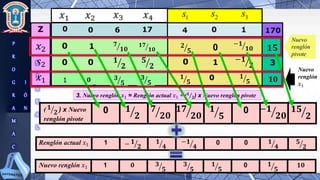
Este documento presenta la resolución de un problema de programación lineal mediante el método simplex. El objetivo es maximizar la función Z = 8x1 + 6x2 + 3x3 - 2x4 sujeto a cuatro restricciones. Se aplican los pasos del método simplex para convertir el problema a forma canónica y resolverlo iterativamente hasta encontrar la solución óptima.