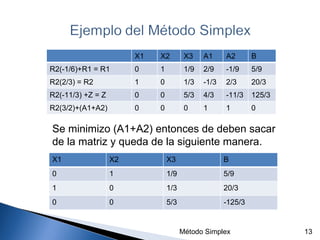
El documento explica los pasos del método de Simplex para resolver problemas de programación lineal, incluyendo la construcción de la matriz inicial, la selección de la columna y fila pivote, y las iteraciones para optimizar la función objetivo sujeto a restricciones. Se provee un ejemplo numérico para maximizar y minimizar funciones objetivo.

1. Presentado por: Natalia Agudelo Vallejo Mabel Johanna Villa Hernández Septiembre / 2011 1 Método Simplex

2. En el algoritmo del Simplex, se parte de un programa base que estará formado por vectores unitarios (vector proceso unitario), realizando iteraciones sucesivas, de manera que en cada uno de ellos, la matriz de coeficientes asociada al programa base sea una matriz identidad. Los pasos a seguir en el algoritmo del Simplex son: 1. Convertir desigualdades en igualdades, introduciendo para ello variables de holgura, que serán positivas en Método Simplex

3. restricciones menores o iguales, y negativas en restricciones mayores o iguales. 2. Obtener el programa base: Esta es la pregunta inicial de la cual partimos para determinar la solución. Para encontrar el programa base, tomaremos un vector unitario de cada una de las restricciones del problema, de acuerdo con el siguiente esquema Método Simplex

4. 2.1. Escoger aquellas variables de holgura con el mismo signo que el término independiente y coeficiente unitario. 2.2. En su defecto, escoger aquellas variables Xi que aparezca en una única restricción, y tenga el mismo signo que el término independiente. Esta variable deberá tener coeficiente unitario. 2.3. En su defecto, introduciremos en aquellas restricciones de las cuales no hemos tocado aún, un vector unitario una variable artificial Kj afectada de un rendimiento –N si estamos maximizando, o de un rendimiento +N si estamos minimizando, y que tendrá un coeficiente unitario. Método Simplex

5. Método Simplex Maximizar Z = X1 + 9 X2 + X3 S.A X1+2X2+3X3 <= 9 3X1+2X2+ 2 X3 <= 15 X1, X2, X3 >=0

6. Se introducen unas variables denominadas de holgura para construir la solución inicial factible. Se construye la matriz inicial Ejemplo del Método Simplex Método Simplex X1 +2X2+ 3X3 + U1= 9 3X1 + 2X2 + 2X3 + U2 = 15 X1 X2 X3 U1 U2 B R1 1 2 3 1 0 9 R2 3 2 2 0 1 15 Z 1 9 1 0 0 0

7. Como se va a maximizar la Z que es la función objetivo, se escoge el valor mayor positivo para hallar la columna de trabajo en este caso seria => 9 la cual se encuentra en X2 Se busca la fila pivote en X2, en las restricciones. Método Simplex R1 2X2 = 9 => X2 = 9/2 X2 = 4.5 R2 2X2= 15 => X2 = 15/2 X2 = 7.5

8. Se construye la nueva matriz con la fila pivote R1 con X2=1 Observemos en Z que todos los coeficientes son negativos o cero (criterios de finalización del algoritmo . ) Método Simplex X1 X2 X3 U1 U2 B R1 1/2 => R1(pivote) ½ 1 3/2 ½ 0 9/2 R1 (-2) + R2 => R2 2 0 -1 -1 1 6 R1 (-9) + Z => Z -7/2 0 -25/2 -9/2 0 -81/2

9. Método Simplex Minimizar Z = 6X1 + 3X2 + 4X3 S.A X1+6X2+X3=10 2X1+3X2+X3=15 X1,X2,X3 >=0

10. Ahora se procede a construir la matriz Se colocan las restricciones en forman estándar Método Simplex X1+6X2+X3+A1=10 2X1+3X2+X3+A2=15 A1= -X1-6X2-X3+10 se despeja A2=-2X1-3X2-X3+15 A1+A2=-3X1-9X2-2X3+25

11. Método Simplex Para definir cual es la columna de trabajo se toma el menor valor negativo que en este caso es -9 ósea que la columna de trabajo es X2. Luego se procese a buscar la fila pivote. X1 X2 X3 A1 A2 B 1 6 1 1 0 10 2 3 1 0 1 15 6 3 4 0 0 0 -3 -9 -2 0 0 -25 R1 6X2=10 => X2= 10/6 X2= 5/3 R2 3X2=15 => X2 = 15/3 X2= 5

12. Método Simplex X1 X2 X3 A1 A2 B R1/6 = R1 1/6 1 1/6 1/6 0 5/3 R1(-39)+R2=R2 3/2 0 ½ -1/2 1 10 R1(-3)+Z= Z 11/2 0 7/2 -1/2 0 -5 R1(9)+(A1+A2)=(A1+A2) -3/2 0 -1/2 3/2 0 -10 R1 1/6X1=5/3 => X1=30/3 X1= 10 R2 3/2 X1=10 => X1 = 10/3/2 X1= 20/3 = 6.6

13. Método Simplex Se minimizo (A1+A2) entonces de deben sacar de la matriz y queda de la siguiente manera. X1 X2 X3 A1 A2 B R2(-1/6)+R1 = R1 0 1 1/9 2/9 -1/9 5/9 R2(2/3) = R2 1 0 1/3 -1/3 2/3 20/3 R2(-11/3) +Z = Z 0 0 5/3 4/3 -11/3 125/3 R2(3/2)+(A1+A2) 0 0 0 1 1 0 X1 X2 X3 B 0 1 1/9 5/9 1 0 1/3 20/3 0 0 5/3 -125/3

14. Método Simplex No se puede minimizar Z ya que las variables de decisión son >= 0. X1= 20/3 X2=5/9 Z=125/3 X3= A1+A2=0