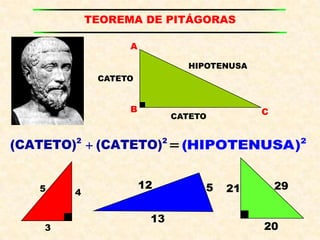
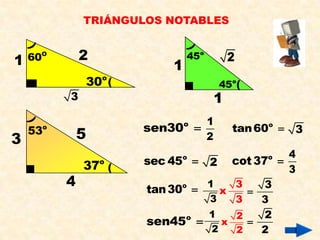
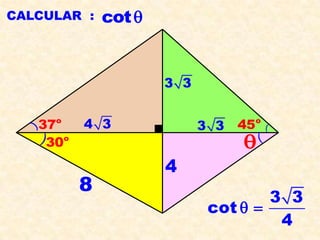
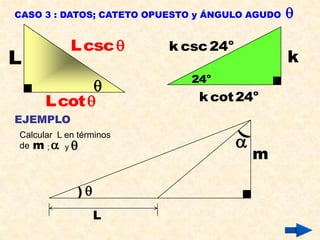
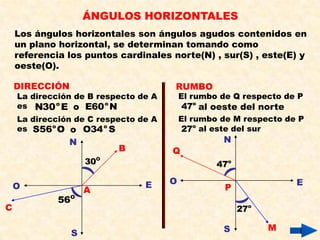
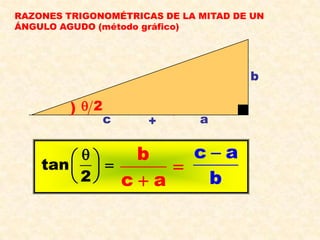
El documento presenta definiciones y propiedades relacionadas con el teorema de Pitágoras, las razones trigonométricas de ángulos agudos, la resolución de triángulos rectángulos y notables, el cálculo de áreas de triángulos, ángulos verticales y horizontales, y la rosa náutica. Se incluyen ejemplos ilustrativos de cada concepto.

3. TEOREMA DE PITÁGORAS
A
HIPOTENUSA
CATETO
B C
CATETO
(CATETO)2  (CATETO)2  (HIPOTENUSA)2
5 12 5 21 29
4
13
3 20

4. RAZONES TRIGONOMÉTRICAS DE ANGULOS
AGUDOS CATETO
HIPOTENUSA
OPUESTO


A
CATETO ADYACENTE A 
SENO COSENO
CatetoOpuestoaq CatetoAdyacentea
senq = cos  
Hipotenusa Hipotenusa
TANGENTE COTANGENTE
CatetoOpuestoa CatetoAdyacentea
tan   cot  
CatetoAdyacentea CatetoOpuestoa
SECANTE COSECANTE
Hipotenusa Hipotenusa
sec   csc  
CatetoAdyacentea CatetoOpuestoa

5. EJEMPLO : TEOREMA DE PITÁGORAS
H
12
H2  122  352
 H  1369  37
35
12 12 37
sen  37
tan 
35
sec   35
35 35 37
cos   cot   csc  
37 12 12
EJEMPLO :
Sabiendo que  es un ángulo agudo tal que sen=2/3.....
3 2


6. PROPIEDADES DE LAS RAZONES
TRIGOMOMÉTRICAS DE ÁNGULOS AGUDOS
RAZONES TRIGONOMÉTRICAS RECÍPROCAS
1 1 1
sen  cos   tan  
csc  sec  cot 
sen csc   1 cos  sec   1 tan  cot   1
EJEMPLOS
1 1
A)  csc 36o B)  sec17o
sen36 o cos17o
C) tan 49o cot 49o  1 D)sen2 csc 2  1
E) cos 63o sec  1   63o
F) tan 2 cot   1 2  

7. PROPIEDADES DE LAS RAZONES
TRIGOMOMÉTRICAS DE ÁNGULOS AGUDOS
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS
PROPIEDAD :
“LAS RAZONES TRIGONOMÉTRICAS DE TODO ÁNGULO AGUDO
SON RESPECTIVAMENTE IGUALES A LAS CO-RAZONES
TRIGONOMÉTRICAS DE SU ÁNGULO COMPLEMENTARIO”
A LAS RAZONES TRIGONOMÉTRICAS SENO Y COSENO
TANGENTE Y COTANGENTE ;SECANTE Y COSECANTE
SE LES DENOMINA :CO-RAZONES TRIGONOMÉTRICAS
sen  cos  cot   tan 

b c cos   sen sec   csc 
 tan  cot  csc   sec 
a

8. EJEMPLOS
A)sen25 o  cos 65o ............... 25o  65o  90O
B) tan 43o  cot 47o ............... 43o  47o  90O
C) sec 60o  csc 30o ............... 60o  30o  90O
D)sen  cos 20o
  20o  90O   70 o
E) tan 5  cot 
5    90 o   15 o
 
F)sen  
5
cos
    3
     rad
5 2 2 5 10

9. TRIÁNGULOS NOTABLES
1 60
O
2 45o 2
1
30o ( 45o(
3 1
1
53 o sen30  o
tan 60o  3
3 5 2
4
37o ( sec 45  2 cot 37 
o o
3
4 tan 30o  1 x 3  3
3 3 3
1 2 2
sen45 o
x 
2 2 2

10. CALCULAR : cot 
3 3
37o 4 3 3 3 45o
30o 
4
8
3 3
cot  
4

11. RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
CASO 1 : DATOS , HIPOTENUSA y ÁNGULO AGUDO 
H
Hsen 5 5sen62o

62o
Hcos 
5 cos 62o
CASO 2 : DATOS ; CATETO ADYACENTE Y ÁNGULO AGUDO 
L sec  8 sec 
L tan 8 tan
 
L 8

12. CASO 3 : DATOS; CATETO OPUESTO y ÁNGULO AGUDO 
L csc  k csc 24o
L k
24o

Lcot  k cot 24o
EJEMPLO

Calcular L en términos
de m ;  y 
m
)
L

13. SOLUCIÓN

m

L mtan
L  m tan 
 cot  L  mtan   mcot 
m
L  mcot   mtan  L  m (cot   tan )
NOTA : DESCOMPOSICIÓN DE UN VECTOR
Y
F Fx  F cos 
Fy
 Fy  Fsen
Fx X

14. ÁREA DEL TRIÁNGULO
C
ab
S senC
2
a
b
bc
S senA
2
A c B ac
S senB
2
EJEMPLO
(5)(8)
S sen60o
2
5m
(5)(8) 3
S ( )  10 3m2
60O 2 2
8m

15. ÁNGULOS VERTICALES
Los ángulos verticales son ángulos agudos contenidos en
un plano vertical y formados por dos líneas imaginarias
llamadas horizontal y visual
ÁNGULO DE ELEVACIÓN
) HORIZONTAL
)
ÁNGULO DE DEPRESIÓN

16. EJEMPLO :
Una persona observa en un mismo plano vertical dos ovnis
volando a una misma altura con ángulos de elevación de
530 y 370 si la distancia entre los ovnis es de 70m ¿A qué
altura están los ovnis?
SOLUCIÓN
70
12k 12k =H
53O 37o
9k +
16k
9k +70 = 16k k = 10 H = 120

17. ÁNGULOS HORIZONTALES
Los ángulos horizontales son ángulos agudos contenidos en
un plano horizontal, se determinan tomando como
referencia los puntos cardinales norte(N) , sur(S) , este(E) y
oeste(O).
DIRECCIÓN RUMBO
La dirección de B respecto de A El rumbo de Q respecto de P
es N30 o E o E60 o N 47o al oeste del norte
La dirección de C respecto de A El rumbo de M respecto de P
es S56o O o O34 o S 27o al este del sur
N N
B Q
30O 47o
E O E
O A P
56 O
C 27o
S M
S

18. ROSA NÁUTICA
Gráfico que contiene 32 direcciones notables, cada dirección
forma entre ellas un ángulo cuya medida es 11 15
o '
En el gráfico adjunto sólo se muestran 16 direcciones notables,
cada una forma entre ellas un ángulo cuya medida es 22o 30'
NNO N NNE
NO NE
ONO ENE
O E
OSO ESE
SO SE
SSO S SSE

19. Las otras 16 direcciones se obtienen trazando las bisectrices de
los 16 ángulos que se muestran en el gráfico anterior.
N 1 4 NO N 1 4 NE
NO 1 4 N NE 1 4 N
N
NNO NNE
NO 1 4 O
NO NE NE 1 4 E
ONO ENE
O 1 4 NO E 1 4 NE
O E
¿Cuánto mide el ángulo entre las direcciones
NE1/ 4N y NO1/ 4O ?
Rpta. 90o

20. EJEMPLO :
Un insecto parte de un punto F y recorre 40 km en la dirección
N530O luego recorre 402 km en la dirección SO, finalmente
recorre 60 km hacia el este. ¿A qué distancia se encuentra el
insecto de F ?
SOLUCIÓN N
OBSERVA QUE EL 45o
TRIÁNGULO DE COLOR
ROJO ES NOTABLE
40
40 2 24
X = 20
53o
O
37o F E
32 x
16 16
45o
40 20 12
60
S

21. RAZONES TRIGONOMÉTRICAS DE LA MITAD DE UN
ÁNGULO AGUDO (método gráfico)

2
c b
)2

2 
c + a
 b ca
tan   
2 c  a b

22. EJEMPLO :
Sabiendo que : tan 8=24/7, calcula tan2
SOLUCIÓN
24
tan 4 
25  7
25 24 tan 4  24
32
4 8 3
25 7 tan 4 
4
3 1
3 5 tan 2  tan 2 
9 3
4 2
4 5