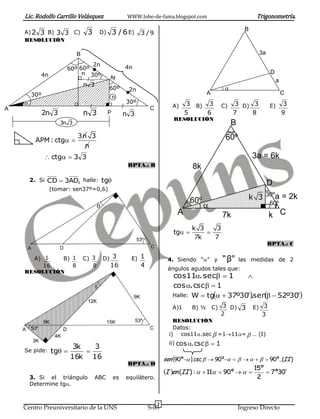
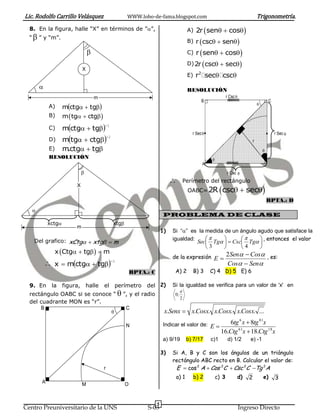
Este documento explica las razones trigonométricas en un triángulo rectángulo. Define las razones trigonométricas como la división de dos lados del triángulo. Establece las relaciones entre las razones trigonométricas de ángulos complementarios. También presenta el teorema del complemento y métodos para resolver triángulos rectángulos calculando lados desconocidos usando las razones trigonométricas de ángulos conocidos.

1. UNIVERSIDAD NACIONAL DEL SANTA
SenA  CO  a CscA  H  b
CEPUNS CosA 
H b
CA c

CO a
SecA  H  b
Ciclo 2013-II H b CA c
CA c
TanA  CO  a CotA  
TRIGONOMETRÍA CA c CO a
“RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO” Semana Nº 3
Razón Trigonométrica: Son aquellos números que Razones Trigonométricas Recíprocas
resultan de dividir dos lados de un triángulo Siendo  un ángulo agudo se cumple:
rectángulo. 1
csc    sen . csc   1 ;
sen
1
sec    cos  . sec   1 ;
cos 
1
ctg   tg .ctg  1
tg
Teorema de Pitágoras: “La suma de los cuadrados
de los catetos es igual al cuadrado de la
Razones Trigonométricas De Ángulos
hipotenusa”
Complementarios
. a2 + b2 = c2
Dos ángulos agudos se llaman complementarios si su
suma es un ángulo recto.
Teorema: “Los ángulos agudos de un triángulo
rectángulo son complementarios”
. A + B = 90º
Definición De Las Razones Trigonométricas Para
Un Ángulo Agudo: Dado el triángulo ABC, recto en
“C”, se establecen las siguientes definiciones:
En la figura se muestra:
 y : Son ángulos complementarios ( +  = 90º)
Cateto Opuesto a Hemos nombrado el ángulo opuesto al cateto b
Sen = =
Hi potenusa c como  y al ángulo opuesto al cateto a como  en
Cateto Adyacente consecuencia:
Cos = = b
Hipotenusa c b a
sen   cos  ; cos    sen
c c
Cateto Opuesto a
tg = = b a
Cateto Adyacente b tg    ctg  ; ctg    tg 
a b
Cateto Adyacente b c c
Ctg = = sec    csc ; csc   sec 
Cateto Opuesto a a b
Hi potenusa c Debido a estas relaciones las co-razones son::
Sec = =  seno y coseno.
Cateto Adyacente b  tangente y cotangente.
Hi potenusa c  secante y cosecante.
csc = =
Cateto Opuesto a Teorema del complemento
RTα  co  RTcomplemento de  
1
Centro Preuniversitario de la UNS S-03 Ingreso Directo

2. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
Se llaman co–razones trigonométricas una de la
67º 30' 75º 71º 30'
otra. 4+ 2 2 10
1 4
6- 2 1
NOTA: 22º 30' 15º 18º 30'
Sen   Csc  1 2+1 6+ 2 3
 Si: 
Cos   Sec   1    
   Ctg  1 RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
Tg
* CÁLCULO DE LADOS: Es el procedimiento
 Si: RT   co  RT       90º mediante el cual se determinan los lados
faltantes de un triángulo rectángulo, en
términos de un lado que sí se conoce; y de un
TRIÁNGULOS RECTÁNGULOS NOTABLES
ángulo agudo que también se conoce.
60º Criterio:
45º
2 2 Lado desconocid o  R.T.( conocido)
1 1 Lado conocido
45º 30º
1 Casos:
3
1.
53º C
5
3 I) BC  Tan   BC 
L
37º AC   AC 
II)
4
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS NOTABLES
 L
A L B
30º 37º 45º 53º 60º
2.
1 3 2 4 3 C
Sen
2 5 2 5 2
I) AB  Cot   AB 
3 4 2 3 1 L
Cos L
2 5 2 5 2 AC   AC 
II)
3 3 4
 L
Tan 1 3 A B
3 4 3
Cot 3
4
1
3 3 3
3 4 3 C
I) BC  Sen   BC 
2 3 5 5
Sec 2 2 L
3 4 3 L
5 5 2 3 AB   
II)
Csc 2
3
2
4 3  L
A B
A partir de estos se determinarán otros
adicionales como: PROBLEMAS RESUELTOS
B
63º 30' 82º 74º
5 5 2 25 1. Halle “ctg” del gráfico, si:
1 120º
1 7
AB  BC
M
26º 30' 8º 16º
2 7 24

A C
2
Centro Preuniversitario de la UNS S-03 Ingreso Directo

3. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
B
A) 2 3 B) 3 3 C) 3 D) 3 / 6 E) 3 / 9
RESOLUCIÓN
B 3a
2n 4n
60º 60º
4n n 30º D
M
a
n 3
60º 2n 
30º A C
n
  30º
A) 3 B) 3 C) 3 D) 3 E) 3
A C
2n 3 n 3 P n 3 5 6 7 8 9
RESOLUCIÓN
3n 3 B
3n 3 60º
APM : ctg 
n
 ctg  3 3 3a = 6k
RPTA.: B 8k
2. Si CD  3AD, halle: tg D
(tomar: sen37º=0,6)
60º k 3 30ºa = 2k
  60º
A 7k k C
k 3 3
tg  
53º 7k 7
RPTA.: C
A D C
A) 1 B) 1 C) 3 D) 3 E) 1 4. Siendo “” y " β" las medidas de 2
16 8 8 16 4
ángulos agudos tales que:
RESOLUCIÓN
cos11. sec  1 
 cos . csc   1
9K Halle: W  tg  37º30' sen   52º30'
. 
12K
A)1 C) 3 D) 3 E) 3
B) ½
2 3
5K 15K 53º RESOLUCIÓN
A 53º D C Datos:
4K i) cos11.sec  =111=  … (I)
3K ii) cos . csc   1
3k 3
Se pide: tg  
16k 16 sen 90º . csc   90º        90º..(II )
RPTA.: D
I en (II ) :   11  90º    15º  7 º30'
3. Si el triángulo ABC es equilátero. 2
Determine tg.
3
Centro Preuniversitario de la UNS S-03 Ingreso Directo

4. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
 15º  165º RESOLUCIÓN
" " enI :   11   82º30'
 2  2
Piden:
W  tg   37 º30'.sen   52º30'  ?
 W  tg 45º .sen 30º   1
2 
RPTA.: B a 2
2a
5. En un triángulo rectángulo si la 45º
hipotenusa es el doble de la media a 2 a 2
geométrica de los catetos. Calcule la suma
a
de las tangentes trigonométricas de los
a
ángulos agudos del triángulo.
A)2 B) 3 C) 4 D)5 E) 6 De la figura: Cot   3
RESOLUCIÓN RPTA.: D
 7. Del gráfico, halle “x”, en términos de “”.
c
a 
 3
b
Si: c  2 ab
Si pide: E  tg  tg 2
2 2
a b a b
E   x
b a ab A) 3cos   2Sen
Pero:
a² + b² = c² B) 2cos   3Sen
 E=
4ab C) 2sen  3cos
 4
ab D) 3sen  2cos
RPTA.: C
E) 2sen  3cos
RESOLUCIÓN
6. En la figura ABCD es un cuadrado, M y N 3Sen
son puntos medios. Determine "cot " .

A B
3

M

2

x
D N C 2Cos
A) 2 B) 1 C) 3 D) ½ E) 1/3
 x  3Sen  2Cos
RPTA.: D
4
Centro Preuniversitario de la UNS S-03 Ingreso Directo

5. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
8. En la figura, halle “X” en términos de ””, A) 2r  sen  cos
“  ” y “m”.
B) r  csc  sen 
 C) r  sen  cos 
X

D) 2r csc  sec 
2
E) r sec csc
 RESOLUCIÓN
m r Csc 
B C
mctg  tg

A)
B) m  tg  ctg 
mctg  tg
1
C)
r Sec  r Sec 
mtg  ctg
1
D) r
E) m.ctg  tg 
RESOLUCIÓN 
A
 r Csc 
 Perímetro del rectángulo
csc  sec
X
OABC= 2R
RPTA.: D

PROBLEMA DE CLASE
xctg xtg
m
1) Si “” es la medida de un ángulo agudo que satisface la
Del grafico: xCtg  xtg  m igualdad:     , entonces el valor
Sec Tg   Csc Tg 
3  4 
x Ctg  tg   m
de la expresión E  2Sen  Cos , es:
 x  mctg  tg 1
Cos  Sen
RPTA.: C A) 2 B) 3 C) 4 D) 5 E) 6
9. En la figura, halle el perímetro del 2) Si la igualdad se verifica para un valor de 'x' en
rectángulo OABC si se conoce “  ”, y el radio

0;
2
del cuadrante MON es “r”.
B C
 x.Senx  x.Cosx. x.Cosx. x.Cosx. ...
N Indicar el valor de: E  6tg 6 x  8tg 81x
16.Ctg 61x  18.Ctg 18 x
a) 9/19 b) 7/17 c)1 d) 1/2 e) -1
3) Si A, B y C son los ángulos de un triángulo
rectángulo ABC recto en B. Calcular el valor de:
r E  cos 2 A  Cos 2C  Csc 2C Tg 2A
a) 1 b) 2 c) 3 d) 2 e) 3
A M O
5
Centro Preuniversitario de la UNS S-03 Ingreso Directo

6. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
4) En la figura AOB es un cuadrante, tal que 2
OD = 4 DE, entonces el valor de tg es: a) 1/3 b) ½ c) 2 d) 2 e) 2 2
3º EXAMEN SUMATIVO 2009 III
8) Se sabe que:
    
Sen a. .Sec  b.   3.tg
 3 2 3 6
y que a  Csc .Csc y b  Sec  .Sec 
Entonces el valor de H       , es:
2.Sec 
 2 
A) 41  1 B) 41  3 C) 41  5 D) 1 E) 1 A) 4 B) 2 C) 6 D) 8 E) 10
4 4 4 4 2
9) Sí 2  3  m ; entonces el valor de
5) Si Sen   40 y 0     , hallar 
Ctg  
 
R = tg7º30` - Ctg 7º 30`, en términos de m es:
41 2 4 a) m/3 b) m/2 c) m d) 2m e) 3m
a) 41  5 b) 41  5 c) 41  3
4 4 4 10) En un triángulo ABC, AC = 10m, <A = 2<B y la
d) 41  3 e) 3 longitud desde el pie de la altura trazada
4 4 desde el vértice C hasta el punto B es igual a
3º EXAMEN SUMATIVO 2010 III 15m, luego el ángulo C mide:
a) 3 b) 3 c)  d) 2 e) 3
6) En la figura mostrada AOD es un cuadrante, M 8 4 2 5 7
y P son puntos de tangencia. Determinar
E=(1 – tg)2. 11) Dada las relaciones:
A Sen(a+b)º=cos(a-b)º
Tg (2a-b).ctg(a+2b) = 1
Calcular el valor de : Tg2 (a+b) + Csc (a-b)
P
a) 1 b) 2 c) 3 d) 4 e) 5
12) En un triángulo AB, se tiene:
 2m<BCA = m<BAC
  Cos(2C) = 1/8 ; c = 4u
0 M B La medida de los lados a y b, respectivamente,
A) 1 B) 2 C) 3 D) 4 E) 5 son:
a) 6u y 7u b) 6u y 4u c) 6u y 5u
d) 6u y 6u e) 6u y 3u
7) En el gráfico mostrado, calcular "tg ".
Si: O y O' son centro y P, Q y T son puntos de 13) Siendo "" angulo agudo, además
tangencia. Csc (40º -2) = Sec(50º+2).tg(20º+)
Calcular el valor de:
5sen (    10 º ) 
k 
cos(    50 º ). sec(  20 º )
a) 5 2 b) 5 2 c) 3 2 d) 5 3 e) 5 2
3 2 2 3
14) De la figura mostrada, determine la longitud
del segmento BD en términos de m, y 
siendo AC=m.
6
Centro Preuniversitario de la UNS S-03 Ingreso Directo

7. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
B
D  

A C
A) m sen.ctgB) m cos.tg
C) m sen.tg  D) m[tg – ctg
E) m cos.ctg
a)5 b) 1/5 c) 1 d) 7/2 e)7/3
15) Siendo ABCD un cuadrado, además 5) Del gráfico halle:
  <26º30', 45º>. Hallar la variación de tgx. W  sen  cos 
A x B
127º
9 10


C) 23 D)  7 E)  23
D C
A)1 B) 7
A) <1/2; 3/4> B) <3/4; 1> 17 17 17 17
C) <1; 2> 6) Si csc2x cos4x=1, calcular el valor de:
V=sen(x+15º)+ctg3x+csc(4x – 30º).
D) <2; 3> E) <3; > A) 2,0 B) 2,5 C)3,0 D) 3,5 E)4,5
7) En la figura mostrada ABCD es un cuadrado,
PROBLEMA DE REPASO calcular csc, DO=OE.
A B
1) Si: sen2x - cos15x = 0 
Calcular el valor de:
E = sen13x.sec4x + tg10x - ctg7x
E
a) -2 b)-1 c)0 d) 1 e) 2
O
37 °
2) Calcular aproximadamente el valor de: D C
 37 º   53º 
2ctg 
 4   3ctg  4 
  
4 41 41
    A) 41 B) 41 C) 4
a) 10 b) 10  5 c) 5 d) 3 10  2 5 41 4 41
e) 2 10  3 5 D) 5 E) 5
3) Si: E  x 2  y 2sen 20 ºxy (cos 70 º1) . 8) Se tiene la región triangular ABC, si AC=a,
2
x  y cos 70 ºxy (sen 20 º1)
2 m ACB  m BAR   .
Reducir: 1  E M
AB
1E Halle: sen cos 
a) x b) y c) y d) e) 3y
B
2x
R
y x 2x y x

4) Del gráfico. Halle: W  sec2   tg2 C
A
7
Centro Preuniversitario de la UNS S-03 Ingreso Directo

8. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
A) a sec2 B)a sen2 C)a cos2 A) 2tgC B) TgB + TgC C) 2tgB
2 2 D) tgC + ctgC E) 2(tgC + tgB)
D) a tg E) a ctg
14) Del gráfico que se muestra encontrar el valor
9) En la figura mostrada M es punto medio de
de 6x+4y, si se sabe que BC=12m y BM es
AC , m BCD  60º , AM=MD=2u. Hallar 4BN.
mediana relativa a la hipotenusa.
D
B
A
M °
37
B N C y
x
 6  2
6
2
A) 2 B) 6 2 C)
4 6  2 A M C
D) 2 2  6 E) A) 20 B)21 C) 24 D)25 E) 28
10) En la figura mostrada ABCD es un rectángulo, 15) Con los datos de la figura si tg 76º =4,
AM=PC=a, MB=3a, BP=2a y m MPD  xº . entonces el valor de “x” es:
Halle E=tgx – 1.
A M B
P
D C
A) 0,1 B) 0,2 C) 0,3 D) 0,4 E) 0,5
A) 6 B) 8 C) 12 D) 18 E) 24
11) En la figura mostrada, ABCD es un cuadrado y
M es un punto medio del lado AB. Hallar ctg . 
sen   cos    0
D C
16) Si:
2
 
tg    cot  0
 3   2 

Calcular:
   
sen    cos   tg36º .tg  
 22   2 
A M B 2 3
A) 5 B)4 C) 3 D) 2 E) 1 a) 0 b ) ½ c) 1 d) 2 e) 3
12) Halle el valor aproximado de: 17) Si los catetos de un triángulo rectángulo son
 53º   37º  como 3 es a 5, el coseno del ángulo agudo
E  Ctg    Ctg    5  10
 4   4  mayor Es:
A) 2 B)3 C) 4 D)5 E) 6 1 3 34
a) 1 b) c) d) 3 e)
43 34 34 43 3
13) En un triángulo BAC, recto en A, la mediana BM
y el cateto AC forman un ángulo x; luego tgx es
igual a:
8
Centro Preuniversitario de la UNS S-03 Ingreso Directo