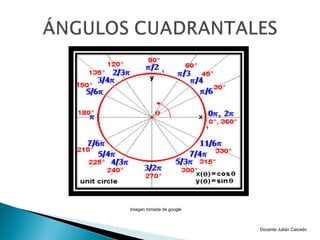
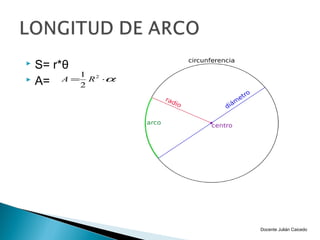
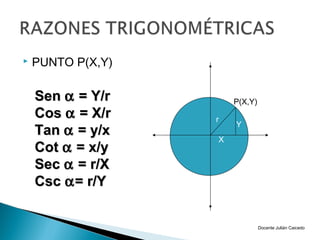
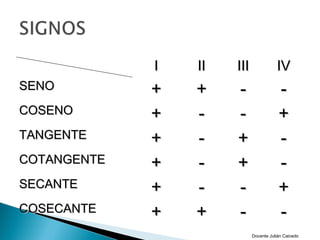
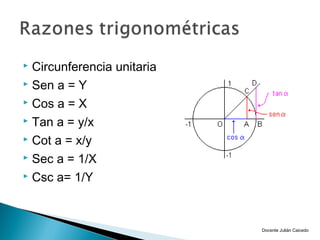
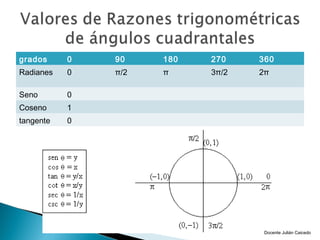
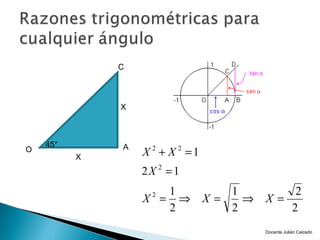
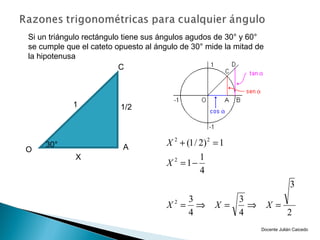
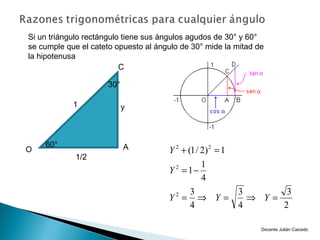
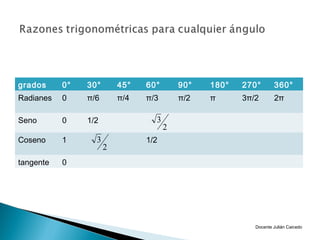
El documento presenta información sobre ángulos. Define qué es un ángulo y cómo se puede medir, ya sea en sentido positivo o negativo. Explica conceptos como ángulos coterminales, centrales y en posición normal. Además, cubre temas como la conversión entre grados, minutos, segundos y radianes, y las funciones trigonométricas como seno, coseno y tangente.

1. Docente Julián Caicedo

2.  Un ángulo se forma por la rotación de una
semi-recta sobre su extremo.
 El ángulo se puede medir en sentido
positivo o sentido negativo.
Docente Julián Caicedo

3.  Ángulo en posición normal :
ángulo ubicado dentro de un sistema
de coordenadas y su vértice coincide
con el origen del sistema
 Ángulos coterminales : ángulos
que coinciden en su lado inicial y lado
final.
 Angulo central : aquél que su
vértice está en el centro de la
circunferencia.
Docente Julián Caicedo

4.  EJEMPLOS:
 Un ángulo de 390°
El ángulo da una vuelta(360°) y sobran
30°; es decir, son coterminales 30° y
360°
 Un ángulo de 1290°
1290 ÷ 360 = 3 vueltas y sobran 210°
Docente Julián Caicedo

5. Imagen tomada de google
Docente Julián Caicedo

6. •SISTEMA SEXAGESIMAL
•Se mide en grados minutos y segundos
1 grado sexagesimal = 60′ (minutos
sexagesimales).
1 minuto sexagesimal = 60″ (segundos
sexagesimales).
1’ = (1/60)°
1” = (1/60)′ = (1/3600)°
Notación Decimal: 23,2345°
Notación sexagesimal: 12°34′34″
Docente Julián Caicedo

7.  Para pasar de grados a minutos multiplica por 60
 Para pasar de minutos a segundos multiplica por 60
 Para pasar de grados a segundos multiplica por 3600
 Para pasar de segundos a minutos divide por 60
 Para pasar de minutos a grados divide por 60
 Para pasar de segundos a grados divide por 3600
 Ejemplo: pasar 40° a segundos: 40 X 3600=144000
 Pasar 1800” a minutos: 1800/60=30’
Docente Julián Caicedo

8.  Pasar de forma decimal en grados a sexagesimal
(grados, min, segundos)
 Ejemplo: pasar 32,47° a sexagesimal:
 32° + 0,47°
 0,47 X 60 = 28,2’ 28’ + 0,2’
 0,2’ X 60 = 12” 32° 28’
12”
 Pasar de grados min y seg a decimal en gados:
 40° 24’ 12” a decimal: 40° + 24/60 + 12/3600=
40,40°
Docente Julián Caicedo

9.  El radián se define como el ángulo que limita un arco de
circunferencia cuya longitud (curva) es igual a la del
radio (recta) de la circunferencia. Es la unidad del
ángulo plano en el Sistema Internacional de Unidades
conocido por SI. Su símbolo es rad
Docente Julián Caicedo

10. Docente Julián Caicedo

11.  S= r*θ
1
 A= A = R ⋅α
2
2
Docente Julián Caicedo

12.  PUNTO P(X,Y)
Sen α = Y/r P(X,Y)
Cos α = X/r r
Y
Tan α = y/x
X
Cot α = x/y
Sec α = r/X
Csc α = r/Y
Docente Julián Caicedo

13. I II III IV
SENO + + - -
COSENO + - - +
TANGENTE + - + -
COTANGENTE + - + -
SECANTE + - - +
COSECANTE + + - -
Docente Julián Caicedo

14.  Circunferencia unitaria
 Sen a = Y
 Cos a = X
 Tan a = y/x
 Cot a = x/y
 Sec a = 1/X
 Csc a= 1/Y
Docente Julián Caicedo

15. grados 0 90 180 270 360
Radianes 0 π/2 π 3π/2 2π
Seno 0
Coseno 1
tangente 0
Docente Julián Caicedo

16. C
X
45° A
O
X X 2 + X 2 =1
2X 2 = 1
1 1 2
X = ⇒
2
X= ⇒ X=
2 2 2
Docente Julián Caicedo

17. Si un triángulo rectángulo tiene sus ángulos agudos de 30° y 60°
se cumple que el cateto opuesto al ángulo de 30° mide la mitad de
la hipotenusa
C
1 1/2
30° A X 2 + (1 / 2) 2 = 1
O
X 1
X = 1−
2
4
3
3 3
X2 = ⇒ X= ⇒ X=
4 4 2
Docente Julián Caicedo

18. Si un triángulo rectángulo tiene sus ángulos agudos de 30° y 60°
se cumple que el cateto opuesto al ángulo de 30° mide la mitad de
la hipotenusa
C
30°
1 y
60° A
O Y 2 + (1 / 2) 2 = 1
1/2
1
Y 2 = 1−
4
3 3 3
Y2 = ⇒ Y = ⇒ Y=
4 4 2
Docente Julián Caicedo

19. grados 0° 30° 45° 60° 90° 180° 270° 360°
Radianes 0 π/6 π/4 π/3 π/2 π 3π/2 2π
Seno 0 1/2 3
2
Coseno 1 3 1/2
2
tangente 0
Docente Julián Caicedo