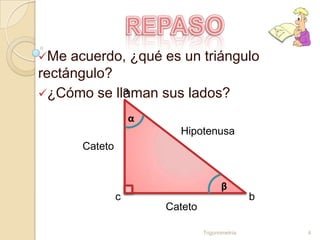
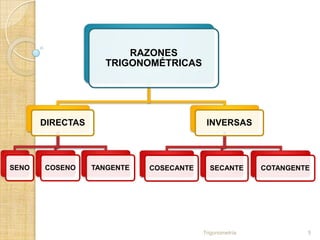
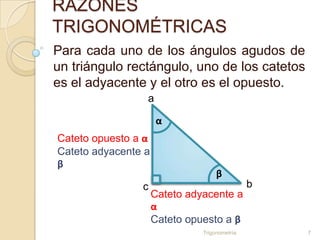
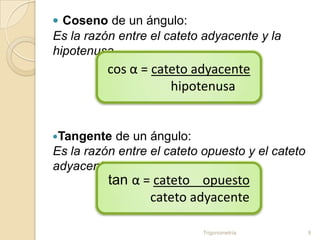
Este documento presenta una lección sobre las razones trigonométricas de un triángulo rectángulo. Explica las definiciones de seno, coseno y tangente para los ángulos agudos, y también las razones inversas. Proporciona ejemplos para ilustrar cómo calcular los lados desconocidos usando las razones trigonométricas. Además, describe los pasos para resolver triángulos rectángulos cuando se conocen ángulos y/o lados.