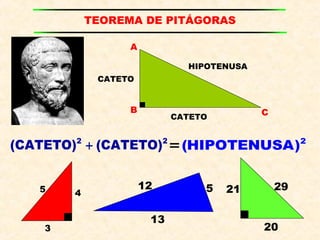
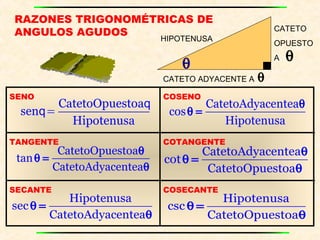
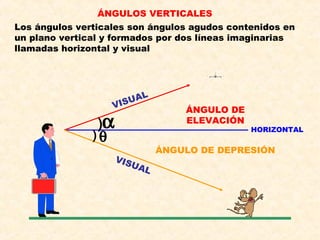
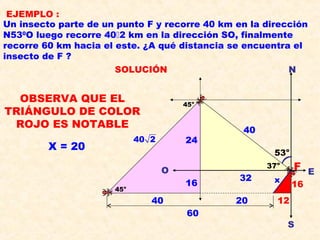
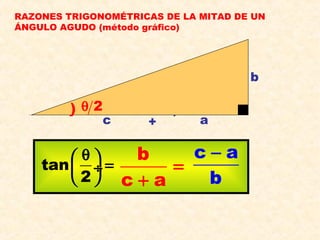
El documento presenta los conceptos fundamentales de las razones trigonométricas de ángulos agudos, incluyendo definiciones de seno, coseno, tangente, cotangente, secante y cosecante. También explica propiedades como las razones trigonométricas recíprocas y de ángulos complementarios, y presenta ejemplos de cálculos de razones trigonométricas para triángulos rectángulos y especiales. Por último, introduce conceptos de ángulos verticales y horizontales.

2. TEOREMA DE PITÁGORAS
A
HIPOTENUSA
CATETO
B C
CATETO
(CATETO) + (CATETO)
2 2
= (HIPOTENUSA) 2
5 12 5 21 29
4
13
3 20

3. RAZONES TRIGONOMÉTRICAS DE
ANGULOS AGUDOS CATETO
HIPOTENUSA
OPUESTO
θ
θ
A
CATETO ADYACENTE A θ
SENO COSENO
CatetoOpuestoaq CatetoAdyacenteaθ
senq = cos θ =
Hipotenusa Hipotenusa
TANGENTE COTANGENTE
CatetoOpuestoaθ CatetoAdyacenteaθ
tan θ = cot θ =
CatetoAdyacenteaθ CatetoOpuestoaθ
SECANTE COSECANTE
Hipotenusa Hipotenusa
sec θ = csc θ =
CatetoAdyacenteaθ CatetoOpuestoaθ

4. EJEMPLO : TEOREMA DE PITÁGORAS
H
12
H2 = 122 + 35 2
θ H = 1369 = 37
35
12 12 37
senθ =
37
tan θ =
35
sec θ = 35
35 35 37
cos θ = cot θ = csc θ =
37 12 12
EJEMPLO :
Sabiendo que θ es un ángulo agudo tal que senθ=2/3.....
3 2
θ

5. PROPIEDADES DE LAS RAZONES
TRIGOMOMÉTRICAS DE ÁNGULOS AGUDOS
RAZONES TRIGONOMÉTRICAS RECÍPROCAS
1 1 1
senθ = cos θ = tan θ =
csc θ sec θ cot θ
senθ csc θ = 1 cos θ sec θ = 1 tan θ cot θ = 1
EJEMPLOS
1 1
A) = csc 36 o B) = sec17o
sen36 o cos17o
C) tan 49 o cot 49 o = 1 D)sen2θ csc 2θ = 1
E) cos 63 o sec θ = 1 θ = 63o
F) tan 2φ cot θ = 1 2φ = θ

6. PROPIEDADES DE LAS RAZONES
TRIGOMOMÉTRICAS DE ÁNGULOS AGUDOS
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS
PROPIEDAD :
“LAS RAZONES TRIGONOMÉTRICAS DE TODO ÁNGULO AGUDO
SON RESPECTIVAMENTE IGUALES A LAS CO-RAZONES
TRIGONOMÉTRICAS DE SU ÁNGULO COMPLEMENTARIO”
A LAS RAZONES TRIGONOMÉTRICAS SENO Y COSENO
TANGENTE Y COTANGENTE ;SECANTE Y COSECANTE
SE LES DENOMINA :CO-RAZONES TRIGONOMÉTRICAS
senθ = cos φ cot θ = tan φ
φ
b c cos θ = senφ sec θ = csc φ
θ tan θ = cot φ csc θ = sec φ
a

7. EJEMPLOS
A)sen25 o = cos 65 o ............... 25 o + 65 o = 90O
B) tan 43o = cot 47o ............... 43o + 47o = 90O
C) sec 60 o = csc 30o ............... 60o + 30o = 90O
D)senθ = cos 20o
θ + 20o = 90O θ = 70 o
E) tan 5α = cot α
5α + α = 90 o α = 15 o
π =
F)sen  ÷
5
cos θ
π π π π 3π
θ+ = θ= − θ= rad
5 2 2 5 10

8. TRIÁNGULOS ESPECIALES
2
)
)
1 60O 45 o 2
1
30o ( 45 o(
3 1
1
sen30 o
=
)
53 o tan 60o = 3
3 5 2
4
37o ( sec 45 = 2 cot 37 =
o o
3
4 1 3 3
tan 30o = x =
3 3 3
1 2 2
sen45 =o
x =
2 2 2

9. CALCULAR : cot θ
3 3
) 37o 4 3 3 3 45 o (
) 30o θ(
4
8
3 3
cot θ =
4

10. ÁNGULOS VERTICALES
Los ángulos verticales son ángulos agudos contenidos en
un plano vertical y formados por dos líneas imaginarias
llamadas horizontal y visual
A L
VIS U
ÁNGULO DE
)α ELEVACIÓN
HORIZONTAL
)θ
ÁNGULO DE DEPRESIÓN
VIS
U AL

11. EJEMPLO :
Una persona observa en un mismo plano vertical dos ovnis
volando a una misma altura con ángulos de elevación de
530 y 370 si la distancia entre los ovnis es de 70m ¿A qué
altura están los ovnis?
SOLUCIÓN
70
12k 12k =H
)53O )37o
9k +
16k
9k +70 = 16k k = 10 H = 120

12. ÁNGULOS HORIZONTALES
Los ángulos horizontales son ángulos agudos contenidos en
un plano horizontal, se determinan tomando como
referencia los puntos cardinales norte(N) , sur(S) , este(E) y
oeste(O).
DIRECCIÓN RUMBO
La dirección de B respecto de A El rumbo de Q respecto de P
es N30 o E o E60 o N 47o al oeste del norte
La dirección de C respecto de A El rumbo de M respecto de P
es S56 o O o O34 o S 27o al este del sur
N N
B Q
30O 47o
)
(
E O E
O A P
56 O
(
)
C 27 o
S M
S

13. EJEMPLO :
Un insecto parte de un punto F y recorre 40 km en la dirección
N530O luego recorre 402 km en la dirección SO, finalmente
recorre 60 km hacia el este. ¿A qué distancia se encuentra el
insecto de F ?
SOLUCIÓN N
OBSERVA QUE EL 45 o
TRIÁNGULO DE COLOR
ROJO ES NOTABLE 40
40 2 24
X = 20
53o
)
O
37o F E
32 x
16 16
45 o
40 20 12
60
S

14. RAZONES TRIGONOMÉTRICAS DE LA MITAD DE UN
ÁNGULO AGUDO (método gráfico)
θ (
2
c b
) θ2
θ
) 2 )θ
c + a
θ = b c−a
tan  ÷ =
2 c + a b

15. EJEMPLO :
Sabiendo que : tan 8θ=24/7, calcula tan2θ
SOLUCIÓN
24
tan 4θ =
25 + 7
25 24 tan 4 θ = 24
32
4θ 8θ 3
25 7
tan 4θ =
4
3 1
3 5 tan 2θ = tan 2θ =
9 3
4θ 2θ(
4 5