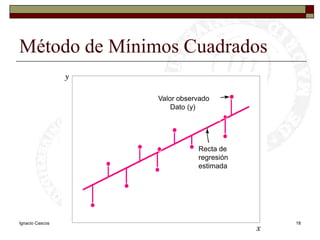
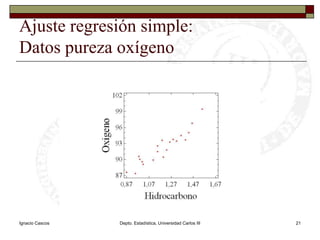
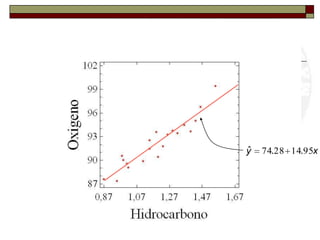
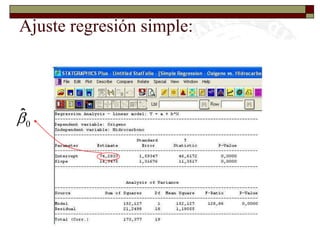
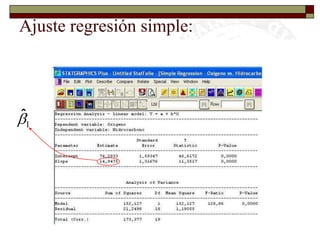
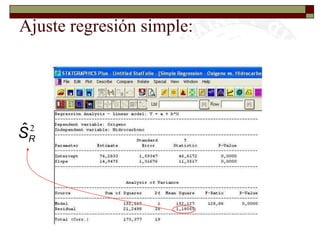
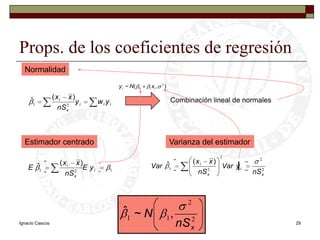
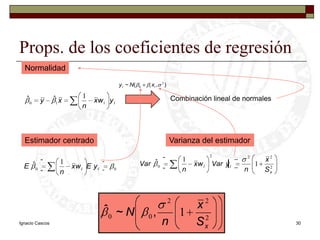
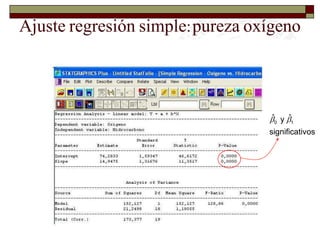
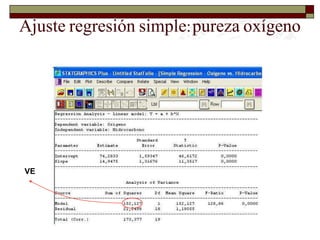
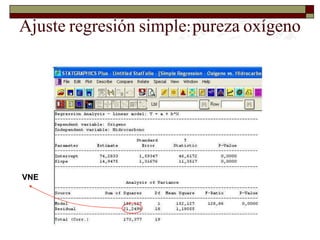
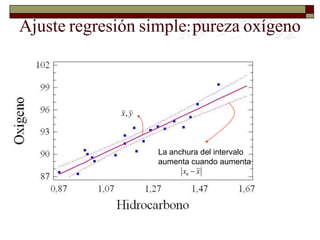
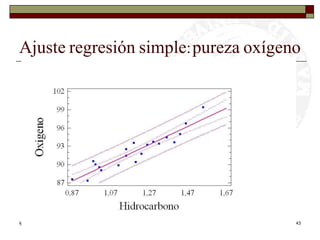
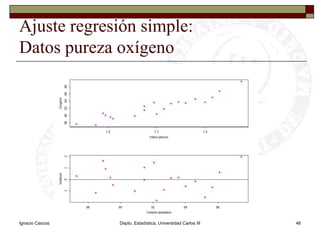
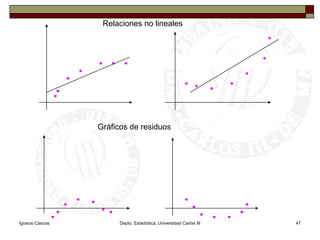
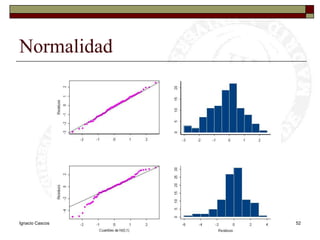
Este documento presenta una introducción al tema de la regresión lineal simple. Explica el modelo de regresión, los métodos de estimación de parámetros como mínimos cuadrados y máxima verosimilitud, e incluye información sobre inferencia, predicción y diagnóstico del modelo. El objetivo es construir y analizar modelos de regresión lineal simple.

1. Ignacio CascosDepto. Estadística, Universidad Carlos III1Regresión lineal simpleTema 1

2. Ignacio CascosDepto. Estadística, Universidad Carlos III2Descripción breve del temaIntroducciónEl modelo de regresión simpleHipótesis del modeloLinealidad, homogeneidad, homocedasticidad, independencia y normalidadEstimación de los parámetrosMínimos cuadrados, Máxima VerosimilitudPropiedades de los estimadoresCoeficientes de regresión, varianza residualInferencia y predicciónDiagnosis

3. Ignacio CascosDepto. Estadística, Universidad Carlos III3ObjetivosConstrucción de modelos de regresiónMétodos de estimación para dichos modelosInferencia acerca de los parámetrosAprendizaje de utilización de gráficos para detectar el tipo de relación entre dos variablesCuantificación del grado de relación lineal

4. Ignacio CascosDepto. Estadística, Universidad Carlos III4Descripción breve del temaIntroducciónEl modelo de regresión simpleHipótesis del modeloLinealidad, homogeneidad, homocedasticidad, independencia y normalidadEstimación de los parámetrosMínimos cuadrados, Máxima VerosimilitudPropiedades de los estimadoresCoeficientes de regresión, varianza residualInferencia y predicciónDiagnosis

5. Ignacio CascosDepto. Estadística, Universidad Carlos III5IntroducciónEstudio conjunto de dos variablesRelación entre las variablesRegresión linealHistoria del concepto de regresión lineal

6. Ignacio CascosDepto. Estadística, Universidad Carlos III6Descripción breve del temaIntroducciónEl modelo de regresión simpleHipótesis del modeloLinealidad, homogeneidad, homocedasticidad, independencia y normalidadEstimación de los parámetrosMínimos cuadrados, Máxima VerosimilitudPropiedades de los estimadoresCoeficientes de regresión, varianza residualInferencia y predicciónDiagnosis

7. Ignacio CascosDepto. Estadística, Universidad Carlos III7Ejemplo: Pureza del oxígeno en un proceso de destilación

8. Ignacio CascosDepto. Estadística, Universidad Carlos III8Ejemplo: Pureza del oxígeno en un proceso de destilación

9. Ignacio CascosDepto. Estadística, Universidad Carlos III9El modelo de regresión simplen pares de la forma (xi,yi)Objetivo: valores aproximados de Y a partir de XX: variable independiente o explicativaY: variable dependiente o respuesta (a explicar)

10. Ignacio CascosDepto. Estadística, Universidad Carlos III10El modelo de regresión simple

11. Ignacio CascosDepto. Estadística, Universidad Carlos III11Descripción breve del temaIntroducciónEl modelo de regresión simpleHipótesis del modeloLinealidad, homogeneidad, homocedasticidad, independencia y normalidadEstimación de los parámetrosMínimos cuadrados, Máxima VerosimilitudPropiedades de los estimadoresCoeficientes de regresión, varianza residualInferencia y predicciónDiagnosis

12. Ignacio CascosDepto. Estadística, Universidad Carlos III12Linealidad: datos con aspecto recto

13. Ignacio CascosDepto. Estadística, Universidad Carlos III13HomogeneidadEl valor promedio del error es cero,

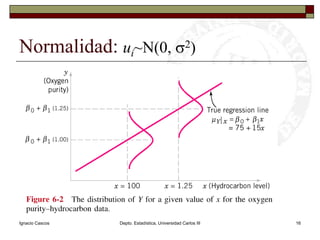
14. Ignacio CascosDepto. Estadística, Universidad Carlos III14Homocedasticidad:Var[ui]=s2 Varianza de errores constante

15. Ignacio CascosDepto. Estadística, Universidad Carlos III15Independencia: Observaciones independientes, en particular E[uiuj]= 0

16. Ignacio CascosDepto. Estadística, Universidad Carlos III16Normalidad: ui~N(0, s2)

17. Ignacio CascosDepto. Estadística, Universidad Carlos III17Descripción breve del temaIntroducciónEl modelo de regresión simpleHipótesis del modeloLinealidad, homogeneidad, homocedasticidad, independencia y normalidadEstimación de los parámetrosMínimos cuadrados, Máxima VerosimilitudPropiedades de los estimadoresCoeficientes de regresión, varianza residualInferencia y predicciónTansformaciones

18. Ignacio CascosDepto. Estadística, Universidad Carlos III18Método de Mínimos CuadradosValor observado Dato (y)Valor observado Dato (y)Recta de regresiónestimadaRecta de regresiónestimada

19. Ignacio CascosDepto. Estadística, Universidad Carlos III19Mínimos Cuadrados (Gauss, 1809)Objetivo: Buscar los valores de b0 y b1 que mejor se ajustan a nuestros datos.Ecuación:Residuo:Minimizar:

20. Ignacio CascosDepto. Estadística, Universidad Carlos III20Mínimos Cuadrados (Gauss, 1809)Resultado:

21. Ignacio CascosDepto. Estadística, Universidad Carlos III21Ajuste regresión simple:Datos pureza oxígeno

22. Ignacio CascosDepto. Estadística, Universidad Carlos III22Ajuste regresión simple:Datos pureza oxígeno

23. Ignacio CascosDepto. Estadística, Universidad Carlos III23Ajuste regresión simple:Datos pureza oxígeno

24. Ignacio CascosDepto. Estadística, Universidad Carlos III24Ajuste regresión simple:Datos pureza oxígeno

25. Ignacio CascosDepto. Estadística, Universidad Carlos III25Ajuste regresión simple:Datos pureza oxígeno

26. Ignacio CascosDepto. Estadística, Universidad Carlos III26Método de Máxima VerosimilitudMismo resultado.Estimación de la varianza:

27. Ignacio CascosDepto. Estadística, Universidad Carlos III27Ajuste regresión simple:Datos pureza oxígeno

28. Ignacio CascosDepto. Estadística, Universidad Carlos III28Descripción breve del temaIntroducciónEl modelo de regresión simpleHipótesis del modeloLinealidad, homogeneidad, homocedasticidad, independencia y normalidadEstimación de los parámetrosMínimos cuadrados, Máxima VerosimilitudPropiedades de los estimadoresCoeficientes de regresión, varianza residualInferencia y predicciónDiagnosis

29. Ignacio CascosDepto. Estadística, Universidad Carlos III29Props. de los coeficientes de regresiónNormalidad Combinación lineal de normalesEstimador centradoVarianza del estimador

30. Ignacio CascosDepto. Estadística, Universidad Carlos III30Props. de los coeficientes de regresiónNormalidad Combinación lineal de normalesEstimador centradoVarianza del estimador

31. Ignacio CascosDepto. Estadística, Universidad Carlos III31Descripción breve del temaIntroducciónEl modelo de regresión simpleHipótesis del modeloLinealidad, homogeneidad, homocedasticidad, independencia y normalidadEstimación de los parámetrosMínimos cuadrados, Máxima VerosimilitudPropiedades de los estimadoresCoeficientes de regresión, varianza residualInferencia y predicciónDiagnosis

32. Ignacio CascosDepto. Estadística, Universidad Carlos III32Inferencia respecto a los parámetros IC

33. Ignacio CascosDepto. Estadística, Universidad Carlos III33Inferencia respecto a los parámetrosContraste de Hipótesis

34. Ignacio CascosDepto. Estadística, Universidad Carlos III34Ajusteregresiónsimple:purezaoxígeno

35. Ignacio CascosDepto. Estadística, Universidad Carlos III35Descomposición de la variabilidad La variabilidad del modelo satisface: VT =VE+VNEContraste de regresión

36. Ignacio CascosDepto. Estadística, Universidad Carlos III36Ajusteregresiónsimple:purezaoxígenoVE

37. Ignacio CascosDepto. Estadística, Universidad Carlos III37Ajusteregresiónsimple:purezaoxígenoVNE

38. Ignacio CascosDepto. Estadística, Universidad Carlos III38Coeficiente de determinación

39. Ignacio CascosDepto. Estadística, Universidad Carlos III39Predicción Dos tipos de predicción:Predecir un valor promedio de y para cierto valor de x.Predecir futuros valores de la variable respuesta.La predicción es la misma (a partir de la recta de regresión) pero la precisión de los estimadores es diferente.

40. Ignacio CascosDepto. Estadística, Universidad Carlos III40Predicción (promedio) Estimación de la media de la distribución condicionada de y para x=x0:Intervalo de confianza para la media estimada

41. Ignacio CascosDepto. Estadística, Universidad Carlos III41Ajusteregresiónsimple:purezaoxígenoLa anchura del intervaloaumenta cuando aumenta

42. Ignacio CascosDepto. Estadística, Universidad Carlos III42Predicción para futuros valores Intervalo de predicción

43. Ignacio CascosDepto. Estadística, Universidad Carlos III43Ajusteregresiónsimple:purezaoxígeno

44. Ignacio CascosDepto. Estadística, Universidad Carlos III44Descripción breve del temaIntroducciónEl modelo de regresión simpleHipótesis del modeloLinealidad, homogeneidad, homocedasticidad, independencia y normalidadEstimación de los parámetrosMínimos cuadrados, Máxima VerosimilitudPropiedades de los estimadoresCoeficientes de regresión, varianza residualInferencia y predicciónDiagnosis

45. Ignacio CascosDepto. Estadística, Universidad Carlos III45DiagnosisUna vez ajustado el modelo, hay que comprobar si se cumplen las hipótesis iniciales.Gráficos de residuos frente a valores previstos.Si las hipótesis iniciales se satisfacen, este gráfico no debe tener estructura alguna.

46. Ignacio CascosDepto. Estadística, Universidad Carlos III46Ajuste regresión simple:Datos pureza oxígeno

47. Ignacio CascosDepto. Estadística, Universidad Carlos III47Relaciones no linealesGráficos de residuos

48. Ignacio CascosDepto. Estadística, Universidad Carlos III48LinealidadSoluciones a la falta de linealidad:Transformar las variables para intentar conseguir linealidad. Introducir variable adicionales.Detectar la presencia de datos atípicos o ausencia de otras variables importantes para explicar la variable respuesta.

49. Ignacio CascosDepto. Estadística, Universidad Carlos III49HomocedasticidadCuando la varianza de las perturbaciones es muy diferente para unos valores de la variable explicativa que para otros tenemos heterocedasticidade.^y

50. Ignacio CascosDepto. Estadística, Universidad Carlos III50HomocedasticidadSoluciones a la heterocedasticidad:Si la variabilidad de la respuesta aumenta con xsegún la ecuación Var(y|x) = g(x), dividimos la ecuación de regresión (y) entre g(x).Transformar la variable respuesta y puede que también x.Si lo anterior no funciona, cambiar el método de estimación.

51. Ignacio CascosDepto. Estadística, Universidad Carlos III51NormalidadLa falta de normalidad invalida resultados inferenciales.Comprobación mediante histogramas o gráficos probabilísticos.En un gráfico probabilístico comparamos los residuos ordenados con los cuantiles de la distribución Normal estándar.Si la distribución de los residuos es normal, el gráfico ha de mostrar aproximadamente una recta.

52. Ignacio CascosDepto. Estadística, Universidad Carlos III52Normalidad

53. Ignacio CascosDepto. Estadística, Universidad Carlos III53Independencia y Datos influyentesIndependenciaConviene hacer una gráfica de residuos frente a tiempo (residuos incorrelados).Datos influyentesAnalizar la presencia de datos influyentes. Los atípicos son datos muy grandes o muy pequeños. Estudiar su posible eliminación.

54. Ignacio CascosDepto. Estadística, Universidad Carlos III54Transformaciones