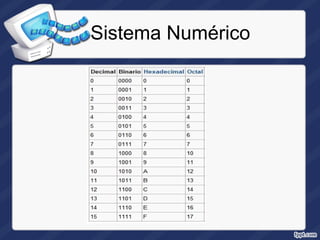
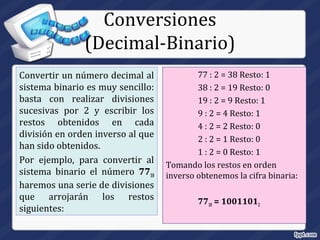
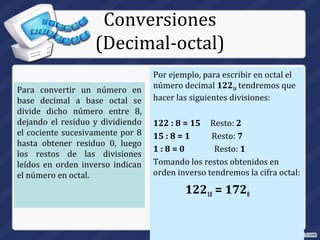
El documento resume los principales sistemas numéricos utilizados en computación, incluyendo el binario, decimal, hexadecimal y octal. Explica que el sistema binario es la base de cómo las computadoras representan y procesan datos internamente debido a que sus componentes sólo pueden estar en dos estados. También describe cómo realizar conversiones entre estos sistemas numéricos, como convertir de decimal a binario, hexadecimal u octal y viceversa.

1. Representación de la
Información en la
computadora
Tecnología Información y
Comunicación.
Realizado por: Yamileth Rivera
Profesor: Martin Arosemena

2. Sistema Numérico
El estudio de las computadoras y del procesamiento
de datos requiere algún conocimiento de los
sistemas numéricos, ya que éstos constituyen la base
de todas las transformaciones de información que
ocurren en el interior de la computadora.

3.  El sistema binario, compuesto por los símbolos 1 y 0, es el que utiliza la computadora en su
funcionamiento interno. La computadora opera en binario debido a que sus componentes
físicos, pueden representar solamente dos estados de condición: apagado/prendido,
abierto/cerrado, magnetizado/no magnetizado, etc. Estados de condición a los que se les asigna
el valor 1 ó 0.
 El sistema decimal, compuesto por los símbolos 0 al 9, es el sistema numérico que
utilizamos a diario.
 El sistema hexadecimal, con 16 símbolos, ofrece la posibilidad de comprimir los números
binarios para hacerlos más sencillos de tratar.
Sistema Numérico

4. Sistema decimal
El más importante factor en el
desarrollo de la ciencia y la matemática
fue la invención del sistema decimal de
numeración. Este sistema utiliza diez
símbolos: 0,1,2,3,4,5,6,7,8,9,
denominados generalmente "cifras
decimales". La costumbre de contar por
decenas se originó probablemente en el
hecho de tener el hombre diez dedos.

5. Sistema binario
El sistema numérico binario (de
base 2) usa solamente dos
símbolos diferentes, 0 y 1, que
significan "ninguna unidad" y
"una unidad" respectivamente. A
diferencia del sistema decimal, el
valor relativo de los dígitos
binarios a la izquierda del dígito
menos significativo aumenta en
una potencia de dos cada vez, en
lugar de hacerlo en potencias de
diez.

6. Representación binaria

7. Sistema hexadecimal
Los números binarios de gran magnitud consisten en largas series de
ceros y unos, que son difíciles de interpretar y manejar. Como un medio
conveniente para representar esos números binarios de gran magnitud se
utiliza el sistema numérico hexadecimal (de base 16). Cada dígito
hexadecimal representa cuatro dígitos binarios.
La notación hexadecimal requiere el uso de 16 símbolos para representar
16 valores numéricos. Dado que el sistema decimal proporciona
solamente diez símbolos numéricos (de 0 a 9), se necesitan seis símbolos
adicionales para representar los valores restantes. Se han adoptado para
este fin las letras A, B, C, D, E, y F aunque podrían haberse utilizado
cualesquiera otros símbolos. La lista completa de símbolos hexadecimales
consta, por lo tanto, del 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F, en orden
ascendente de valor.

8. Representación
Hexadecimal
Por ejemplo el número Hexadecimal 3E0A16 significa
(reemplazando los símbolos hexadecimales con símbolos
decimales)
3×163
+ E×162
+ 0×161
+ A×160
= 3×4096 + 14×256 + 0×16 + 10×1
= 15882.

9. Sistema octal
El sistema numérico en base 8 se llama octal y
utiliza los dígitos del 0 al 7.
En informática a veces se utiliza la numeración
octal en vez de la hexadecimal. Tiene la ventaja de
que no requiere utilizar otros símbolos diferentes
de los dígitos. Sin embargo, para trabajar con bytes
o conjuntos de ellos, asumiendo que un byte es una
palabra de 8 bits, suele ser más cómodo el sistema
hexadecimal, por cuanto todo byte así definido es
completamente representable por dos dígitos
hexadecimales.

10. Representación Octal
En el sistema de numeración octal, los números se representan
mediante ocho dígitos diferentes: 0, 1, 2, 3, 4, 5, 6 y 7. Cada dígito
tiene, naturalmente, un valor distinto dependiendo del lu­gar que
ocupen. El valor de cada una de las posiciones viene determinado por
las potencias de base 8.
Por ejemplo, el número octal 2738 tiene un valor decimal:
2*83
+ 7*82
+ 3*81
= 2*512 + 7*64 + 3*8 = 149610
2738 = 149610

11. Sistema Numérico

12. Conversiones
(Decimal-Binario)
Convertir un número decimal al
sistema binario es muy sencillo:
basta con realizar divisiones
sucesivas por 2 y escribir los
restos obtenidos en cada
división en orden inverso al que
han sido obtenidos.
Por ejemplo, para convertir al
sistema binario el número 7710
haremos una serie de divisiones
que arrojarán los restos
siguientes:
77 : 2 = 38 Resto: 1
38 : 2 = 19 Resto: 0
19 : 2 = 9 Resto: 1
9 : 2 = 4 Resto: 1
4 : 2 = 2 Resto: 0
2 : 2 = 1 Resto: 0
1 : 2 = 0 Resto: 1
Tomando los restos en orden
inverso obtenemos la cifra binaria:
7710 = 10011012

13. La primera forma la haremos a base de dividir el número decimal entre 16, hasta
que no podamos dividir más.
1869 / 16 = 116 Resto 13 equivale a la letra D
116 / 16 = 7 Resto 4 su equivalente es el 4
Como el último cociente no es divisible entre 16, este pasa a formar parte del
número que se forma en la notación hexadecimal.
Para formar el número en notación hexadecimal procedemos de la siguiente
manera, el primer número hexadecimal es el cociente de la última división (7) y
seguidamente en orden ascendente se van colocando los restos hacia la izquierda,
para formar el número en hexadecimal (74D16).
= 74D16
Conversiones
(Decimal-Hexadecimal)
Hay varios métodos, para realizar la conversión de decimal a hexadecimal, en esta
oportunidad explicaremos dos (2) formas para realizarlo.

14. Conversiones
(Decimal-Hexadecimal)
Ejemplo el numero 423

15. Esta forma es más sencilla que la
anterior y consiste en pasar el número
decimal a binario y después convertirlo
a hexadecimal.
Tomemos el mismo ejemplo de la
primera forma.
186910 su equivalente en binario es
111010011012.
Para pasar de un número binario a
hexadecimal debemos hacer
agrupaciones de 4 bits, tomando el
punto de inicio el último número
binario de la derecha.
Iremos haciendo agrupaciones de
derecha a izquierda
Primer grupo 1101 corresponde a D
(13) en hexadecimal.
Segundo grupo 0100 corresponde a 4
en hexadecimal.
Tercer grupo 0111 corresponde a 7 en
hexadecimal.
El resultado de 0111010011012 es
74D16 cuyo valor decimal es 186910
Conversiones
(Decimal-Hexadecimal)

16. Para convertir un número en
base decimal a base octal se
divide dicho número entre 8,
dejando el residuo y dividiendo
el cociente sucesivamente por 8
hasta obtener residuo 0, luego
los restos de las divisiones
leídos en orden inverso indican
el número en octal.
Por ejemplo, para escribir en octal el
número decimal 12210 tendremos que
hacer las siguientes divisiones:
122 : 8 = 15 Resto: 2
15 : 8 = 1 Resto: 7
1 : 8 = 0 Resto: 1
Tomando los restos obtenidos en
orden inverso tendremos la cifra octal:
12210 = 1728
Conversiones
(Decimal-octal)

17. Para realizar la conversión de binario a decimal, realice lo siguiente:
Comience por el lado derecho del número en binario.
Multiplique cada dígito por 2 elevado a la potencia consecutiva (comenzando
por la potencia 0, 20
).
Después de realizar cada una de las multiplicaciones.
Súmelas todas y el número resultante será el equivalente al sistema decimal.
Ejemplos: (Los números de arriba indican la potencia a la que hay que elevar 2)
Conversiones
(Binario-decimal)

18. Se divide el número binario en
grupos de cuatro dígitos binarios,
comenzando desde la derecha y se
reemplaza cada grupo por el
correspondiente símbolo
hexadecimal. Si el grupo de la
extrema izquierda no tiene cuatro
dígitos, se deben agregar ceros
hasta completar 4 dígitos.
Conversiones
(Binario-Hexadecimal)
Ejemplo: (111110011011010011)2
= 0011 / 1110 / 0110 / 1101 /
0011
= 3 E 6 D 3
= (3E6D3)16
Otro ejemplo:
(101110)2
= 0010 / 11102
= 2E16

19. MUCHAS GRACIAS