Este documento presenta conceptos básicos de lógica proposicional para apoyar a estudiantes de ingeniería civil. Define proposiciones, funciones proposicionales, operaciones lógicas como negación, conjunción, disyunción, implicación y doble implicación. Explica sus tablas de verdad y provee ejemplos para ilustrar cada concepto. El objetivo es integrar estas herramientas lógicas en la resolución de problemas matemáticos relevantes para la carrera.

1. 1
Universidad Nacional de Formosa
Facultad de Recursos Naturales
Material de Apoyo para ingresantes a Ingeniería civil
“Estrategias de Aprendizaje para un Modelo Integrador”
MATEMÁTICA
Zulma Elizabeth Zamudio de Paredes
Azucena González de Ortiz
Juan Carlos Barreto
Gustavo Daniel Medina
Año 2018

2. 2
Índice
Introducción 3
Lógica Propocional 4
Conjuntos Numéricos 18
Expresiones Algebraicas 28
Razones y proporciones 48
Trigonometría 55
Vectores 67
Funciones 82
Ecuaciones 111
Sistemas de Ecuaciones 119
Geometría y Resolución de problemas 126
Aplicaciones de GeoGebra en la Resolución de Problemas 129

3. 3
Introducción
El presente material está pensado para acompañar a los estudiantes que ingresan a la
carrera de Ingeniería Civil con una propuesta integradora.
A continuación se detallan algunos aspectos:
Metodología de Evaluación: se realiza una evaluación permanente de los logros de los
estudiantes. La evaluación continua se realiza a través de los trabajos prácticos
individuales y grupales. Además los alumnos acceden a mini parciales cada dos
semanas que les posibilita promocionar el curso introductorio con la cumplimentación
de las actividades propuesta en el taller de epistemología de las ciencias e informática.
Integración de las TIC en matemática y física: en las actividades prácticas de
matemática y física se ha incorporado el uso de GeoGebra como programa dinámico
que les permite comprender mejor los conceptos y propiedades.
Aplicaciónes de la física y la matemática a situaciones problemáticas. Se
incorporaron problemas reales más cercanos al área en estudio.

4. 4
LÓGICA PROPOCIONAL
Proposición
Una proposición es todo enunciado al que se le puede asignar uno y sólo uno de los
valores de verdad, que son:
VERDADERO (V) o FALSO (F)
Por lo general, las proposiciones se representan con las letras minúsculas del alfabeto, desde la
letra p en adelante, es decir, p, q, r, s, t, ... etc.
Ejemplo
a) La expresión 15 + 5 = 21 es una proposición que se puede indicar brevemente de la forma
p: 15 + 5 = 21
cuyo valor de verdad es falso, lo que se indica mediante
V(p) = F
b) Sea la proposición
q: Santa Fe es una provincia argentina V(q) = V
c) Sea la proposición
r: el número 15 es divisible por 3 V(r) = V
Funciones Proposiciones
Si en la proposición "cinco es mayor que tres" (en símbolos es 5 > 3) reemplazamos al
número 5 por la letra x, se obtiene la expresión "x es mayor que tres" (x > 3), y si
convenimos que x no represente necesariamente al número 5, sino a un número real
cualquiera, entonces el enunciado x > 3 se denomina función proposicional y se anota
p(x) o p(x).
Una función proposicional en una variable o indeterminada x es un enunciado en el que
aparece x como sujeto y que se convierte en una proposición cuando se le asigna un valor
específico a la variable.
Ejemplo
Sea la función proposicional p(x): 2x-5 = 3. Si se remplaza x por 4 y x por 2, se obtienen,
respectivamente, los siguientes valores de verdad: p(4) = V y p(2) = F
Ejemplos
p(x): 2x + 5 > 11. Si x = 4, p(4) = 13  13 > 11 (Verdadero)
q(y): 3y + 7 = 11. Si y = 5, q(5) = 22  22 = 16 (Falso)

5. 5
r(x): 2x + 1 = 5. Si x = 2, r(2) = 5  5 = 5 (Verdadero)
Observación
Las proposiciones pueden ser simples o compuestas, estas últimas constan de dos o más
enunciados simples.
Ejemplo
Sea la siguiente proposición r
r: Pitágoras era griego y era geómetra.
p y q
Se observan dos proposiciones simples. La primera, p, nos afirma que Pitágoras era griego y la
segunda, q, que Pitágoras era geómetra.
Operaciones Lógicas
A partir de proposiciones simples es posible generar otras, las compuestas. Es decir, se
puede operar con proposiciones utilizando para ello ciertos símbolos llamados
conectivos lógicos.
Operación Símbolo Significado
Negación
Conjunción o producto lógico
Disyunción o suma lógica
Implicación
Doble implicación
Diferencia simétrica o Disyunción excluyente
~





“no …..” o “no es cierto que …
“…. y ….”
“… o …” (en sentido incluyente)
“… implica …”, o “si… entonces …”
“… si y sólo si …”
“ … o …” (en sentido excluyente)
Negación
Dada una proposición p, se denomina negación de p a otra proposición denotada por ~p (se
lee "no p") que le asigna el valor veritativo opuesto al de p. Esta ley que define a la negación
lógica o simplemente negación, se presenta generalmente, en forma resumida utilizando una
tabla de doble entrada denominada tabla de verdad.
La tabla de verdad de la negación es:

6. 6
p ~p
V
F
F
V
Ejemplo
Sea la proposición p: 3 > 1, su negación es ~ p: 3 ≤ 1.
Se observa que V(p) = V y V(~ p) = F
NOTA: se trata de una operación unitaria, pues se define para una proposición.
Conjunción o Producto Lógico
Dadas dos proposiciones p y q, se denomina conjunción de estas proposiciones a la
proposición compuesta p  q (se lee "p y q"), cuya tabla de verdad es:
p q p  q
V
V
F
F
V
F
V
F
V
F
F
F
La tabla que define esta operación, establece que la conjunción es verdadera sólo si lo son las
dos proposiciones componentes (en todo otro caso, es falsa). Es una operación binaria.
Ejemplos
a) Sean las proposiciones
p: 5 es un número impar
q: 6 es un número par
Entonces la conjunción entre p y q es
p  q: 5 es un número impar y 6 es un número par
Se obtienen los siguientes valores de verdad:
Observamos que al valor V de p,
la negación le hace corresponder
el valor F, y viceversa.

7. 7
V(p  q) = V
V(~p  q) = F
b) Sean las proposiciones
r: todos los número pares son divisibles por 2
~ r: existe un número par que no es divisible por 2
¿Qué valor de verdad tiene la proposición compuesta r  ~ r?
Cualquiera sea la proposición p ¿qué valor de verdad tiene p  ~ p?
Disyunción o Suma lógica
Dadas dos proposiciones p y q, la disyunción de las proposiciones p y q es la proposición p  q
(se lee “p o q”) cuya tabla de valores de verdad es:
p q p  q
V
V
F
F
V
F
V
F
V
V
V
F
La disyunción o es utilizada en sentido incluyente, ya que la verdad de la disyunción se da en
el caso de que al menos una de las proposiciones sea verdadera. En el lenguaje ordinario la
palabra o es utilizada en sentido incluyente o excluyente indistintamente. Para evitar toda
posibilidad de ambigüedades, en matemática se utiliza la disyunción definida por la tabla
precedente, que muestra que la disyunción sólo es falsa cuando ambas proposiciones son
falsas, o bien, se utiliza la disyunción excluyente para interpretar otra situación.
Ejemplo
Sean las proposiciones
p: 5 es un número impar y q: 6 es un número par
La proposición compuesta que indica la disyunción entre p y q es
p  q: 5 es un número impar o 6 es un número par

8. 8
El valor de verdad del enunciado compuesto anterior es
V(p  q) = V
El valor de verdad del enunciado compuesto ~ p  ~ q es V(~p  ~q) = F
Implicación o Condicional
Implicación de las proposiciones p y q es la proposición p  q (si p entonces q) cuya tabla de
valores de verdad es:
p q p  q
V
V
F
F
V
F
V
F
V
F
V
V
La proposición p se llama antecedente, y la proposición q se llama consecuente de la
implicación o condicional. La tabla nos muestra que la implicación sólo es falsa si el
antecedente es verdadero y el consecuente es falso.
Sean las proposiciones
p: José es mendocino y q: José es argentino
La proposición compuesta p implica q es
p  q: Si José es mendocino, José es Argentino
V(p  q)= V
V(p  ~q)= F
V(q  p)= F
Expresiones sinónimas
p  q
Si p entonces q
Si p, q
Todo p verifica q
p implica q
p sólo si q

9. 9
q si p
q cuando p
Si además V( p  q ) =V, se dice que
p es condición suficiente para q y q es condición necesaria para p
Ejemplo
a) Sean las funciones proposicionales
r (x): x > 2
s (x): x2
> 4
El enunciado si x > 2 entonces x2
> 4, es una proposición verdadera, por lo cual r es condición
suficiente para s, y s es condición necesaria para r.
El enunciado si x2
> 4 entonces x > 2, es una proposición falsa, por lo cual s no es condición
suficiente para r, y r es condición necesaria para s.
b) Sea la función proposicional 2x + 5 ≥ 13, ¿Es x ≥ 0 una condición necesaria, suficiente, o
necesaria y suficiente para que la proposición sea verdadera?
c) La siguiente implicación es verdadera:
"Si el triángulo T es equilátero, entonces T es isósceles"
En este caso, se tienen las proposiciones
p: T es triángulo equilátero y
q: T es triángulo isósceles
La proposición p es condición suficiente para q, es decir, que un triángulo sea equilátero es
suficiente para asegurar que es isósceles. Por otra parte, T es equilátero sólo si es isósceles; es
decir que un triángulo sea isósceles es necesario para que sea equilátero.
Implicaciones asociadas

10. 10
Dada la implicación p  q, que llamaremos directa, existen varias implicaciones asociadas, una
de ellas es la implicación contrarrecíproca ~q  ~p. Haciendo la tabla de verdad
p q p  q ~p ~q ~q  ~p
V
V
F
F
V
F
V
F
V
F
V
V
F
F
V
V
F
V
F
V
V
F
V
V
se observa que los valores de verdad de las implicaciones p  q y ~q  ~p son iguales. Se
dice que las implicaciones contrarrecíprocas son equivalentes, es decir, tienen el mismo valor
de verdad.
¿Cómo son los valores de verdad de la implicación p  q y de la denominada implicación
recíproca q  p?
Doble Implicación o Bicondicional
Doble implicación de las proposiciones p y q es la proposición p  q (se lee "p si y sólo si q")
cuya tabla de valores de verdad es
p q p  q
V
V
F
F
V
F
V
F
V
F
F
V
La doble implicación o bicondicional sólo es verdadera si ambas proposiciones tienen el mismo
valor de verdad.

11. 11
La doble implicación puede definirse como la conjunción de una implicación y su recíproca. De
este modo, la tabla de valores de verdad de p  q puede obtenerse mediante la tabla de (p
 q)  (q  p), como vemos:
p q p  q q  p (p  q)  (q  p)
V
V
F
F
V
F
V
F
V
F
V
V
V
V
F
V
V
F
F
V
Ejemplo
Sea el enunciado
a = b si y sólo si a² = b²
donde a y b son números reales cualesquiera.
Se observa que el enunciado está compuesto por las proposiciones:
p: a = b y q: a² = b²
Como V(p  q) =V y V(q  p) = F, entonces V(p  q) = F
OBSERVACIÓN
La doble implicación p  q, es una operación equivalente a la conjunción de las implicaciones
(p  q)  (q  p)
Si V(p  q) = V, entonces V(p  q) = V y V(q  p) = V. Se tiene, observando el valor de verdad
de la primera implicación, que p es condición suficiente para q y, teniendo en cuenta la
segunda implicación, ocurre que p es condición necesaria para q.
Es decir, si V(p  q) = V, entonces p es condición necesaria y suficiente para q y,
análogamente, q es también condición necesaria y suficiente para p.

12. 12
Proposiciones lógicamente equivalentes
Dos proposiciones p y q se llaman equivalentes si sus tablas de verdad son idénticas. De
ser así se denota: p  q
Ejemplo
Sea la proposición compuesta p  q, recordamos su tabla de verdad
p q p  q
V
V
F
F
V
F
V
F
V
F
V
V
Ahora bien, si analizamos la proposición compuesta ~p  q, su tabla de verdad es
p ~p q ~p  q
V
V
F
F
F
F
V
V
V
F
V
F
V
F
V
V
Se observa que las tablas de valores de verdad de ambas proposiciones son iguales. Se dice
que ambas proposiciones son lógicamente equivalentes, y en este caso particular lo
simbolizamos:
(p  q)  (~p  q)

13. 13
Clasificación de proposiciones: Tautología, contradicción y
contingencia
Al conjunto de proposiciones, conectivos lógicos y símbolos de agrupación lo denominamos
fórmula lógica.
Por ejemplo,
~ { (p  q)  (s  t) }
Si al evaluar una fórmula lógica, resulta que todos los valores de verdad son siempre
verdaderos para cualquier combinación de los valores de verdad de las proposiciones
componentes, se dice que dicha fórmula es una Tautología o Ley lógica.
Ejemplo
Analizando la proposición p  ~p mediante la tabla de verdad, se tiene:
p ~p p  ~p
V
F
F
V
V
V
Se observa que para cualquier combinación de las proposiciones p y su negación ~p, la
proposición p  ~p es siempre verdadera. Luego, la proposición compuesta p  ~p es una
tautología.
Ejemplo
Sea la fórmula lógica { ( p  q )  p }  q
La tabla de valores de verdad es:
p q p  q { ( p  q )  p }  q
V
V
F
V
F
V
V
F
V
V
F
F
V
V
V
F
V

14. 14
F F V F V
V
F
Se observa que, independientemente de la combinación de valores de verdad de las
proposiciones p y q, el resultado de la fórmula lógica es siempre verdadero. Esta fórmula es
una tautología.
Si al estudiar una fórmula lógica, a diferencia de los ejemplos anteriores resulta que para
cualquier valor de verdad de las proposiciones intervinientes el resultado de dicha fórmula es
siempre falso, se dice que dicha fórmula es una Contradicción.
Ejemplo
Analicemos la fórmula lógica p  ~p
p ~p p  ~p
V
F
F
V
F
F
La fórmula es siempre falsa, es una Contradicción.
NOTA: Si una proposición no es una tautología ni una contradicción (es decir que contiene al
menos un valor V y otro F) es una Contingencia.
Cuantificación de las Funciones Proposicionales
Cuantificadores
A partir de funciones proposicionales es posible obtener proposiciones generales mediante un
proceso llamado de cuantificación. Asociados a la indeterminada x, introducimos los símbolos
“x” y “x”, llamados cuantificador universal y cuantificador existencial, respectivamente.
Las expresiones

15. 15
“para todo x, se verifica p(x) ” se denota en símbolos por  x :
p(x)
”existe x, tal que se verifica p(x)” se denota en símbolos por  x : p(x)
corresponden a una función proposicional p(x) cuantificada universalmente en el primer caso, y
existencialmente en el segundo.
Una función proposicional cuantificada universalmente es V si y sólo si son V todas las
proposiciones particulares asociadas a ella. Para asegurar la verdad de una proposición
cuantificada existencialmente es suficiente que sea verdadera alguna de las proposiciones
asociadas a la función proposicional.
Ejemplos
a) Todo número natural es entero.
b) Existen números enteros que son naturales.
c) Todo número entero es racional
d) Existen números irracionales que son naturales
Negación de funciones proposicionales cuantificadas
Un problema de interés, no sólo en Matemática, sino en las restantes ciencias, es la negación
de funciones proposicionales cuantificadas. Por ejemplo, la negación de
"Todos los enteros son impares" ( x : p(x))
es
"Existen enteros que no son impares" ( x / ~p(x))
Luego, para negar una función proposicional cuantificada universalmente se cambia el
cuantificador en existencial y se niega la función proposicional.¿Cómo se niega una función
proposicional cuantificada existencialmente?
Demostración Matemática
Todo teorema matemático se puede formular como una implicación
p  q
Hipótesis Tesis
Premisa Conclusión

16. 16
Esta implicación puede ser V o F.
En el caso de ser falsa, basta con un contraejemplo para refutarla. En el caso de ser verdadera,
hay que realizar una demostración.
Refutación
V(p  q) = F, sólo sucede en el caso de que V(p) =V y V(q) = F, por lo que
V(p ~ q) = V, razón por la cual, para dar un contraejemplo, se debe verificar que
V(p ~ q) = V
Ejemplo
Sea el enunciado “si x (natural) es un número impar, entonces es múltiplo de 3”.
Como la implicación es falsa, para refutarla, hay que buscar un número que sea impar pero
que no sea múltiplo de 3, por ejemplo 7.
Demostración
Para realizar una demostración, se usan los llamados métodos directos o indirectos.
Método directo: a partir de la verdad de p se debe concluir en la verdad de q.
Método Directo
p  q
q
Verdadera Falsa
Contraejemplo
Demostración
Métodos Indirectos
Contrarrecíproco Contradicción

17. 17
Ejemplo
Sea el enunciado “si n es un número par entonces n.m es par para todo número entero m”.
Demostración
Si n es un número par, n se puede escribir de la forma 2.k, siendo k un número entero, es decir
n = 2.k, luego m.n = m.(2.k)
= 2.(m.k)
= 2. t
Luego m.n es par ya que puede escribirse como 2.t, siendo t un número entero.
Métodos indirectos:
I) Se utiliza la implicación contrarrecíproca, es decir, demostrar la verdad de p  q es
equivalente a mostrar la verdad de ~q  ~p.
Ejemplo
Sea la implicación directa “siendo n entero, si n2
es par entonces n es par”
La implicación contrarrecíproca es “siendo n entero, si n es impar entonces n2
es impar”
Demostrando la verdad del enunciado contrarrecíproco se demuestra la verdad de la
implicación directa.
Demostración
Si n es impar, puede escribirse de la forma n = 2k+1, siendo k un número entero, luego
n2
= (2k + 1)2
= 4 k2
+ 4k + 12
= 2 (2 k2
+ 2k) + 1, que es un número impar, luego, si n2
es
par entonces n es par.
II) Por contradicción, como V(p  q) = V, y se sabe por hipótesis que V(p) =V y se debe concluir
que V(q) =V, entonces V(p ~ q) = F o una contradicción.
Ejemplo
Probar que el opuesto de un número real es único.

18. 18
Conjuntos Numéricos
Símbolos Matemáticos de uso frecuente
Algunas letras del alfabeto griego
Objetivos
irracional, entre real y complejo

19. 19
Números Reales
Conjuntos Numéricos y Propiedades
Los números naturales son los números que utilizamos para contar, estos son:
{1,2,3,4,5,6,7,8, …}. Los puntos suspensivos indican que los números continúan de esa
forma, sin terminar nunca.
Si sumamos dos números naturales obtenemos otro número natural, por ejemplo:
8 + 5 = 13. Pero si restamos 5 – 5 , necesitamos otro número que represente el resultado.
Ese número es cero. Este conjunto es el conjunto de los números cardinales
{0,1,2,3,4,5,6,7,8,…}.
En el diario vivir se escuchan expresiones como: “ 10 grado bajo cero”, 647 en
débito”, “8 pies bajo el nivel del mar”. Estas tres expresiones se refieren a números
menores que cero. Con estas situaciones surgen los enteros negativos. Los enteros
negativos, el cero y los números naturales (también conocidos por enteros positivos)
forman el conjunto de los números enteros, estos son {…,-4,-3,-2,-1,0,1,2,3,4,…}.
Si sumamos, restamos y multiplicamos enteros siempre se obtiene otro número
entero. Pero si dividimos dos enteros no siempre obtendremos otro entero. Por ejemplo,
16 ÷ 2 = 8 pero en 3 ÷ 4 el resultado no es un entero. Existen muchas divisiones donde
el resultado no es un entero. Esta situación nos lleva a otro conjunto numérico conocido
por los números racionales.
Los números racionales son todos aquellos números que se pueden escribir de
la forma donde b es diferente de cero. Los números naturales, los cardinales y los
enteros son números racionales. Otros ejemplos de números racionales son:
Existe otro conjunto de números que son los números irracionales, estos son
números que no son racionales, esto es, que no se pueden expresar de la forma
a
b
donde
b es diferente de cero. Ejemplos: √2 = 1.414213562… es un número irracional y π =
3.14157…
Luego el conjunto de números que consiste de todos los números racionales y
todos los números irracionales se conoce como el conjunto de los números reales.
b
a
....33333.0,
100
6
,25.1,25,
4
3
2,
8
7
,
4
5


20. 20
El siguiente diagrama ilustra los diferentes conjuntos numéricos que estaremos
utilizando en este curso.
PROPIEDADES DE LOS NÚMEROS REALES
Para todo número real a, b y c:
Propiedad Conmutativa: a + b = b + a
a · b = b · a
Ejemplos: 5 + 3 = 3 + 5
2 x 4 = 4 x 2
Propiedad Asociativa: a + (b + c) = (a + b) + c
a · (b · c) = (a · b) · c
Ejemplos: 2 + (3 + 4) = (2 + 3 ) + 4
5 x (1 x 7) = (5 x 1) x 7
Elemento Identidad de la Suma: a + 0 = a
Ejemplos: 8 + 0 = 8; -4 + 0 = -4
Elemento Identidad de la Multiplicación: a · 1 = a
Ejemplos: 9 x 1 = 9; -3 x 1 = -3
Inverso Aditivo: a + (-a) = 0
CONJUNTOS NUMÉRICOS
Números Reales
Números Irracionales
√3; Π; -√2; …
Números Racionales
-1; -⅔; 0; 4; ⅝;1.25,0.333…
Números Enteros
…,-3,-2,-1,0,1,2,3,…
Números Cardinales
0,1,2,3,4,5,6,…
Números Naturales
1,2,3,4,5,6,…

21. 21
Ejemplo: 6 + (-6) = 0
Inverso Multiplicativo:
Ejemplos:
Propiedad Distributiva: a · (b + c) = a · b + a · c
Ejemplo: 5 · (3 + 4) = 5 · 3 + 5 · 4
¡ PARA RECORDAR!!!!!!!
Operación Notación simbólica Elementos
Adición .a + b = c .a y b sumandos.
.c suma
Sustracción .a – b = c .a : minuendo.
.b: sustraendo
.c: resta.
Multiplicación .a . b = c .a y b : factores
.c: producto
División .a : b = c .a: dividendo
.b: divisor
.c: cociente
Potenciación .an
= b .a: base
.n: exponente
.b: potencia
Radicación n
Va = b  bn
= a .a: radicando
.n: índice
.b: raíz
Operaciones
Propiedades
Adición Sustracción Multiplicación
Ley de cierre .a N0 b  N0
a + b = c /c  N0
........................
no cumple
.a N0 b  N0
a .b =c /c  N0
Conmutativa
a + b = b + a
……………….
no cumple
a .b = b. a
Asociativa
(a + b) + c = a + (b + c)
.........................
no cumple
(a. b). c = a.(b. c)
Uniforme .a = b c = d =>
=> a + c = b + d
.a = b c = d =>
=> a - c = b - d
.a = b c = d =>
=> a . c = b . d
Elemento neutro Es el cero, pues:
.a + 0 = 0 + a = a
...........................
no cumple
Es el uno, pues:
.a . 1 = 1. a = a
Distributiva
Operaciones
Propiedades
División Potenciación Radicación
Uniforme .a = b c = d => ............................ ............................
0,1
1
 acuando
a
a
1
3
4
4
3
;1
7
1
7  xx

22. 22
=> a . c = b . d no cumple no cumple
Distributiva (a + b) : c = a: c + b: c
a .(b +c) = a . b + a . c
(a. b)n
= an
. bn
(a : b)n
= an
: bn
n
Va.b = n
Va.n
Vb
n
Va:b = n
Va : n
Vb
Actividad de Aplicación:
1) Resuelvan y verifiquen las siguientes ecuaciones. Apliquen propiedad
distributiva cuando sea necesario.
a) 5. ( a + 3) = 45 b) 8.(2.b – 4) = 16 c) 8. (p + 4 ) + 3.p – 2.p = 5 . 8 + 1
d) 0,5 . (7 + w) + 3.w = 2. ( 4 – 0,5) e) 21 + 3.(c + 7) = 92
2) Realicen los siguientes cálculos:
a) (-2)3
– 3 . (-2)2
+ 8.(-2) + 3 = b) 2. (2 + 3)2
– ½ =
c) (3 . 2) 2
+ (5 – 2 )2
= d) 2 .(2 – ½ )2
+ (2 – ½ )0
+ (1/2)2
=
¡PARA RECORDAR!
La Potenciación tiene las siguientes propiedades:
. n 4
* a = a.a.a…..a a se multiplica n veces por si misma . Ej.: 2 = 2.2.2.2
m n m+n 2 5 2+5 7
* a . a = a Ej: 3 .3 = 3 = 3
m n m-n 6 3 6-3 3
* a : a = a Ej: 3 : 3 = 3 = 3
m 3
n n.m 2 2.3 6
* (a = a Ej: 3 = 3 = 3
0 0
* a = 1 Ej: 3 = 1
1 1
* a = a Ej: 3 = 3
3) Coloquen signo igual o distinto ( = ó = ) según corresponda:
2 3 5 . .
a) 2 . 2 …… 2 |/ 9 ………..3
2 4 3 . . . . . .
b) 3 : 3 ……… 3 |/ 9 +9 …………|/ 9 + |/ 9
9 2 4 . . . . .
c) 5 : 5 ………5 |/ 4 . 9 …………. |/ 4 . |/ 9
4

23. 23
3 12 3 . . 3 . . 3. .
d) 2 ………… 2 |/ 27 – 8 ………..|/ 27 - |/ 8
2
5 7 . . . . . .
e) 3 …………. 3 |/ 36 : 9 ………|/ 36 : |/ 9
Práctico N°1 de Matemática
1)
a) Indica a cual o cuales de los siguientes conjuntos pertenecen los números de la
izquierda de la tabla con una marca de cotejo:
Número/Conjunto
numérico Natural Cardinal Entero Racional Irracional Real
11
-7
0
¾
0.272727…
7.25
2.7985413…
1½
2)
3) Calcula qué fracción de la unidad representa:
a) La mitad de la mitad.
b) La mitad de la tercera parte.
c) La tercera parte de la mitad.
d) La mitad de la cuarta parte.
25


24. 24
4) Dos automóviles A y B hacen un mismo trayecto de 572 km. El
automóvil A lleva recorridos los 5/11 del trayecto cuando el B ha
recorrido los 6/13 del mismo. ¿Cuál de los dos va primero?
¿Cuántos kilómetros lleva recorridos cada uno?
5) En las elecciones locales celebradas en un pueblo, 3/11 de los
votos fueron para el partido A, 3/10 para el partido B, 5/14 para C
y el resto para el partido D. El total de votos ha sido de 15 400.
Calcular:
1 El número de votos obtenidos por cada partido.
2 El número de abstenciones sabiendo que el número de votantes
representa 5/8 del censo electoral.
6) En cierto terreno se cultivan 4/5 partes de trigo y el resto, 100m2
, de maiz. Cuál
es la superficie total del terreno?
7) Un tonel de vino está lleno hasta los 7/11 de su capacidad. Se necesitan todavía
1804 litros para llenarlo completamente. Cuál es la capacidad del tonel?
8) Resuelve las siguientes operaciones:
Un exponente fraccionario como 1/n significa hacer la raíz n-ésima:

25. 25
Ejemplo: ¿Cuánto es 271/3
?
Respuesta: 271/3
= 27 = 3
Un exponente fraccionario como m/n significa haz la potencia m-
ésima, después haz la raíz n-ésima
Ejemplo: ¿Cuánto es 43/2
?
Respuesta: 43/2
= 43×(1/2)
= √(43
) = √(4×4×4) = √(64) = 8
RECTA REAL
Representación geométrica de los números reales.
RELACIÓN BIUNÍVOCA: a cada número real le corresponde un único punto en la
recta real y cada punto en la recta real corresponde a un único número real.
INTERVALOS
Representan subconjuntos de los números reales. Describiremos nueve tipos de
intervalos, cuatro de ellos finitos y cinco infinitos. En la definición de intervalos finitos,
a y b son números reales, siendo a < b.

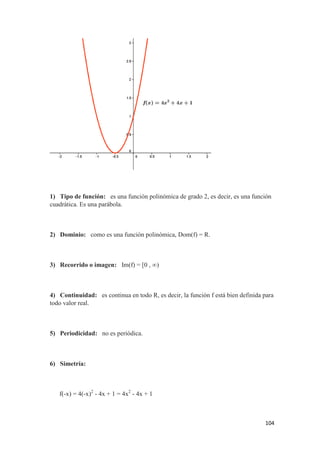
26. 26
Nota: Un extremo abierto, como puede observarse, se representa con paréntesis ( ). La
representación también puede hacerse usando circunferencias " O ". Un extremo
cerrado se representa con corchetes [ ]. La representación también puede hacerse
usando círculos ( círculo: superficie plana contenida dentro de la circunferencia,
circunferencia: línea curva cerrada, cuyos puntos están todos a la misma distancia de
un punto interior llamado centro ).
OPERACIONES CON INTERVALOS
INTERSECCIÓN: La intersección de dos intervalos A y B, se expresa por:
y se lee " A intersección B ", y representa un nuevo conjunto formado por elementos
que están en A y en B ( elementos comúnes).
_____________________________________________________________
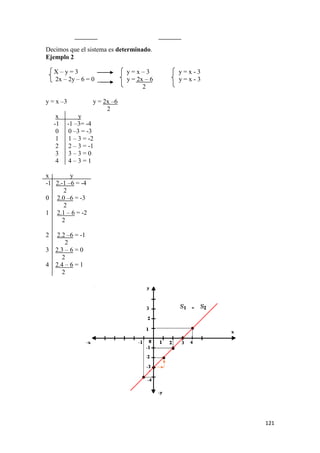
Ejemplo 1:
Sea A = ( -3, 2 ] y B = [ -1, 5 ) dos intervalos. Determinar el intervalo solución de la
intersección de A y B.
_____________________________________________________________
UNIÓN: La unión de dos intervalos A y B, se expresa por:
y se lee " A unión B ", y representa un nuevo conjunto formado por elementos que
están en A ó en B (comúnes y no comúnes).
_____________________________________________________________
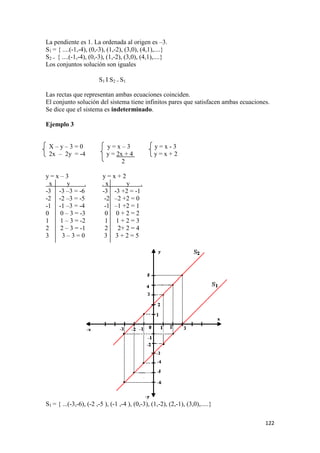
Ejemplo 2:
Sea A = ( -3, 2 ] y B = [ -1, 5 ) dos intervalos. Determinar el intervalo solución de la
unión de A y B.
De la gráfica del ejemplo Nº 1, se fija la unión de A y B como el intervalo ( - 3, 5 ).

27. 27
_____________________________________________________________
Ejemplo 3:
Sea A = ( -5, -3 ) U ( 2, 7 ) y B = ( -7, 0 ). Determinar el intervalo solución de la
intersección de A y B.
_____________________________________________________________
Ejemplo 4:
Sea A = ( -5, -3 ) U ( 2, 7 ) y B = ( -7, 0 ). Determinar el intervalo solución de la unión
de A y B.
_____________________________________________________________
DESIGUALDADES
Si a y b son números reales y a - b es positivo, se dice que a es mayor que b, y se
escribe a > b, esto es equivalente a decir que b es menor que a (b < a). Los símbolos < y
> se llaman SIGNOS DE DESIGUALDAD y expresiones como a > b y b < a se
llaman DESIGUALDADES.
PROPIEDADES DE LAS DESIGUALDADES
Si a y b son números reales, entonces:

28. 28
a) Si a > b y b > c, entonces a > c
b) Si a > b, entonces a + c > b + c
c) Si a > b, entonces a - c > b - c
d) Si a > b y c es positivo, entonces ac > bc
e) Si a > b y c es negativo, entonces ac < bc
SOLUCIÓN DE UNA DESIGUALDAD
Resolver una desigualdad con una variable significa determinar los números ( del
universo de la variable ) para los cuales la desigualdad resulta una proposición
verdadera. El conjunto de números del universo para los que es verdadera la
desigualdad, constituye la solución de la desigualdad. Por ejemplo: la solución de la
desigualdad siguiente, 3x > 9, en el universo de números reales, es la totalidad de
números reales mayores que 3, es decir:
EXPRESIONES ALGEBRAICAS
Introducción
En Álgebra se usan letras como x, y, a , b y c para representar números. Si la letra se usa
para representar cualquier número de un conjunto de números dado, se llama variable.
Una constante es ya sea un número fijo, como 5 o , o una letra que representa un
número fijo (quizá no específicado).
Las constantes y variables se combinan usando las operaciones de suma, resta,
multiplicación y división para formar expresiones algebraicas. Los siguientes son
ejemplos de expresiones algebraicas.
Para evaluar una expresión algebraica, se sustituye el valor numérico de cada variable.
Evaluación de una expresión algebraica

29. 29
Evalúe cada expresión si x=3 y y=-1.
a) x + 3y b) 5xy c) d) |-4x +y|
Solución:
Se sustituye x por 3 y y por -1 en cada expresión.
Rta: a) 0 b) -15 c) ¾ d) 13
Dominio de una variable
El dominio de la variable x en la expresión
Es {x/x≠2}, ya que si x=2, el denominador es 0, que no está definido.
Circunferencia
En la fórmula de la circunferencia C de un círculo de radio r,
El dominio de la variable r, representa el radio del círculo, es el conjunto de números
reales positivos. El dominio de la variable C que representa la circunferencia del
círculo, también es el conjunto de números reales positivos.
Al describir el dominio de una variable, se utiliza ya sea la notación de conjuntos o
palabras, lo que sea más conveniente.
Exponentes
Los exponentes enteros proporcionan un sistema de escritura rápida para representar la
multiplicación repretida de un número real.
Por ejemplo,
=
Si a es un número real y n es un entero positivo, entonces el símbolo representa el
producto de n factores de . Es decir,
= factores n. a es la base y n es el exponente. Y es la potencia.

30. 30
Aquí se entiende que =
Si , se define
= 1 si
Si y si n es un entero positivo, entonces se define
= si
Siempre que encuentre un exponente negativo, piense en “recíproco”.
Evaluación de expresiones con exponentes negativos
a) = = 8 b) = c) = = 25
Propiedades de potencias
= =
=
Raíz de un producto
La raíz de un producto es igual al producto de las raíces de los
factores:
Ejemplo
 = =
Se llega a igual resultado de la siguiente manera:
Raíz de un cociente
La raíz de una fracción es igual al cociente de la raíz del numerador entre la
raíz del denominador:
Ejemplo

31. 31

Raíz de una raíz
Para calcular la raíz de una raíz se multiplican los índices de las raíces y se
conserva el radicando:
Ejemplo
 =
Actividades:
1) Decida si cada una de las siguientes afirmaciones son verdaderas o falsas.
a) 24
. 23
= 27
b) 24
. 20
= 24
c) 24
. 21
= 24
d) 20
= 1
e) 80
= 1
f) 25
. 2-5
= 20
= 1
g) 2-5
= ½-5
h) Si a≠0 entonces a-n
= 1/an
i) Si a≠0 y si n y m son enteros entonces: (an
)m
= anxm
i) Si a>0 entonces ((an
)1/q
)q
= an
j) (q
√ an
) q
=an
k) q
√ an
) =(an
) 1/q
= an/q

32. 32
2) Se tienen los siguientes rectángulos con sus dimensiones indicadas en la figura. En
cada caso, indicar cuáles de las opciones señaladas para cada uno corresponden al
cálculo de su área
i)
ii)
iii) 3.4 + 2
iv)
v)
vi)
3)Decidir, en cada uno de los siguientes casos, si las expresiones son equivalentes.
Justificar la decisión tomada, donde ,
a) b)
4) Completar, en cada caso, las líneas punteadas de manera que las expresiones resulten
equivalente:
a) ………. b) …………
c) 2
- 6 +………………….. d) 9x -12 x2
=………….. . (3-4x)
e)
f) 3
(…….+……..)
g) 4t2
-8t5
+6t4
=………(……….-4t3
+ …….)
h) 5. (x +1)2
+ x. (x +1)2
= (x+1)2
. (……..+………..)
i)
5) Decidir cuáles de las siguientes expresiones son equivalentes a
Justificar.
a) b) c)
6) Responder a las siguientes preguntas:
a) ¿Existen valores de a y b tales que (a+b)2
= a2
+ b2
?

33. 33
b) ¿Existen valores de a y b tales que (a+b)2
< a2
+ b2
?
c) ¿Existen valores de a y b tales que (a+b)2
> a2
+ b2
?
Productos notables
Las siguientes expresiones resultan de aplicar la definición de potenciación y las
propiedades de la suma y el producto. Reciben el nombre de productos notables.
Expresiones Algebraicas
¿Que es?.
Es una colección de variables y números reales.
Sobre ellas se pueden aplicar sumas, divisiones, multiplicaciones, divisiones, potencias
y extracción de raíces.
Algunos Ejemplos de expresiones Algebraicas son:
o
Si es una variable, entonces un monomio en es una expresión de la forma ,
en donde es un numero real y es un entero no negativo. Un binomio es la suma de
dos monomios y un trinomio la suma de tres monomios
monomio binomio trinomio
Recuerda siempre que un monomio tiene solo un término, un binomio dos términos y un
trinomio tres términos.
Polinomios: Un polinomio en es la suma de cualquier numero de monomios.
Definición: Un polinomio en es una suma de la forma:
3
2
1
xy
x
y
 
  
 

3 6
5x x
x
 
x x n
ax
a n
5x 5 2x  2
1x x 
x
x

34. 34
Donde es un entero no negativo y cada coeficiente de es un numero real. Si es
diferente de cero, se dice que el polinomio es de grado
El coeficiente de la potencia más alta de es el coeficiente principal del polinomio.
Ejemplos de polinomios:
Ejemplo Coeficiente principal Grado
3 4
1 8
-5 2
8 8 0
7 1
Ejemplos de expresiones que no son polinomios:
a) b) c)
En el primer ejemplo el exponente de es negativo contradiciendo la definición de
polinomio, de igual forma con el ejemplo c donde el exponente de no es entero.
En el ejemplo b tenemos una expresión racional o fraccionaria con un polinomio en el
numerador y otro en el denominador. El criterio que utilizaremos es el siguiente si el
polinomio del denominador no es el constante o de grado cero, la expresión no es un
polinomio. Recuerde que los exponentes deben ser enteros positivos.
Operaciones con Polinomios:
1
1 1 0
...n n
n n
a x a x a x a

   
n k
a
a x
4 3
3 5 ( 7) 4x x x   
8 2
9 ( 2)x x x  
2
5 1x 
7 2x 
1
3x
x
 2
5
2
x
x


2
3 2x x 
x
x

35. 35
Suma: Sumamos términos semejantes es decir sumamos aquellos términos cuyas
variables y exponentes sean iguales. Los pasos para hacer las suma son:
Paso 1: Elimine los paréntesis
Paso 2. Agrupe términos semejantes
Paso 3. Sume y reste los términos semejantes.
Ejemplo: Halla la suma de:
=
=
=
=
Resta: Funciona igual que la suma solo hay que tener en cuenta que el signo negativo
antes de los paréntesis cambia el signo de los términos dentro del paréntesis.
Ejemplo: Resta los siguientes polinomios:
Paso 1: Si un paréntesis tiene antepuesto o detrás un signo negativo, afecte los signos
dentro del paréntesis cambiándolos por el opuesto y reemplaza el signo negativo que se
encuentra antes del paréntesis por uno positivo.
3 2 3 2
( 2 5 7) (4 5 3)x x x x x     
3 2 3 2
( 2 5 7) (4 5 3)x x x x x     
3 2 3 2
2 5 7 4 5 3x x x x x     
3 23 2
(2( 54 ) ) 7 )5 ( 3x xx x x   
23
( ( 3 ) 5 0) 15 ( )x xx  
3 2
5 3 5 10x x x  
3 2 3 2
( 2 5 7) (4 5 3)x x x x x     
3 2 3 2
(4 5 3) ( 4 5 3)x x x x       

36. 36
Paso 2: Elimine los paréntesis. Para hacerlo solo escriba los términos que están dentro
de los paréntesis con sus signos correspondientes e ignore el signo + que entre los dos
paréntesis.
Paso 3: Agrupe los términos semejantes es decir los términos con iguales variables e
iguales exponentes.
Paso 4: Sume y reste los términos semejantes.
Así que aplicando este concepto a la expresión entera tendríamos:
Multiplicación:
Ejemplo 1. Multiplicación de monomio por monomio:
Multiplicamos las constantes o números y las variables
=
=
Ejemplo 2. Multiplicación de monomio por polinomio:
32
(2 3 1)5 xx x   22 3 2
( 5 ) ( 5 )(2 ) (3 ) ( 1( 5 ) )x xx x x    
5 3 2
10 15 5x x x  
=
=
=
=
3 2 3 2
( 2 5 7) (4 5 3)x x x x x     
3 2 3 2
( 2 5 7) ( 4 5 3)x x x x x    
3 2 3 2
2 5 7 4 5 3x x x x x     
3 3 2 2
4 5 2 5 7 3x x x x x    
3 2
3 7 5 4x x x   

37. 37
=
=
=
=
=
a. Método vertical
División:
Ejemplo1: División de polinomio entre un monomio
Expresa como un polinomio en y :
Paso1: Dividimos cada termino del numerador entre
2
(2 1)( 3 1) x xx   2 2
(2 1) (21 )3 1x x x xx    
2 2
(2 ) ( ) (( 3 ) ( 3 ) ( 3 ) (1) (2 ) (1) ) (1( (1) )1)x x xx x x x    
3 2 2
6 3 3 2 1x x x x x     
3 2 2
6 3 2 3 1x x x x x     
3 2
6 2 1x x x   
2
2 1x x 
3 1x 
3 2
6 3 3x x x  
2
2 1x x 
3 2
6 2 1x x x   
x y
2 3 3 2
6 4 10
2
x y x y xy
xy
 
2xy

38. 38
=
Paso2: Simplificamos.
=
Expresión algebraica no entera o fraccionaria o racional es la expresión que es cociente
de polinomios Q(x) P(x), siempre que el polinomio denominador no sea un polinomio
constante (ni nulo) o aquéllas en que las variables son bases de potencias de exponente
negativo.
Ejemplos de expresiones racionales son:
Ya que el denominador no puede ser cero las variables de los polinomios
denominadores no pueden tomar los valores que son raíces. Como una expresión
racional es un cociente entre números reales, las propiedades de fracciones también se
cumplen en los casos de las expresiones racionales.
Decimos que una expresión racional está en su forma mínima si el numerador y el
denominador no tienen factor común diferente de 1 y –1. Si una expresión racional
determinada no está en su forma mínima puede sustituirse por un equivalente
factorizando el numerador y el denominador, y luego dividiendo ambos entre los
factores comunes.
Esto podemos justificarlo mediante la propiedad de las fracciones que establece que
Multiplicación de expresiones algebraicas
2 3 3 2
6 4 10
2
x y x y xy
xy
 
2 3 3 2
6 4 10
2 2 2
x y x y xy
xy xy xy
 
2 3 3 2
6 4 10
2
x y x y xy
xy
  2 2
3 2 5xy x y 

39. 39
Para multiplicar expresiones racionales usamos la siguiente propiedad de fracciones:
si R(x) = S(x) entonces podemos simplificar y nos queda
Ejemplos:
Cocientes de expresiones fraccionarias
La propiedad de fracciones que se usa para dividir expresiones fraccionarias es la
siguiente
Ejemplos:
Suma y diferencia de expresiones fraccionarias

40. 40
La suma y diferencia de expresiones fraccionarias se resuelven aplicando las
propiedades de fracciones ya mencionadas cuando nos referimos al conjunto de
números fraccionarios Z.
Ejemplo:
Resolver la siguiente expresión algebraica :
Lo primero que debemos hacer es encontrar el mínimo común múltiplo (mcm es el
mismo concepto que en números reales)
luego cada
una de las expresiones fraccionarias dadas es reemplazada por una equivalente que
contenga al MCD como su denominador y después de aplicar las propiedades
correspondientes realizamos las operaciones:
Si una fracción tiene otra fracción en e numerador o denominador, o en ambos se
llama fracción compuesta, y si no, se denomina fracción simple. Los métodos que se
usan para simplificar expresiones fraccionarias compuestas son los mismos que se usan

41. 41
en números fraccionarios. La multiplicación del numerador y denominador por el MCD
es el método más sencillo.
Ejemplo: Llevar a la mínima expresión la siguiente fracción algebraica compuesta
¿qué te parece si primero trabajamos con el numerador , es decir con
?
El MCD entre (x-1) y (x-2) es... ¡¡ (x-1)(x-2) !!, y realizando la resta tenemos:
Ahora tenemos que trabajar con el denominador, es decir con
Y por último vamos a unir correctamente los resultados obtenidos y a operar....
es decir que la respuesta es ...

42. 42
Actividades
1.- Obtener el producto entre las siguientes expresiones y simplificar hasta su forma
mínima.
2.- Obtener el cociente en su forma mínima:
3.- Determinar la suma o diferencia de las siguientes expresiones en su forma mínima:

43. 43
4.- Lleva a la mínima expresión las siguientes fracciones algebraicas compuestas:
RESUMEN
Sean A y B expresiones algebraicas entonces....
El MCD(A,B) es la expresiones algebraicas que se obtiene del producto de todos los
divisores comunes de A y B irreducibles y de menor exponente.
Operaciones con Fracciones Algebraicas:
Ejercicio 1
Dadas las siguientes expresiones algebraicas :
Ejercicio 2

44. 44
Ejercicio 3
Ejercicio 4 Operar y simplificar las siguientes expresiones algebraicas:
Expresiones Algebraicas Racionales
Llamaremos expresiones algebraicas racionales a las de la forma
)x(B
)x(A donde A(x) y
B(x) son polinomios de variable x , y B(x)  0.
Por ejemplo,
2
7
x
es una expresión algebraica racional porque el numerador A(x) = 7 es
un polinomio y el denominador B(x) = x  2 también es un polinomio.
También es una expresión algebraica racional
xx
xx
7
32
2
3

 .
¿Es
3
3 35


x
xx una expresión algebraica
racional?..............................................................................

45. 45
La expresión x 2
 9 es también racional porque x 2
 9 es un polinomio y 1, su
denominador, también lo es.
Simplificación de expresiones racionales
Recordamos que, dado el racional
3
2 podemos hallar otros equivalentes con él:
...
21
14
6
4
3
2
 donde 0ncon
nb
na
b
a



 .
Análogamente para la expresión racional
)x(B
)x(A pueden hallarse expresiones racionales
equivalentes:
)x(N)x(B
)x(N)x(A
)x(B
)x(A


 siendo N(x) cualquier polinomio no nulo.
En Z muchas veces se nos presenta el problema de encontrar la fracción equivalente
más simple que una dada. Por ejemplo,
12
7
1132
117
132
77
2




También es posible simplificar expresiones algebraicas racionales cuando existen
factores comunes al numerador y al denominador, de lo contrario la expresión racional
es irreducible.
Consideremos
3xx3x
1x
23
2

 . Factorizamos su numerador y su denominador:
)1x()1x(1x2

)1x()1x()3x()1x()3x()3x()3x(x3xx3x 2223

Entonces
3x
1
)1x()1x()3x(
)1x()1x(
3xx3x
1x
23
2






 si x  1 y x  1
Las dos expresiones racionales,
3xx3x
1x
23
2

 y
3x
1

son equivalentes para x  1 y x
 1.
La expresión final es equivalente a la dada para todo valor de x que no anule el factor
cancelado porque ello equivaldría a dividir por cero.
Veamos otros ejemplos:
I) 2xsi
2x
)2x(x3
)2x()2x(
)2x()2x(x3
)2x(
)4x(x3
4x4x
x12x3
2
2
2
3












II) Rx
5x
1
)5x()5x(
5x
25x
5x
222
2
4
2








¿Por qué esta igualdad es válida para
cualquier número real? .......................................................................................................
Actividad:
Simplificar, indicando para qué valores de x la expresión resultante es equivalente a la
dada.
a)
9x6x
6x2
2

 b)
1x
xx2

 c)
x49x14x
x49x
23
3

 d)
2x3x
6xx
2
2



46. 46
Operaciones con Expresiones Algebraicas Racionales
Para operar con expresiones racionales, aplicamos las mismas propiedades y técnicas
que para operar con fracciones numéricas.
Adición y Sustracción
Recordamos que para sumar
21
1
14
3
 necesitamos hallar fracciones equivalentes a los
sumandos, de igual denominador:
42
11
732
2133
73
1
72
3
21
1
14
3







 .
Para sumar (o restar) expresiones racionales de distinto denominador, debemos sumar
(o restar) expresiones equivalentes a ellas que tengan el mismo denominador. Para
hallarlo, factorizamos los denominadores y luego multiplicamos los factores comunes y
no comunes con el mayor exponente con el que figura (mínimo común múltiplo).
Veamos el siguiente ejemplo: 


 4x3x
x
3x6x3
2
22
Factorizamos los denominadores:









)4x()1x(
x
)1x(3
2
)4x()1x(
x
)1x2x(3
2
22
Buscamos expresiones equivalentes
con igual denominador: 






)4x()1x(3
)1x(3x
)4x()1x(3
)4x(2
22
Operamos en el numerador y sumamos:
)4x()1x(3
8xx3
)4x()1x(3
x3x38x2
2
2
2
2






El numerador no tiene raíces reales, por lo tanto la expresión obtenida es irreducible.
Vamos a calcular 





4x
4x2
10x3x
10x
22
Factorizamos los denominadores: 






)2x()2x(
4x2
)5x()2x(
10x
Elegimos un denominador común y hallamos las expresiones equivalentes:







)2x()5x()2x(
)5x()4x2(
)2x()5x()2x(
)2x()10x(
Aplicamos propiedades y restamos: 






)2x()5x()2x(
20x4x10x2
)2x()5x()2x(
20x10x2x 22
)5x()2x(
)20x(
)2x()5x()2x(
)2x()20x(
)2x()5x()2x(
40x22x
)2x()5x()2x(
20x14x220x8x 222












La suma de expresiones algebraicas racionales es asociativa, conmutativa, cumple la ley
de cierre y posee elemento neutro: 0. Recordemos que restar es sumar el opuesto.
Actividad:
Calcular:

47. 47
a) 





 x3
1
9x6x
1x
9x
2
22
b) 







2x2
21
20x6x2
2x
25x
5x
22
c) 




 222
)1x(
1
1x
2
)1x(
1
Multiplicación
Para multiplicar dos expresiones racionales
)x(D
)x(C
y
)x(B
)x(A , procedemos así:
)x(D)x(B
)x(C)x(A
)x(D
)x(C
)x(B
)x(A



Por ejemplo:
I)
3x2x
x3x6
)1x()3x(
x3)1x2(
1x
x3
3x
1x2
2
2










II) Calculamos ahora 








)x4x()9x(
)15x5()x4x(
x4x
15x5
9x
x4x
232
2
232
2
Factorizamos cada uno de los polinomios: 



)4x(x)3x()3x(
)3x(5)4x(x
2
Simplificamos y obtenemos el resultado: 3xy4xsi
)3x(x
5



 .
La multiplicación de expresiones algebraicas racionales cumple con la ley de cierre, es
asociativa, conmutativa, tiene elemento neutro (1) y es distributiva respecto de la suma
y la resta.
¿Existe inverso multiplicativo para toda expresión
)x(B
)x(A ?
...........................................................................................................................
Actividad:
Resolver: a)
8x12x6x
12x6
x2
4x4x
23
2




b)
1x2x
1
1xx
1x
)1x(
22
3





División
Se llama inverso multiplicativo de una expresión algebraica racional
)x(B
)x(A a la expresión
)x(A
)x(B , si A es no nulo.
Para dividir dos expresiones algebraicas racionales
)x(B
)x(A y
)x(D
)x(C operamos igual que en el
conjunto Q:
)x(C)x(B
)x(D)x(A
)x(C
)x(D
)x(B
)x(A
)x(D
)x(C
:
)x(B
)x(A


 con C(x)  0
Por ejemplo:
2
2
x2x6
2xx
x2)x3(
)2x()1x(
2x
x2
:
x3
1x









48. 48
Actividad:
1) Con las expresiones
6xx
3x
)x(Ty
9x
4x2
)x(P
22





 calcular:
a) P(x) . T(x) b) P(x) : T(x) c) T(x) : P(x).
2) Resolver: a)
3x
16x
:
9x
4x 4
2
2



 b)
1x
6x3
:
1x
10x5
2 



c)
1x
4x3x
:
1x
1x
1x
4x
4
2
22













Actividad:
Efectuar los siguientes ejercicios combinados:
a)
10x4
9x
6xx
2x
4x
2x 2
22 











 b)
4x
4
:
2x
1
2x
1
2










c)
4x
4
:
2x
1
2x
1
2



d) 





 1
x
1
:)xx( 3
TRABAJO PRÁCTICO DE EXPRESIONES ALGEBRAICAS RACIONALES
Realizar las siguientes operaciones, simplificando los resultados cuando sea posible:
a)
1x
1x
1x
x
4
4
2
2





b)
2
2
23
)1x(x
1x2x
xx
1x
3
1






c)
1x
2x
:
xx
6xx
43
2




d)
5
7x
:
7x
x
7x
3x
9x
6x2
2







e)
9x
1
)3x(
2
3x
1
22





f)
3
22
22
2
x9
1x2x
:
x3
)1x2(
1x4
1x2
x3
1x2 







 




g) 














1x
x
x:
1x
x
x

49. 49
Razones y proporciones
Matemáticamente, hablamos de proporcionalidad cuando dos
magnitudes están relacionadas de modo que si una varía produce una
variación en la otra.
Al comparar dos magnitudes podemos darnos cuenta de distintas
relaciones:
‐ El aumento de una de ellas al doble, el triple, etc., produce que la otra
aumente en la misma proporción, es decir, el doble, el triple. Entonces,
estas magnitudes guardan una proporcionalidad directa.
‐ El aumento de una de ellas al doble, el triple, etc., produce que la otra
se reduzca a la mitad, la tercera parte… Entonces, estas magnitudes
guardan una proporcionalidad inversa.
‐ Si no se cumple ninguna de las anteriores no hay proporcionalidad.
El estudio de la proporcionalidad es una de las ramas más antiguas de la
Matemática y ha supuesto una importante contribución en el desarrollo de
ésta. Ya el matemático griego Euclides (alrededor del 325 a. C.- Alejandría,
alrededor del 265 a. C.) en el libro quinto de su obra “Los Elementos” trata
de la teoría de la proporción. No obstante, la primera aplicación de las
proporciones se atribuye a Thales de Mileto (Mileto, hacia 624 a.C.- hacia
547 a.C.).
Hablar de proporcionalidad conlleva hablar del concepto de razón
entre dos números.
Definición La razón entre dos cantidades es el cociente o división entre ambas.
Se escribe siempre en forma de fracción e indica el número de veces que es mayor
una cantidad que la otra.
Razón entre a y b: a/b
Una proporción numérica es la igualdad entre dos razones:
Se lee “a es a b como c es a d”. Llamamos extremos a a y b, y medios a c y d.
El valor de este cociente (una vez efectuada la división) recibe el nombre de constante
de proporcionalidad.

50. 50
En toda proporción se cumple la propiedad fundamental de las proporciones:
Propiedad: En toda proporción el producto de los extremos es igual al producto de los
medios.
Ejemplo
En una lata de pintura de pared se indica que con sus de 4 litros da para pintar una
superficie de 16 metros cuadrados, aproximadamente.
La siguiente tabla muestra la cantidad de pintura necesaria para pintar
paredes según el área que ocupen:
Superficie de pared a pintar (m2
) 16 32 8 4 12 20
Litros de pintura necesarios 4 8 2 1 3 5
Proporcionalidad inversa
Dos magnitudes son inversamente proporcionales si al variar una la otra varía de la
forma inversa. Es decir, si, por ejemplo, una aumenta el doble o el triple la otra
disminuye la mitad o la tercera parte, respectivamente; o si una se reduce a la mitad,
la otra aumenta el doble.
Magnitudes inversamente proporcionales son: la velocidad de un móvil y el tiempo que
tarda en recorrer una determinada distancia, el número de participantes en un sorteo y
la probabilidad de obtener premio, el tiempo que se tarda en imprimir 1000 páginas y
el número de impresoras que se empleen para ello.
Ejemplos de proporcionalidad inversa:
1. Un grupo de 4 empleados limpia un edificio de oficinas en 8 horas. ¿Cuánto
tardarían en hacer el mismo trabajo 5 empleados?, ¿y 8 empleados? El número de
empleados y el tiempo son magnitudes inversamente proporcionales puesto que:
cuantos menos empleados limpien, más tardarán; cuantos más empleados limpien,
menos tardarán
Al ser un caso de proporcionalidad inversa averiguamos primero el número de horas
que necesita un empleado para limpiar todo el edificio, y después lo dividimos entre el
número de empleados correspondiente.
Si 4 empleados tardan 8 h. uno solo tardará cuatro veces más, o sea, 32 h. ( 8 . 4 =
32)

51. 51
Si un empleado tarda 32 h. 5 tardarán 5 veces menos, o sea, 6’4 h. = 6 h. y
24 minutos. (32: 5 = 6, 4 ).
Actividades:
Leer atentamente cada uno de los siguientes enunciados, identificar la situación
problemática, extraer datos e incógnitas y resolver:
1) Con 12 botes conteniendo cada uno ½ kg de pintura se han pintado 90 m de
verja de 80 cm de altura. Calcular cuántos botes de 2 kg de pintura serán
necesarios para pintar una verja similar de 120 cm de altura y 200 metros de
longitud.
2) 11 obreros labran un campo rectangular de 220 m de largo y 48 de ancho en 6
días. ¿Cuántos obreros serán necesarios para labrar otro campo análogo de
300 m de largo por 56 m de ancho en cinco días?
3) Seis grifos, tardan 10 horas en llenar un depósito de 400 m³ de capacidad.
¿Cuántas horas tardarán cuatro grifos en llenar 2 depósitos de 500 m³ cada
uno?
4) De los 800 alumnos de un colegio, han ido de viaje 600. ¿Qué porcentaje de
alumnos ha ido de viaje?
5) Al adquirir un vehículo cuyo precio es de 8800 €, nos hacen un descuento del
7.5%. ¿Cuánto hay que pagar por el vehículo?
6) Resolver cada una de las siguientes ecuaciones. Utiliza la propiedad
fundamental de las proporciones.
Si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos
determinados en una de las rectas son proporcionales a los segmentos
correspondientes en la otra.

52. 52
Ejemplos
1 Las rectas a, b y c son paralelas. Halla la longitud de x.
2 Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas
a y b?

53. 53
Sí, porque se cumple el teorema de Thales.
Teorema de Thales en un triángulo
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de
los lados del triangulo, se obtiene otrotriángulo AB'C',
cuyos lados son proporcionales a los del triángulo ABC.
Ejemplo:
Hallar las medidas de los segmentos a y b.

54. 54
Aplicaciones del teorema de Thales
El teorema de Thales se utiliza para dividir un segmento en varias partes iguales.
Ejemplo:
Dividir el segmento AB en 3 partes iguales.
1 Se dibuja una semirrecta de origen el extremo A del segmento.
2 Tomando como unidad cualquier medida, se señalan en la semirrecta 3
unidades de medida a partir de A

55. 55
3 Por cada una de las divisiones de la semirrecta se trazan rectas paralelas al
segmento que une B con la última división sobre la semirrecta. Los puntos
obtenidos en el segmento AB determinan las 3 partes iguales en que se divide.
Trigonometría
Razones trigonométricas
En los triángulos semejantes los ángulos son iguales y los lados homólogos son
proporcionales. La razón entre los lados de un triángulo determina su forma.
Dado un triángulo rectángulo, las razones trigonométricas del ángulo agudo α se
definen:
 � El seno es el cociente entre el cateto opuesto y la hipotenusa.
 El coseno es el cociente entre el cateto adyacente y la hipotenusa.
 La tangente es el cociente entre el cateto opuesto y el cateto adyacente.
Estas razones no dependen del tamaño del triángulo sino del ángulo.
Un ingeniero observa la torre de Burj Khalifa en Dubai, bajo un ángulo de elevación de
70° 8’. Si él se encuentra a 300 m del punto medio de la base de la torre. ¿Cuál es la
altura aproximada de la torre? Puede comprobar tu resultado buscando más
información sobre ella.

56. 56
2)El mástil de la costanera "Vuelta Fermosa" tiene 35 m de altura. Una persona
sentada en un banco observa el extremo superior del mástil bajo un ángulo de
elevación de 38° 9'. ¿A qué distancia de la base del mástil se encuentra?
3) La altura de la Torre Litoral de Formosa es de 34 m aproximadamente. A qué
distancia deberá colocarse un observador para ver el borde de la terraza bajo un
ángulo de elevación de 41°35’?
4) Un observador se coloca a 38, 64 m de la base de la Torre y mira el borde de la
terraza bajo un ángulo de elevación de 41°35’. ¿Cuál será la altura de la torre?
5) En un triángulo rectángulo la hipotenusa mide 6,73 cm y uno de sus ángulos mide 48°1’.
¿Cuántos miden los catetos? No vale medir.

57. 57
la figura se ha representado el ángulo α en la circunferencia goniométrica o de radio
unidad.
En el triángulo rectángulo que se forma como la hipotenusa es 1, el cateto opuesto es el
sen α y el adyacente el cos α.
Es importante recordar el siguiente triángulo:
Observa que (cos α, sen α) son las coordenadas del punto final del ángulo α en la
circunferencia de radio unidad.

58. 58
Actividades
En el triángulo de la figura calcula:
a) sen α d) sen β
b) cos α e) cos β
c) tg α f) tg β
Obtén con la calculadora:
a) sen 30º = 0,5
b) cos 60º = 0,5
c) tg 45º = 1
Relaciones fundamentales
Si se aplican la semejanza y el teorema de Pitágoras a los triángulos rectángulos
"básicos", es decir, con hipotenusa=1 o con cateto adyacente=1, se obtienen las
relaciones fundamentales de la trigonometría:
Los triángulos OBA y OB’A’ son semejantes:

59. 59
Aplicando el Teorema de Pitágoras al triángulo OBA de la figura obtenemos:
Resolución de triángulos rectángulos
Resolver un triángulo rectángulo es calcular los datos desconocidos, lados o ángulos, a
partir de los conocidos.
Veamos los casos que se pueden presentar.
a) Conocidos un ángulo y la hipotenusa

60. 60
Para hallar los catetos de un triángulo rectángulo del que se conocen las medidas de la
hipotenusa y de un ángulo agudo, pensaremos en el triángulo:
Razones de cualquier ángulo
Recuerda que (cos α, sen α) eran las coordenadas del punto final del ángulo α en la
circunferencia de radio unidad. Esto que vimos para los ángulos agudos podemos
hacerlo extensible a ángulos cualesquiera.
El seno
El seno de un ángulo es la coordenada vertical del punto final del recorrido del ángulo
sobre la circunferencia goniométrica.
Observa que su valor está comprendido entre -1 y 1.

61. 61
El coseno
De la misma manera que el seno de un ángulo es la ordenada, el coseno es la abscisa
del punto final del recorrido que marca el ángulo en la circunferencia.
Su valor también está comprendido entre -1 y 1.
La tangente
Con la relación fundamental tg α=senα/cosα se amplia la definición de tangente en
ángulos agudos a un ángulo cualquiera.
La tangente se representa en la recta tangente a la circunferencia goniométrica en el
punto (1,0).
Para los ángulos de 90º y 270º, el coseno es 0 por lo que no está definida la tangente;
cuanto más se acerca un ángulo a 90º o a 270º, mas grande se hace en valor absoluto la
tangente, diremos que es infinito
Resolver problemas métricos

62. 62
La trigonometría es útil para resolver problemas geométricos y calcular longitudes en la
realidad.
Con un teodolito como el de la fotografía, se pueden medir ángulos, tanto en el plano
vertical como en el horizontal, que nos permiten, aplicando las razones trigonométricas,
hallar distancias o calcular alturas de puntos inaccesibles.
En estos casos aunque el triángulo de partida no sea rectángulo, trazando su altura
podemos obtener dos triángulos rectángulos a resolver con los datos que tenemos.
Veamos algunos ejemplos.
Calcular medidas topográficas
Para medir la anchura de un río se han medido los ángulos de la figura desde dos puntos
de una orilla distantes 160 m. ¿Qué anchura tiene el río?.

63. 63
Actividades:

64. 64
1. Expresa en radianes:
a) 15° b) 120° c) 240° d) 345°
2. Expresa en grados:
a) /15 b)3 /10 c)7 /12 d)11 /6
3. Halla con la calculadora las siguientes razones redondeando a centésimas:
a) Sen 25° b) cos 67° c) tg 225° d) tg 150°
4. Un ángulo de un triángulo rectángulo mide 47° y el cateto opuesto 8 cm, halla la
hipotenusa.
5. La hipotenusa de un triángulo rectángulo mide 26 cm y un ángulo 66°. Calcula
los catetos.
6. Un ángulo de un triángulo rectángulo mide 44° y el cateto adyacente 16 cm,
calcula el otro cateto.
Teorema del seno
En este tema has podido resolver triángulos que no eran rectángulos considerando la
altura.

65. 65
El resultado conocido como Teorema del seno, nos permite resolver triángulos
cualesquiera si conocemos un lado y dos ángulos.
Teorema del Coseno
El teorema del Seno no se utiliza directamente para resolver triángulos si conocemos
dos lados y el ángulo formado entre ellos, o si conocemos los tres lados. Para estos
casos utilizaremos el teorema del coseno.
Del triángulo ABC
Ejercicios propuestos:
1. En los siguientes ejercicios: a, b, y c son las medidas de los lados de un triángulo,
mientras que α, β, γ son las medidas de los ángulos opuestos a esos lados,
respectivamente.
Resuelve el triángulo en cada caso:
a) a = 10 cm. b= 12 cm. γ = 35º
b) a = 7 m. b = 6 m. c = 4 m.

66. 66
c) c = 10 cm. β = 40º α = 70º
d) a = 12 cm. b = 16 cm β = 43º
e) α = 53º β = 75º c = 30,5 cm.
f) α = 48º γ = 68º c = 47,2 mm.
2. Dos lados adyacentes de un paralelogramo se cortan en un ángulo de 36º y tienen
longitudes de 3 y 8 cm. Determina la longitud de la diagonal menor.
3. Dos trenes parten simultáneamente de una estación en dirección tal que forman un
ángulo de 35º. Uno va a 15 km/hr y el otro a 25 km/hr. Determina a qué distancia se
encuentran separados después de dos horas de viaje.
4. Determina las longitudes de las diagonales de un paralelogramo, conocidos los lados
m y n, y el ángulo a entre ellos.
Ejercicios con soluciones para aplicar los teoremas vistos anteriormente.
1.- De un triángulo se conocen los ángulos B = 120º y C = 30º y el lado a = 3 m.,
resuelve el triángulo.
Indicación: Empieza calculando A = 30º y después aplica el teorema del seno dos veces
y obtendrás:
2.- Resuelve un triángulo del que se conocen a = 4,7 m., b = 2,2m. y C = 54º.
Indicación: Aplicando el teorema del coseno obtienes que c = 14,77m. Aplicando ahora
el teorema del coseno para cos A se obtiene que A = 98º26’24” y
como A + B + C = 180º tenemos que B = 27º33’36”.
3.- Resuelve el triángulo del que se conocen: A = 40º, b = 5m, a = 2m.
Indicación: Aplicamos teorema del seno:
que este triángulo no tiene solución, ya que el seno no puede ser mayor que 1.
4.- Resuelve el triángulo del que se conocen: A = 40º, b = 5m, a = 4m.
Indicación: Empieza como en el anterior, pero este sí tiene solución:

67. 67
5.- Resuelve el triángulo del que se conocen a = 7m, b = 9m y c = 3m.
Indicación: Aplica tres veces el teorema del coseno y obtienes: A = 40º36’, B =
123º12’, C = 16º12’
6.- Una persona observa un globo desde dos posiciones distintas situadas en un mismo
plano vertical que pasa por el globo. Dichas posiciones distan entre sí 0,9 km. Las
visuales, del observador al globo, forman 20º y 30º con la horizontal. Halla la altura del
globo. Solución: 201m.
7.- Dos lados de un paralelogramo miden 2 y 3m y forman un ángulo de 50º. Halla las
longitudes de las diagonales del paralelogramo.
Indicación: Dibuja un paralelogramo de lados 2 y 3 m y el ángulo entre ellos de 50º. El
ángulo opuesto debe medir 130º. Aplica a las dos diagonales el teorema del coseno y
obtendrás: 2,30m y 4,55m.
Vectores
Sistema de referencia y coordenadas cartesianas
Grafica de ejes cartesianos ortogonales.
Proyeccion ortogonal en los ejes x e y
Definir magnitud escalar y vector
Cómo se grafica un vector
Magnitudes Escalares
Denominamos Magnitudes Escalares a aquellas en las que las medidas quedan
correctamente expresadas por medio de un número y la correspondiente unidad.
Ejemplo de ello son las siguientes magnitudes, entre otras:
Masa
Temperatura

68. 68
Presión
Densidad
Magnitudes vectoriales
Las magnitudes vectoriales son magnitudes que para estar determinadas precisan de un
valor numérico, una dirección, un sentido y un punto de aplicación.
Vector
Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial.
Podemos considerarlo como un segmento orientado, en el que cabe distinguir:
 Un origen o punto de aplicación: A.
 Un extremo: B.
 Una dirección: la de la recta que lo contiene.
 Un sentido: indicado por la punta de flecha en B.
 Un módulo, indicativo de la longitud del segmento AB.
Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos
uso de dos vectores unitarios o versores. Estos vectores unitarios, son
unidimensionales, esto es, tienen módulo 1, son perpendiculares entre sí y
corresponderán a cada uno de los ejes del sistema de referencia.
Por ello, al eje de las X, le dejaremos corresponder el vector unitario o también
denominado .
Del mismo modo, al eje Y, le corresponderá el vector unitario o también denominado
.
Por tanto, obtendríamos un eje de coordenadas cartesianas de la siguiente forma:

69. 69
Vectores iguales
Dos vectores son iguales cuando tienen el mismo módulo y la misma dirección.
Vector libre
Un vector libre queda caracterizado por su módulo, dirección y sentido. El vector libre
es independiente del lugar en el que se encuentra.
Vectores unitarios y componentes de un vector
Cualquier vector puede ser considerado como resultado de la suma de tres vectores,
cada uno de ellos en la dirección de uno de los ejes coordenados.
x yr = r + r
r r r
Si consideramos ahora sobre cada eje un vector, aplicado en el origen, cuyo sentido es
positivo y cuyo módulo consideramos como unidad de longitudes, podemos sustituir
cada uno de los sumandos de la expresión anterior por el producto de un escalar por el
correspondiente vector unidad.
De ese modo,
Los escalares , y se denominan componentes del vector y se representan por:

70. 70
Los vectores son los vectores unitarios y suelen representarse
respectivamente por i, j, y k.
También puede representarse de la siguiente forma:
Suma y resta de vectores
La suma de dos vectores libres es otro vector libre que se determina de la siguiente
forma: Se sitúa el punto de aplicación de uno de ellos sobre el extremo del otro; el
vector suma es el vector que tiene su origen en el origen del primero y su extremo en el
extremo del segundo. Por tanto, el vector suma de dos vectores coincide con una de las
diagonales, la "saliente", del paralelogramo que puede formarse con los vectores que se
suman; la otra diagonal representa la resta de dichos vectores.
Para efectuar sumas o restas de tres o más vectores, el proceso es idéntico. Basta con
aplicar la propiedad asociativa.
Al vector que se obtiene al sumar o restar varios vectores se le denomina resultante.
Una vez establecido el sistema de referencia, se puede identificar cualquier punto de la
recta o del plano por medio un número (unidimensional) o dos números (bidimensional)
que son sus coordenadas. La posición también la podemos representar por un segmento

71. 71
orientado (flecha), que va desde el origen del sistema de referencias (Figura 3.3). Este
segmento orientado OA
uuur
está caracterizado por la dirección de la recta que pasa por
OA, por el sentido de esta recta de O hacia A y por longitud del segmento OA. Este
segmento dirigido se llama vector y se lo representa gráficamente mediante letras
mayúsculas o minúsculas con una flecha sobre ellas o en negrita ( a
r
, A
r
, a ó A).
La expresión del vector posición r
r
en un sistema de referencia bidimensional es:
x yr = r i + r jˆ ˆr
donde: iˆ y jˆ son los vectores unitarios correspondientes a los ejes x e y,
xr iˆ y yr jˆ son las componentes vectoriales,
xr y yr son las componentes escalares.
Suma de Vectores
La suma de los vectores podemos realizarla de dos maneras diferentes, analítica y
gráficamente.
Procedimiento Gráfico
Para sumar dos vectores de manera gráfica utilizaremos la denominada Regla del
paralelogramo, consistente en trasladar paralelamente los vectores hasta unirlos por el
origen, y luego trazar un paralelogramo, del que obtendremos el resultado de la suma,
como consecuencia de dibujar la diagonal de ese paralelogramo, como podemos ver en
el siguiente dibujo:

72. 72
Otra manera de expresar la suma de manera gráfica es trasladar el segundo vector a
sumar de tal manera que el origen de éste, coincida con el extremo del primer vector, y
la suma la obtendremos dibujando un vector que vaya desde el origen del primer vector
hasta el extremo del segundo, de la siguiente manera:
Hay que tener muy presente lo siguiente: vectores en la misma dirección se suman (tal y
como ya hemos visto en la sección de la suma de vectores), pero vectores con sentidos
opuestos se restan (tal y como se puede ver en el apartado correspondiente a la resta de
vectores). A continuación tenemos un ejemplo de suma y resta de vectores.

73. 73
Método Algebraico para la Suma de vectores
Dados tres vectores
La expresión correspondiente al vector suma es:
o bien
siendo, por tanto,
La suma de vectores goza de las siguientes propiedades:
Conmutativa
a + b = b + a
Asociativa

74. 74
(a + b) + c = a + (b + c)
Elemento neutro o vector 0
a + 0 = 0 + a = a
Elemento simétrico u opuesto a'
a + a' = a' + a = 0
a' = -a
Producto de un vector por un escalar
El resultado de multiplicar un escalar k por un vector v, expresado analíticamente por
kv, es otro vector con las siguientes características :
1.- Tiene la misma dirección que v.
2.- Su sentido coincide con el de v, si k es un número positivo, y es el opuesto, si k es
un número negativo.
3.- El módulo es k veces la longitud que representa el módulo de v. ( Si k es 0 el
resultado es el vector nulo).
Analíticamente, tenemos que multiplicar el escalar por cada una de las coordenadas del
vector.
Ejemplo : Dado el vector v de componentes : vxi + vyj + vzk, el producto 3 · v = 3 · vxi
+ 3 · vyj + 3 · vzk.
La representación gráfica del producto es igual a sumar el vector tantas veces como
indica el escalar.
Ejemplo :

75. 75
Módulo de un vector
Un vector no solo nos da una dirección y un sentido, sino también una magnitud, a esa
magnitud se le denomina módulo.
Gráficamente: es la distancia que existe entre su origen y su extremo, y se representa
por:
Coordenadas cartesianas: En muchas ocasiones es conveniente tomar las componentes
sobre tres direcciones mutuamente perpendiculares OX, OY y OZ que forman un
sistema cartesiano tridimensional.
Si tomamos tres vectores unitarios, i sobre OX, j sobre OY y k sobre OZ, entonces
podemos encontrar puntos ax, ay, az sobre OX, OY, OZ, respectivamente, tales que:

76. 76
y aplicando el teorema de Pitágoras nos encontramos con que el módulo de a es:
Álgebra vectorial
SUMA DE VECTORES
Dados dos vectores A y B como representamos, definimos la suma A + B = C de
forma tal que Cx = Ax + Bx y Cy = Ay + By. Como las coordenadas del vector suma (C)
se obtiene como suma de escalares, la suma de vectores es conmutativa pudiendo
escribir A + B = B +A.
Observamos en el esquema, que si trazamos un
paralelogramo tal que los sumandos sean dos lados del mismo, el vector suma, es el
vector que tiene como origen el origen común, y como extremo el vértice opuesto. A
este procedimiento se le conoce como: suma por el método del paralelogramo.
También puede observarse que trasladando al vector “A”, de forma que su origen

77. 77
coincida con el extremo de “B”, el vector suma es el vector que tiene como origen el
origen de “B”, y como extremo el extremo de “A”. A este procedimiento se le llama
suma por el método de la poligonal, dado que queda determinado un polígono (en
nuestro caso un triángulo).
Si debemos sumar más de dos vectores, puede demostrarse que se cumple la
asociativa:
A + B + C = (A + B) + C
RESTA DE VECTORES
Definimos la operación:
A - B = D tal que A = B + D (cumpliendo la propiedad uniforme).
De acuerdo al método de la poligonal:
Y por coordenadas cartesianas:

78. 78
Dx = Ax - Bx ; Dy = Ay - By
Observamos que las coordenadas del vector diferencia, son la diferencia de las
coordenadas del vector minuendo manos las del vector sustraendo.
PRODUCTO DE UN ESCALAR POR UN VECTOR
Si a las coordenadas de un vector A, las multiplicamos por un mismo escalar M,
obtenemos las coordenadas de un nuevo vector P, cuyas coordenadas son:
Px = M Ax ; Py = M Ay
donde el módulo del vector P es por el teorema de Pitágoras:
su argumento es de acuerdo a la definición de tangente trigonométrica:
Si representamos a estos vectores en un par de ejes
cartesianos, obtenemos:
Definimos entonces, el producto del escalar M y el
vector A como el vector P tal que el “valor” del vector
P es el “valor” del vector A multiplicado por el escalar
M, siendo iguales sus argumentos representando la

79. 79
operación como:
M A = P
Si el escalar M es positivo, el vector P tiene el mismo sentido que el vector A. En
cambio si el escalar M es negativo, el vector P tiene sentido opuesto que A.
VECTORES UNITARIOS
Los vectores unitarios, llamados versores, son vectores cuyo módulo vale uno.
El versor “A”, es un vector que tiene la dirección del vector A; su módulo es la unidad
y su notación es Â. Es la misma notación del vector, añadiéndole un acento circunflejo.
Podemos escribir que:
A = A Â
Trabajando en un espacio tridimensional, las coordenadas de un vector A respecto a
un sistema referencial (x; y; z) ortogonal, son una terna de números (Ax; Ay; Az).
Definiendo tres versores ortogonales (
) en los sentidos positivos de los ejes
(x; y; z) respectivamente. Multiplicando las
coordenadas del vector por sus
correspondientes versores, obtenemos las
componentes del vector en las direcciones de
los ejes del sistema referencial como
representamos.
Por lo antes dicho se cumple que:
SIGNO MATEMÁTICO DE UN VECTOR

80. 80
Como ya hemos visto, un vector con la dirección de la recta “r” orientada, puede
escribirse como el producto de un escalar por un versor como mostramos.
V = V
El escalar V puede ser positivo o negativo, dependiendo
de si el vector tiene igual sentido que el versor ere o sentido opuesto. En el caso
mostrado es positivo.
Si la recta “erre” está cambiando su dirección, por ejemplo respecto a un sistema
referencial ortogonal, el versor “erre” en cada instante es:
donde cada uno de los sumandos son las componentes del versor “erre” y los escalares
A; B y C serán positivos o negativos dependiendo de los ángulos que forme el versor
“erre” respecto a los ejes “x”; “y” y “z” del sistema referencial.
De acuerdo al teorema de Pitágoras debe cumplirse:
Por lo tanto el versor “erre” no tiene un signo asignado respecto al sistema referencial
“x”; “y”; “z” y tampoco lo tiene el vector V.
Resumiendo: un vector cuya dirección cambie respecto un sistema referencial, no
tiene un signo matemático asociado pero si lo tienen sus componentes.
PRODUCTO INTERNO (ESCALAR)
Como el vector A puede ser escrito como:
y observamos por el teorema de Pitágoras que los escalares de la relación anterior
cumplen:

81. 81
A2
= Ax
2
+ Ay
2
+ Az
2
se define el cuadrado de un vector, como el producto del vector por si mismo, de
manera que se cumpla:
A2
= A · A = A2
= Ax
2
+ Ay
2
+ Az
2
Observamos que este producto del vector A por el vector A, da como resultado un
escalar. Por este motivo, a este producto se le denomina producto escalar de vectores.
meñique en el sentido del primer factor (en nuestro ejemplo el vector A) y cerramos la
mano rotando los dedos antes mencionados el ángulo . El dedo pulgar queda indicando
el sentido del seudo-vector C.
En cambio si aplicamos la regla del tornillo, ubicamos un tornillo perpendicular al plano
determinado por los dos factores, y lo giramos en el sentido que se debe rotar el primer
factor sobre el segundo para que gire el ángulo . El sentido que avanza el tornillo, es el
sentido del seudo-vector producto,
Ejercicios
1 Dado el vector = (2, -1), determinar dos vectores equipolentes a ,
, sabiendo que A(1, -3) y D(2, 0).
2Calcula el valor de k sabiendo que el módulo del vector = (k, 3) es
5.
3Si es un vector de componentes (3,4), hallar un vector unitario de
su misma dirección y sentido.
4Dados los vértices de un triángulo A(1, 2), B( -3, 4) y C(-1, 3), hallar
las coordenadas del baricentro.
5 Hallar las coordenadas del punto C, sabiendo que B(2, -2) es el
punto medio de AC, A(-3, 1).

82. 82
6 Averiguar si están alineados los puntos: A(-2, -3), B(1, 0) y C(6, 5).
7Calcula las coordenadas de D para que el cuadrilátero de vértices:
A(-1, -2), B(4, -1), C(5, 2) y D; sea un paralelogramo.
8 Las coordenadas de los extremos del segmento AB son: A (2, -1) y
B(8, -4). Hallar las coordenadas del punto C que divide al segmento
AB en dos partes tales que AC es la mitad de CB.
9 Si el segmento AB de extremos A(1,3), B(7, 5), se divide en cuatro
partes iguales, ¿cuáles son las coordenadas de los puntos de división?
10 Hallar el simétrico del punto A(4, -2) respecto de M(2, 6).
Funciones
Conocer la realidad circundante al hombre es una de las funciones que se
propone el conocimiento científico y, por tanto, también la Matemática. En la realidad
suceden ciertos hechos y manifestaciones que resultan de interés para ser estudiados, a
los que llamamos fenómenos y situaciones. Para alguno de ellos disponemos de saber
matemático que permite su estudio y para otros todavía no.
Estudiaremos algunos fenómenos simples centrándonos principalmente en la
construcción matemática necesaria para entenderlos y representarlos. El proceso que
nos permite estudiar los fenómenos es el que llamamos modelización. Para simplificar
la explicación sobre la modelización, dividiremos el proceso en tres partes que pueden
darse en distintos momentos y el cual cada una de las partes puede retroalimentarse de
la otra.
- Parte inicial de la modelización o abordaje de la situación problemática o del
fenómeno: en esta parte hacemos un reconocimiento del fenómeno o situación
intelectual o experimentalmente, lo recortamos, lo simplificamos y lo aislamos
de la complejidad en la que aparece incluido. Identificamos las variables y
constantes que intervienen, reconocemos que se relacionan y luego mediante
experimentación, observación o supuestos acordes al funcionamiento del
fenómeno, decimos cómo es esa relación.

83. 83
- Parte central de la modelización o construcción del modelo matemático: esta
construcción consiste en encontrar la teoría y las herramientas matemáticas, que
en su totalidad llamamos modelo matemático, que describen la relación entre las
variables y permiten presentarla. Esto, en general, es complejo. Nosotros
veremos algunos casos donde la construcción del modelo consiste en defninir
una función matemática.
- Parte final de la modelización o explicación del fenómeno y de su evolución: el
modelo matemático nos permitirá comprender mejor el fenómeno en su
globalidad. Además la manipulación de los objetos matemáticos definidos nos
permitirá anticipar posibles alteraciones en el fenómeno y predecir su evolución
bajo las condiciones creadas para el modelo.
Funciones para modelizar
La idea de función está generalmente asociada a las ideas de dependencia y de
variabilidad. Por ejemplo, en el caso de la tarifa de remís, cuando un usuario viaja
quiere saber cuánto cuesta el viaje de acuerdo al kilometraje. Aquí se observa la
variabilidad del precio y de la cantidad de kilómetros, que serán entonces las
variables del problema, y cómo el precio depende de los kilómetros recorridos.
Sabiendo que la tarifa es de $1,10 el kilómetro, la fórmula matemática que
permitirá conocer el precio de un viaje es: P=1,10 x, siedo x la cantidad de
kilómetros recorridos.
Sin embargo tenemos que entender que esta fórmula no siempre resuelve el
problema real pues el remisero no nos cobra el resultado exacto de esa cuenta, sino
que es habitual que redondee.
Veamos otros ejemplos:
- Calcular el precio de una llamada telefónica sabiendo que cuesta $1,10 el
minuto.
- Calcular el precio de una caja de alfajores sabiendo que cada uno cuesta $1,10.
Una fórmula que permite hacer estos cálculos es la misma que antes: P=1,10x. sin
embargo la “x” cambia de acuerdo a los contextos. En los ejemplos, las situaciones
son diferentes e incluso lo son también las variables numéricas que intervienen. Por
ejemplo, en el caso de la caja de alfajores no parece tener sentido colocar dos
alfajores y medio. Uno de los intereses de la Matemática es estudiar “el objeto”

84. 84
independientemente de si ese objeto sirve para resolver el problema del remís, de la
llamada telefónica o del precio de la caja de alfajores. En este caso, el objeto está
formado por: cada uno de los conjuntos a los que pertenecen las variables y la
correspondencia establecida (en este caso a través de esa fórmula); en síntesis, el
objeto es la función. Informalmente, una función es una correspondencia entre
variables. Para definirla, necesitamos decir cuáles variables consideramos y cómo
vamos a establecer esa correspondencia.
Mas formalmente:
Función: Dados dos conjuntos A y B, que consideraremos no vacíos, una función de
A en B (que notamos f: A→B), es una correspondencia que a cada elemento de A le
hace corresponder un único elemento de B.
Esta definición no hace ver que para definir una función es necesario indicar los
conjuntos entre los cuales establecemos la correspondencia. El conjunto A, formado
por los elementos que tienen correspondiente, se llama dominio de la función, y B
se llama codominio. Al dominio lo notamos Dom f. Quiere decir que para definir
una función necesitamos tres componentes: un conjunto de partida o dominio A, un
conjunto de llegada o codominio B, y la correspondencia o regla de asignación entre
elementos de esos conjuntos. Al correspondiente de un elemento x de A lo
llamamos la imagen de x y la notamos f(x), si f es la función. Al conjunto del
codominio formado por todas las imágenes lo llamamos conjunto imagen de la
función f y lo notamos Im f.
La presentación de la correspondencia o de la regla de asignación entre elementos
puede aparecer en diferentes formas como las siguientes:
1.- Por diagramas de Venn. Esta presentación es útil cuando el conjunto A es finito.
Por ejemplo:

85. 85
Como vemos, esta correspondencia indicada por las flechas es una función de A en B
pues cada elemento del conjunto A tiene un único correspondiente en el conjunto B.
además vemos que 2 es la imagen de a y también b y 4 es la imagen de c. es decir que
dos elementos pueden compartir la misma imagen.
2.- Por una asignación coloquial. Por ejemplo, entre un conjunto A formado por
integrantes de una familia y un cojunto B formado por las integrantes mujeres de esa
familia, y un conjunto B formado por las integrantes mujeres de esa familia, se establece
la correspondencia dada por:
“..es hijo de…”. Todos hemos nadico de una mujer y además madre hay una sola, así
que esta correspondencia también puede ser considerada una función de A en B.
3.- Por asignación numérica sin fórmula para evaluar: A cada elemento del dominio se
le asigna un número que no se obtiene operando sobre cada valor del dominio. Por
ejemplo, siendo A el conjunto de los números reales y B= Z, el conjunto de los números
enteros, se define la correspondencia que a un número menor que cero le asigna -1 y si
no es menor que 0 le asigna 1. Esto se simboliza de la siguiente manera:
4.- Por tabla de valores: Cuando el dominio de una función es un conjunto finito y tiene
pocos elementos, la tabla de valores es una tabla en donde se listan los valores de la
variable dependiente y se colocan al mismo nivel sus correspondientes. Puede estar

86. 86
dispuesta en forma vertical u horizontal. La tabla de valores es útil para ver como es la
relación entre las variables en forma numérica.
5.- Por gráfico cartesiano: Usamos esta forma de presentación especialmente en los
casos en donde las variables pueden ser medidas y toman valores numéricos.
En el gráfico cartesiano se representan puntos. Cada punto está dado por un par
ordenado de números reales P=(x,y), donde x se llama abscisa de <p, y ordenada de P y
ambas se llaman coordenadas del punto P. el gráfico cartesiano consiste de:
-dos rectas que se intersecan perpendicularmente, una horizontal y otra vertical, que se
llaman ejes cartesianos.
- Para poder representar la recta numérica en cada eje hay que elegir un origen y una
unidad. El origen en ambos ejes es el punto de intersección de las rectas.
- La primera componente del par ordenado, la abscisa x, se representa sobre el eje
horizontal.
- La segunda componente del par ordenado, la ordenada y, se representa sobre el eje
vertical.
- Para determinar el punto P, se traza una paralela al eje vertical que contenga al punto
de abscisa x representando en el ítem anterior y una paralela al eje horizontal que
contenga al punto de ordenada representado en el ítem anterior. El punto P es el de
intersección de estas rectas trazadas.
Nótese que los puntos del plano que están sobre el eje de las abscisas (horizontal) tienen
coordenadas P=(x,0) mientras que los que están sobre el eje de las ordenadas (vertical)
son del tipo P=(0,y).
Cuando se tiene un gráfico que representa una función, sobre el eje horizontal están
representados los valores que toma la variable en el dominio y sobre el eje vertical sus

87. 87
imágenes por la correspondencia. Los puntos del plano representados tienen
coordenadas (x, f(x)). Por eso es que también se escribe y=f(x) para decir que la
ordenada del punto es la imagen de la abscisa.
Función Lineal
Funciones de proporcionalidad
Supongamos que estudiamos el movimiento de un auto que marcha a velocidad
constante por un camino recto y nos interesa saber cuáles son las distintas posiciones
del mismo a medida que transcurre el tiempo. Las magnitudes involucradas en este caso
son: la posición del auto respecto a un punto de referencia fijo y el tiempo. Si se sabe
que el auto tiene una velocidad constante de 80 Km/h podemos afirmar que por cada
hora que pase el auto va a aumentar su posición en 80 km respecto de la posición inicial
(Km 0), es decir:
. a t=0 h le corresponde P=0
. a t= 1 h le corresponde P= 80
. a t= 2 h le corresponde P= 80. 2 = 160
. a t = 3 h le corresponde P = 80 . 3 = 240
……………………………………………….
.a un t genérico le corresponde
De esta forma, la relación que describe la posición del automóvil es P = 80 t o bien
P(t)= 80t ( con ambas variables expresadas en las unidades correspondientes). La
función que queda definida por esa expresión algebraica es P: R≥0 R , P(t) = 80 t.

88. 88
Actividades
1)
El siguiente gráfico describe la altura de un líquido e función de la cantidad de vasitos
vertidos en una botella vacía. Proponer de qué forma debería ser la botella para que el
gráfico sea el que se da a continuación.
a) ¿Cuál es el nivel del líquido si se hecha medio vasito? ¿Y si se echan 2,3
vasitos? Justificar la respuesta.
b) Si la cantidad de vasitos aumenta de 2 a 6, ¿cuánto aumenta el nivel del líquido?
¿Por qué?
2) Se obtuvo la información de la posición P y el instante t en que un automóvil
atraviesa diferentes mojones en la ruta 2. Los datos relevados se muestran en la
tabla:
T (tiempo) P (posición)
0 hs 0 km
30 min 40 km
1 h 80 km

89. 89
2 hs 160 km
Estimar la posición a la que se encontraría el auto a las 3 hs, a las 5 hs y a las 6
horas y media.
c) ¿Por qué el ítem a) pide “estimar” y no “calcular exactamente”? ¿Se podría
haber respondido el ítem a) de manera exacta? ¿Qué supuesto adicional en el
contexto del problema se está considerando al responder a)?
2) Se tiene un barril de madera que tiene capacidad para 100 litros y sabemos que
vacío pesa 25 kg. Si un litro de aceite pesa 0,74 kg responder:
a) ¿Puede ser que el barril contenga 20 litros de aceite y que al apoyarlo en una
balanza ésta marque 39,8 kg? ¿Puede ser que contenga 43 litros y la balanza marque
55,8 kg?
b) ¿Cuál es el peso máximo que se puede obtener apoyando el barril sobre la
balanza?, ¿qué cantidad de litros tendría el barril en ese caso?
c) ¿cuántos litros habría que poner en el barril para que éste pese 106, 4 kg?
d) ¿cuál o cuáles de los siguientes gráficos puede/n corresponder a la situación
anterior? Justificar la elección. Dar una interpretación en términos de problema de
cada gráfico (a qué tipo de situación correspondería)
d) Se tiene otro barril de madera que se llena en simultáneo con el barril del caso
anterior. Se sabe que el nuevo barril vacío pesa 28 kg y que el aceite vertido en
el mismo pesa 0,65 kg por litro. ¿Para qué cantidad de litros vertidos se tiene
que ambos barriles pesan lo mismo? ¿Cuál es el planteo matemático al que esta
pregunta responde?

90. 90
3) Para la función lineal f: RR, f(x) = -4x + 2 se pide:
a) Indicar tres puntos de su gráfico.
b) Indicar tres puntos que no pertenezcan a su gráfico.
c) Marcar en la recta que determina la función, los puntos donde la gráfica corta a cada
uno de los ejes (si los tiene). Indicar los valores de sus coordenadas.
d) Hallar los conjuntos de positividad y de negatividad (es decir todos los valores reales
de x que verifican f(x) <0 y f(x)<0 respectivamente).
e) Indicar si 5 es un elemento de la imagen de f. Justificar.
f) Identificar Im f.
g) Hallar la intersección de la recta hallada con la que se obtiene graficando la función
g: RR que cumpla:
a) su pendiente es 3 y contiene al punto (-1;2). ¿Es única?
b) su pendiente es 0 y contiene al punto (4;7).
c) su pendiente es -2/3 y contiene al punto (4;-1).
4) Para cada una de las rectas determinadas por las funciones lineales dadas, se pide:
a) Hallar una recta paralela a ella.
b) Hallar la recta paralela que contenga al punto (7;0).
c) Hallar cualquier recta perpendicular a la primera.
d) Hallar la recta perpendicular que contenga al punto (3;-2).
Funciones definidas explícitamente

91. 91
Una función escalar, puede ser definida por cualquier recurso que permita hallar,
para cada punto de un dominio determinado, el valor de la imagen correspondiente.
El método más común es, como ya se ha dicho, dar una regla, o varias, que
permitan determinar f(x), conocido x, directamente mediante una sustitución numérica.
Es el caso de las funciones definidas en forma explícita.
Por ejemplo, si f: xx2
+ senx, la función f está definida explícitamente por la
expresión anterior.
Suelen llamarse funciones trascendentes, las funciones exponenciales como
g: xln x (logex), las trigonométricas, etc.
Si bien la terminología anterior es útil para introducir el tema, el concepto
moderno de función lleva a prescindir de esquemas rígidos y se prefiere dar amplia
libertad para la construcción de funciones, con la única exigencia de respetar la
definición.
Presentaremos, a continuación, algunas funciones definidas en forma explícita,
cuyo uso es muy común en el cálculo elemental.
Se aconseja, sin embargo, al lector, “crear” sus propias funciones, hasta
conseguir manejarlas con soltura.
Funciones más usuales:
1) Función constante
F es una función constante si y sólo si .
Su gráfico es una recta horizontal
Función idéntica
F es la función idéntica sobre R si y sólo si cada número real admite como imagen ese
mismo número real. Es decir,

92. 92
Su gráfico es la recta que incluye a la bisectriz del primer cuadrante.
Función valor absoluto
F es la función módulo o valor absoluto si y sólo si .
Su gráfico está formado por las bisectrices del primer y segundo cuadrantes, pues los
valores de f son no negativos.
Función signo
La función signo está definida por la regla siguiente:
. Su dominio es el conjunto de los números reales del cual se excluye el
cero. Su gráfico está formado por dos semirrectas horizontales, cada una sin su origen.

93. 93
Función parte entera
Se llama parte entera de un número real x al menor de los números enteros entre los
cuales está comprendido si x no es número entero y al mismo número x si éste es
entero.
O sea parte entera del número real x es el número entero e si y sólo si
Si x es número real, su parte entera se designa
Así:
Ent (1,6) = 1; ent (0,4) = 0; ent (-3,7) = -4; ent(-0,2) = -1.etc.
La función “parte entera” o “piso”, es la que a cada número real les asigna, como
imagen, su parte entera.
Es decir,
Su gráfico es escalonado, formado por segmentos horizontales a los cuales no les
pertenece el extremo derecho.
Función mantisa
Así:

94. 94
Función Polínomica de segundo grado
Las funciones polinómicas de segundo grado se llaman funciones cuadráticas y son del
tipo:
Dónde donde a ≠ 0 , siendo su gráfica una parábola.
Las características generales de las funciones polinómicas de segundo grado son:
1) El dominio de las funciones cuadráticas es R.
2) Tiene un eje de simetría cuya fórmula es:
3) El vértice de la parábola es:

95. 95
4) Corta al eje X en dos puntos, uno o ninguno, según el número de raíces reales
de ax2
+ bx + c = 0 .
5) Corta el eje Y en el punto (0, c) .
6) El vértice es un mínimo si a > 0 y un máximo si a < 0 .
7) Es concava si a > 0 y convexa si a < 0 .
8) Al aumentar a en valor absoluto, la parábola se hace más estrecha.
Tipos de funciones cuadráticas
En una función cuadrática f(x) = ax2
+ bx + c , con a ≠ 0 .
Si b = 0 y c = 0
La función f(x) = ax2
tiene su vértice en el punto (0, 0) y su eje de simetría es el
eje Y.

96. 96
Si b = 0 y c ≠ 0
La función f(x) = ax2
+ c tiene su vértice en el punto (0, c) y su eje de simetría es
el eje Y.
Si b ≠ 0 y c = 0
La función f(x) = ax2
+ bx tiene su vértice y su eje de simetría en:

97. 97
Representa graficamente la función: f(x) = x2
- 5x + 6
1) Puntos de corte con los ejes:
Para x = 0 tenemos que f(0) = 6 luego el punto de corte con el eje Y es (0, 6) .
Para y = 0 tenemos que 0 = x2
- 5x + 6 así que resolvemos la ecuación de segundo
grado:

98. 98
Por lo tanto, los puntos de corte con el eje X son (2, 0) y (3, 0) .
2) Vértice de la parábola:
También podemos hacer yv = f(5/2)
3) Máximos o mínimos:
Como a > 0 entonces tenemos un mínimo, que coincide con el vértice.

99. 99
4) Crecimiento o decrecimiento:
Como a > 0, tenemos que la función es decreciente en el intervalo (- ∞, 5/2) y
creciente en el intervalo (5/2, + ∞).
5) Concavidad o convexidad:
Como a > 0 la función es concava en todo su dominio.
6) Tabla de valores:
Construimos una tabla de valores con los puntos de corte con los ejes, el vértice y
otros puntos alrededor de él.

100. 100
Representa graficamente la función: f(x) = - x2
+ 5x - 6
1) Puntos de corte con los ejes:
Para x = 0 tenemos que f(0) = - 6 luego el punto de corte con el eje Y es (0, - 6) .
Para y = 0 tenemos que 0 = - x2
+ 5x - 6 así que resolvemos la ecuación de
segundo grado, siendo sus raíces x = 2 y x = 3.
Por lo tanto, los puntos de corte con el eje X son (2, 0) y (3, 0) .
2) Vértice de la parábola:

101. 101
También podemos hacer yv = f(5/2)
3) Máximos o mínimos:
Como a < 0 entonces tenemos un máximo, que coincide con el vértice.
4) Crecimiento o decrecimiento:
Como a < 0, tenemos que la función es creciente en el intervalo (- ∞, 5/2) y
decreciente en el intervalo (5/2, + ∞).
5) Concavidad o convexidad:
Como a < 0 la función es convexa en todo su dominio.
6) Tabla de valores:
Construimos una tabla de valores con los puntos de corte con los ejes, el vértice y
otros puntos alrededor de él.

102. 102
Dada la siguiente gráfica, estudia todas sus características. Es decir, completa los
siguientes apartados:
1) Tipo de función.
2) Dominio.
3) Recorrido o imagen.

103. 103
4) Continuidad.
5) Periodicidad.
6) Simetrías.
7) Asíntotas.
8) Corte con los ejes.
9) Monotonía.
10) Máximos y mínimos relativos.
11) Curvatura y puntos de inflexión.
12) Acotación.

104. 104
1) Tipo de función: es una función polinómica de grado 2, es decir, es una función
cuadrática. Es una parábola.
2) Dominio: como es una función polinómica, Dom(f) = R.
3) Recorrido o imagen: Im(f) = [0 , ∞)
4) Continuidad: es continua en todo R, es decir, la función f está bien definida para
todo valor real.
5) Periodicidad: no es periódica.
6) Simetría:
f(-x) = 4(-x)2
- 4x + 1 = 4x2
- 4x + 1

105. 105
f(-x) ≠ f(x) , por lo que no tiene simetría par.
f(-x) ≠ - f(x) , por lo que no tiene simetría impar.
La función f no es simétrica, como además se ve en la gráfica.
7) Asíntotas: no tiene asíntotas.
8) Corte con los ejes:
• x = 0: y = 4x2
+ 4x + 1 ⇒ y = 1 ⇒ A = (0 , 1)
• y = 0: 4x2
+ 4x + 1 = 0
B = (-1/2 ,0)
Signo: es positiva en todo R.
9) Monotonía:
• Creciente en: (-1/2 , ∞)

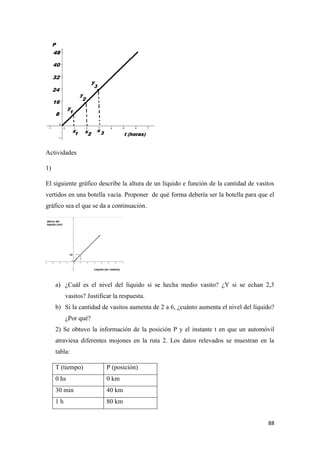
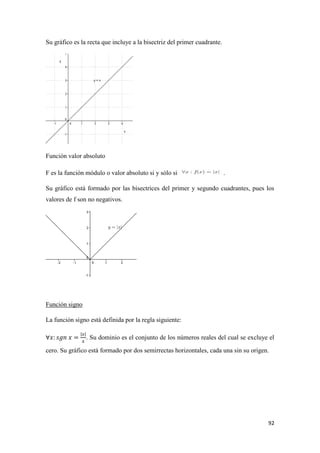
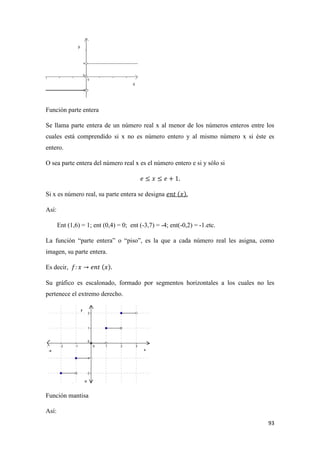
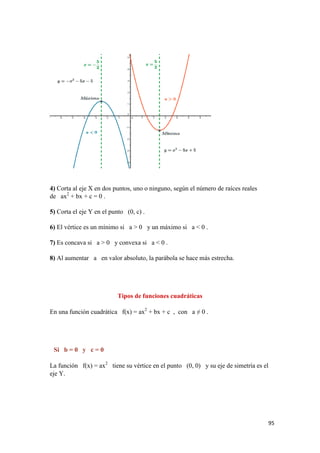
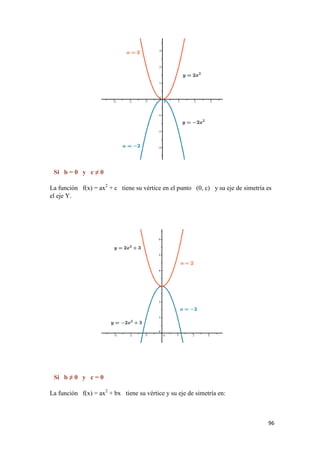
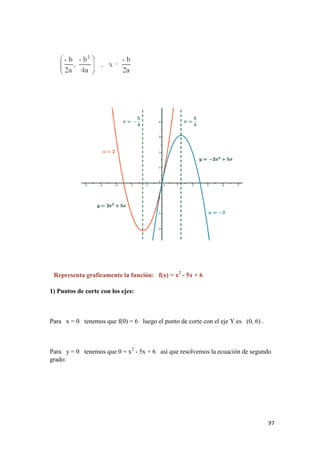
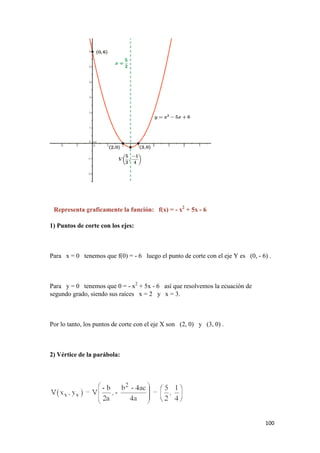
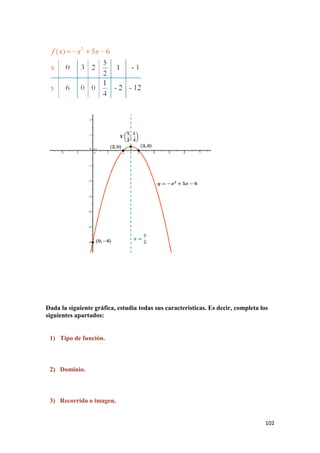
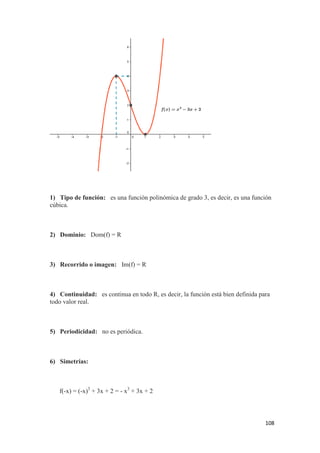
106. 106
• Decreciente en: (-∞ , -1/2)
10) Máximos y mínimos relativos: tiene un mínimo relativo en el punto (-1/2 , 0).
11) Curvatura y puntos de inflexión:
Es una función cóncava en todo R.
No tiene puntos de inflexión.
12) Acotación:
Por la gráfica, vemos que f no tiene cotas superiores.
Observando la gráfica vemos que las cotas inferiores de la función son: (-∞ , 0].
De todas las cotas inferiores, la más grande es y = 0 , por lo que inf(f) = 0.
Como 0 ∈ Im(f) , tenemos que y = 0 es el mínimo absoluto de la función.
La función f no está acotada, ya que sólo está acotada inferiormente.

107. 107
Estudio completo de funciones. Ejercicios resueltos.
Dada la siguiente gráfica, estudia todas sus características. Es decir, completa los
siguientes apartados:
1) Tipo de función.
2) Dominio.
3) Recorrido o imagen.
4) Continuidad.
5) Periodicidad.
6) Simetrías.
7) Asíntotas.
8) Corte con los ejes.
9) Monotonía.
10) Máximos y mínimos relativos.
11) Curvatura y puntos de inflexión.
12) Acotación.

108. 108
1) Tipo de función: es una función polinómica de grado 3, es decir, es una función
cúbica.
2) Dominio: Dom(f) = R
3) Recorrido o imagen: Im(f) = R
4) Continuidad: es continua en todo R, es decir, la función está bien definida para
todo valor real.
5) Periodicidad: no es periódica.
6) Simetrías:
f(-x) = (-x)3
+ 3x + 2 = - x3
+ 3x + 2

109. 109
f(-x) ≠ f(x) , por lo que no tiene simetría par.
f(-x) ≠ - f(x) , por lo que no tiene simetría impar.
La función f no es simétrica, como además se ve en la gráfica.
7) Asíntotas: no tiene asíntotas.
8) Corte con los ejes:
• x = 0: y = x3
- 3x + 2 ⇒ y = 2 ⇒ A = (0 , 2)
• y = 0: x3
- 3x + 2 = 0
Calculamos las raíces por el método de Ruffini: los divisores del término
independiente son ±1 , ±2.
x3
- 3x + 2 = (x - 1)(x2
+ x - 2) = 0 ⇔ x = 1 , x2
+ x - 2 = 0

110. 110
Tenemos dos puntos de corte con el eje OX: B = (1 , 0) , C = (-2 , 0)
Signo de la función:
• Positiva en: (-2 , ∞)
• Negativa en: (-∞ , -2)
9) Monotonía:
• Creciente en: (-∞ , -1) ∪ (1 , ∞)
• Decreciente en: (-1 , 1)
10) Máximos y mínimos relativos:
Tiene un máximo relativo en el punto (-1 , 4).
Tiene un mínimo relativo en el punto (1 , 0).
11) Curvatura y puntos de inflexión:
• Convexa en: (-∞ , 0).

111. 111
• Cóncava en: (0 , ∞).
Tiene un punto de inflexión en (0 , 2).
12) Acotación:
Esta función no está acotada, ni superior, ni inferiormente. Por tanto, no está
acotada.
ECUACIONES
Se darán algunas definiciones.
Identidad Algebraica: Es una igualdad entre dos expresiones algebraicas que es
verificada cualesquiera sean los valores atribuidos a las variables (letras) contenidas en
las dos expresiones, excluidos aquellos valores para los cuales al menos una de las dos
expresiones algebraicas pierden significado. También se llama igualdad incondicional.
Ejemplo: (x + y)2
= x2
+ y2
+ 2xy es una identidad.
Ecuación Algebraica: Es una igualdad entre dos expresiones algebraicas que es
verificada solamente para valores particulares de las variables (letras) contenidas en las
dos expresiones.
Incógnitas: Son las variables (letras) que aparecen en una ecuación algebraica.
Miembros de la ecuación: Son las dos expresiones algebraicas que forman la ecuación.
Se llama primer miembro a la expresión algebraica que se encuentra a la izquierda del
signo igual y segundo miembro al que se encuentra a la derecha.
Solución de la Ecuación: son los valores que, atribuidos a las variables incógnitas,
producen una igualdad entre los dos miembros de la ecuación.
Resolver una Ecuación: consiste en hallar todas las soluciones de la ecuación dada.
Ejemplos: la ecuación x +1 = 0 tiene una sola ecuación x = 1 ; la ecuación x = x tiene
infinitas soluciones al ser una identidad; la ecuación x2
= -1 no tiene ninguna solución
real.
Una ecuación puede clasificarse, de acuerdo al número de incógnitas en:
 Ecuación con una incógnita;
 Ecuación con dos incógnitas, etc.
A un conjunto de dos o más ecuaciones (igualdades a satisfacerse) se llama sistema de
ecuaciones.
Se puede hablar de un sistema de n ecuaciones con m incógnitas (n,m Є N)

112. 112
Una ecuación algebraica, en la incógnita x, se clasifica en:
1) Entera: cuando los dos miembros de la ecuación son expresiones algebraicas
enteras respecto de la letra x.
2) Fraccionaria: cuando al menos uno de los dos miembros de la ecuación son
expresiones algebraicas fraccionarias que contienen la incógnita en el
denominador.
3) Irracional: cuando al menos uno de los dos miembros de la ecuación son
expresiones algebraicas que contienen la incógnita como radicando.
Ejemplos:
a) a.x + b = 0, se llama ecuación de primer grado en la
incógnita x. Es una ecuación algebraica entera con una incógnita.
b) .ax2
+ bx + c = 0, con a, b, c Є R, a ≠ 0 se llama ecuación de segundo
grado en la incógnita x. Es una ecuación algebraica entera con una
incógnita.
c) Un sistema de dos ecuaciones con dos incógnitas es el dado por:
Con
’
d) es una ecuación fraccionaria en la incógnita x.
e) es una ecuación Irracional en la incógnita x.
Una ecuación algebraica puede clasificarse en:
 Numérica: cuando contiene sólo números excepto de la incógnita;
 Literal o paramétrica: cuando contiene letras o parámetros que representan
números bien determinados además de la incógnita.
Ejemplos: la ecuación x +1 = 0 es numérica y tiene por única solución x=-1; la ecuación
x + m = 0 y tiene por única solución x = -
R.
Ecuaciones equivalentes: dos ecuaciones son equivalentes algebraicas en la misma
incógnita cuando todas las soluciones de la primera ecuación son también soluciones de
la segunda ecuación y, viceversa, todas las soluciones de la segunda ecuación son
también soluciones de la primera.
Ejemplo: se tiene x = 3 es solución de las dos ecuaciones x – 3 = 0 y x2
– 9 = 0; en
cambio x = -3 es solución de la segunda ecuación pero no de la primera. Por lo tanto,
estas ecuaciones no son equivalentes.
Proposición: dos ecuaciones equivalentes a una tercera son equivalentes si.
Una ecuación o sistema de ecuaciones puede clasificarse en:
 Compatible o Determinado: cuando tiene un número finito de soluciones.
 Indeterminado: cuando tiene infinitas soluciones.
 Incompatible: cuando no existe ninguna solución.


113. 113
METODOLOGÍA PARA RESOLVER UNA ECUACIÓN.
Debido al hecho de que dos ecuaciones equivalentes tienen las mismas soluciones, es
claro que cuando se quiere resolver una ecuación, se puede resolver una cualquiera que
sea equivalente a la dada; y por lo tanto será particularmente muy ventajoso cuando la
segunda ecuación se presente en una forma más simple que la primera. El procedimiento
que se seguirá para resolver una ecuación consistirá en la transformación de la ecuación
en otra equivalente pero más simple, y así sucesivamente, hasta arribar a una ecuación
equivalente a la dada, de la cual se sap con facilidad encontrar sus soluciones.
Por lo tanto, se comprende que es esencial ver cuáles son las operaciones que se pueden
hacer sobre una ecuación para transformarla en otra equivalente. Se tienen las siguientes
propiedades.
 Principio de la Adición: si a ambos miembros de una ecuación se le suma un
mismo número real, o una misma expresión algebraica en la incógnita x que se
pueda calcular para cada valor de la x, se obtiene una ecuación equivalente a la
dada.
Ejemplo: la ecuación 2x – 6 = 0 es equivalente a la ecuación 2x = 6, que se obtiene
sumando a ambos miembros el número real 6.
Observación. Si la expresión que se suma no se puede calcular para cada valor de la x,
entonces puede suceder que las dos ecuaciones no sean equivalentes. Por ejemplo, la
ecuación x2
= 4, que tiene por soluciones x = -2 y x = 2, no es equivalente a la ecuación
.x2
+ . 1 . = 4 + . 1 .
x – 2 x – 2
pues la expresión . 1 . no está definida para x = 2.
.x – 2
 Principio de la Multiplicación: si a ambos miembros de una ecuación se le
multiplica por un mismo número real distinto de cero, o una misma expresión
algebraica en la incógnita x que se pueda calcular para cada valor de la x y que
no se anule jamás, se obtiene una ecuación equivalente a la dada.
 Ejemplo: la ecuación 2x = 6 es equivalente a la ecuación x = 3, que se obtiene
multiplicando ambos miembros por el mismo número real ½.
ECUACIÓN DE PRIMER GRADO EN UNA VARIABLE.
Definición: se llama ecuación de primer grado en la incógnita x a la siguiente
expresión:
∈ ∈
Teorema: la ecuación de primer grado en la incógnita x tiene una única solución dada
por:
∈
.a
Demostración: Se tienen las siguientes equivalencias:
.ax + b = 0 ax = - b x = - b

114. 114
a
Observación : La ecuación ax + b = 0 (a,b Є R) con a ≠ 0 posee las siguientes
particularidades:
1) tiene ifinitas soluciones x Є R cuando b = 0.
2) No tiene soluciones cuando b≠ 0.
El estudio de la ecuación ax + b = 0 (con a,b Є R) se puede resumir en el
siguiente cuadro:
PROBLEMAS DE APLICACIÓN:
Numerosos problemas se pueden llevar a la resolución de ecuaciones, en particular, de
las ecuaciones de primer grado.
En numerosas aplicaciones, interviene la noción de porcentaje. En muchos casos, es
muy útil saber expresar el porcentaje como una fracción o número decimal, por
ejemplo:
10 % = 10 = 1 = 0,10 15 % = 15 = 3 = 0,15
100 10 100 20
50 % = 50 = 1 = 0,50 100% = 100 = 10 = 1
100 2 100 10
Ejemplos:
 Un padre tiene 40 años y su hijo 10 años. En cuantos años la edad del padre será
el triple de la edad del hijo?.
Solución.: Se indica con x la cantidad de años que deben transcurrir (incógnita del
problema) para que la edad del padre sea igual al triplo de la edad del hijo Entonces
se puede plantear la siguiente ecuación de primer grado:
X + 40 = 3. ( x + 10)
X + 40= 3.x + 3.10
X + 40= 3.x + 30
X – x +40 = 3.x –x +30
40= 2.x +30
40 –30 = 2.x +30 – 30

115. 115
10= 2.x
10 : 2 = 2.x :2
5 = x
Dentro de 5 años el padre y el hijo tendrán 45 y 15 años. ( 45 = 3.15)
Ejemplos:
Cuando ax2
+bx + c = 0 x2
– 4x + 3 = 0
Para hallar las raíces aplicamos la fórmula.
Cuando ax2
+ bx= 0 x2
+ 5x =0 x1 = 0 x2 = - 5 = -5
1
o bien sacando factor común x x . ( x + 5 ) = 0
una raiz ya es 0 x1 = 0 por en el producto igual a cero uno de los factores
debe ser 0.
Luego x +5 = 0 entonces x = -5 ; x2 = -5
X1 = 5
Cuando ax2
+ c = 0 2x2
–50 = 0 x = +- 50 = +- 25
2
x2= -5

116. 116

117. 117
PROBLEMAS CON FUNCIONES CUADRÁTICAS
PARA TODOS LOS EJERCICIOS DE ECUACIONES PUEDES VERIFICAR CON
EL USO DE GEOGEBRA
1) Para alambrar un campo rectangular se necesitan 100 m de alambre. ¿Cómo
varía el área del campo en función del ancho?
2) Qué área tendría el campo si mide: a) 20,5 m de ancho; b) 30 m de ancho; c) 50
m de ancho.
3) Representa gráficamente las siguientes funciones, halla previamente las raíces,
el eje de simetría y el vértice.
a) f(x) = x2
– 4x + 3
b) f(x) = x2
– 2x +1
4) El propietario de un campo quiere plantar una huerta de 500 m2
, de forma
rectangular y pegada al río. Para evitar destrozos de las vacas decide cerrarlo – salvo el
lado que da sobre el río-, utilizando 70 m de tela metálica. ¿Cuánto deben medir los
lados?
El método de Cardano es un método para hallar analíticamente las raíces de cualquier
ecuación cúbica de la forma: siendo . Si bien el método
general permite obtener tanto soluciones reales como imaginarias, existe una forma
simplificada que permite obtener rápidamente las soluciones reales.
Si las raíces de la ecuación son todas reales, cada una de ellas se obtienen
como:
∈
Para calcular se deben calcular previamente:

118. 118
Y finalmente se obtiene:
∈
Ejemplo:
Resolver por el método de Cardano la ecuación cúbica siguiente:
Tenemos que por lo tanto:
Para
⇒
Para
⇒
Para
⇒
Aclaración: Para usar este método los ángulos deben expresarse en radianes.
SISTEMAS DE ECUACIONES DE PRIMER GRADO CON DOS INCÓGNITAS.
ECUACIÓN DE PRIMER GRADO CON DOS INCÓGNITAS
La ecuación de primer grado con una incógnita tiene una sola raíz. El conjunto solución
es unitario.
La ecuación de primer grado con dos incógnitas tiene siempre infinitas soluciones, es
decir, existen siempre infinitos pares o duplas de números que sustituidos
respectivamente en las incógnitas x,y satisfacen la ecuación.

119. 119
Ejemplo:
(1) 2 x – y = 5 => 2 x – y – 5 = 0
Para encontrar los pares de valores (x,y) que verifican la ecuación (1) conviene despejar
y. X Y (x,y)
-y = 5 – 2x 0 2.0-5= -5 (0,-5)
y = 2x – 5 1 2.1-5= -3 (1,-3)
2 2.2-5= -1 (2,-1)
A cada valor de x corresponde un valor de y. 3 2.3-5 = 1 (3, 1)
4 2.4-5 = 3 (4, 3)
5 2.5-5 = 5 (5, 5)
Cada par (x,y) que verifica la igualdad (1) es una raíz de la ecuación.
La ecuación de primer grado con dos incógnitas tiene infinitas soluciones.
S = {(0,-5) ; (1,-3); (2,-1)....................}
El conjunto solución está representado por el conjunto de puntos de la recta y = 2x –5.
Las coordenadas de cualquier punto de la recta verifican la ecuación.
SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS
Consideremos un conjunto de dos ecuaciones con dos incógnitas:
Ejemplo 1
2x – y = 0 (1)
x + y – 9 = 0 (2)
El conjunto de estas dos ecuaciones se llama sistema de dos ecuaciones con dos
incógnitas. Como ambas ecuaciones son de primer grado, decimos que es un sistema de
dos ecuaciones de primer grado con dos incógnitas. Para indicar que forman un sistema,
se abarcan con una llave.
RESOLUCIÓN DE UN SISTEMA DE DOS ECUACIONES CON DOS
INCÓGNITAS

120. 120
Resolver un sistema de dos ecuaciones con dos incógnitas significa hallar el conjunto de
raíces comunes, es decir, la intersección de los conjuntos solución de ambas ecuaciones.
Hallamos las raíces de la ecuación (1) Hallamos las raíces de la ecuación (2) despe-
despejando y: x y jando y: x y
2x – y = 0 -4 -8 x + y – 9 = 0 -4 13
y = 2x -3 -6 y = 9 – x -3 12
-2 -4 -2 11
-1 -2 -1 10
0 0 0 9
1 2 1 8
2 4 2 7
3 6 3 6
4 8 4 5
Escribimos los conjuntos solución S1 y S2.
S1 = {....(-4,-8), (-3,-6), (-2,-4), (-1,-2), (0,0), (1,2), (2,4), (3,6), (4,8),......}
S2 = {.....(-413), (-3, 12), (-2,11), (-1,10), (0,9), (1,8), (2,7), (3,6), (4,5),....}
S = S1  S2 = { (3,6)}
Gráficamente:
Como la representación gráfica de una ecuación de primer grado con dos incógnitas es
una recta, es suficiente hallar dos puntos, o bien determinarla pendiente y el punto en
que corta al eje y ( ordenada al origen).
En este caso las rectas se cortan en un punto.
El conjunto solución es unitario. Existe un solo par de valores (x,y) que verifica la
ecuación.
X = 3 Y = 6

121. 121
Decimos que el sistema es determinado.
Ejemplo 2
X – y = 3 y = x – 3 y = x - 3
2x – 2y – 6 = 0 y = 2x – 6 y = x - 3
2
y = x –3 y = 2x –6
2
x y
-1 -1 –3= -4
0 0 –3 = -3
1 1 – 3 = -2
2 2 – 3 = -1
3 3 – 3 = 0
4 4 – 3 = 1
x y
-1 2.-1 –6 = -4
2
0 2.0 –6 = -3
2
1 2.1 – 6 = -2
2
2 2.2 –6 = -1
2
3 2.3 – 6 = 0
2
4 2.4 – 6 = 1
2

122. 122
La pendiente es 1. La ordenada al origen es –3.
S1 = { ....(-1,-4), (0,-3), (1,-2), (3,0), (4,1),....}
S2 = { ....(-1,-4), (0,-3), (1,-2), (3,0), (4,1),....}
Los conjuntos solución son iguales
S1 S2 = S1
Las rectas que representan ambas ecuaciones coinciden.
El conjunto solución del sistema tiene infinitos pares que satisfacen ambas ecuaciones.
Se dice que el sistema es indeterminado.
Ejemplo 3
X – y – 3 = 0 y = x – 3 y = x - 3
2x – 2y = -4 y = 2x + 4 y = x + 2
2
y = x – 3 y = x + 2
x y . . x y .
-3 -3 –3 = -6 -3 -3 +2 = -1
-2 -2 –3 = -5 -2 –2 +2 = 0
-1 -1 –3 = -4 -1 –1 +2 = 1
0 0 – 3 = -3 0 0 + 2 = 2
1 1 – 3 = -2 1 1 + 2 = 3
2 2 – 3 = -1 2 2+ 2 = 4
3 3 – 3 = 0 3 3 + 2 = 5
S1 = { ...(-3,-6), (-2 ,-5 ), (-1 ,-4 ), (0,-3), (1,-2), (2,-1), (3,0),.....}

123. 123
S2= {...(-3,-1), (-2,0), (-1,1), (0,2), (1,3), (2,4), (3,5),.......}
Los conjuntos solución no tienen elementos comunes.
S = S1 S2 = 
El conjunto solución del sistema es vacío. Ningún par (x,y) satisface ambas ecuaciones.
Se dice que el sistema es incompatible.
MÉTODOS DE RESOLUCIÓN DE UN SISTEMA DE DOS ECUACIONES DE
PRIMER GRADO CON DOS INCÓGNITAS.
Existen diversos métodos para resolver un sistema de dos ecuaciones con dos
incógnitas.
En los ejemplos anteriores has representado gráficamente el conjunto solución. La
representación gráfica de las ecuaciones constituye uno de los procedimientos para
encontrar el conjunto solución.
Generalmente se procede de la siguiente manera:
1. Se elimina una de las incógnitas para transformar el sistema de dos ecuaciones
con dos incógnitas en una ecuación de primer grado con una incógnita.
2. Se resuelve la ecuación de primer grado con una incógnita por los métodos
conocidos.
3. Se reemplaza la raíz hallada en una de las ecuaciones del sistema y la expresión
resultante permite calcular la otra incógnita.
Observa que el nombre de cada uno de los métodos deriva del recurso utilizado para
eliminar una de las incógnitas.
1. Sustitución
Sea el sistema:
(1) 4x + y = 4
(2) 2x – 3y = -5
1. Despejamos y en la primera ecuación
Y = -4 x + 4 (1)
Sustituimos el valor de y en la segunda ecuación: 2 x – 3 y = -5
2 x – 3(-4 x + 4) = -5
Hemos obtenido por sustitución una ecuación de primer grado con una incógnita.
2. Resolvemos la ecuación obtenida:
2 x + 12 x – 12 = -5
14 x = -5 + 12
x = 7 x = 1
14 2
3. Reemplazando el valor de x en la igualdad (1).
Y = -4 x + 4
Y = -4 . 1 + 4
2
Resolvemos: y = -2 + 4 y = 2
S = (1 , 2)

124. 124
2
2. Igualación
Sea el sistema:
2 x + y = -1
5 x + 3 y = -5
1 . Despejamos x en ambas ecuaciones:
De la primera: x = -1 –y (1)
2
De la segunda: x = -5 –3 y (2)
5
Igualamos los dos valores de x
- 1 – y = -5 – 3 y
2 5
Hemos obtenido por igualación una ecuación de primer grado con una incógnita.
2. Resolvemos la ecuación obtenida:
-5 – 5 y = -10 – 6 y
-5 y + 6 y = -10 + 5
y = -5
3. Reemplazamos el valor de y en la igualdad (1) ( o en la (2) ):
X = - 1 - y
2
Resolvemos : X = - 1 – (- 5)
2
X = 2
S = { (2, -5) } x = 2 y = -5
3. Sumas o restas (reducción)
a) Sea el sistema:
X + 2 y = 4
- x – 3 y = - 7
1. Es fácil ver que puede eliminarse la incógnita x sumando miembro a
miembro
X + 2 y = 4
- x – 3 y = -7
- y = - 3
Obtenemos una ecuación de primer grado en y.
2. Resolvemos: y = 3

125. 125
3. Reemplazamos y en la primera ecuación (o en la segunda).
X + 2.3 =4
X = 4 –6 x = -2
4. Determinantes
Este método consiste en ordenar los coeficientes y el término independiente, uno a uno
los de la primera ecuación con los de la segunda. Una vez realizado esto, pasamos a la
siguiente
Definición: Se llama determinante de la matriz cuadrada de orden 2 al siguiente número
real: a b
|M| = = ad - bc
c d
que resulta ser el producto de los coeficientes de la diagonal principal menos el
producto de los coeficientes de la diagonal secundaria.
Dados estos conceptos, se procede del siguiente modo para resolver el sistema:
1) La incógnita x se obtiene como una fracción teniendo por denominador el
determinante de la matriz de los coeficientes del sistema y por numerador, el
determinante que se obtiene al sustituir la columna de la matriz que corresponde
a los coeficientes de la x por la de los términos independientes, es decir:
. c b
x = c’ b’ = cb’ – bc’
a b ab’ – ba’
a’ b’
2) La incógnita y se obtiene como una fracción teniendo por denominador el
determinante de la matriz de los coeficientes del sistema y por numerador, el
determinante que se obtiene al sustituir la columna de la matriz que corresponde
a los coeficientes de la a y por la de los términos independientes, es decir:
. a c
Y = a’ c’ = ac’ – ca’
. a b ab’ – ba’
. a’ b’
Ejemplo: La solución del sistema
5 x – y = 5
-2x + 3y = 11
viene dada por:
5 -1
x = 11 3 = 5.3 - 11.(-1) = 26 = 2;
5 -1 5.3 – (-2).(-1) 13
-2 3
5 5
y = -2 11 = 5.11 – (-2).5 = 65 = 5

126. 126
5 -1 5.3 – (-2).(-1) 13
-2 3
x = 2 y = 5
PRÁCTICO DE ECUACIONES Y SISTEMAS DE ECUACIONES
1) La suma de dos números impares consecutivos es 548. ¿Cuáles son estos dos
números?.
2) El segundo número de la combinación para abrir una caja fuerte es el doble del
primero y tercer número es un cuarto del segundo. Si la suma de los tres
números es 42, ¿Cuál es la combinación?.
3) Resuelve y representa los siguientes sistemas de ecuaciones:
a) 2 x – y = 0 b) x + y = -1 c) 2 x + y = 5
x + y = 9 2x – 2y = -6 4x + 2 y = -4
Taller de Resolución de Problemas: Aplicaciones a Ingeniería
Materia de apoyo para ingreso a carreras de Ingenierías
Propuesta para Ingreso a
Pasos a seguir para resolver problemas aplicados:
1) Si el problema se enuncia por escrito, léalo cuidadosamente varias
veces y piense en los datos que se dan, junto con la cantidad
desconocida que se debe encontrar.
2) Denote la cantidad desconocida mediante una letra. ¡Éste es uno de los
pasos cruciales en la solución!. Las frases que contienen palabras como
“qué”, “encuentre”, “cuánto”, “a qué distancia” o “cuándo”, nos indican la
cantidad desconocida.
3) Si es posible, trace un croquis con las anotaciones apropiadas.
4) Haga una lista de los datos conocidos, junto con todas las relaciones
que contienen la cantidad desconocida. A veces se pueden describir

127. 127
relaciones por medio de una ecuación en la que aparecen enunciados
escritos, en vez de letras o números, en uno o en ambos lados del signo
igual.
5) Después de analizar la lista del paso 4 y tal vez leyendo el problema
varias veces, formule una ecuación que describa precisamente lo
enunciado en palabras.
6) Resuelva la ecuación formulada en el paso 5.
7) Verifique las soluciones obtenidas en el paso 6 refiriéndolas al
enunciado original del problema. Observe cuidadosamente si la solución
concuerda con las condiciones dadas.
8) No se desanime si no puede resolver un problema dado. Se requiere
mucho esfuerzo y práctica para adquirir habilidad para resolver
problemas aplicados. ¡Siga intentando!
Problemas
1) Un químico tiene 10 ml de una solución que contiene 30 % de
concentración de ácido, ¿Cuántos mililitros de ácido puro deben
agregarse para aumentar la concentración a 50%?
2) Un radiador contiene 8 litros de una mezcla de agua y anticongelante. Si
40% de la mezcla es anticongelante, ¿qué cantidad de mezcla debe
eliminarse y reemplazarse por anticongelante puro para que la mezcla
resultante contenga 60% de anticongelante?
3) Dos ciudades, A y B, están conectadas por medio de una carretera de
150 km (kilómetros). Un automóvil sale de A a la 1:00 P.M y viaja a una
velocidad uniforme de 40 km/h hacia B. Treinta minutos más tarde, otro
automóvil sale de A y viaja hacia B a una velocidad uniforme de 55 km/h.
¿A qué hora alcanza el segundo automóvil al primero?
4) Tomás puede hacer cierto trabajo en 3 horas, mientras que Roberto
puede hacer el mismo en 4 horas. Si trabajan juntos, ¿cuánto tiempo les
lleva hacer el trabajo?
5) En la figura se muestra la sección transversal de una casa de dos pisos
para la que la altura central del segundo piso, h, todavía no ha sido
determinada. Encontrar h tal que el área transversal del segundo piso
sea la misma que la del primero.

128. 128
6) Se desea construir un silo grande para grano que contenga la forma de
un cilindro circular con una semiesfera unida a la parte superior. El
diámetro del almacén debe ser de 30 pie, pero la altura no se ha
determinado aún. Encuentre la altura total que debe tener el silo para
que su capacidad sea de 11 250 pie3
.
7) La sección transversal de un canal de desagüe es un trapecio isósceles,
cuya base menor es de 3 pie, y cuya altura, de 1 pie (ver figura).
Determine el ancho que debe tener la base mayor para que el área
transversal del canal sea de 5pie2
.
8) Un granjero desea cercar un terrero rectangular y planea usar 180 pie de
material y parte de la orilla de un río en vez de cercar en un uno de los
lados del rectángulo. Encuentre el área del terreno si la longitud del lado
paralelo a la orilla del río es
a) El doble de la longitud de uno de los lados adyacentes;
b) La mitad de la longitud de un lado adyacente.
c) La misma longitud de un lado adyacente.
9) Un ingeniero consultor cobra 80$ por hora y su ayudante recibe $20 por
hora. Por cierto trabajo, un cliente recibió un a cuenta de $580. Si el
ayudante trabajó 5 horas menos que el ingeniero, ¿cuánto tiempo
trabajó cada uno?
10)Se va a fabricar una caja de base cuadrada y sin tapa, con una hoja
cuadrada de estaño, cortando cuadrados de 3 pulgadas de cada esquina
y doblando los lados. Si la caja debe tener 48 pulgadas cúbicas, ¿qué
tamaño debe tener la hoja que se debe usar?

129. 129
11)El diámetro de un círculo es de 10 cm. ¿Qué cambio en el radio
disminuirá el área en 16 cm2
?
12)La hipotenusa de un triángulo rectángulo mide 5 cm. Halle la medida de
los catetos sabiendo que su suma es 6 cm.
13)Un hombre desea usar 6m3
de concreto para construir el piso de un
patio rectangular. Si la longitud del patio debe ser el doble del ancho y el
grosor del piso debe ser 8 cm, encuentre las dimensiones del patio.
14)Se quiere construir un barril de petróleo cilíndrico y cerrado con una
altura de 4 pie, de manera que el área superficial total sea de 10 pie2
.
Determine el diámetro del barril.
15)Se dese que un acuario de altura 1.5 pie tenga un volumen de 6 pie3
. Si
x representa la longitud de la base, y y la anchura (vease figura).
a) Exprese y como función de x.
b) Exprese como función de x el número total de pies cuadrados de vidrio
que se requieren para la construcción.
Aplicaciones de GeoGebra en la Resolución de Problemas
1. Construir usando lápiz y papel el siguiente rombo:
2) Dado un triángulo ABC, construir un triángulo cuya superficie sea 1/6 de la del
triángulo ABC.
3) Dado un segmento AC y una recta R, encontrar un punto B perteneciente a la recta tal que
el ángulo ABC mida 60°.
4) ¿Qué estrategias puedes utilizar para construir la siguiente figura? (utiliza el soffware
GeoGebra)

130. 130
5. Dado un triángulo ABC, construir un hexágono que tenga la misma superficie que ABC.
6. Dadas dos circunferencias C y C', sin intersección y tal que ninguna es exterior a la otra,
encontrar E y G en C y F en C' tales que la medida del ángulo EFG sea máxima.
Problemas de profundización
7. Dada una circunferencia C y dos puntos A y M sobre C. Se toma un punto B sobre C y se
construye un punto C tal que el segmento AM sea mediana de ABC. Hallar B para que el área
del triángulo ABC sea máxima.
8. Son dados un triángulo ABC, y un punto P. Sea S1 el punto simétrico de P con respecto
a A, S2 el punto simétrico de S1 con respecto a B y S3 el punto simétrico de S2 con respecto
a C. Hallar el lugar geométrico de S3 al mover P.
9. Dado un segmento AB y un punto X sobre AB. Se traza por X la recta r, perpendicular a AB.
Sea O un punto sobre la recta r y C la circunferencia con centro O que pasa por A. Por B se
trazan las tangentes a C, que tocan a C en T1 y T2. Hallar el lugar geométrico de T1 y T2 al
mover O sobre r.
10. Dadas una circunferencia C y una cuerda DA sobre la circunferencia. Se toma otro
punto B sobre C (distinto de A y de D) y se traza la recta s perpendicular por A a DB. La
intersección entre s y la recta DB es C. Hallar B para que el área del triángulo ABC sea
máxima.
11. Dado un triángulo ABC, sea P un punto cualquiera del plano. Se trazan las mediatrices
de AP, BP y CP que se intersectan en tres puntos, A’, B’ y C’. Hallar un punto P para que los
triángulo ABC y A’B’C’ sean semejantes.
12. Sean C1 y C2 dos circunferencias que se intersectan en A y B donde AB es diámetro de C1.
Sea P un punto sobre C2 en el interior de C1. Construir dos puntos C y D sobre C1tales
que CD sea perpendicular a AB y <CPD sea recto, usando sólo Recta por dos Puntos (line by 2
points), Intersección de 2 objetos (intersection) y Recta perpendicular (perpendicular line).
13.
i. Dados tres puntos A, B y C no alineados, encontrar puntos A’, B’ y C’
en BC, AC y AB respectivamente de manera que los triángulos ABC y A’B’C’ tengan el mismo
baricentro.
ii. Dados tres puntos A, B y C no alineados, encontrar puntos A’, B’ y C’
en BC, AC y AB respectivamente de manera que los triángulos ABC y A’B’C’ tengan el mismo
circuncentro.

131. 131
14. Dado un paralelogramo ABCD, encontrar cuatro puntos A’, B’, C’ y D’ todos interiores al
paralelogramo tales que las ternas de puntos A A’ D’, B B’ A’, C C’ B’ y D D’C’ están alineados;
y los polígonos ADD’, DC’C, CB’B, AA’B y A’B’C’D’ tienen áreas iguales.
15. Construir una circunferencia de centro O. Sean AB y SJ dos diámetros perpendiculares, en
el arco menor BS tomar H variable. Para cada H se determinan F, la intersección
entre AH y SB y T la intersección entre SA y BH.
i. Demostrar que TF y AB son ortogonales.
ii. Hallar el lugar geométrico del circuncentro de FSH.
16. Dado un triángulo ABC, encontrar el lugar geométrico de los puntos P interiores al
triángulo tales que d(P, BC) = d(P, AC) + d(P, AB).
Nota: d(P, BC) es la distancia de P a la recta BC.
17. Construir una circunferencia y tomar un punto A fijo sobre ella. Trazar una recta r variable
por A que sea secante a la circunferencia en A y B. Construir un trapecio isósceles ABCD de
bases AB y CD tal que AD = DC = 1/2 AB.
i. Demostrar que la recta BC pasa por un punto fijo.
ii. Hallar el lugar geométrico de C.
iii. Se traza por D una recta t perpendicular a AC. Sea P el punto de intersección entre t y AB.
Se toman J en la semirrecta AB y X en la semirrecta PD tales que AJ = PX. Demostrar que la
mediatriz de JX pasa por el incentro del triángulo APD.
18. Construir un triángulo ABC, y luego encontrar
puntos A’, B’ y C’ en BC, AC y AB respectivamente tales que A’B’ sea perpendicular
a BC, B’C’ sea perpendicular a AC y C’A’ sea perpendicular a AB.
19. Construir la figura dada, en donde ABCD es un cuadrado y AEF es un triángulo equilátero.
20. Sea ABC un triángulo isósceles (AB = AC). Se traza la mediatriz m de AC y la
bisectriz n del ángulo C. Si m, n y AB se cortan en un sólo punto, cuánto mide el ángulo A?
21. Sean A, B y C puntos sobre una circunferencia. Llamemos H al ortocentro del triángulo.
Hallar el lugar geométrico de H al mover A sobre la circunferencia.

132. 132
22. Dados 3 puntos A, B y C, construir el trapecio isósceles ABCD donde AB = CD y BC es
paralelo a AD (BC distinto de AD).
23. Sean A, B y C puntos sobre una circunferencia. Llamemos G al baricentro del triángulo.
Hallar el lugar geométrico de G al mover A sobre la circunferencia.
24. Dado un triángulo ABC, sean D, E y F los puntos medios de los
lados BC, CA y AB respectivamente. Por D se trazan las rectas M1 y M2 perpendiculares
a AB y ACrespectivamente. Por E se trazan las rectas M3 y M4 perpendiculares
a BC y AB respectivamente. Por F se trazan las rectas M5 y M6 perpendiculares
a AC y BCrespectivamente. Sea A´ la intersección entre M4 y M5. Sea B´ la intersección
entre M6 y M1. Sea C´ la intersección entre M2 y M3. Demostrar que los triángulos ABC y A´B´C´
son semejantes y hallar la razón de semejanza.
25. Se tienen dados tres puntos: O, G y M. Construir un triángulo de forma tal que O sea su
circuncentro, G su baricentro, y M el punto medio de un lado.
26. Sea ABC un triángulo y H su ortocentro. Se traza la altura desde A, que corta a BC en D.
Sobre la prolongación de la altura AD se toma el punto E de tal modo que los ángulos <CAD y
<CBE sean iguales. Probar que BE = BH.
27. Sea C una circunferencia, y M un punto variable en su exterior. Por M se trazan las
tangentes a C. Sean A y B los puntos de tangencia. Hallar el lugar geométrico del incentro del
triángulo MAB al variar M.
28. i) Encontrar un punto D en el interior de un triángulo ABC tal que las áreas de los
triángulos ABD, BCD y CAD sean iguales.
ii) Idem con D en el exterior de ABC.
29. Sea ABC un triángulo y M un punto variable sobre AB. N es el punto en la prolongación
de AC tal que CN = BM y que no pertenece a la semirrecta CA. Se construye el
paralelogramo BMNP (en ese orden). Hallar el lugar geométrico de P al variar M.
30. Sea ABCD un cuadrilátero. Sean C1, C2, C3, C4 las circunferencias de
diámetros AB, BC, CD y DA respectivamente. Sean P, Q R y S los puntos de intersección (que
no son vértices de ABCD) de C1 y C2; C2 y C3; C3 y C4; C4 y C1 respectivamente.
Demostrar que los cuadriláteros ABCD y PQRS son semejantes.
31. M, N y P son tres puntos alineados, con N entre M y P. Sea r la mediatriz de NP. Se toma
un punto O sobre r. C es la circunferencia con centro O que pasa por N. Las tangentes por M a
C cortan a C en T y T'.
Hallar el lugar geométrico del baricentro del triángulo MTT' al variar O sobre r.
32. Q y R son los centros de tres circunferencias que pasan por el mismo punto O.
Sean A, B y C los puntos (distintos de O) de interesección de las circunferencias.
Demostrar que A, B y C están alineados si y solo si O, Q y R están en una misma
circunferencia.
33. Construir la siguiente figura donde las tres circunferencias chicas tienen el mismo radio y
una de las circunferencias chicas y la circunferencia grande son concéntricas.

133. 133
34. Se dan una circunferencia C1 de centro O, un punto P en ella. Sea C2 una circunferencia de
diámetro OP. Trazar el cuadrado OABC donde A pertenece a C2 y B pertenece a C1 (pero no a
C2).
35. Se dan una circunferencia de centro O y un punto A exterior a ella. Construir un
rombo ABOC donde B y C son puntos de la circunferencia.
36. Analizar cuándo existe el rombo de la construcción del problema anterior y también cuándo
dicho rombo es un cuadrado.
37. Construir un triángulo isósceles ABC (AB = BC) donde la altura desde A (hA) mide un tercio
de la medida de AB.
38) Sea ABC un triángulo equilátero, se traza una circunferencia cuyo diámetro está incluido
en AB y es tangente a AC y BC. Se traza la recta r que es paralela a AB y tangente a la
circunferencia. Dicha recta interesa a los lados AC y BC en D y E respectivamente. Hallar la
relación entre los perímetros de los triángulos ABC y CDE.
39. Se da un hexágono regular ABCDEF. Sea A’ el simétrico de A con respecto a D, sea C’ el
simétrico de C con respecto a F, sea E’ el simétrico de E con respecto a B. Sea G el punto
medio de DA’, sea H el punto medio de FC’, sea I el punto medio de BE’. Calcular el área del
triángulo GHI sabiendo que el área del hexágono regular es 38.
40. Dado un triángulo isósceles ABC (AB = BC), sean r y s las mediatrices
de AB y BC respectivamente. Sea D el simétrico de A con respecto a s y sea E el simétrico
de Ccon respecto a r. Hallar la medida del ángulo <DBE en función de la medida del ángulo
<ABC.
41. Construir la figura, donde CDEF y C’D’E’F’ son cuadrados.

134. 134
42. Construir un romboide ABCD, (AB = DA, BC = CD), donde los ángulos <B y <D son rectos y
(AC / BD)^2 = 2.
43. Inscribir una circunferencia en un cuarto de circunferencia.
44. Dado un triángulo equilátero ABC se trazan r que pasa por A y es perpendicular
a AB, s que pasa por B y es perpendicular a BC, t que pasa por C y es perpendicular a CA.
Quedándose formado un triángulo equilátero A’B’C’. Calcular la razón entre las áreas de dichos
triángulos.
45. Dado un triángulo ABC, se traza la bisectriz r del ángulo C, luego se construye el
cuadrado ADBE (en el mismo sentido que ABC). Sea P la intersección entre r y BE. Calcular la
relación entre áreas del cuadrado y el triángulo si CP = AD y DB // r.
46. Sea ABCDEFGH un octógono regular, se trazan las rectas AB, CD y GF formándose un
triángulo. Demostrar que la relación entre las áreas y los perímetros del triángulo y el octógono
regular es la misma.
47. Dado un hexágono regular ABCDEF, construir un cuadrado GHIJ,
donde G, H, I, J pertenecen a AB, BC, DE, EF respectivamente.
48. ¿Es único el cuadrado del problema anterior? Justificar.
49. Dado un triángulo ABC construir el rombo BEFG sabiendo que E, F y G son puntos
pertenecientes a cada uno de los lados del triángulo (uno por lado).
50. Dado un cuadrilátero ABCD (en ese orden) , hallar la medida
de BDC si ABD = 45, DBC = 60 ; BAC = 30 , CAD = 60.
51. Dado un triángulo ABC equilátero , sea A
+
el simétrico de A con respecto a B, sea A
-
el
simétrico de A con respecto a C; sea B
+
el simétrico de B con respecto a C, sea B
-
el simétrico
de B con respecto a A y sea C
+
el simétrico de C con respecto a A, sea C- el simétrico de C con
respecto a B. Se trazan las rectas A
+
A
-
, B
+
B
-
y C
+
C
-
formándose el triángulo A’B’C’ en las
intersecciones de dichas rectas. Probar que dichos triángulos son semejantes. Averiguar la
razón de semejanza.( AB / A’B’).