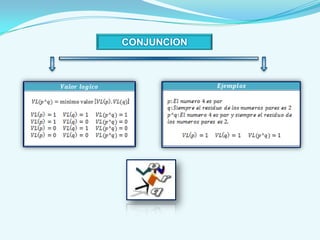
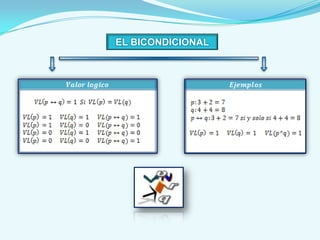
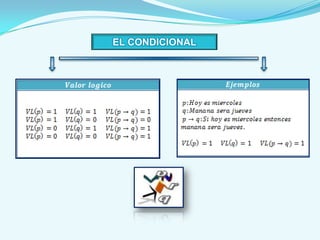
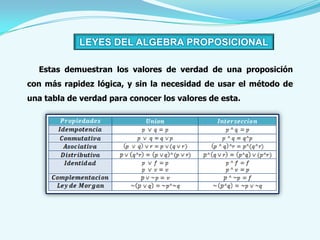
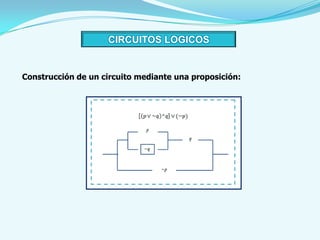
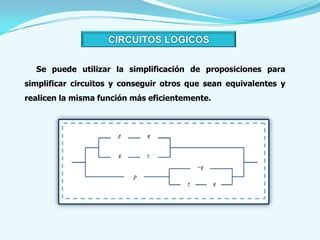
Este documento presenta los conceptos básicos del cálculo proposicional, incluyendo las definiciones de proposición, proposición simple, proposición molecular, operadores lógicos como la negación, conjunción, disyunción inclusiva y exclusiva, condicional y bicondicional. También explica las formas proposicionales, tautologías, contradicciones, leyes del álgebra proposicional, circuitos lógicos y métodos de demostración como la demostración directa y por contrarreciproca.