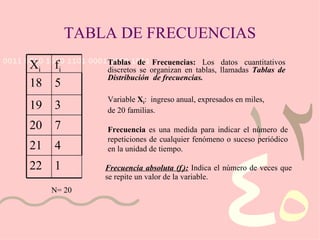
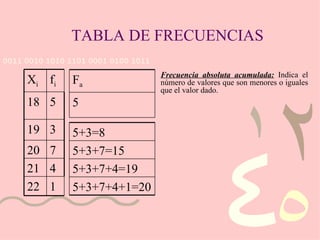
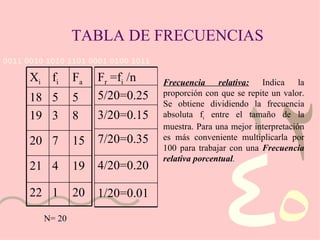
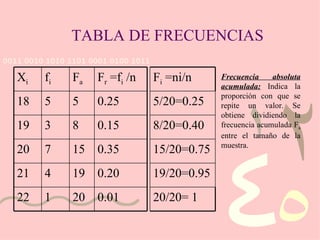
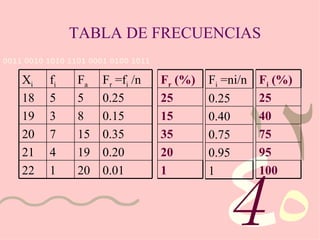
El documento describe el uso de estadística descriptiva para evaluar el estatus socioeconómico de estudiantes y desarrollar programas de ayuda financiera. Presenta datos sobre los ingresos anuales de 20 familias estudiantiles y construye una tabla de frecuencias con las medidas de frecuencia absoluta, relativa y acumulada.

1. ESTADISTICA DESCRIPTIVA ESTRATEGIA DIDACTICA: “ABP”

2. APLICACIÓN DESARROLLADA Evaluar el estatus socio económico de la población estudiantil y determinar necesidades con la finalidad de desarrollar programas de ayuda financiera a los estudiantes de estudios superiores; postgrados y maestrías. PROBLEMA 1

3. ESTADÍSTICA DESCRIPTIVA La estadística descriptiva es una parte de la estadística que se dedica a analizar y representar los datos. Este análisis es muy básico, pero fundamental en todo estudio. Aunque hay tendencia a generalizar a toda la población las primeras conclusiones obtenidas tras un análisis descriptivo, su poder inferencial es mínimo. Algunas de las técnicas empleadas en este primer análisis de los datos se enmarcan en conceptos básicos. Estudio de cálculos en una serie de medidas de tendencia central, para ver en qué medida los datos se agrupan o dispersan en torno a un valor central.

4. ESTADISTICA DESCRIPTIVA La estadística recoge, ordena y analiza datos para estudiar las características o el comportamiento de un colectivo. Variable Estadística es una propiedad o característica de la población que estamos interesados en estudiar Opinión de los Panameños sobre la seguridad social. Número de goles marcados por los equipos de fútbol Infantil. Importancia de las próximas elecciones para Presidente de la República. 1.1 Seguridad social. 2.1 Goles marcados. 3.1 Presidente de la República. 2

5. TABLA DE FRECUENCIAS Evaluar estatus socio económico de la población estudiantil. Desarrollar programas de ayuda financiera a los estudiantes de estudios superiores. Consideraciones: Información presentada menor de treintas datos. No se toma en consideración el método de muestreo. caso para datos no agrupados. PROBLEMA:

6. PLANTEAMIENTO * Muestra de 20 Estudiantes, siendo n = 20 * Variable X : ingreso anual, expresados en miles. * Valores observados: 18, 20, 22, 19, 18, 20, 18, 19, 21, 20 20, 21, 18, 20, 21, 19, 20, 21, 18, 20

7. TABLA DE FRECUENCIAS Valores observados: 18, 20, 22, 19, 18, 20, 18, 19, 21, 20 20, 21, 18, 20, 21, 19, 20, 21, 18, 20 18, 18, 18, 18, 18 5 19, 19, 19, 3

8. Organización de datos Cuantitativos Discretos Tablas de Frecuencias: Los datos cuantitativos discretos se organizan en tablas, llamadas Tablas de Distribución de frecuencias. tipos de frecuencias: Frecuencia absoluta: Indica el número de veces que se repite un valor de la variable. Frecuencia relativa: Indica la proporción con que se repite un valor. Se obtiene dividiendo la frecuencia absoluta entre el tamaño de la muestra. Para una mejor interpretación es más conveniente mutiplicarla por 100 para trabajar con una Frecuencia relativa porcentual . Frecuencia absoluta acumulada: Indica el número de valores que son menores o iguales que el valor dado. Frecuencia relativa porcentual acumulada: Indica el porcentaje de datos que son menores o iguales que el valor dado. 3

9. Variable X i : ingreso anual, expresados en miles, de 20 familias. Tablas de Frecuencias: Los datos cuantitativos discretos se organizan en tablas, llamadas Tablas de Distribución de frecuencias. Frecuencia es una medida para indicar el número de repeticiones de cualquier fenómeno o suceso periódico en la unidad de tiempo. TABLA DE FRECUENCIAS Frecuencia absoluta (f i ): Indica el número de veces que se repite un valor de la variable. N= 20 X i f i 18 5 19 3 20 7 21 4 22 1

10. TABLA DE FRECUENCIAS Frecuencia absoluta acumulada: Indica el número de valores que son menores o iguales que el valor dado. X i f i 18 5 19 3 20 7 21 4 22 1 5+3=8 5+3+7=15 5+3+7+4=19 5+3+7+4+1=20 F a 5

11. TABLA DE FRECUENCIAS Frecuencia relativa: Indica la proporción con que se repite un valor. Se obtiene dividiendo la frecuencia absoluta f i entre el tamaño de la muestra. Para una mejor interpretación es más conveniente multiplicarla por 100 para trabajar con una Frecuencia relativa porcentual . N= 20 X i f i F a 18 5 5 19 3 8 20 7 15 21 4 19 22 1 20 F r =f i /n 5/20=0.25 3/20=0.15 7/20=0.35 4/20=0.20 1/20=0.01

12. Frecuencia absoluta acumulada: Indica la proporción con que se repite un valor. Se obtiene dividiendo la frecuencia acumulada F a entre el tamaño de la muestra. TABLA DE FRECUENCIAS X i f i F a F r =f i /n 18 5 5 0.25 19 3 8 0.15 20 7 15 0.35 21 4 19 0.20 22 1 20 0.01 F i =ni/n 5/20=0.25 8/20=0.40 15/20=0.75 19/20=0.95 20/20= 1

13. TABLA DE FRECUENCIAS 4 X i f i F a F r =f i /n 18 5 5 0.25 19 3 8 0.15 20 7 15 0.35 21 4 19 0.20 22 1 20 0.01 F i =ni/n 0.25 0.40 0.75 0.95 1 F r (%) 25 15 35 20 1 F i (%) 25 40 75 95 100

14. GRACIAS…