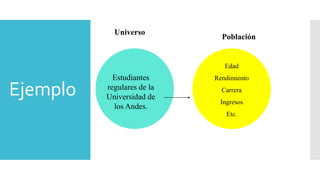
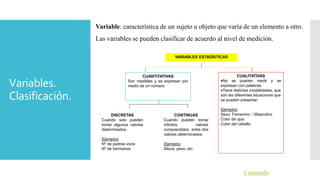
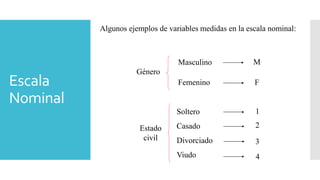
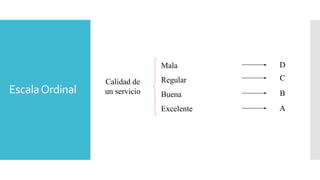
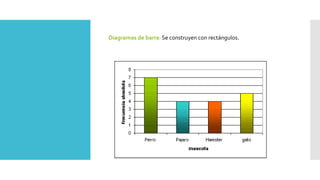
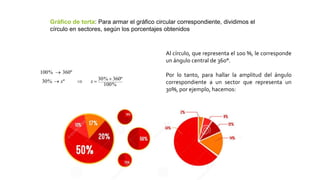
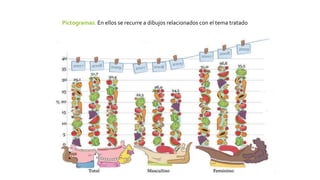
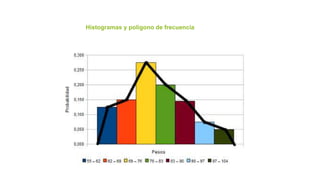
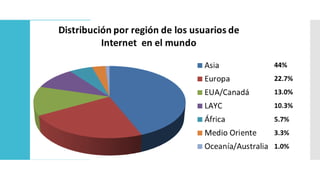
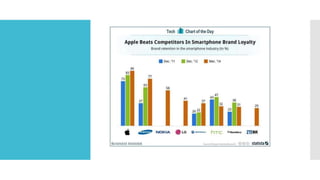
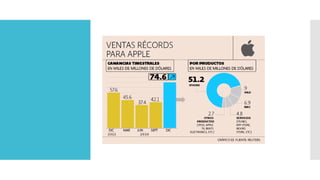
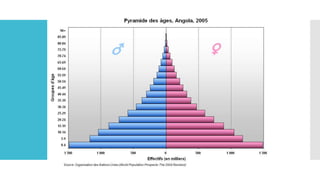
Este documento introduce los conceptos básicos de probabilidad y estadística. Explica que la probabilidad proporciona una base para evaluar la fiabilidad de las conclusiones estadísticas. Define términos como población, muestra, parámetro y variable. Describe las diferentes escalas de medición para variables cualitativas y cuantitativas. Finalmente, resalta que los gráficos estadísticos como diagramas de barras y tortas son útiles para comunicar la información de manera clara.

1. Probabilidad y Estadística

2. Introducción
 En la vida cotidiana aparecen muchas situaciones en las que los
resultados observados son diferentes aunque las condiciones
iniciales en las que se produce la experiencia sean las mismas.
 la probabilidad pretende ser una herramienta para modelizar y
tratar con situaciones de este tipo; por otra parte, cuando
aplicamos las técnicas estadísticas a la recogida, análisis e
interpretación de los datos, la teoría de la probabilidad
proporciona una base para evaluar la fiabilidad de las conclusiones
alcanzadas y las inferencias realizadas.
 Debido al importante papel desempeñado por
la probabilidad dentro de la estadística, es necesario familiarizarse
con sus elementos básicos, lo que constituye el objetivo del
presente tema.

3. CONCEPTOS
BÁSICOS

4. Definición de
Estadística
Conjunto de teorías y métodos que han sido desarrollados
para tratar la recopilación, organización y análisis de datos o
hechos numéricos, con el fin de sacar conclusiones.

5. Clasificación
de la
Estadística
Según el tipo
de
investigación
Estadística Descriptiva.
Tiene por objetivo fundamental la
descripción numérica de un conjunto de
datos. No generaliza las conclusiones
obtenidas a otros grupos de datos.
Estadística Inferencial.
Usa la información aportada por una muestra
para sacar conclusiones de la población de la
cual ha sido extraida; siempre recordando
que existe la probabilidad de hacerlo en
forma errada

6. Población,
universo y
muestra
Universo: se define como el conjunto de sujetos o elementos
que tienen una característica común, observable y susceptible de
ser medida.
Población: conjunto de todas las mediciones u observaciones
hechas sobre una o varias de las características de los
elementos del universo.
Muestra: subconjunto de elementos del universo o la
población.

7. Ejemplo
Estudiantes
regulares de la
Universidad de
los Andes.
Universo
Edad
Rendimiento
Carrera
Ingresos
Etc.
Población

8. Parámetro: valor numérico que describe una característica de la población. Los
parámetros se estiman a partir de la información aportada por una muestra de la
población.
Ejemplo: Si se considera como universo a todos los estudiantes regulares de la Universidad de Los
Andes, la edad promedio de estos, el porcentaje de estudiantes de sexo femenino que fuman, el
ingreso medio todos los estudiantes, son valores que describen a este conjunto.

9. Frecuencia absoluta: es el número de veces que se repite una observación o
valor de la variable (f).
Frecuencia relative: de una observación: es el cociente entre su frecuencia
absoluta y el número total de observaciones realizadas (fr).
n
f
rf 

10. Variables.
Clasificación.
Variable: característica de un sujeto u objeto que varía de un elemento a otro.
Las variables se pueden clasificar de acuerdo al nivel de medición.
Contenido
VARIABLES ESTADÍSTICAS
CUANTITATIVAS
Son medibles y se expresan por
medio de un número
CUALITATIVAS
No se pueden medir y se
expresan con palabras.
Tiene distintas modalidades, que
son las diferentes situaciones que
se pueden presentar.
Ejemplos:
Sexo: Femenino – Masculino
Color de ojos
Color del cabello
DISCRETAS
Cuando solo pueden
tomar algunos valores
determinados.
Ejemplos:
Nº de padres vivos
Nº de hermanos
CONTINUAS
Cuando pueden tomar
infinitos valores
comprendidos entre dos
valores determinados.
Ejemplos:
Altura, peso, etc

11. Escalasde medición

12. Escalas Escalas
de
medición
Escala Nominal
Escala Ordinal
Escala de Intervalo
Escala de Razón

13. Escala
Nominal
1. Se clasifica a los sujetos en categorías, mutuamente
excluyentes y totalmente exhaustivas, tal que todos los
sujetos clasificados en la misma categoría son equivalentes
respecto a la variable que se está midiendo.
2. Sólo tiene sentido la relación de igualdad-desigualdad.
3. Se pueden usar números, letras o símbolos para identificar a
cada categoría de la variable.
4. No se puede realizar ninguna operación aritmética en esta
escala.

14. Escala
Nominal
Algunos ejemplos de variables medidas en la escala nominal:
Género
Masculino
Femenino
M
F
Estado
civil
Soltero
Casado
Divorciado
Viudo
1
3
2
4

15. EscalaOrdinal
1. Se usa cuando es posible establecer una relación de orden
entre las distintas categorías de la variable. Es decir, prevalece
la relación de orden “mayor que” (>).
2. Se pueden usar letras o números para identificar a cada
categoría de la variable. Los números o letras usados deben
reflejar el orden de las categorías.
3. No se pueden realizar operaciones aritméticas entre los
números asignados a las distintas categorías. Tales números
solo reflejan una relación de orden.

16. EscalaOrdinal
Calidad de
un servicio
Mala
Regular
Buena
Excelente
D
C
B
A

17. Escala de
Intervalo.
1. Posee una unidad de medida constante y arbitraria.
2. Posee un cero “arbitrario”, es decir, no indica la ausencia de la
característica que se está midiendo.
3. Prevalece la relación de orden “mayor que” (>).
4. Entre los valores de la variable solo es posible realizar la suma
y la resta como operaciones aritméticas.

18. Escala de
Intervalo
Tres ejemplos de variables medidas en una escala de intervalo:
1. La temperatura de una ciudad medida en grados Fahrenheit o
Celsius.
2. La altura de las ciudades usando como referencia el nivel del
mar.
3. El rendimiento académico medido en una escala del 0 al 20.
Para cada variable mencionada el cero es “arbitrario”.

19. Escala de
Razón.
1. Posee una unidad de medida constante y arbitraria.
2. Posee un cero “absoluto”, es decir, este valor indica la
ausencia de la característica que se está midiendo.
3. Prevalece la relación de orden “mayor que” (>).
4. Se pueden realizar todas las operaciones aritméticas entre los
valores de la variable.

20. Escala de
Razón
Algunas variables medidas en la escala de razón:
1. Edad.
2. Peso.
3. Estatura.
4. Tiempo invertido por un estudiante en realizar una tarea.
5. Ingreso familiar.

21. Un error en estadística es la diferencia entre el valor de un estimador y el del parámetro
correspondiente. Existen varias causas para producir estos errores. Según la causa son
clasificados en errores de muestreo y de no muestreo.
El error de no muestreo puede ocurrir en cualquier ENCUESTA, sea un censo o una muestra.
Estos errores comprenden errores sistemáticos y equivocaciones.
Los factores que causan error sistemático son: falta de definición clara de la población,
inadecuada elaboración del marco de muestreo, falta de definición del cuestionario, vaga
concepción de la información deseada, métodos imprecisos de entrevistas.
Los errores de muestreo son resultado de la elección casual de unidades de muestreo. Este tipo
de error ocurre porque solo se observa una parte de la población; así que si se hace un censo,
puede esperarse que desaparezca el error de muestreo.
Errores de medición

22. Las cifras significativas están determinadas por el error.

23. Gráficos

24. Gráficos
Estadísticos
Los gráficos estadísticos se utilizan muchísimo, y con
ellos la información obtenida puede ser leída con
claridad y rapidez. Los gráficos más usados son:
diagramas de barras, gráficos circulares, pictogramas,
histogramas, polígono de frecuencia.
Para variables discretas: Para variables continuas:
- diagramas de barras - histogramas
- pictogramas - polígono de frecuencia
- gráfico de torta - gráfico de torta

25. Diagramas de barra: Se construyen con rectángulos.

26. Gráfico de torta: Para armar el gráfico circular correspondiente, dividimos el
círculo en sectores, según los porcentajes obtenidos
Al círculo, que representa el 100 %, le corresponde
un ángulo central de 360°.
Por lo tanto, para hallar la amplitud del ángulo
correspondiente a un sector que representa un
30%, por ejemplo, hacemos:
%100
º360%30º%30
º360%100


xx

27. Pictogramas: En ellos se recurre a dibujos relacionados con el tema tratado

28. Histogramas y polígono de frecuencia

29. Aplicaciones

34. Conclusión
Con todo lo aprendido, podemos concluir que la estadística es una rama
de la matemática que está no se encuentra muy visible en lo cotidiano
pero que en realidad es de mucha utilidad para interpretar y ver desde un
punto de vista muy general datos que se obtienen. A través de sus
gráficas, medidas de tendencia central y de dispersión podemos ver mas
claro y concreto un conjunto de datos que se nos hacen muy
complicados, en resumen son un verdadero método de ayuda para
informar.

35. Bibliografía
http://www.virtual.unal.edu.co/cursos/sedes/manizales/40300
06/lecciones/capituloseis/6_2.html
http://depa.fquim.unam.mx/amyd/archivero/Cifras_significativ
as_15479.pdf
http://thales.cica.es/rd/Recursos/rd97/UnidadesDidacticas/53-
1-u-indice.html
http://www.cortland.edu/FLTEACH/STATS/stat-sp.html
http://ciberconta.unizar.es/docencia/estadistica/