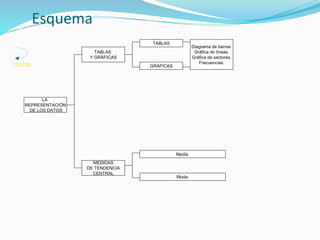
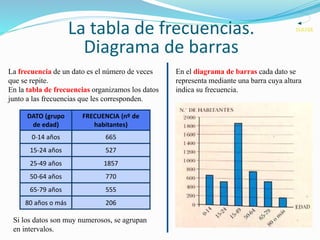
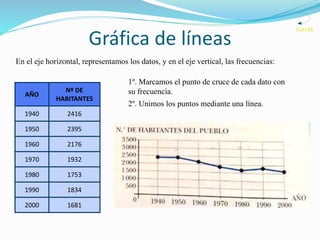
El documento habla sobre diferentes métodos para representar datos, incluyendo tablas de frecuencias, diagramas de barras, gráficas de líneas, gráficos de sectores, y medidas de tendencia central como la media y la moda. Explica cómo construir y leer estos diferentes tipos de representaciones gráficas de datos.

1. Tema 15: La representación
de los datos
Esther Sarasán Peinado
5º de Primaria
2014/15

2. ÍNDICE
 Esquema
 La tabla de frecuencias. Diagrama de barras
 Recuerda
 Gráfica de líneas
 Aprende
 Gráfico de sectores
 Aprende
 La medida y la moda
 Aprende

3. LA
REPRESENTACIÓN
DE LOS DATOS
MEDIDAS
DE TENDENCIA
CENTRAL
TABLAS
Y GRÁFICAS
TABLAS
GRÁFICAS
Diagrama de barras.
Gráfica de líneas.
Gráfica de sectores.
Frecuencias.
Media.
Moda.
Esquema
VOLVER

4. La tabla de frecuencias.
Diagrama de barras
VOLVER
La frecuencia de un dato es el número de veces
que se repite.
En la tabla de frecuencias organizamos los datos
junto a las frecuencias que les corresponden.
Si los datos son muy numerosos, se agrupan
en intervalos.
En el diagrama de barras cada dato se
representa mediante una barra cuya altura
indica su frecuencia.
DATO (grupo
de edad)
FRECUENCIA (nº de
habitantes)
0-14 años 665
15-24 años 527
25-49 años 1857
50-64 años 770
65-79 años 555
80 años o más 206

5. Recuerda
Para recoger los datos y hacer el recuento
de manera más fácil, puedes anotarlos
agrupándolos de 5 en 5, así:
VOLVER

6. Gráfica de líneas
VOLVER
En el eje horizontal, representamos los datos, y en el eje vertical, las frecuencias:
1º. Marcamos el punto de cruce de cada dato con
su frecuencia.
2º. Unimos los puntos mediante una línea.
AÑO
Nº DE
HABITANTES
1940 2416
1950 2395
1960 2176
1970 1932
1980 1753
1990 1834
2000 1681

7. Aprende
Si queremos comparar datos diferentes relativos
al mismo fenómeno, los representamos en una
gráfica doble.
La gráfica nos permite compara ambas
informaciones de “un vistazo”.
VOLVER

8. Gráfico de sectores
VOLVER
Observa que el círculo se ha dividido en
30 partes iguales, que es la suma total de
las frecuencias.
Cuando representamos las frecuencias sobre un círculo, obtenemos un gráfico de
sectores.
Para construirlo, dividimos el círculo en tantas partes iguales como indique la suma
total de las frecuencias y asignamos un sector circular a cada dato según su
frecuencia.
DEPORTE FRECUENCIA
Baloncesto 15
Balonmano 3
Ciclismo 2
Fútbol 6
Tenis 4
TOTAL 30

9. Aprende
Para construir el gráfico, dividimos el círculo en
20 partes iguales o sectores, cada uno de los
cuales medirá:
360º : 20 = 18º
VOLVER

10. La media y la moda
VOLVER
La media y la moda nos dan, en un solo dato, información relativa al conjunto de
todos los datos.
Observa cómo se calculan:
LA MEDIA
Para hallar la media de un conjunto de datos,
obtenemos la suma de todos ellos y dividimos
entre el número de datos:
La temperatura media es de 15ºC.
LA MODA
La moda de un conjuntos de datos es el valor
que más se repite o, lo que es lo mismo, el que
tiene mayor frecuencia.
La moda es de 16ºC.
DÍA LUNES MARTES MIÉRCOLES JUEVES VIERNES SÁBADO DOMINGO
TEMPERATURA
(ºC)
13 16 16 18 16 11 15
TEMPERATURA
(ºC)
11 13 15 16 18
FRECUENCIA 1 1 1 3 1
15
7
15111618161613


Media

11. Aprende
A la media se la denomina también media
aritmética o promedio. Se calcula solo cuando
los datos son numéricos.
VOLVER