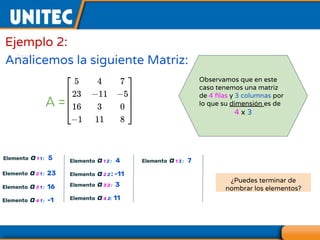
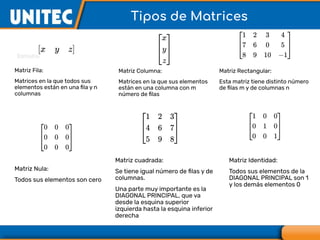
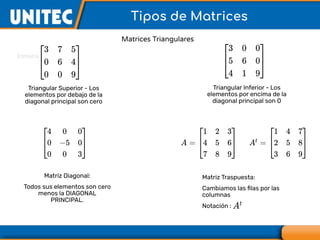
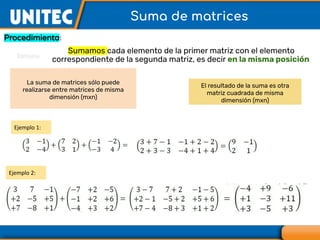
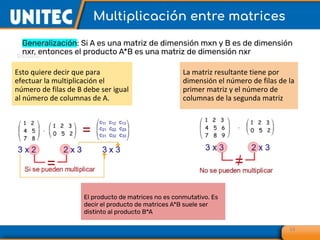
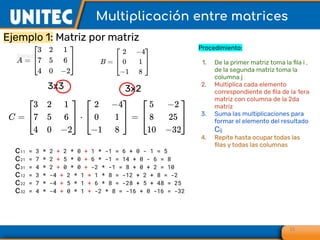
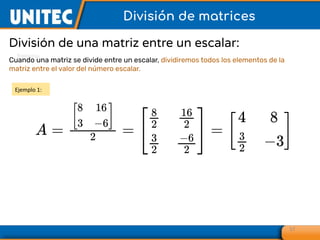
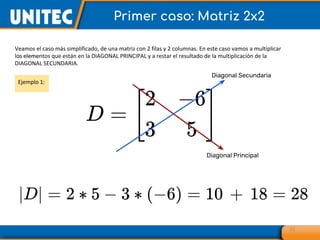
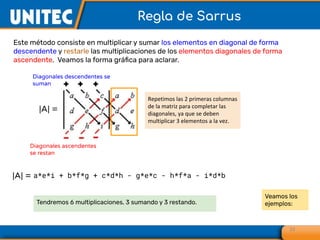
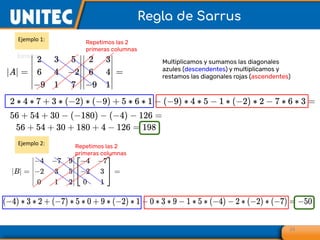
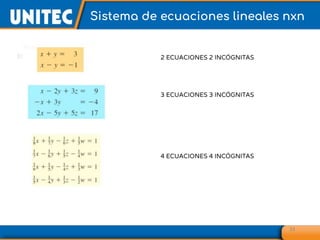
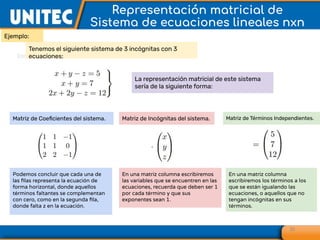
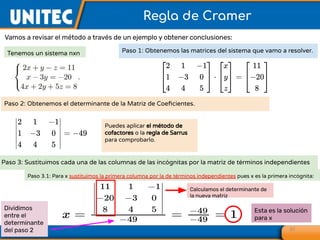
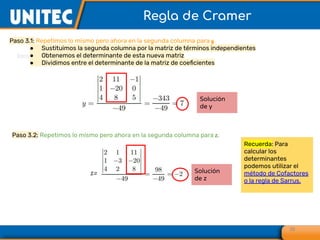
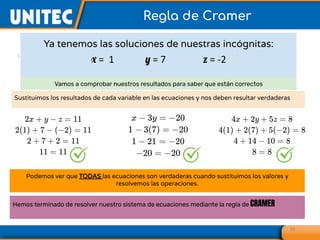
El documento aborda el tema de matrices en álgebra lineal, definiendo tipos de matrices y sus dimensiones, y destacando su aplicación en diversos campos, como la robótica y la inteligencia artificial. También se explican operaciones con matrices, incluyendo suma, resta, multiplicación y determinación de determinantes, así como su uso en sistemas de ecuaciones lineales y la regla de Cramer para su solución. Se incluye una variedad de ejemplos y descripciones de métodos para calcular determinantes y resolver sistemas matriciales.

1. TEMA 1. MATRICES
Ing. Hugo García Flores
UNITEC. Álgebra Lineal Aplicada

2. 1.1 DEFINICIÓN
Y TIPOS DE MATRICES

3. Definamos Matriz:
Una matriz es un conjunto de números o expresiones que aparecen ordenados
en filas (n) y columnas (m).
Cada expresión o número dentro de la
matriz es un elemento, representado
por aij, donde el subíndice i indica la
fila y el subíndice j indica la columna
en que se encuentra.
Columna m
Fila n
El número de elementos de la matriz se puede obtener de la operación mxn,
esto también se le conoce como dimensión de la matriz.
Se usan mayúsculas para
nombrar a las matrices

4. Definamos Matriz
Ejemplo 1:
Analicemos la siguiente Matriz:
A =
Esta Matriz tiene 3 filas y 3 columnas por
lo tanto tiene una dimensión 3 x 3
Columna 1 Columna 2 Columna 3
Fila 1
Fila 1
Fila 1
Elemento fila 1 columna 1 a1 1 : 1 Elemento fila 1 columna 2 a1 2 : 5 Elemento fila 1 columna 3 a3 1 : -4
Elemento fila 2 columna 1 a2 1 : 7 Elemento fila 2 columna 2 a2 2 : 10 Elemento fila 2 columna 3 a2 3 : 9
¿Puedes terminar de nombrar los elementos?

5. Ejemplo 2:
Analicemos la siguiente Matriz:
A =
Observamos que en este
caso tenemos una matriz
de 4 filas y 3 columnas por
lo que su dimensión es de
4 x 3
Elemento a1 1 : 5
Elemento a2 1 : 23
Elemento a3 1 : 16
Elemento a4 1 : -1
Elemento a1 2 : 4
Elemento a2 2 : -11
Elemento a3 2 : 3
Elemento a4 2: 11
Elemento a1 3 : 7
¿Puedes terminar de
nombrar los elementos?

6. Usos de las matrices
Las aplicaciones de las matrices son muy diversas, que van desde televisores
hasta física cuántica.
Las imágenes son una matriz de
píxeles
Robotica - Edinsoncs - Ockangplc-automatas
cinematica(automatizacion y robotica)
En robótica representan los
movimientos de los eslabones
How a Television Works, by Sarah.Stitt Last
Las matrices de Pauli miden el
spin de una subpartícula
Lecture 15 4 PAULI SPIN MATRICES, Mareco
Los sistemas de inteligencia
artificial utilizan matrices para
sus predicciones
My Python Pandas Cheat Sheet, Chris I.

7. Tipos de Matrices
Matriz Fila:
Matrices en la que todos sus
elementos están en una fila y n
columnas
Matriz Columna:
Matrices en la que sus elementos
están en una columna con m
número de filas
Matriz Rectangular:
Esta matriz tiene distinto número
de filas m y de columnas n
Matriz Nula:
Todos sus elementos son cero
Matriz cuadrada:
Se tiene igual número de filas y de
columnas.
Una parte muy importante es la
DIAGONAL PRINCIPAL, que va
desde la esquina superior
izquierda hasta la esquina inferior
derecha
Matriz Identidad:
Todos sus elementos de la
DIAGONAL PRINCIPAL son 1
y los demás elementos 0

8. Matrices Triangulares
Triangular Superior - Los
elementos por debajo de la
diagonal principal son cero
Triangular Inferior - Los
elementos por encima de la
diagonal principal son 0
Tipos de Matrices
Matriz Diagonal:
Todos sus elementos son cero
menos la DIAGONAL
PRINCIPAL.
Matriz Traspuesta:
Cambiamos las filas por las
columnas
Notación :

9. 1.2 OPERACIONES
CON MATRICES

10. Suma de matrices
Procedimiento:
Sumamos cada elemento de la primer matriz con el elemento
correspondiente de la segunda matriz, es decir en la misma posición
La suma de matrices sólo puede
realizarse entre matrices de misma
dimensión (mxn)
El resultado de la suma es otra
matriz cuadrada de misma
dimensión (mxn)
Ejemplo 1:
Ejemplo 2:

11. Resta o sustracción de matrices
Procedimiento:
Podemos decir que la resta de dos matrices es la suma de
A con la matriz opuesta de B, ya que vamos a aplicar un signo
negativo a cada elemento de la matriz B, y lo restamos de
cada elemento correspondiente de la matriz A.
Como en la suma de matrices ,sólo
pueden restarse matrices de la
misma dimensión (mxn)
Ejemplo 1:
Ejemplo 2:
Ejemplo 3:

12. Multiplicación de matrices
Existen diferentes casos en la multiplicación
de matrices que vale la pena verlos por
separado.
Continua para descubrirlos:

13. Multiplicación de una matriz por un escalar
Procedimiento:
Al multiplicar los elementos de una matriz A por un número real (k) cualquiera
obtendremos el resultado como una matriz de dimensión igual a la de A.
Ejemplo 1:
Ejemplo 2:

14. Multiplicación entre matrices
14
Generalización: Si A es una matriz de dimensión mxn y B es de dimensión
nxr, entonces el producto A*B es una matriz de dimensión nxr
Esto quiere decir que para
efectuar la multiplicación el
número de filas de B debe ser igual
al número de columnas de A.
La matriz resultante tiene por
dimensión el número de filas de la
primer matriz y el número de
columnas de la segunda matriz
El producto de matrices no es conmutativo. Es
decir el producto de matrices A*B suele ser
distinto al producto B*A

15. Ejemplo 1: Matriz por matriz
15
Multiplicación entre matrices
3x3 3x2
Procedimiento:
1. De la primer matriz toma la fila i ,
de la segunda matriz toma la
columna j
2. Multiplica cada elemento
correspondiente de fila de la 1era
matriz con columna de la 2da
matriz
3. Suma las multiplicaciones para
formar el elemento del resultado
Cij
4. Repite hasta ocupar todas las
filas y todas las columnas
c11 = 3 * 2 + 2 * 0 + 1 * -1 = 6 + 0 - 1 = 5
c21 = 7 * 2 + 5 * 0 + 6 * -1 = 14 + 0 - 6 = 8
c31 = 4 * 2 + 0 * 0 + -2 * -1 = 8 + 0 + 2 = 10
c12 = 3 * -4 + 2 * 1 + 1 * 8 = -12 + 2 + 8 = -2
c22 = 7 * -4 + 5 * 1 + 6 * 8 = -28 + 5 + 48 = 25
c32 = 4 * -4 + 0 * 1 + -2 * 8 = -16 + 0 -16 = -32

16. Matriz fila por matriz columna
16
Multiplicación de matrices
Es posible solo cuando el número de columnas de la matriz fila es
igual al número de filas de la matriz columna
Ejemplo 1:
Ejemplo 2:
Esta operación NO se puede realizar ya que el
número de filas de la Matriz G es mayor al número
de columnas de la matriz F

17. División de matrices
División de una matriz entre un escalar:
17
Cuando una matriz se divide entre un escalar, dividiremos todos los elementos de la
matriz entre el valor del número escalar.
Ejemplo 1:

18. 18
1.3 DETERMINANTES

19. Determinantes
La definiciòn de determinantes es abstracta. Vamos a verla desde un punto de
vista gráfico.
Empecemos con una matriz base en el origen:
19
Piensa
en esta
área de
1x1,
vamos a
estudiar
que es
lo que le
pasa
Si modificamos la matriz, vamos a
modificar el espacio, podemos
verlo con este ejemplo
El área se ha inclinado y tenemos
ahora este paralelogramo, las
determinantes de la matriz es
cuanto mide el área de esa
transformación
Claro no todo se puede
ver en una diapositiva,
te recomiendo ver el
video del link para
entender que es una
determinante:
https://www.youtube.c
om/watch?v=yt3eoYvG
el0

20. Vamos revisar directamente el procedimiento de
como obtener la determinante de una matriz,
recordemos que es el área de la transformación
que ha sufrido el espacio. Piensa cuando escalas
una imagen y la deformas, estás aplicando
determinantes.
20
Cálculo de Determinantes

21. 21
Primer caso: Matriz 2x2
Veamos el caso más simplificado, de una matriz con 2 filas y 2 columnas. En este caso vamos a multiplicar
los elementos que están en la DIAGONAL PRINCIPAL y a restar el resultado de la multiplicación de la
DIAGONAL SECUNDARIA.
Ejemplo 1:
Diagonal Principal
Diagonal Secundaria

22. Para calcular el determinante de una matriz 3x3
principalmente se utilizan 2 técnicas:
● Regla de Sarrus
● Método de Cofactores
22
Segundo caso: Matriz 3x3
Vamos a explorar
cada una de estas
técnicas de
cálculo.

23. Regla de Sarrus
23
Este método consiste en multiplicar y sumar los elementos en diagonal de forma
descendente y restarle las multiplicaciones de los elementos diagonales de forma
ascendente. Veamos la forma gráfica para aclarar.
Repetimos las 2 primeras columnas
de la matriz para completar las
diagonales, ya que se deben
multiplicar 3 elementos a la vez.
Diagonales descendentes se
suman
Diagonales ascendentes
se restan
|A| =
|A| = a*e*i + b*f*g + c*d*h - g*e*c - h*f*a - i*d*b
Tendremos 6 multiplicaciones, 3 sumando y 3 restando.
Veamos los
ejemplos:

24. 24
Regla de Sarrus
Ejemplo 1: Repetimos las 2
primeras columnas
Multiplicamos y sumamos las diagonales
azules (descendentes) y multiplicamos y
restamos las diagonales rojas (ascendentes)
Ejemplo 2: Repetimos las 2
primeras columnas

25. Para aplicar este método primero debemos tomar en cuenta lo que se conoce
como cofactor o menor.
El menor se obtiene de la matriz restante cuando eliminamos una fila y una
columna seleccionada. Esto será útil después para encontrar el determinante.
La forma general de la solución:
25
Método de Cofactores
Revisemos algunos ejemplos para que quede más claro:

26. 26
Método de Cofactores
Ejemplo 1:
Tenemos la matriz:
Calculemos los cofactores C 11, C 32, C 13 ,C 23:
El primer cofactor se encuentra en la fila 1, columna 1, así que la matriz menor son los
elementos restantes. Para obtener su signo elevamos (-1) a la suma de i+j
Soluciones de los ejercicios restantes:

27. El método de cofactores también llamado el teorema de Laplace nos permite encontrar el
determinante de las matrices. Basta seguir los siguientes pasos:
27
Método de Cofactores
● Seleccionamos cualquier fila o columna.
● “Eliminamos” de la matriz original la fila o columna seleccionados.
● Obtenemos el determinante de la matriz ”restante”.
● Multiplicamos cada elemento de la fila o columna escogida
● Se suman los productos obtenidos en el paso 4 y el resultado obtenido es el
determinante.
Tenemos la matriz A
Seleccionamos la primer fila y vamos
a recorrer sus elementos. A eso le
llamaremos los menores
Primer menor: Ocultamos la primer fila y la primer columna. Calculamos el determinante y lo multiplicamos
por el primer elemento
Ejemplo 1:

28. 28
Continuación ejemplo 1:
Continuamos con el elemento 2 de la primer fila, ahora ocultamos la primer fila y la segunda
columna, encontramos su determinante y lo multiplicamos por el elemento
=
Finalizamos con el elemento 3 de la primer fila, ahora ocultamos la primer fila y la tercer columna,
encontramos su determinante y lo multiplicamos por el elemento
=
La operación completa tiene la siguiente forma:
Importante: nota que el orden de los signos de la
operación es + - + (Suma, resta, suma)
Método de Cofactores

29. 29
Ejemplo 2: Evalúe el determinante de la siguiente matriz:
Podemos ver resumido el método antes presentado, tomamos la primer fila, y obtenemos los
determinantes de las matrices menores. Después esos menores los multiplicamos por cada uno
de los elementos de la fila seleccionada
Nuestro resultado es la multiplicación del 1er elemento por el
determinante del menor, ya que las otras multiplicaciones fueron
por cero
Método de Cofactores

30. 30
Ejemplo 3:
Método de Cofactores
No siempre debemos utilizar la primer fila, podemos utilizar cualquiera, se recomienda
utilizar aquella que tenga mayor número de ceros en sus elementos, ya que así se
reduce el número de operaciones.
En este caso
utilizamos la
segunda fila
ya que
contiene el 0
Nota el orden de los signos por la
regla descrita al inicio del método.

31. 31
1.4 Sistema de Ecuaciones Lineales

32. Un sistema de ecuaciones lineales es un conjunto de dos o más
ecuaciones que son polinomios de primer grado, es decir, en sus
términos tienen solo una incógnita (variable) y todos los exponentes de
estas variables es 1.
Se le conoce como sistema nxn cuando tenemos el mismo número de
ecuaciones que de incógnitas.
Gráficamente cada ecuación es una recta.
32
Sistema de ecuaciones lineales nxn

33. 33
Sistema de ecuaciones lineales nxn
2 ECUACIONES 2 INCÓGNITAS
3 ECUACIONES 3 INCÓGNITAS
4 ECUACIONES 4 INCÓGNITAS

34. 34
Representación matricial de
Sistema de ecuaciones lineales nxn
De forma general un sistema de ecuaciones lo
podemos ver así, donde hay términos con una
incógnita que se suman o restan.
La representación matricial del sistema de ecuaciones se escribe de la siguiente forma:
Matriz de coeficientes
Matriz de incógnitas
Matriz de términos
independientes

35. 35
Representación matricial de
Sistema de ecuaciones lineales nxn
Tenemos el siguiente sistema de 3 incógnitas con 3
ecuaciones:
La representación matricial de este sistema
sería de la siguiente forma:
Matriz de Coeficientes del sistema.
Podemos concluir que cada una de
las filas representa la ecuación de
forma horizontal, donde aquellos
términos faltantes se complementan
con cero, como en la segunda fila,
donde falta z en la ecuación.
Matriz de Incógnitas del sistema.
En una matriz columna escribiremos
las variables que se encuentren en las
ecuaciones, recuerda que deben ser 1
por cada término y que sus
exponentes sean 1.
Matriz de Términos Independientes.
En una matriz columna
escribiremos los términos a los
que se están igualando las
ecuaciones, o aquellos que no
tengan incógnitas en sus
términos.
Ejemplo:

36. 36
Solución de un Sistema de
ecuaciones lineales nxn
Encontrar la solución de un sistema de ecuaciones quiere decir que vamos a
encontrar los valores de las incógnitas que hagan verdadero el resultado igualado.
En este caso vamos a explorar un método que aplica para cualquier número de
ecuaciones en tu sistema, recuerda siempre y cuando sea el mismo número de
incógnitas. El método se llama:
REGLA DE CRAMER

37. 37
Regla de Cramer
Vamos a revisar el método a través de un ejemplo y obtener conclusiones:
Paso 1: Obtenemos las matrices del sistema que vamo a resolver.
Paso 2: Obtenemos el determinante de la Matriz de Coeficientes.
Tenemos un sistema nxn
Puedes aplicar el método de
cofactores o la regla de Sarrus
para comprobarlo.
Paso 3: Sustituimos cada una de las columnas de las incógnitas por la matriz de términos independientes
Paso 3.1: Para x sustituimos la primera columna por la de términos independientes pues x es la primera incógnita:
Calculamos el determinante de
la nueva matriz
Esta es la solución
para x
Dividimos
entre el
determinante
del paso 2

38. 38
Regla de Cramer
Paso 3.1: Repetimos lo mismo pero ahora en la segunda columna para y.
● Sustituimos la segunda columna por la matriz de términos independientes
● Obtenemos el determinante de esta nueva matriz
● Dividimos entre el determinante de la matriz de coeficientes
Paso 3.2: Repetimos lo mismo pero ahora en la segunda columna para z.
z=
Recuerda: Para
calcular los
determinantes
podemos utilizar el
método de Cofactores
o la regla de Sarrus.
Solución
de y
Solución
de z

39. Ya tenemos las soluciones de nuestras incógnitas:
x = 1 y = 7 z = -2
39
Regla de Cramer
Vamos a comprobar nuestros resultados para saber que están correctos
Sustituimos los resultados de cada variable en las ecuaciones y nos deben resultar verdaderas
Podemos ver que TODAS las ecuaciones son verdaderas cuando sustituimos los valores y
resolvemos las operaciones.
Hemos terminado de resolver nuestro sistema de ecuaciones mediante la regla de CRAMER

40. 40
Fin de la semana 1

41. Bibliografía
41
• Grossman, S. (s.f.). Álgebra Lineal. Mc Graw Hill.
• Monsalve, S. (2009). Matemáticas básicas para economistas: Álgebra Lineal con
notas históricas y contextos económicos. Bogotá: Universidad Nacional de
Colombia. Facultad de Ciencias Económicas.
• Valle, J. d. (s.f.). Álgebra Lineal y sus aplicaciones. McGraw Hill. E
Figura 1. Avendaño A. (2020). Matriz: Multiplicación. 21/05/2020, de Geogebra Sitio
web: https://www.geogebra.org/m/S6R8A2xD
Figura 2. Descartes 3D. (2006). Producto de una matriz . 21/05/2020, de Creative Commons Sitio
web:
http://recursostic.educacion.es/descartes/web/materiales_didacticos/matrices/matrices_operacio
nes_II. htm
Figura 3. Katz, Victor (2004). Pearson Education, ed. A History of Mathematics. Sitio
web: https://es.wikipedia.org/wiki/Regla_de_Craer