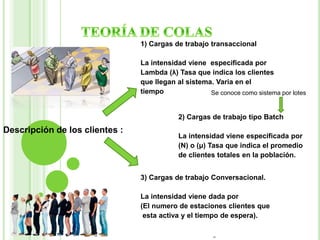
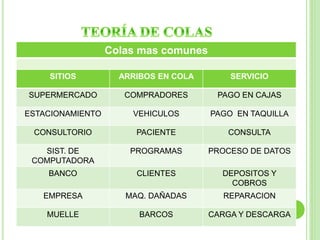
Este documento presenta los conceptos básicos de la teoría de colas y su aplicación para analizar el sistema de pago en la taquilla de un estacionamiento. Explica que los clientes esperan en promedio 3 minutos en la cola, mientras que la tasa de llegada de clientes es de 45 por hora y la tasa de servicio es de 60 clientes por hora. Resuelve que el tiempo promedio que un cliente pasa en el sistema es de 4 minutos, con 3 minutos en la cola y 1 minuto de servicio, y que el número promedio de clientes en el sistema en un momento

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
INSTITUTO UNIVERSITARIO DE TECNOLOGÍA INDUSTRIAL
CÁTEDRA: MODELOS MATEMÁTICOS
ESPECIALIDAD: ADMINISTRACIÓN INDUSTRIAL
PROFESOR:
GINO MARTÍNEZ
ESTUDIANTES:
MAYRALEJANDRA ACURERO
OSLEYDI ARTEAGA

3. Aplicable:
Negocios comercios
Transporte
telecomunicaciones

5. Elementos existentes en la teoría de cola
1. Proceso básico de colas
2. Fuente de entrada o población potencial
3. Cliente
4. Capacidad de la cola
5. Disciplina de la cola:
FIFO: primero en entra- Primero en salir
LIFO: último en llegar primero en salir
RSS: selección aleatoria
6. Mecanismo de servicio
7. Redes de colas
8. Proceso de servicio

6. Objetivos:
 Identificar el nivel óptimo de capacidad del sistema que minimiza el coste
del mismo.
 Evaluar el impacto que las posibles alternativas de modificación de la
capacidad del sistema tendrían en el coste total del mismo.
 Establecer un balance equilibrado (“óptimo”) entre las consideraciones
cuantitativas de costes y las cualitativas de servicio.
 Hay que prestar atención al tiempo de permanencia en el sistema o en la
cola: la "paciencia" de los clientes depende del tipo de servicio específico
considerado y eso puede hacer que un cliente "abandone" el sistema.

7. Descripción de los clientes :
1) Cargas de trabajo transaccional
La intensidad viene especificada por
Lambda (λ) Tasa que indica los clientes
que llegan al sistema. Varia en el
tiempo
Se conoce como sistema por lotes
2) Cargas de trabajo tipo Batch
La intensidad viene especificada por
(N) o (μ) Tasa que indica el promedio
de clientes totales en la población.
3) Cargas de trabajo Conversacional.
La intensidad viene dada por
(El numero de estaciones clientes que
esta activa y el tiempo de espera).
çç

8.  λ = Lambda
 μ = My / miu
Terminología
 Consiste en una regla de
transformación simple (sustitución de
variable) y un esquema simple para
definir funciones.
 En probabilidad y estadística, es la
medida o valor esperado de una
distribución

9. Ejercicio de teoría de colas
Enunciado:
Supongamos que en el estacionamiento del CENTRO COMERCIAL GUACARA PLAZA,
cuenta con una sola persona para ofrecer servicios en la taquilla de pago, donde
llegan en promedio de 45 clientes por hora y se tiene capacidad para atender 60
clientes por hora. Sabiendo que los clientes esperan en promedio 3 minutos en la
cola.

10.  Se pide:
 A) Calcular el tiempo promedio que un cliente pasa en el
sistema
 B) Calcular Numero promedio de clientes en el sistema en el
momento dado
 Sabiendo que:
 λ: Tasa promedio de la cantidad de llegadas de nuevos
clientes
 μ: Tasa promedio de la cantidad total de clientes en la taquilla
de pago
 Ws: Tiempo promedio de clientes que pasa en el sistema
 Wq: Tiempo promedio de cliente que pasa en la cola
 Ls: Numero promedio de clientes en el sistema.

11.  Datos:
λ= 45 clientes
μ= 60 clientes Total
Wp= 3 min. En la cola
Ws= ?
Ls= ?
λ= 45 Clientes / 60 Min = 0,75
Si llegan 45 por hora lo dividimos entre 60 min que tiene
la hora y eso nos dará los clientes que llegan por min.
μ= 60 Clientes / 60 Min = 1
Si en total pueden ser atendidos 60 clientes por hora
tomamos ese total y lo dividimos entre 60 min que tiene
la hora y nos dará el numero de clientes que llegan en
servicio por min en una hora
 Datos:
λ= 45 clientes = 0,75 Clientes
μ= 60 clientes Total = 1
Wp= 3 min. En la cola = 3
Ws= ?
Ls= ?

12.  Se pide:
 A) Calcular el tiempo promedio que un cliente pasa en el sistema
Solución: A) Ws = Wq + μ
Ws= ?
Ws =Wq+¹/μ
Ws = 3+¹/¹ =3+1 =4
Es decir que el tiempo promedio que un cliente pasa en el sistema de pago de
la taquilla del estacionamiento es de 4 Min c/u
Se distribuye asi:
3 Min pasa esperando en la cola
1 Min de Servicio.
 Datos:
λ= 45 clientes = 0,75
μ= 60 clientes Total = 1 Min
Wp= 3 min. En la cola
Ws= ?
Ls= ?

13.  Se pide:
 B) Calcular Numero promedio de clientes en el sistema en el momento
dado.
Solución: B) Ls= λ * Ws
Ls= ?
Ls = λ * Ws
Ls = 0,75 * 4 = 3
Es decir que los clientes que se encuentran en la cola son 3 Clientes ya que
se ha dicho que solo tenemos un servidor disponible.
Se distribuye así:
1 cliente puede estar pagando el servicio
2 Clientes están en la cola. EN ESPERA.
 Datos:
λ= 45 clientes = 0,75
μ= 60 clientes Total = 1 Min
Wp= 3 min. En la cola
Ws= 4 clientes
Ls= ?
 Datos:
λ= 45 clientes = 0,75
μ= 60 clientes Total = 1 Min
Wp= 3 min. En la cola
Ws= 4 min de espera
Ls= 3 clientes se encuentran
en cola

14.  Interpretación de resultados:
 A) Calcular el tiempo promedio que un cliente pasa en el sistema
 B) Calcular Numero promedio de clientes en el sistema en el momento dado.
 Datos:
λ= 45 clientes = 0,75
μ= 60 clientes Total = 1 Min
Wp= 3 min. En la cola
Ws= 4 min de espera
Ls= 3 clientes se encuentran
en cola
A) Calcular el tiempo promedio que un
cliente pasa en el sistema.
El tiempo promedio de un cliente que
pasa en la taquilla de pago 3 min en la
cola y un min para pagar el servicio.
B) Calcular Numero promedio de
clientes en el sistema en el momento
dado.
El número promedio en el sistema es 1
esta pagando en taquilla mientras dos
están haciendo la cola.

15. Colas mas comunes
SITIOS ARRIBOS EN COLA SERVICIO
SUPERMERCADO COMPRADORES PAGO EN CAJAS
ESTACIONAMIENTO VEHICULOS PAGO EN TAQUILLA
CONSULTORIO PACIENTE CONSULTA
SIST. DE
COMPUTADORA
PROGRAMAS PROCESO DE DATOS
BANCO CLIENTES DEPOSITOS Y
COBROS
EMPRESA MAQ. DAÑADAS REPARACION
MUELLE BARCOS CARGA Y DESCARGA