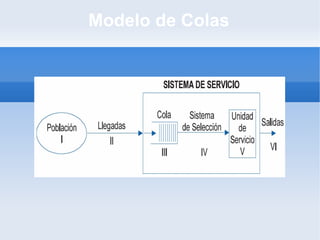
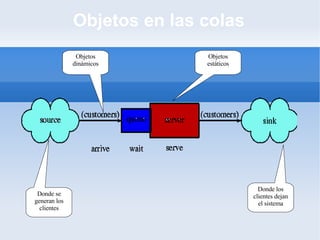
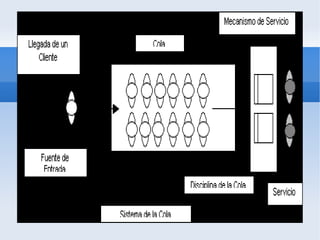
El documento describe el modelo de colas de sistemas operativos. Explica los conceptos básicos como elementos, fuentes, gestión y notación de colas. Describe el modelo M/M/1, incluyendo variables de estado como tasa de llegada, tasa de servicio, factor de utilización, número promedio de unidades y probabilidades. Finalmente, presenta un ejercicio sobre una secretaria que mecanografía cartas para calcular probabilidades usando este modelo.

1. MODELO DE COLAS SISTEMAS OPERATIVOS

2. Modelo de Colas

3. Objetos en las colas Donde se generan los clientes Donde los clientes dejan el sistema Objetos dinámicos Objetos estáticos

4. Elementos Población Fuente: Finitas Ejm: Equipos a reparar Infinitas Ejm: Carros a lavar Proceso de llegada: Determinístico Probailístico Características de la Cola Finita Infinita

6. Gestión de las Colas FIFO LIFO Por prioridades Tiempo de servicio mayor. Tiempo de espera mayor. SRR

7. 5. Unidades de Servicio Servidor único (servicio único monofase). Servidores en tandem (servicio multifase o servicio con múltiples operaciones). Múltiples servidores monofásicas en paralelo. Múltiples estaciones multifásicas en paralelo. Sistemas mixtos.

8. Notación Kendal Por convención los modelos que se trabajan en teoría de colas se etiquetan A / B / C A = distribución de llegada B = distribución del servicio C = Número de canales de servicio M Markov Distribución = D Determinista G General

9. Modelo M/M/1 Si en un periodo T, existe λ llegadas en promedio, entonces la probabilidad de n llegadas en el mismo periodo esta dado por: Si μ es la tasa de servicio promedio, entonces la probabilidad de que el tiempo de servicio sea t , está dado por: f(t) = μ e - μ t

10. Variables de estado λ tasa media de llegadas por unidad de tiempo. μ tasa media de servicio (número medio de servicios completados por unidad de tiempo). ρ factor de utilización de la unidad de servicio. N número de unidades en el sistema. P n probabilidad de que cuando una unidad llega al sistema para recibir servicio haya n unidades en el sistema. Ls número medio de unidades en el sistema. L q Número esperado de clientes en la cola Ws tiempo medio de estancia en el sistema para cada unidad (tiempo de espera + tiempo de servicio). W q Tiempo esperado de espera en la cola o tiempo medio de espera en la cola (desde que llega hasta que empieza a ser servido).

11. Formulas Generales para el Modelo M/M/1

12. Uso del Sistema λ tasa media de llegadas. unidades/tiempo μ tasa media de servicio. unidades/tiempo ρ factor de utilización / número medio de unidades atendidas por momento / probabilidad de que el sistema esté ocupado λ ≤ μ ¿qué pasaría si λ > μ ? Pw = ρ = λ / μ Prob. que el sistema esté ocupado. P(0) = 1 - ρ Prob. que el sistema esté vacío. P(n) = (1 - ρ ) ρ n Prob. que el sistema esté ocupado con n unid.

13. Ejercicio Debido a un reciente incremento en el negocio una secretaria de una cierta empresa tiene que mecanografiar 20 cartas por día en promedio (asuma una distribución de Poisson). A ella le toma aproximadamente 20 minutos mecanografiar cada carta (asuma una distribución exponencial). Suponiendo que la secretaria trabaja 8 horas diarias. Calcule la probabilidad de que la secretaria tenga más de 5 cartas que mecanografiar. Calcular: λ, μ, p, Lq , Wq, P(n)