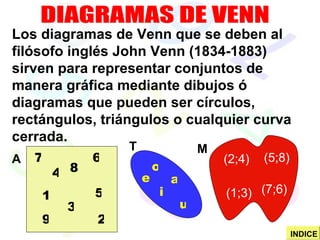
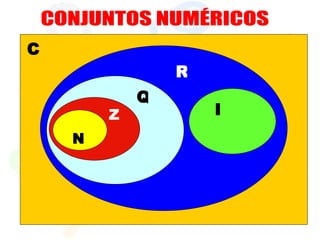
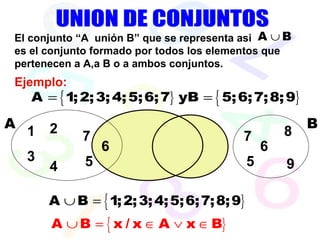
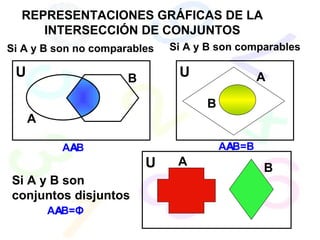
Este documento trata sobre la teoría de conjuntos. Introduce conceptos básicos como elementos, pertenencia a conjuntos, notación de conjuntos, determinación de conjuntos, diagramas de Venn, operaciones entre conjuntos como unión, intersección y diferencia. También define conjuntos numéricos y especiales como el conjunto vacío y conjunto potencia. Finalmente, presenta algunos problemas para practicar conceptos como expresar conjuntos por comprensión y calcular cardinalidad y operaciones entre conjuntos.



























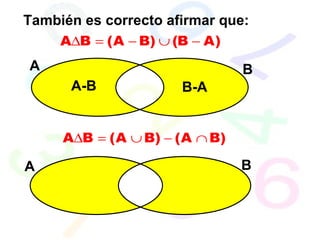













![A B C A B C A B C A B C [(A B) – C] [(B C) – A] [(A C) – B] ](https://image.slidesharecdn.com/conjuntos-110626205831-phpapp02/85/Teoria-de-Conjuntos-51-320.jpg)
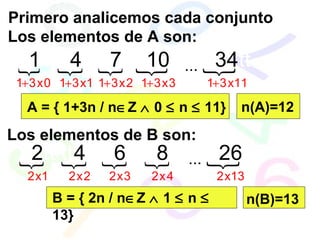
![A B A B C Observa como se obtiene la región sombreada Toda la zona de amarillo es A B La zona de verde es A B Entonces restando se obtiene la zona que se ve en la figura : (A B) - (A B) C Finalmente le agregamos C y se obtiene: [ (A B) - (A B) ] C ( A B ) C =](https://image.slidesharecdn.com/conjuntos-110626205831-phpapp02/85/Teoria-de-Conjuntos-52-320.jpg)



![FIN Profesor: Rubén Alva Cabrera [email_address]](https://image.slidesharecdn.com/conjuntos-110626205831-phpapp02/85/Teoria-de-Conjuntos-56-320.jpg)