Este documento trata sobre la teoría de conjuntos. Define conceptos básicos como conjunto, elemento, pertenencia, diagrama de Venn, determinación de conjuntos, relaciones entre conjuntos como inclusión e igualdad. También explica operaciones entre conjuntos como unión, intersección, diferencia y complemento, y presenta sus propiedades.

1. 1
MATEMATICA APLICADO A LA
MEDICINA
TEMA
TEORIA DE CONJUNTOS
2014

2. 2
CONJUNTO:
Idea Intuitiva:
La palabra conjunto sugiere de inmediato la idea de:
 Grupo
 Colección
 Selección
 Asociación
 Agregado , etc.
NOTACION
Para representar un conjunto se utilizan letras Mayúsculas,
tales como A , B , C .......
LA TEORIA DE CONJUNTOS

3. 3
ELEMENTO :
Son los objetos que forman parte del conjunto la propiedad fundamental de un
elemento es la pertenencia ; que se simboliza así
 : Se lee : “ pertenece a ”
A los elementos se les designa con letras minúsculas , tales como x , y , z
etc.
 Si un elemento x forma parte del conjunto A, entonces, ese elemento
pertenece a ese conjunto A así denotamos :
x  A : Se lee: “ x pertenece a A”
 Si un elemento x no forma parte del conjunto A, entonces, ese
elemento no pertenece a ese conjunto A. Así denotamos :
x  A : Se lee: “ x no pertenece a A”
Ejemplo: Sea A = { x , y , z }
x  A y  A z  A m  A
LA TEORIA DE CONJUNTOS

4. 4
Diagrama de Veen - Euler :
Consisten en representar a los conjuntos por medio de figuras geométricas
planas y cerradas en cuyo interior se ubican los elementos.
Ejemplo: A = {m , n , p }
.m
.n
.p
A
LA TEORIA DE CONJUNTOS

5. 5
Determinación de un conjunto :
Un conjunto se puede determinar:
por extensión y por comprensión
Por extensión :
Nombrando uno a uno los elementos del conjunto
Ejemplo: A = { 2, 4, 6, 8, 10 }
B = { a, e, i, o, u }
Por Comprensión :
Enunciando una propiedad o característica común a los elementos del
conjunto.
Ejemplo: A = {x  x es un número par }
B = { x / x son las vocales }
LA TEORIA DE CONJUNTOS

6. 6
El Conjunto de Números Naturales ( N)
N = { 1 , 2 , 3 ,4 , .................. }
En este conjunto sólo se puede efectuar operaciones de adición y
multiplicación sin restricciones.
CONJUNTOS NUMERICOS
El Conjunto de Números Enteros ( Z )
Son los números naturales precedidos por el signo - o + , incluyendo
el cero.
Z = { ............... – 3 , , - 2 , - 1 , 0 , 1 , 2 , 3 , .................. }
Donde N  Z
Z

7. 7
El Conjunto de Números Racionales ( Q)
Q = { x / x = ; a , b  Z ; b  0 }
Es decir el conjunto Q resulta de dividir 2 números enteros , con el
divisor diferente de cero . Y puede obtenerse.
CONJUNTOS NUMERICOS
b
a








mixtoPeriódico
puroPeriódico
inexactoDecimal
exactoDecimal
decimalNúmero
Q
Z

8. 8
Conjunto de Números Irracionales( Q )
Son aquellos números que no pueden expresarse en la forma ; b  0
a , b  Z , es decir que no presentan periodicidad en sus cifras decimales.
CONJUNTOS NUMERICOS
b
a
 ..........2,e,,2,3..,.......... 3
Q=
Conjunto de Números Reales ( R )
R = Q  Q
Nota:
Existe una correspondencia biunívoca entre los elementos del conjunto
de números reales y el conjunto de puntos de la recta .
PiP2P1
(x1) (x2) (xi)- +

9. GRAFICA CONJUNTISTA
9
R
Q
Z
N
Q´

10. 10
El Conjunto de Números Complejos ( C )
Al resolver la ecuación :
CONJUNTOS NUMERICOS
1icon;1-sidonde,
R1x01x
2
2


i
i se llama unidad imaginaria
Por lo tanto :
Un número Complejo podemos escribir en la forma a + bi ; a ,b  R
Luego :
C = { a + bi  a , b  R ; i2 = - 1 }

11. 11
Conjuntos Especiales :
 Conjunto Unitario : Es el conjunto que tiene un solo elemento.
Ejemplo: M = { x } ; N = { x  N  1 < x < 3 }
 Conjunto Nulo o Vacío : Es el conjunto que carece de elementos.
Denotado por 
Ejemplo: P = { x  N  1 < x < 2 } = 
 Conjunto Finito: Es el conjunto formado por un numero determinado de
elementos.
Ejemplo: M = { x  x es número dígito par menor que 40 }
 Conjunto Infinito: Es el conjunto formado por un numero indeterminado
de elementos.
Ejemplo: N = { x  R  1 < x  5 }
 Conjunto Universal : Constituido por todos los elementos de una
determinada materia.
El conjunto Universal no está definida en forma única, podemos elegir a
nuestra conveniencia. Se denota por la letra U
Ejemplo: Sea el universo U = { a , e , i , o , u }
LA TEORIA DE CONJUNTOS

12. 12
Relaciones entre Conjuntos :
LA INCLUSION
Ejemplo: Sea A = {2 , 3 , 5} y B = {1 , 2 , 3 , 4 , 5 , 6 }
.1
.4
.6.2 .3
.5
A
B
LA TEORIA DE CONJUNTOS
B
.2
.3
.5
.1
.4 B
.6
A

13. 13
Subconjunto Propio o Parte Propia:
Se dice que un conjunto A es subconjunto propio de o parte propia de B ; sí y
solo si, todos los elementos de A pertenecen a B , existiendo elementos de B
que no pertenecen a A ; se denota así:
A  B se lee: A es subconjunto propio de B
Nota: El conjunto nulo es subconjunto de todo conjunto .
  A ;  A
LA TEORIA DE CONJUNTOS
.1
.2
.3
BA

14. 14
Propiedades de la Inclusión:
LA TEORIA DE CONJUNTOS

15. 15
Igualdad de Conjuntos :
A y B son iguales , cuando están formados por los mismos elementos.
Y definimos así:
Ejemplo:
A = { x , y } y B = { y , x }
A = B
LA TEORIA DE CONJUNTOS

16. 16
Relaciones entre Conjuntos :
Conjuntos Comparables
.b
.d .f
Tienen algunos elementos en común.
A = { a , b , c , d } y B = { a , c , e , f }
A B
ABBABacomparableesA 
Conjuntos no comparables
ABBABABacomparableesnoA 
.e
Conjuntos Disjuntos:
 BAdisjuntossonByA No tienen ningún
elemento en común
LA TEORIA DE CONJUNTOS
.a
.c

17. 17
Conjunto de conjuntos o familia de conjuntos :
Es el conjunto que tiene como elementos a otros conjuntos.
Ejemplo: A= { {1 , 2 } , { 0 } , { 3 } }
LA TEORIA DE CONJUNTOS
Conjunto Potencia
Es el conjunto cuyos elementos son todos los subconjuntos de ese
conjunto , incluyendo el mismo y el nulo.
Dado un conjunto A ; el conjunto potencia de A, se denota por P(A)
Luego :
Ejemplo: Sea A = {a , b}
P(A) = { {a } , { b } , { a , b } ,  }

18. 18
Nota :
1. Si A tiene “ n” elementos, el número de elementos de la P(A) es igual
a 2n elementos.
P(B)P(A)BASi4.
P(B)P(A)BASi3.
}{)P(ASi2.


 
LA TEORIA DE CONJUNTOS
El conjunto potencia de A es una familia de conjuntos

19. 19
OPERACIONES ENTRE CONJUNTOS
Unión o Reunión de Conjuntos
Dado dos conjuntos A y B , se tiene : A  B = { x/ x  A  x  B }
A B Si A y B son no comparables , entonces:
A  B gráficamente es:
 Si A y B son comparables , entonces:
A  B es:
B
B
A
A

20. 20
OPERACIONES ENTRE CONJUNTOS
Propiedades de la Reunión de Conjuntos
n21i
n
1i
A...........AAA12.
DBCADCBASi11.
BBABASi.10
BABASi9.
B)(ABB)(AA8.
UUA7.
C)(BC)(ABASi6.
C;C)A(B)A(C)B(A5.
AA4.
C)B(ACB)(A3.
ABBA2.
A;AAA.1
















21. 21
OPERACIONES ENTRE CONJUNTOS
Intersección de Conjuntos
Dado dos conjuntos A y B , se tiene : A  B = { x/ x  A  x  B }
A B
 Si A y B son no comparables , entonces:
A  B gráficamente es:
 Si A y B son comparables , entonces:
A  B es: A
 Si A y B son Disjuntos
A  B es:
B
B
A
A
 BA

22. 22
OPERACIONES ENTRE CONJUNTOS
Propiedades de la Intersección de Conjuntos
A...........AAA13.
AB)(AA;AB)(AA12.
C)(AB)(AC)(BA
C)(AB)(AC)(BA11.
P(B)P(A)B)P(A10.
CBADBCASi9.
BB)(AAB)(A8.
CBCABASi7.
ABABASi6.
A5.
AUA4.
C)B(ACB)(A3.
ABBA2.
A;AAA.1
n21i
n
1














i
D


23. 23
OPERACIONES ENTRE CONJUNTOS
Diferencia de Conjuntos
Dado dos conjuntos A y B , se tiene : A - B = { x/ x  A  x  B }
Gráficamente , mediante el diagrama
de Veen se tiene:
A B
 Si A y B son no comparables , entonces:
A - B es:
 Si A y B son comparables , entonces:
A - B =  (No hay gráfico)
BA
B
A
B – A es:

24. 24
OPERACIONES ENTRE CONJUNTOS
Propiedades de la Diferencia de Conjuntos
B-C)-A(C-B)-(A12.
DisjuntossonA-B;BA;B-A11.
C)(AB)(AC)(B-A
C)-(AB)-(AC)(B-A10.
C,C)-(BC)-(ABASi9.
BABASi8.
C)(A-B)(AC)-B(A7.
B)-(AB6.
B)(A-AB-B)(AB)-(A5.
A-4.
AB-A3.
AA2.
A-A.1



















25. 25
OPERACIONES ENTRE CONJUNTOS
Complemento de un Conjunto
Dado el universo U y un conjunto A ; el complemento de A , denotado por
A O Ac se define asi :
Ac = { x/ x  U  x  A } = U - A
Ac
Gráficamente:
A
Si el conjunto referencial no es el conjunto universo, tal como B , donde
A  B ; entonces el complemento de A con respecto a B , denotado
por CB (A) Será :
CB (A) = { x / x  B  x  A } = B - A
U

26. 26
OPERACIONES ENTRE CONJUNTOS
Propiedades del Complemento
B)(AU)B(A12.
B)(A-U)B(A11.
BA)B(A
BA)B(A10.
ABBASi9.
B(A)C8.
A-B(A)C7.
6.
U5.
U4.
AA3.
UAA2.
A)A(.1
B
B













BABA




27. 27
Diferencia Simétrica
Dado dos conjuntos A y B ; la diferencia Simétrica , denotada por A  B se
define así:
A  B = (A – B ) U (B – A)
B
Gráficamente:
A
Ejemplo . Si A = { 2 , 3 , 5 } y B = { 0 , 1 , 2 , 3 , 8 , 9 } Hallar A  B
Solución.
Como A  B = (A – B )  (B – A) = { 5 }  { 0 , 1 , 8 , 9 }
A  B = { 0 , 1 , 5 , 8 , 9 }

28. 28
Propiedades de la Diferencia simétrica
   
 
CBCABASi9.
)AB()BA(BΔA8.
B)(A-B)A(BΔA7.
C)B(A-)BA(CBB)Δ(A6.
C)BΔ(C)A(CB)Δ(A5.
BA4.
ABΔBΔA3.
AA2.
AA.1









C
CBAC



29. 29
TEORIA DE CONJUNTOS
Número de Elementos de un Conjunto
Al número de elementos de un conjunto se le llama :
Cardinal de un Conjunto y se denota así:
Para un conjunto A se tiene n(A) ó Card (A)
Ejemplo . Si A = { a , e , i , o , u }
 n(A ) = 5
ó
n [ P(A) ] = 25 = 32

30. 30
TEORIA DE CONJUNTOS
Propiedades
C)Bn(AC)n(B-C)n(A-B)n(A-n(C)n(B)n(A)C)Bn(A
:entonces,CBA
:quetaless,comparablenoconjuntossonCyB,ASi4.
B)n(A-n(B)n(A)B)n(A
:entoncess,comparablenoconjuntossonByASi3.
B)n(A-n(A)B)-n(A
:racualesquieconjuntossonByASi2.
n(B)n(A)B)n(A
:entonces,disjuntosconjuntossonByASi.1







31. 31
EJERCICIOS DE CONJUNTOS
1. Para la gráfica de A , B y C se tiene:
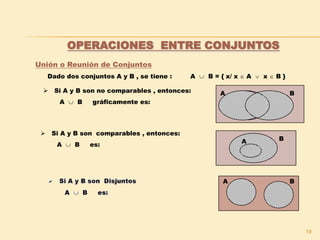
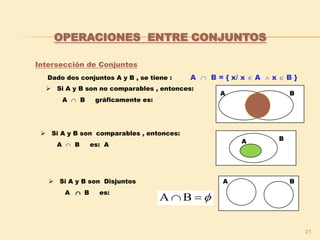
Las operaciones que representan las regiones:
A B
C
R1
R4
R5
R7
R2
R6
R3
R8
U
)BCn(A]BC)n[(An(B)C)n(AR
)BAn(C)B(An[CB)n(An(C)R
)CAn(B])C(ABn[C)n(An(B)R
)CBn(A])C(Bn[AC)n(Bn(A)R
4
3
2
1





32. 32
EJERCICIOS DE CONJUNTOS
Para la gráfica de A , B y C se tiene:
Las operaciones que representan las regiones:
A B
C
R1
R4
R5
R7
R2
R6
R3
R8
U
)CBn(AR
C)Bn(AR
)ACn(B]AC)(Bn[n(A)C)n(BR
)CBn(A]C)n[(An(C)B)n(AR
8
7
6
5



 B

33. 33
EJERCICIOS DE CONJUNTOS
2. Sean los conjuntos:
A = { 1 , 2 , 3 , 4} ; B = { 0 , 2 , 5 , 6} y C = { 1 , 2 , 4 , 6 , 7 }
con U ={ 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }
Hallar :
Solución:
      )B'A(CBA3.BCA2.CBA1. 


           71,2,4,6,77,8,91,2,4,6,75,60,1,2,3,4,CBA.1 




           66,5,2,0)7,63(BA)(CC)(ABCA.2 
     9,8,7,6,5,3,2,1,09,8,7,6,5,3,1,02)BA(C)B(A.3 

34. 34
EJERCICIOS DE CONJUNTOS
3. Si los conjuntos A y B tienen los siguientes datos:
n(AB) = 60 ; n(A – B) = 24 y n(B  A ) = 20 Hallar: n(A) + n(B)
Solución:
......(1)60B)n(A-n(B)n(A):tieneSe
B)n(A-n(B)n(A)B)n(A:queSabemos


......(2)..........24B)n(A-n(A)
B)n(A-n(A)B)n(A:queSabemos


......(3)..........20B)n(A-n(B)
A)n(B-n(B)A)n(BA-BABComo


Restando : (1) y (2) se tiene : n(B) = 36
Restando : (1) y (3) se tiene : n(A) = 40
Luego n(A) + n(B) = 40 + 36 = 76

35. 35
EJERCICIOS DE CONJUNTOS
4.Dado los conjuntos: A = { a , {a , b} } ; B = { a , b , { c } } ; C = A – B
Hallar : a) P(A  C) b) P(A)  P(B)
Solución:
        
      ,,C)P(Aba,CAa.
entonces,ba,BACcb,a,B;ba,a,A:Como
ba

        
                  
  ,aP(B)P(A)
,,,,,,,,,,,,aP(B)
,,,,,aP(A)b.






cbacbcabacb
baaba

36. EJERCICIOS DE CONJUNTOS
7
a
b
c
18-a-b 26-b-c
33-a-c

37. 37
6. En una encuesta realizada en un centro hospitalario de Lima ,
conformado por 60 profesionales de la salud se tiene la siguiente
información : 40 profesionales hablan inglés ; 28 hablan el francés,
16 hablan alemán; 12 hablan el inglés y el francés 5 el inglés y el
alemán, los tres idiomas sólo 2. Si el número de profesionales que
hablan sólo el francés es igual al número de profesionales que hablan
el francés y el alemán. ¿Cuántos hablan únicamente el francés?
Solución:
x)IFn(A
2I)Fn(A5A)n(I
12F)n(I16n(A)
28n(F)40n(I)




I F
A
25
3
2
10
x
16-(3+2+x)
28-(10+2+x)
EJERCICIOS DE CONJUNTOS

38. EJERCICIOS DE CONJUNTOS
7. De una población de 50 ingresantes a la
facultad de medicina de la UPSM se sabe
que:
* 5 mujeres tienen 17 años.
* 16 mujeres no tienen 17 años.
* 14 mujeres no tienen 18 años.
* 10 hombres no tienen 17 ni 18 años.
¿Cuantos hombres tienen 17 o 18 años?
38

39. 39
SOLUCIONARIO
Hombres Mujeres
17 años
A
5
p
18 años
10
B
q
Mujeres que no tienen 18 años:
p + 5 = 14 p = 9
Mujeres que no tienen 17 años
:
p + q = 16 q = 7
10 + ( A + B ) + 5 + 7 + 9 = 50
Luego:
A + B = 19

40. EJERCICIOS DE EXAMENES
TEMA: CONJUNTOS

41. EJERCICIOS DE EXAMENES
TEMA: CONJUNTOS
3. Hay tres centros de Salud “A”, “B” y “C” que pueden atender a una población
de 3000 familias Se obtuvo la siguiente información: 1 800 familias se atienden en
el centro de salud “A”, 1 700 familias se atienden en el centro de salud “B”, 1 200
familias se atienden en el centro de salud “C”, 1 250 familias se atienden en los
centros de salud “A y B”, 700familias en los centros de salud “A y C”, 600 familias
se atienden en los centros de salud “B y C” y 200 familias en los tres centros de
salud. ¿Cuál es el numero de familias que no se atienden en los centros de salud
“B o C” ?
A) 50 B) 650 C) 700 D) 200 E) 550