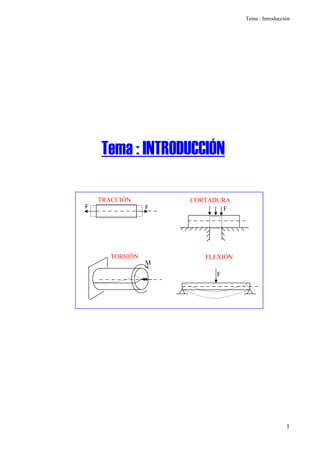
El documento introduce conceptos básicos sobre tensiones en materiales. 1) Se define tensión como las fuerzas internas que aparecen en un sólido deformable debido a fuerzas externas. 2) Las tensiones se pueden descomponer en tensión normal, la componente a lo largo de la normal de la superficie cortada, y tensión cortante, la componente tangencial. 3) En un punto dado, el estado de tensiones depende de la orientación de la superficie cortada, pudiendo haber diferentes valores de tensión.

1. Tema : Introducción
Tema : INTRODUCCIÓN
TRACCIÓN CORTADURA
F F F
TORSIÓN FLEXIÓN
M
F
1

2. Tema: Introducción
I.1.- INTRODUCCIÓN A LA RESISTENCIA DE MATERIALES
La MECÁNICA estudia los SÓLIDOS RÍGIDOS
La RESISTENCIA DE MATERIALES estudia los SÓLIDOS DEFORMABLES
Se propone el siguiente ejemplo:
Se quiere levantar un cuerpo de 100 Kg de peso y para hacer menor el esfuerzo a realizar, se
utiliza una barra, que a través de un apoyo intermedio O, se usará como una palanca. Se desea
en un principio calcular el esfuerzo P que se deberá aplicar en el extremo de la barra
P
100 Kg
O
1m 2m
Fig. I.1.a
Suponiendo la barra utilizada, como rígida, es la Mecánica la que resuelve el problema. Así
por la ecuación de equilibrio:
∑M O =0 P.2 = 100.1 → P = 50 Kg
Pero la barra, en realidad, es un sólido deformable y como tal, podría ocurrir que se rompiese
o que se deformase demasiado y por tanto no nos sirviese para elevar el peso de 100 Kg.
100 Kg
La barra se rompe
O P
1m 2m
Fig. I.1.b
100 Kg
La barra se deforma demasiado
O P
1m 2m
Fig. I.1.c
Será precisamente la RESISTENCIA DE MATERIALES la que nos ayude a dimensionar la
barra a utilizar, para evitar que se rompa o que se deforme demasiado
2

3. Sección I1: Introducción a la Resistencia de Materiales
¡ Que no se rompa la barra ¡
Las fuerzas exteriores que aplicamos sobre los cuerpos, provocan en ellos fuerzas interiores
o tensiones que se oponen a las exteriores. Ello es debido porque las fuerzas exteriores alteran
las posiciones de reposo que mantenían las partículas elementales del interior del cuerpo y se
desarrollan entonces fuerzas internas que tratan de recuperar las posiciones iniciales de las
mismas
Fint Fint Fext
Fext
en reposo
Fig. I.2
Al aumentar el valor de las fuerzas exteriores aumentará el valor de las fuerzas interiores y
ello sucederá así hasta que éstas llegan a su valor límite y ya no pueden crecer más. A partir
de aquí el sólido romperá.
F1int
F1ext
F2int>F1int
F2ext>F1ext
F3int=Fint max>F2int
F3ext>F2ext
La barra se rompe
F4ext>F3ext
Fig. I.3
Se denomina resistencia mecánica de un cuerpo: “a las fuerzas internas máximas o
tensiones que es capaz de desarrollar dicho cuerpo”. Dependerá de las dimensiones del
mismo y del material del que esté hecho.
¡ Que no se deforme demasiado la barra ¡
En el ejemplo gráfico anterior, se observa que a medida que se va aumentando la fuerza
externa, el cuerpo se va deformando más. Se tendrá que controlar que los sólidos no se
deformen demasiado y dejen de ser útiles.
Se denomina rigidez de un cuerpo: “a la resistencia que presenta a dejarse deformar”
Conclusión final:
La RESISTENCIA DE MATERIALES permitirá calcular:
• Las fuerzas internas o tensiones. (A través de ellas se controlará que los cuerpos no se
rompan)
• Las deformaciones. (A través de ellas se controlará que los cuerpos no se deformen
demasiado)
3

4. Tema: Introducción
I.2.-PRINCIPIOS GENERALES EN LOS QUE SE VA A BASAR LA RESISTENCIA
DE MATERIALES
A continuación se enunciarán tres Principios que aplicaremos en la mayor parte de la
Resistencia de Materiales y que servirán para simplificar los cálculos
Principio de los Pequeños Desplazamientos
Según este Principio, se admite que al aplicar las fuerzas exteriores sobre los cuerpos, los
desplazamientos que se originan, son en la mayoría de los casos pequeños en relación con las
dimensiones de los mismos. Ello nos permitirá que las ecuaciones de equilibrio de la Estática
las podamos aplicar sobre el cuerpo en su posición inicial, es decir sin haberse deformado.
Ejemplo: Sea una estructura formada por dos cables que soportan una carga. Se desea calcular
las tensiones en los cables
β
α
O
P
Fig. I.4.a
Al considerar la estructura deformable, las ecuaciones de equilibrio de fuerzas, se deberían
plantear, en rigor, en la estructura ya deformada. Es decir cuando los extremos inferiores de
las cuerdas y por tanto la carga P se ha trasladado al punto O´.
Estableciendo pues, las ecuaciones de equilibrio en el punto O´ se tendría:
β-∆β F2
α+∆α
F1
β-∆β
α+∆α
O´
O
P Fig. I.4.c
O´
P ∑F x =0 F2 .sen ( β − ∆β ) = F1 .sen (α + ∆α )
Fig. I.4.b
∑F y =0 F2 . cos( β − ∆β ) + F1 . cos(α + ∆α ) = P
Con estas ecuaciones de equilibrio no se podrán obtener los valores de F1 y F2 pues se
desconocen las variaciones ∆α y ∆β que han sufrido las inclinaciones de los cables.
4

5. Sección I.2: Principios Generales
Si se supone ahora que las deformaciones de los cables van a ser pequeñas y aplicamos el
“Principio de los Pequeños Desplazamientos”, las ecuaciones de equilibrio se aplicarán ahora
a la estructura de cables aún sin deformar (en el punto O) y se podrá resolver fácilmente el
valor de las tensiones en ambos cables.
β
α F2
β
F1
α
O
O P Fig. I.4.e
P ∑F x =0 F2 .sen β = F1 .sen α
Fig. I.4.d ∑F y =0 F2 . cos β + F1 . cos α = P
Con estas dos ecuaciones se obtienen los valores de F1 y F2
Observaciones:
Los valores obtenidos de F1 y F2 no serán exactamente los reales, pero tendrán una
aproximación suficiente pata considerarlos como válidos. A partir de ellos se podrá estudiar la
deformación de la estructura.
Si los desplazamientos de la estructura no fuesen tan pequeños, los resultados así obtenidos
no serían válidos y no se podría aplicar este Principio.
Este Principio se podrá aplicar en la mayor parte de los problemas que resuelve la Resistencia
de Materiales, ya que generalmente se trabajará con pequeñas deformaciones
Principio de la Superposición de los Efectos
Este Principio dice que: “ Los efectos producidos por varias cargas actuando sobre un
cuerpo (fuerzas internas o tensiones y deformaciones), se pueden obtener, siempre que las
deformaciones producidas sean pequeñas, como suna de los efectos producidos por cada
una de las cargas actuando separadamente”
= +
(1) (2)
tensiones = tensiones (1) + tensiones (2)
deformaciones = deformaciones (1) + deformaciones (2)
Fig. I.5
5

6. Tema: Introducción
Observaciones:
Este Principio es de gran utilidad y se aplicará también en muchos problemas de la
Resistencia de Materiales, dado que permite dividir el caso de una solicitación general de
cargas, que puede ser compleja, en casos sencillos que resultan haciendo actuar por separado
dichas cargas y así en muchos casos poder utilizar los Prontuarios que dan soluciones para
dichos casos simples de cargas.
Si las deformaciones producidas fuesen grandes este Principio no se podría aplicar. Éste sería
el caso, por ejemplo, de una viga de “gran esbeltez” (vigas de longitudes grandes y pequeñas
secciones) sometida a una carga de compresión y otra de flexión
F F
P P
≠ +
Fig. I.6.a Fig.I.6.b Fig.I.6.c
P actuando sola → acorta la viga (Fig. I.6.b)
F actuando sola → flexiona la viga (Fig. I.6.c)
P y F actuando juntas → F (flexiona la viga) y P (acorta la viga y la flexiona aún más)
(Fig. I.6.a)
Principio de Saint Venant
Este Principio dice: “Si se sustituye el sistema de fuerzas que está actuando sobre un cuerpo
por otro equivalente a él, los efectos que ambos sistemas producen (tensiones y
deformaciones) serán similares en todos los puntos del cuerpo, salvo en aquellos que se
encuentran en la zona próxima a donde estaban aplicadas las fuerzas”
F2
R = F1 +F2 +F3
F1
F3
Fig. I.7.a Fig. I.7.b
Según este Principio las tensiones y deformaciones producidas por las cargas en (Fig. I.7.a),
son las mismas que las que aparecerán en (Fig. I.7.b), salvo en la zona rayada, próxima a
donde actúan las cargas, que serán diferentes:
En la zona rayada: tensiones y deformaciones (Fig. I.7 a) ≠ tensiones y deformaciones (Fig.
I.7.b)
En el resto: tensiones y deformaciones (Fig. I.7.a) = tensiones y deformaciones (Fig. I.7.b)
6

7. Sección I.2: Principios Generales
Así, se podrá aplicar este Principio a problemas de Resistencia de Materiales en donde la
superficie donde actúa la carga, es pequeña en relación con las dimensiones de la pieza, pues
en este caso la zona afectada por el cambio (zona rayada) tendría poca consideración.
SI R=ΣF
→
Fig. I.8.a
NO R=ΣF
→
Fig. I.8.b
Como se observa en (Fig. I.8.a), la zona rayada (donde se van a producir las alteraciones en el
estado de tensiones y deformaciones), es pequeña, con lo cual la sustitución del sistema de
fuerzas por su resultante, apenas va a suponer alteración de dicho estado en la viga. No ocurre
lo mismo en el caso de (Fig. I.8.b), donde la zona rayada es grande y por tanto la zona donde
se van a dar las alteraciones en el estado de tensiones y deformaciones, al sustituir el sistema
de fuerzas por su resultante, es muy amplia, con lo cual no se podrá hacer dicha sustitución,
pues se cometerían errores graves en los cálculos.
7

8. Tema 1: Tensiones
Tema 1 : TENSIONES
F1
S
∆S u σ nS
F4 O ρ ∆F
τ
F2
1

9. Tema 1: Tensiones
1.1.- CONCEPTO DE TENSIÓN
Consideremos un sólido sometido a un sistema de fuerzas: F1, F2, F3, ..,Fn y que esté en
equilibrio estático (no se mueve) y en equilibrio elástico (ya está deformado).
F3
F1
S
F4 F5 Fn
F2
Fig. 1.1.a
Debido a las fuerzas exteriores aparecen en el interior del sólido las fuerzas
interiores, que se oponen a la acción de las exteriores y tratan de llevar al sólido a la
posición que tenía inicialmente de reposo. Para ponerlas de manifiesto seccionemos el
sólido por la superficie S.
F3
F1
S S
∆F
∆F Fn
F4 O O F5
∆S ∆S
F2
Fig. 1.1.b Fig. 1.1.c
Las dos partes en que ha quedado dividido el sólido no estarían ahora en equilibrio. Para
reproducir dicho equilibrio se tendría que restablecer las acciones que cada parte del
sólido ejercía sobre la otra. Estas acciones son las fuerzas interiores (∆F), fuerzas que
las partículas de un lado de la superficie S ejercían sobre las del otro lado
Se denomina:
r
r ∆F
Tensión media en el punto O: ρ med =
∆S
r
r ∆F
Tensión en el punto O: ρ = lim ∆S →0 (1.1)
∆S
2

10. Sección 1.2: Tensiones normales y cortantes
1.2.- TENSIONES NORMALES Y CORTANTES
F1
S
∆S u σ nS
F4 O ρ ∆F
τ
F2
Fig. 1.2
r
r ∆F
Tensión en el punto O: ρ = lim ∆S →0
∆S
r
es un vector de la misma dirección y sentido que ∆F pero de menor módulo (va
dividido por ∆S)
r r
Tensión normal (σ ) : es la componente de la tensión ρ sobre la dirección normal a la
superficie S.
r r r r
Se obtendrá: σ = ρ .u σ = σ .u (1.2)
r
siendo u el vector unitario normal a la superficie S
r r
Tensión cortante (τ ) : es la componente de la tensión ρ sobre la propia superficie S
r r r
Se cumplirá que: ρ = σ +τ ρ = σ 2 +τ 2 (1.3)
r r r
con lo cual: τ = ρ −σ τ = ρ2 −σ 2 (1.4)
1.3.- ESTADO DE TENSIONES EN UN PUNTO
Si se hubiese seccionado el sólido por diferentes superficies S que pasen por el punto O
r
se hubiesen obtenido diferentes valores de la tensión ρ en dicho punto, puesto que las
acciones que se estaban ejerciendo sobre el punto O por parte de los que le rodean no
serían las mismas
F3
F1
ρ2
ρ3 ρ1 Fn
F4 F5
ρ4
F2 ρn
Fig. 1.3
3

11. Tema 1: Tensiones
Al conjunto de todos los valores de las tensiones ρ en un punto O, correspondientes a
todas las superficies que pasen por él, se le denomina: ESTADO DE TENSIONES DEL
PUNTO O
Así, según se ve en (Fig. 1.4.a y b), si seccionásemos por la superficie S1 actuaría la
tensión ρ1, si seccionásemos por la superficie Sn actuaría la tensión ρn, etc..Luego cada
tensión va asociada a una Superficie
F1 F1
S1 Sn
ρ1
F4 F4
F2 F2 ρn
Fig. 1.4.a Fig. 1.4.b
COMPONENTES DEL ESTADO DE TENSIONES EN UN PUNTO
De todas las tensiones que puede haber en un punto, se verá cómo, si seleccionamos 6
de ellas, a las que denominaremos “Componentes del estado de tensiones en un
punto”, a partir de ellas, se podrán conocer todas las demás.
Sea O un punto del sólido cuyo “Estado de tensiones” se quiere conocer. Aislemos un
elemento de volumen diferencial, en forma de paralelepípedo recto, con vértice en O,
origen de un sistema de ejes coordenados: x,y,z, coincidentes con las aristas del
paralelepípedo. Al ir reduciendo las dimensiones del paralelepípedo, manteniéndole
semejante a sí mismo, en el límite, el paralelepípedo tiende al punto O y todas sus caras
pasan por O, con lo cual se podrá considerar las tensiones sobre sus caras como
tensiones en el punto O.
F3
F1
y
O
F4 x F5 Fn
F2 z
Fig. 1.5
4

12. Sección 1.3: Estado de tensiones en un punto
Ampliemos el paralelepípedo y por lo visto en 1.2., sobre cada una de las caras de dicho
paralelepípedo habrá una tensión normal σ y una tensión cortante τ. Si descomponemos
ésta a su vez, en sus dos componentes sobre las direcciones de los ejes respectivos, se
tendrán 3 tensiones en cada una de las caras y por tanto 18 tensiones sobre el
paralelepípedo completo.
y σ´y
τ´yx
τ´yz
σz
τzx τ´xy
τxz dy
σx τ´zy σ´x
τzy
σ´z τ´zx τ´xz
τxy
O dx x
τyx τyz
dz
z σy Fig. 1.6
Nomenclatura utilizada
Para las tensiones normales: σx → el subíndice “x”, indica que esta tensión está sobre
una superficie normal al eje X
Para las tensiones cortantes: τxy → el primer subíndice “x”, indica que está sobre una
superficie normal al eje X y el segundo subíndice “y”, indica que lleva la dirección del
eje Y
Observación: en las caras del paralelepípedo paralelas a las que contienen a los ejes
coordenados, las tensiones se las distingue con un “prima” en la parte superior: σ´x, τ´xy
Convenios de signos para las tensiones
Para las tensiones normales: σ → se consideran positivas, (σ > 0), cuando van
dirigidas en el mismo sentido que la normal saliente a la superficie donde está aplicada.
(Si se observa en (Fig. 1.6), todas las tensiones normales dibujadas en las diferentes
caras del paralelepípedo serían positivas).
Para las tensiones cortantes: τ → se consideran positivas, (τ > 0), cuando las que están
aplicadas sobre las caras del paralelepípedo que pasan por O llevan sentido contrario al
de los ejes positivos y las que están aplicadas en las caras que no pasan por O llevan el
mismo sentido que los ejes positivos. (Si se observa en (Fig. 1.6), todas las tensiones
cortantes dibujadas en las diferentes caras del paralelepípedo serían positivas).
5

13. Tema 1: Tensiones
Las tensiones en las tres caras del paralelepípedo que no pasan por O ( σ´x, σ´y, σ´z, τ´xy,
τ´yz, τ´zx ) se podrían expresar matemáticamente en función de las tensiones en las otras
tres caras que pasan por O ( σx, σy, σz, τxy, τyz, τzx ) por desarrollo de Tylor:
∂σ x ∂τ xy ∂τ xz
σ ´x = σ x + .dx τ ´xy = τ xy + .dx τ ´xz = τ xz + .dx
∂x ∂x ∂x
∂σ y ∂τ yx ∂τ yz
σ ´y = σ y + .dy τ ´yx = τ yx + .dy τ ´yz = τ yz + .dy (1.5)
∂y ∂y ∂y
∂σ z ∂τ zx ∂τ zy
σ ´z = σ z + .dz τ ´zx = τ zx + .dz τ ´zy = τ zy + .dz
∂z ∂z ∂z
Si reduciésemos las dimensiones del paralelepípedo, manteniéndose semejante a sí
mismo, el paralelepípedo tendería al punto O y en el límite todas sus caras pasarían por
O, con lo cual se podría considerar que:
σ ´x = σ x τ ´xy = τ xy τ ´xz = τ xz
σ ´y = σ y τ ´yx = τ yx τ ´yz = τ yz (1.6)
σ ´z = σ z τ ´zx = τ zx τ ´zy = τ zy
Así pues, en este caso, serán sólo 9 las tensiones distintas que actúan sobre las caras de
dicho paralelepípedo: 3 tensiones normales y 6 tensiones cortantes.
Por último si establecemos las ecuaciones de equilibrio del paralelepípedo:Σ F = 0,
Σ M = 0, se obtendría que:
τ xy = τ yx τ yz = τ zy τ zx = τ xz (1.7 )
Conclusión: Serán sólo 6 las tensiones distintas que actúan sobre las caras del
paralelepípedo, que serán:
σx σy σz τ xy τ yz τ zx
a estas 6 tensiones se las denomina:Componentes del estado de tensiones del punto O
6

14. Sección 1.3: Estado de tensiones en un punto
TENSOR DE TENSIONES
Supuestamente conocidas las 6 componentes del estado de tensiones en un punto O
cualquiera: σx, σy, σz, τxy, τyz, τzx , vamos a desarrollar una fórmula que permita conocer
las tensiones sobre cualquier superficie que pase por O.
Para ello tracemos una superficie S que cortará al paralelepípedo diferencial en un plano
de área dS y aislemos del cuerpo el elemento de volumen diferencial que en forma de
tetraedro con vértice en O se nos ha formado.
F3
F1
y
dS
F4 O x F5 Fn
F2 z
Fig. 1.7
Ampliando dicho tetraedro y situando las tensiones sobre las caras del mismo será:
y
σz
dS ρ n
τxz τzx τ
σx r r r r
τzy σ siendo en general : ρ = ρ x .i + ρ y . j + ρ z .k
u
τxy x y estando la superficie dS definida por :
O τ r
τyx
yz
u ( cos α , cos β , cos γ )
σy Fig. 1.8
z
Estableciendo las ecuaciones de equilibrio del tetraedro:
∑F x =0 ρ x .ds = σ x .ds.cos α + τ yx .ds.cos β + τ zx .ds.cos γ
dividiendo por ds : ρ x = σ x .cos α + τ yx .cos β + τ zx .cos γ
y haciendo lo mismo en los otros ejes :
∑F x =0 ρ x = σ x .cos α + τ yx .cos β + τ zx .cos γ
∑F y =0 ρ y = τ xy .cos α + σ y .cos β + τ zy .cos γ (1.8)
∑F z =0 ρ z = τ xz .cos α + τ yz .cos β + σ z .cos γ
ecuaciones que expresadas en forma matricial quedará:
7

15. Tema 1: Tensiones
⎡ ρ x ⎤ ⎡σ x τ yx τ zx ⎤ ⎡ cos α ⎤
⎢ ρ ⎥ = ⎢τ ⎥
σ y τ zy ⎥.⎢cos β ⎥
⎢ y ⎥ ⎢ xy ⎢ ⎥ (1.9)
⎢ ρ z ⎥ ⎢τ xz
⎣ ⎦ ⎣ τ yz σ z ⎥ ⎢ cos γ ⎥
⎦⎣ ⎦
r r
y en forma abreviada: ρ = T .u (1.10)
siendo: ⎡σ x τ yx τ zx ⎤
⎢ ⎥
T = ⎢τ xy σ y τ zy ⎥ "Tensor de Tensiones " (1.11)
⎢τ xz τ yz σ z ⎥
⎣ ⎦
Conclusión:
Conocidas las componentes del Estado de Tensiones en un punto: σx, σy, σz, τxy, τyz, τzx
y dada una superficie S cualquiera que pase por dicho punto, definida por su vector
normal unitario: u (cosα, cosβ, cosγ ), se podrá conocer, por la ecuación obtenida (1.9)
la tensión ρ sobre dicha superficie.
Una vez conocida la tensión ρ, se podrá obtener por las ecuaciones (1.2) y (1.3):
rr r r
σ = ρ .u σ = σ .u
r r r (1.12)
τ = ρ −σ τ = ρ 2 −σ 2
Caso Particular: TENSIONES PLANAS:
Se considera que un estado de tensiones es plano cuando se cumpla:
σz = 0, τxz = 0, τyz = 0
(Este es un caso que se presenta con mucha frecuencia)
La ecuación matricial (1.9) sería: ⎡ ρ x ⎤ ⎡σ x τ yx 0⎤ ⎡ cos α ⎤
⎢ ρ ⎥ = ⎢τ σy 0⎥.⎢cos β ⎥
⎢ y ⎥ ⎢ xy ⎥⎢ ⎥
⎢ρ z ⎥ ⎢ 0
⎣ ⎦ ⎣ 0 0⎥ ⎢ cos γ ⎥
⎦⎣ ⎦
o lo que es lo mismo: ⎡ ρ x ⎤ ⎡σ x τ yx ⎤ ⎡cos α ⎤
⎢ ρ ⎥ = ⎢τ .
σ y ⎥ ⎢cos β ⎥
(1.13)
⎣ y⎦ ⎣ xy ⎦⎣ ⎦
ρz = 0
8

16. Sección 1.4: Tensiones Principales
1.4.- TENSIONES PRINCIPALES
De las infinitas Tensiones que puede haber en un punto de un sólido, relativas a las
infinitas superficies S que pasen por él, habrá unas que tengan los valores máximo y
mínimo, a las que se denominará: TENSIONES PRINCIPALES. A las superficies S
correspondientes se las denominará : SUPERFICIES PRINCIPALES y a las
direcciones de los vectores normales a dichas superficies se las denominará:
DIRECCIONES PRINCIPALES.
Para su cálculo se tendrá en cuenta, aunque no se demostrará, que en las Superficies
r r r
Principales se cumplirá: τ = 0 con lo cual : ρ = σ
Existirán pues muchas superficies, como la dS1, (Fig.1.9 a), en las cuales habrá
tensiones normales (σ1) y cortantes (τ1) y habrá algunas, como la dS2, (Fig.1.9 b), en las
que no habrá tensiones cortantes y por tanto sólo habrá tensiones normales (σ2), con lo
cual, en estos casos, la tensión total (ρ2) coincidirá con la tensión normal
F3 F1 F3
F1
y σ1 y
ρ1 ρ2 = σ 2
dS1 u1 dS2 u2
O x F4 O x
F4 τ1 F5 F5
F2 z F2 z τ2 = 0
Fig. 1.9.a Fig. 1.9.b
dS1: Superficie cualquiera dS2: Superficie Principal
CÁLCULO DE LAS TENSIONES PRINCIPALES
Supongamos conocidas las 6 componentes del Estado de Tensiones en un punto O:
σx, σy, σz, τxy, τyz, τzx y sea S una Superficie Principal que pasa por O, definida por su
vector normal unitario: u (cosα, cosβ, cosγ ).
r r
En función de lo dicho antes, se deberá cumplir: ρ = ρ .u con lo cual:
ρ x = ρ . cos α ρ y = ρ . cos β ρ z = ρ . cos γ (1.14)
y llevando estas expresiones a la ecuación (1.8) que da el valor de ρ, quedará:
9

17. Tema 1: Tensiones
ρ x = σ x .cos α + τ yx .cos β + τ zx .cos γ = ( por 1.14) = ρ .cos α
ρ y = τ xy .cos α + σ y .cos β + τ zy .cos γ = ( por 1.14) = ρ .cos β
ρ z = τ xz .cos α + τ yz .cos β + σ z .cos γ = ( por 1.14) = ρ .cos γ
operando:
(σ x − ρ ). cos α + τ yx . cos β + τ zx . cos γ = 0
τ xy . cos α + (σ y − ρ ). cos β + τ zy . cos γ = 0 (1.15)
τ xz . cos α + τ yz . cos β + (σ z − ρ ). cos γ = 0
Y para que este sistema de ecuaciones homogéneo, tenga solución no nula, tendrá que
verificarse que el determinante formado por los coeficientes sea nulo, es decir:
σx −ρ τ yx τ zx
τ xy σy −ρ τ zy = 0 (1.16)
τ xz τ yz σz −ρ
Resolviendo este determinante, que da lugar a una ecuación de tercer grado, se
obtendrán las Tensiones Principales : ρ1, ρ2, ρ3
y se cumplirá: ρ1 = σ1, ρ2 = σ2, ρ3 = σ3
CÁLCULO DE LAS DIRECCIONES PRINCIPALES
Una vez obtenidas las tensiones principales: ρ1, ρ2, ρ3, para conocer las direcciones en
las que éstas aparecen: direcciones principales, se resolverá el sistema de ecuaciones
(1.15) obtenido anteriormente, sustituyendo en él la tensión ρ, para cada uno de los
valores obtenidos de las tensiones principales. Así será:
(σ x − ρ i ). cos α i + τ yx . cos β i + τ zx . cos γ i = 0
τ xy . cos α i + (σ y − ρ i ). cos β i + τ zy . cos γ i = 0 (1.17.a )
τ xz . cos α i + τ yz . cos β i + (σ z − ρ i ). cos γ i = 0
r
y para que la dirección obtenida se exprese como un vector unitario: ui = 1
se auxiliará con la euación:
cos 2 α i + cos 2 β i + cos 2 γ i = 1 (1.17.b)
Las direcciones principales se obtendrán pues resolviendo el sistema de ecuaciones
formado por (1.17.a) y (1.17.b):
para ρ i = ρ1 → cos α1 , cos β1 , cos γ 1
para ρ i = ρ 2 → cos α 2 , cos β 2 , cos γ 2
para ρ i = ρ 3 → cos α 3 , cos β 3 , cos γ 3
10

18. Sección 1.4: Tensiones Principales
CASO PARTICULAR: TENSIONES PLANAS
Para el caso de tensiones planas: σz = 0, τxz = 0, τyz = 0, le ecuación (1.16) que da el
cálculo de las tensiones principales se verá reducida a la ecuación siguiente:
σx −ρ τ yx
=0 (1.18)
τ xy σy −ρ
Resolviendo este determinante, que da lugar a una ecuación de segundo grado, se
obtendrán las Tensiones Principales : ρ1, ρ2
y se cumplirá: ρ1 = σ1, ρ2 = σ2
Desarrollando el determinante: ρ 2 − ρ .(σ x + σ y ) + (σ x .σ y − τ xy ) = 0
2
siendo las raíces de esta ecuación:
(σ x + σ y ) + (σ x + σ y ) 2 − 4.(σ x .σ y − τ xy )
2
ρ1 =
2
(σ x + σ y ) − (σ x + σ y ) 2 − 4.(σ x .σ y − τ xy )
2
ρ2 =
2
y operando:
σx +σ y 1
ρ1 = σ 1 = + . (σ x − σ y ) 2 + 4 .τ xy
2
2 2
(1.19)
σx +σ y 1
ρ2 = σ 2 = − . (σ x − σ y ) 2 + 4.τ xy
2
2 2
Por su parte las direcciones principales se obtendrán a partir de las ecuaciones (1.17.a) y
(1.17.b) eliminando los términos representativos de la tercera dimensión y se verán
reducidas a las expresiones:
(σ x − ρ i ). cos α i + τ yx . cos β i = 0
(1.20.a )
τ xy . cos α i + (σ y − ρ i ). cos β i + = 0
cos 2 α i + cos 2 β i = 1 (1.20.b)
Las direcciones principales se obtendrán pues resolviendo el sistema de ecuaciones
formado por (1.20.a) y (1.20.b):
para ρ i = ρ1 → cos α1 , cos β1
para ρ i = ρ 2 → cos α 2 , cos β 2
11

19. Tema 1: Tensiones
1.5.- REPRESENTACIÓN DE MOHR
En los apartados anteriores se ha visto un método de cálculo analítico para el cálculo de
Tensiones. En este apartado se verá un método gráfico.
CASO PARTICULAR: TENSIONES PLANAS
El método gráfico se va a desarrollar en primer lugar para el caso de Tensiones Planas,
pues es el que mas se utilizará debido a su sencillez de aplicación y la gran ayuda de su
aportación gráfica.
Supongamos conocidas las tres componentes del estado de tensiones plano en un punto
O: σx, σy, τxy (Fig.1.10 a). Al no existir tensiones en la tercera dimensión (z), se podrá
simplificar el dibujo y representar tan sólo la proyección del ele mento diferencial de
volumen sobre el plano xy. (Fig.1.10 b)
y σy
y σy
τyx
τyx
τxy σ
σx σx S u τxy
σx α σx
τxy O τxy τ
x
τyx O τ x
z yx
σy σy
Fig.1.10.a Fig.1.10.b
Se desea conocer las tensiones correspondientes a una superficie S cualquiera, que
pasa por O y definida por su vector normal unitario:u (cosα, cosβ, 0).
Empleando las ecuaciones analíticas (1.13) y (1.12) para cada superficie S se obtendrán
los valores de las tensiones σ y τ correspondientes. Así:
para α = α1 → superficie S1 → σ 1 ,τ 1
para α = α 2 → superficie S 2 → σ 2 ,τ 2
.............................................................................
para α = α n → superficie S n → σ n ,τ n
Si representásemos estos valores obtenidos en unos ejes coordenados, en los que en el
eje de abcisas llevásemos las tensiones normales y en el de ordenadas, las cortantes y
uniésemos todos ellos, se demuestra, no lo haremos, que el lugar geométrico de los
mismos es una circunferencia, a la que denominaremos “Circunferencia de Mohr”
τ (σ2,τ2)
(σ1,τ1)
O σ
(σn,τn) Fig.1.11
12

20. Sección 1.5: Representación de Mohr
Se demuestra, aunque no se hará, que la circunferencia de Mohr obtenida al unir todos
los puntos: (σ1τ1), (σ2τ2),…… (σnτn), es una circunferencia que tiene por Centro y
Radio los siguientes valores:
2
⎛σ +σ y ⎞ ⎛ σ −σ y ⎞ (1.21)
⎟ + τ xy
2
Centro : ⎜ x ,0⎟ Radio : ⎜ x
⎝ 2 ⎠ ⎝ 2 ⎠
siendo: σx, σy, τxy, las tres componentes del estado de tensiones planas en el punto O.
Criterios de signos para las tensiones, al utilizar el método gráfico de Mohr
• Tensiones normales (σ): se consideran positivas las tensiones normales cuyo
sentido es saliente de la superficie, es decir en el sentido de la normal exterior a
la superficie. Negativas en caso contrario
σ<0
σ>0 S
S
next next
Fig.1.12.a Fig.1.12.b
• Tensiones cortantes (τ): se consideran positivas cuando su sentido deja a la
derecha a la superficie. Dicho de otro modo, cuando su sentido de circulación
(en sentido figurado), alrededor del elemento es horario. En la (Fig. 1.13.a) se
representan las diferentes posiciones de τ > 0, con respecto a la superficie S.
Las posiciones de τ < 0, caso contrario, se indican en la (Fig.1.13.b)
τ τ
τ τ τ τ
S S
S S S S
τ S τ>0 S τ τ S τ<0 S τ
S S S S
S τ S τ
τ τ
τ τ
Fig.1.13.a Fig.1.13.b
Observación: Los criterios de signos utilizados para las tensiones cortantes, en la
representación gráfica de Mohr, no coinciden con los dados en 1.3. para la resolución
analítica. Este hecho habrá de tenerse siempre en cuenta en la resolución de los
problemas.
13

21. Tema 1: Tensiones
Construcción de la circunferencia de Mohr:
Supónganse conocidas las componentes del estado de tensiones plano en un punto O:
σx, σy, τxy (Fig.1.14.a) y tracemos unos ejes coordenados en donde en el eje de abcisas
llevaremos las tensiones normales (σ) y en el de ordenadas las tensiones cortantes (τ).
(Fig.1.14.b).
La construcción de la Circunferencia de Mohr relativa a dicho estado de tensiones se
hará de la siguiente forma:
La superficie SA ( σx>0, τxy<0, por criterios de signos de Mohr), vendrá representada en
los ejes coordenados por el punto A. A su vez, la superficie SB ( σy>0, τyx>0, por
criterios de signos de Mohr), vendrá representada en los ejes coordenados por el punto
B. Si unimos, con una recta, los puntos A y B, la intersección de ésta con el eje de
abcisas (punto C), será el centro de la circunferencia de Mohr. (Fig.1.14.b)
y σy
τ
τyx
B
SB
τxy
σx τyx
SA SA σx σy σx
τxy O E C D σ
SB τxy
O x
τyx A
σy
Fig.1.14.a Fig.1.14.b
OD + OE σ x + σ y
Efectivamente con la construcción realizada, el centro será: OC = =
2 2
2
⎛σ x −σ y ⎞
y el radio será: CA = (CD ) + (DA )
2 2
= ⎜
⎜ ⎟ + τ xy
⎟
2
⎝ 2 ⎠
expresiones que coinciden con las expresadas anteriormente en (1.21).
14

22. Sección 1.5: Representación de Mohr
Cálculo de las tensiones σ y τ en una superficie S cualquiera:
A partir de las componentes del estado de tensiones plano en un punto O: σx, σy, τxy, se
dibujará en un sistema de ejes coordenados: (σ, τ), la circunferencia de Mohr tal y como
se ha indicado en el apartado anterior, obteniendo su centro y su radio
Indiquemos a continuación cómo poder conocer gráficamente las tensiones σ y τ
correspondientes a una superficie S cualquiera que pase por O, definida por su vector
normal unitario: us (cosα, cosβ, 0).(Ver Fig.1.15.a)
β
y σy
τ S
τyx
β 2α
B
SB α
σ τxy τ
S τyx
σx
uS τ SA uA σx σ σx
O σy C H D σ
τxy τxy
O x
τyx A
σy
Fig.1.15.a Fig.1.15.b
El procedimiento será el siguiente: Para pasar de la superficie SA (definida por uA), a la
superficie S (definida por uS), se deberá girar, en sentido antihorario, el ángulo α. Pues
bien, para pasar en la circunferencia de Mohr, del punto A, (representativo del estado de
tensiones de la superficie SA), al punto S, (que representará el estado de tensiones de la
superficie S), se tendrá que girar, igualmente en sentido antihorario, el ángulo 2α (“ el
doble del anterior ”). (Ver Fig.1.15.b)
Mediante este procedimiento las tensiones en la superficie S serán pues:
tensión normal: σ = OH = OC + CH = OC + CS .cos β
tensión cortante: τ = SH = CS .sen β
(los valores de OC “centro” y CS “radio” se han obtenido anteriormente de la
circunferencia de Mohr)
Observación:
Como consecuencia del procedimiento anterior resultará, que dos superficies
perpendiculares que pasen por O, estarán representadas gráficamente en la
circunferencia de Mohr por dos puntos diametralmente opuestos de dicha
circunferencia. Véase por ejemplo el caso de las superficies SA y SB representadas en
los puntos diametralmente opuestos A y B de la circunferencia de Mohr. (Fig.1.15.a y
1.15.b)
15

23. Tema 1: Tensiones
Cálculo de las tensiones principales:
Se sabe, por lo visto en (1.4) que las tensiones principales son las tensiones máxima y
mínima y que en las superficies donde aparecen, no hay tensiones cortantes. Es decir, se
cumple: ρ =σ, τ = 0.
y
90º
σy τ
SB τyx B
σ1=σmax
σ2=σmin τyx
σx uM ϕ1 σ2 σx M
SN
uA σx O N σy C D σ1 σ
τxy SM τxy τxy
SA 2ϕ1
O x A
τyx
σy
Fig.1.16.a Fig.1.16.b
De la circunferencia de Mohr, (Fig.1.16.b), se observa que los puntos M y N de dicha
circunferencia cumplen dichas condiciones. Así pues las tensiones principales serán:
2
σx +σ y ⎛σ x −σ y ⎞
σ 1 = ρ1 = σ max = OM = OC + C M = C entro + Radio = + ⎜ ⎟ + τ xy
2
2 ⎝ 2 ⎠
2
σx +σ y ⎛σx −σ y ⎞
σ 2 = ρ 2 = σ min = ON = OC − CN = Centro − Radio = − ⎜ ⎟ + τ xy
2
2 ⎝ 2 ⎠
(1.22)
(son las mismas ecuaciones (1.19) obtenidas analíticamente)
Las direcciones principales también se podrán obtener a partir de la circunferencia de
Mohr. Se observa (Fig.1.16.b), para pasar del punto A del circulo (representativo del
estado de tensiones de la superficie SA), al punto M, que es donde se dará la tensión
principal: σ1 = σmax, hay que girar en sentido antihorario el ángulo 2ϕ1. Así pues para
obtener la superficie principal: SM, sobre la que se dará dicha tensión principal, se
deberá girar la Superficie SA, en el mismo sentido (es decir antihorario), el ángulo ϕ1.
(Fig.1.16.a).
AD τ xy
tag 2ϕ1 = = ⇒ ϕ1
siendo: CA σ x − σ y (1.23)
2
La otra dirección principal, la correspondiente al punto N, donde se dará la tensión
principal mínima: σ2 = σmin, se obtendrá girando la anteriormente hallada otros 90º. (ver
Fig.1.16.a), es decir en la dirección: ϕ2 = ϕ1 ± 90º (los puntos M y N están a 180º en la
circunferencia).
16

24. Sección 1.5: Representación de Mohr
Cálculo de la tensión cortante máxima:
Los puntos del círculo de Mohr donde la tensión cortante es máxima, son los puntos F y
G, los de máxima ordenada. (Fig.1.17).
τ F
B
τmax
τyx
σ2 σx M
O N σy C D σ1 σ
τxy
2ϕ1
τmax
A
G
Fig.1.17
El valor de la tensión cortante máxima será pues:
2
⎛σ x −σ y ⎞
τ max = CF = Radio = ( por ecuación 1.21) = ⎜ ⎟ + τ xy
2
(1 .24)
⎝ 2 ⎠
o bien:
Diámetro OM − ON σ 1 − σ 2
τ max = Radio = = = (1.25)
2 2 2
Las superficies SF y SG, donde se darán las τmax, estarán a ± 45º de las superficies
principales SM y SN, pues los puntos F y G de la circunferencia se encuentran a 90º de
los puntos M y N. (Fig.1.17).
CASO DE TENSIONES TRIAXIALES
Se dice que un elemento de material se encuentra en un estado de tensiones triaxial
cuando está sometido a tensiones en los tres ejes coordenados.
Supongamos un punto O, un paralelepípedo diferencial alrededor de él y sean los ejes 1,
2 y 3, los ejes principales
2
σ2
σ3 σ1
σ1
σ3
O 1
3 σ2 Fig.1.18
17

25. Tema 1: Tensiones
Si se corta por una superficie inclinada S, paralela al eje 3, las tensiones σ y τ sobre
dicha superficie las podremos obtener del círculo de Mohr (A), (ver fig. 1.20),
correspondiente a las tensiones σ1 y σ2, similar a un estado de tensiones plano (pues las
tensiones σ3 no afectarían a dicha superficie).
2 nS
σ
θ
S
τ
σ1 σ3
σ3 O
1
3 σ2
Fig.1.19
La misma conclusión general es válida si cortásemos por una superficie S paralela al eje
2 (en este caso las tensiones σ y τ sobre dicha superficie las podríamos obtener del
círculo de Mohr (B), (ver fig.1.20), correspondiente a las tensiones σ1 y σ3, similar a un
estado de tensiones plano (pues las tensiones σ2 no afectarían a dicha superficie) o si
cortásemos por una superficie S paralela al eje 1 (en este caso las tensiones σ y τ sobre
dicha superficie las podríamos obtener del círculo de Mohr (C), (ver fig.1.20),
correspondiente a las tensiones σ2 y σ3).
Se ha supuesto en la construcción de los círculos que: σ1 > σ2 > σ3
B
τ
τMAX A
C
τ
O
O σ3 σ2 σ1 σ
Fig.1.20
En cada uno de los círculos podremos hallar la τmax correspondiente, siendo la τMAX
absoluta la correspondiente al círculo de Mohr mayor (B) y valdría:
σ −σ3
τ MAX = 1
2
En el análisis anterior hemos considerado el cálculo de las tensiones σ y τ sobre
superficies S paralelas a uno de los ejes principales. Si se quisieran calcular sobre otras
superficies S cualquiera, (no paralelas a ningún eje principal), el análisis sería algo más
complejo y no se verá en este apartado, aunque se sabe que los valores correspondientes
de σ y τ darán puntos situados sobre el área limitada por las tres circunferencias de
Mohr
18

26. Sección 1.6: Formas de trabajo de una sección. Relaciones entre tensiones y solicitaciones
1.6.- FORMAS DE TRABAJO DE UNA SECCIÓN. RELACIONES ENTRE
TENSIONES Y SOLICITACIONES
FORMAS DE TRABAJO DE UNA SECCIÓN
Consideremos un sólido sometido a un sistema de fuerzas exteriores y que se encuentra
en equilibrio estático y elástico.
F1 F3
S Fn
F4 F5
F2
Fig. 1.21.a
Según lo visto en el apartado 1.1, si se desea conocer las Fuerzas Internas o Tensiones
que aparecen en una superficie determinada S, seccionamos el sólido por dicha
superficie y nos quedamos con una de las dos partes del mismo
F1
S
∆F
F4 O
∆S
F2
Fig. 1.21.b
El trozo de sólido seccionado no estará en equilibrio, a no ser que se restablezcan las
acciones que el otro trozo ejercía sobre él. Estas acciones son precisamente las Fuerzas
Internas o Tensiones que aparecerían sobre los puntos de la superficie S seccionada.
Pues bien, para saber algo de ellas, hagamos lo siguiente:
F1
S z
G x
F4
F2
y Fig. 1.21.c
Tomemos un sistema de ejes coordenados con origen en G (centro de gravedad de la
sección S), siendo el eje X perpendicular a la superficie S y con sentido positivo saliente
de la misma y los ejes Y y Z los ejes principales de la sección S, con sus sentidos
positivos de tal forma que formen un triedro directo
19

27. Tema 1: Tensiones
La acción de las Fuerzas Exteriores, actuando sobre este trozo del sólido, en el punto G,
vendrán dadas por: Rext y Mext
F1 Rext Mext
S z
Rext = Resultante de las Fuerzas Exteriores
G x Mext = Momento resultante de las Fuerzas
F4 Exteriores respecto de G
F2
y
Fig. 1.21.d
Para que este trozo de sólido seccionado esté en equilibrio, el sistema de Fuerzas
Interiores extendido a lo largo de la superficie S, (fuerzas que las partículas del otro
lado de la superficie S que hemos apartado, estaban actuando sobre las partículas de la
superficie S del lado del sólido que nos hemos quedado), producirán una acción en G
dada por: Rint y Mint y se tendrá que cumplir que:
Rint = - Rext
Mint = - Mext
F1 Rext Mext
S z
G x
F4
F2
Mint Rint
y
Fig. 1.21.e
Por último, si proyectamos Rint y Mint sobre los tres ejes de referencia XYZ, nos darán 6
componentes: Rx, Ry, Rz, Mx, My, Mz,
F1
z
S Rz
Mz Rx
G x
F4 Mx
My
F2
Mint Ry
Rint
y
Fig. 1.21.f
20

28. Sección 1.6: Formas de trabajo de una sección. Relaciones entre tensiones y solicitaciones
Cada una de esas componentes nos indica una Forma de Trabajo o de Solicitación de la
sección S:
Rx (fuerza normal) → N (TRACCIÓN – COMPRESIÓN)
Ry (fuerza cortante) → Vy (CORTADURA en eje Y)
Rz (fuerza cortante) → Vz (CORTADURA en eje Z)
Mx (momento torsor) → T (TORSIÓN)
My (momento flector) → My (FLEXIÓN en plano XZ, alrededor del eje Y)
Mz (momento flector) → Mz (FLEXIÓN en plano XY, alrededor del eje Z)
Ejemplos:
F1 TRACCIÓN COMPRESIÓN
S
z N F F F F
F4
G x x x
F2
y
CORTADURA en eje Y
F1
S F
z
G x
F4 x
F2
Vy y
y
F1 z CORTADURA en eje Z
Vz
S
z
G x
F4
x
F2
y
y F
TORSIÓN
F1 M
S
z
G x
F4
T x
F2
y
FLEXIÓN en plano XZ
F1 (alrededor eje y)
S
z z
G x
F4
F2
x
My
y
y F
FLEXIÓN en el plano XY
F1 (alrededor eje Z)
Mz
S
z
F
G x
F4
F2 x
y
Fig.1.22 y
21

29. Tema 1: Tensiones
RELACIONES ENTRE TENSIONES Y SOLICITACIONES
Cada una de estas Solicitaciones así obtenidas serán resultado de las Tensiones (o
Fuerzas Internas) distribuidas a lo largo de la sección S. Unas y otras estarán
relacionadas de la siguiente manera:
F1 Sección S
Vz z
S
Mz T N
G x G
F4 dS σ
My y z
τ ρ z τxz
F2
Vy
τxy τ
y
y
Fig. 1.23.a Fig.1.23.b
N = ∫ σ x .dS V y = ∫ τ xy .dS V z = ∫ τ xz .dS
S S S
(1.26)
T = ∫ (τ
S
xz . y − τ xy .z ).dS M y = ∫ σ x .z.dS
S
M z = ∫ σ x . y.dS
S
Estas ecuaciones se utilizarán para calcular las Tensiones o Fuerzas internas en cada
uno de los puntos de una sección S, una vez conocidas las Solicitaciones (Resultante y
Momento resultante de las Fuerzas interiores: N, Vy, Vz, T, My, Mz) .
22

30. Tema 2: Deformaciones
Tema 2 : DEFORMACIONES
F1 F3
γ1/2
γ2/2 ε2 ε1
u1 δ1
δ2 u2
u3 δ3
O
ε3 γ3/2
F2
Fn
1

31. Tema 2: Deformaciones
2.1.- INTRODUCCIÓN
Los cuerpos se deforman debido a la acción de las fuerzas aplicadas. Para conocer la
deformación de un cuerpo es preciso conocer primero la deformación de uno cualquiera
de los paralelepípedos elementales que lo forman.
Veremos a continuación cómo la deformación de un paralelepípedo elemental se puede
descomponer e cuatro partes:
1º.- Una TRASLACIÓN que lleva el origen del paralelepípedo del punto O al punto O´
F3
F1
y
O x Fn
F4 O´ F5
F2 z
Fig. 2.1
2º.-Una ROTACIÓN del paralelepípedo alrededor de un eje que pasa por O´
F3
F1 Eje Rotación
F4 O´ F5 Fn
F2
Fig. 2.2
Estas dos primeras partes van a originar el movimiento del paralelepípedo, pero sin
deformarse
2

32. Sección 2.1: Introducción
3º.-Unas DEFORMACIONES LINEALES de las aristas del paralelepípedo
F3
F1
F4 O´ F5 Fn
F2
Fig. 2.3
4º.- Unas DEFORMACIONES ANGULARES “SIMÉTRICAS” de los ángulos que
forman las aristas del paralelepípedo, inicialmente a 90º.
F3
F1
F4 O´ F5 Fn
F2
Fig. 2.4
Estas dos últimas partes son las que originan la deformación propiamente dicha del
paralelepípedo.
Observación:
En la 4ª parte nos hemos referido a Deformaciones Angulares “Simétricas”. El por qué
de ello lo veremos a continuación:
Supongamos la cara del paralelepípedo contenida en el plano XOY y supongamos, por
ejemplo, que la arista OA gira 4º en sentido antihorario y la arista OB gira 2º en sentido
horario. Estas deformaciones angulares las podemos obtener como suma de dos
acciones: en una primera acción hacemos girar las aristas el mismo ángulo, lo que
denominaremos deformación angular simétrica, que sería la media aritmética de las dos,
o sea: 3º y en la segunda acción completamos la deformación angular inicial, con lo cual
la arista OA habría que girarla 1º mas en sentido antihorario y la arista OB restarla 1º,
osea, girarla 1º en sentido horario. Ésta acción sería una rotación
2º 3º 1º
B deformación B deformación B rotación
angular angular simétrica
= +
4º 3º 1º
O A O A O A
3

33. Tema 2: Deformaciones
2.2.- CONCEPTO DE DEFORMACIÓN
Como consecuencia de la deformación propiamente dicha del paralelepípedo:
deformaciones lineales y deformaciones angulares simétricas, el vértice D del
paralelepípedo experimentará el desplazamiento DD´, con lo cual el elemento lineal
OD, modifica su longitud y gira un ángulo transformándose en el elemento lineal OD´.
y
D
D´
Do δ
1 Do´
O
x
z
Fig. 2.5
Definición: Se denomina DEFORMACIÓN UNITARIA (δ) del elemento lineal OD, al
cociente entre el desplazamiento sufrido por su extremo: DD´ y la longitud del elemento
lineal: OD, es decir:
r DD´
δ = (2.1)
OD
Si observamos la fig.2.5. se ve que δ es el desplazamiento que sufre el vector unitario
ODo en la dirección del elemento lineal OD. En efecto, por semejanza de triángulos
ODD´y ODoDo´ se obtiene:
δ DD´ DD´
= → δ=
1 OD OD
Descompondremos a continuación el vector δ en dos componentes: una sobre la propia
dirección del elemento lineal OD, a la que denominaremos: DEFORMACIÓN
LONGITUDINAL UNITARIA (ε) y otra en dirección perpendicular al elemento lineal
OD, a la que denominaremos: DEFORMACIÓN ANGULAR UNITARIA (γ/2). Se
cumplirá:
y
D r
D´ r r γ
δ =ε +
γ/2 2
Doε (2.2)
1 δ Do´ ⎛γ ⎞
2
δ = ε2 +⎜ ⎟
x ⎝2⎠
O
z
Fig. 2.6
4

34. Sección 2.2: Concepto de deformación
2.3.- ESTADO DE DEFORMACIONES EN UN PUNTO
Como se verá a continuación, va a existir una analogía entre el Estado de Tensiones y el
Estado de Deformaciones
Tal y como se vió en 1.3 que……………..”a cada superficie S que pase por un punto O
de un sólido le corresponde una tensión ρ, con componentes: σ (tensión normal) y τ
(tensión cortante)”……………..y “al conjunto de todas las tensiones que pueda haber
en un punto O se las denomina: Estado de Tensiones del punto O”
En el caso de las deformaciones va a ocurrir algo similar:
“A cada elemento lineal que pasa por un punto O de un sólido le corresponde una
deformación unitaria δ, con componentes: ε (deformación longitudinal unitaria) y γ/2
(deformación angular unitaria).”
F1 F3
γ1/2
γ2/2 ε2 ε1
u1 δ1
δ2 u2
u3 δ3
O
ε3 γ3/2
F2
Fn
Fig. 2.7
“Al conjunto de todas las deformaciones que pueda haber en el punto O sw le
denomina: Estado de Deformaciones del puno O”
Siguiendo con dicha analogía, vimos en 1.3 que…………….”de las infinitas Tensiones
que puede haber en un punto O correspondientes a las infinitas superficies que pasan
por él, conocidas 6 de ellas: σx, σy, σz, τxy, τyz, τzx, denominadas componentes del
estado de tensiones en el punto O, podremos conocer todas las demás a través de la
ecuación (1.9):
⎡ ρ x ⎤ ⎡σ x τ yx τ zx ⎤ ⎡ cos α ⎤
⎢ ρ ⎥ = ⎢τ ⎥⎢ ⎥
⎢ y ⎥ ⎢ xy σ y τ zy ⎥.⎢cos β ⎥
⎢ ρ z ⎥ ⎢τ xz τ yz σ z ⎥ ⎢ cos γ ⎥
⎣ ⎦ ⎣ ⎦⎣ ⎦
Pues bien, en el caso de las Deformaciones ocurrirá algo similar y así podremos decir:
“De las infinitas Deformaciones que puede haber en un punto O, correspondientes a las
infinitas direcciones de elementos lineales que puedan pasan por él, conocidas 6 de
ellas: εx, εy, εz, γxy, γyz, γzx, denominadas componentes del estado de deformaciones en el
punto O, podremos conocer todas las demás, a través de una ecuación matricial, que
como ahora se verá, será similar a la de las tensiones (1.9).”
5

35. Tema 2: Deformaciones
Sea un punto O del interior de un sólido en el que se suponen conocidas las 6
componentes del estado de deformaciones: εx, εy, εz, γxy, γyz, γzx y sea OD un elemento
lineal cuya deformación unitaria δ se desea conocer.
La dirección del elemento lineal OD la definiremos por su vector unitario: u = ODo ,
dado por sus cosenos directores: u (cos α, cos β, cos γ). Construyamos ahora un
paralelepípedo con diagonal entre vértices opuestos ODo = 1 (ver fig.2.8). El
paralelepípedo así construido tendrá por aristas: cos α (en dirección del eje OX), cos β
(en dirección del eje OY) y cos γ (en dirección del eje OZ).
y
D
D´
Do
δ
cos β
1 Do´
u
O cos α x
cos γ
z
Fig. 2.8
Para obtener el valor de la deformación unitaria δ calcularemos y sumaremos los
correspondientes desplazamientos sufridos por el punto Do debidos a las deformaciones
longitudinales y angulares unitarias dadas, correspondientes al punto O: εx, εy, εz, γxy,
γyz, γzx.
• Desplazamiento δ debido a las deformaciones longitudinales: εx, εy, εz,
y
εy.cosβ
δ
cos β
cos α εx.cosα
O x
cos γ
εz.cosγ
z
Fig. 2.9
δ x = ε x . cos α δ y = ε y . cos β δ z = ε z . cos γ
6

36. Sección 2.3: Estado de deformaciones en un punto
• Desplazamiento δ debido a las deformaciones angulares: γxy, γyz, γzx.
y (γyx/2).cosβ
δ
γyx/2 γ yx
δx = . cos β
2
cos β (γxy/2).cosα
γ xy
δy = . cos α
2
γxy/2
O cos α x
O cos α
γxz/2 x
γ zx
cos γ (γxz/2).cosα δx = . cos γ
2
γ xz
γzx/2 δz = . cos α
2
δ
z
(γzx/2).cosγ
(γyz/2).cosβ
y
δ
γ zy
δy = . cos γ
γyz/2 2
(γzy/2).cosγ γ yz
cos β δz = . cos β
2
γzy/2
O
z cos γ
Fig. 2.10.a), b), c)
Sumando finalmente todos los desplazamientos δ obtenidos quedaría:
γ yx γ zx
δ x = ε x . cos α + . cos β + . cos γ
2 2
γ xy γ zy (2.3)
δy = . cos α + ε y . cos β + . cos γ
2 2
γ xz γ yz
δz = . cos α + . cos β + ε z . cos γ
2 2
7

37. Tema 2: Deformaciones
Poniendo las ecuaciones (2.3) en forma matricial, sería:
⎡ γ yx γ zx ⎤
⎢ εx ⎥
⎡δ x ⎤ ⎢ 2 2 ⎥ ⎡cos α ⎤
⎢δ ⎥ = ⎢ γ xy εy
γ zy ⎥ ⎢
.⎢cos β ⎥ (2.4)
⎢ y⎥ ⎢ 2 2 ⎥ ⎥
⎢δ z ⎥ ⎢ γ
⎣ ⎦ γ yz ⎥⎣⎢ cos γ ⎥
⎦
⎢
xz
εz ⎥
⎣ 2 2 ⎦
r r
y en forma abreviada: δ = D.u (2.5)
siendo: γ yx γ zx
εx
2 2
γ xy γ zy
D= εy "Tensor de Deformaciones"
2 2
γ xz γ yz
εz
2 2
Conclusión:
Conocidas las componentes del Estado de Deformaciones en un punto O: εx, εy, εz, γxy,
γyz, γzx y dada una dirección OD cualquiera, definida por su vector unitario:
u (cosα, cosβ, cosγ ), se podrá conocer, por la ecuación obtenida (2.4), la deformación δ
en dicha dirección.
Una vez conocida la deformación δ, se podrá obtener ε y γ/2, (ver fig.2.6):
rr r r
ε = δ .u ε = ε .u
r r (2.6)
γ r γ
=δ −ε = δ 2 −ε 2
2 2
CASO PARTICULAR: DEFORMACIONES PLANAS
Se considera un estado de deformaciones planas cuando se cumpla:
ε z = 0, γ xz = 0, γ yz = 0
La ecuación matricial (2.4) se verá reducida a:
⎡ γ yx ⎤
⎡δ x ⎤ ⎢ ε x ⎥
2 ⎥.⎡ cos α ⎤
⎢δ ⎥ = ⎢ γ ⎢cos β ⎥ (2.7)
⎣ y ⎦ ⎢ xy εy ⎥ ⎣ ⎦
⎢ 2
⎣ ⎥
⎦
8

38. Sección 2.3: Estado de deformaciones en un punto
Convenios de signos para las deformaciones
Para las deformaciones longitudinales: ε → se consideran positivas, (ε > 0), cuando
expresen alargamientos (negativas en caso contrario)
D D
ε>0 ε<0
1 Do´
Do 1 Do
O Do´
O
Fig. 2.11
el vector unitario ODo, en la dirección OD, el vector unitario ODo, en la dirección OD,
se alarga y pasa a ODo´ se acorta y pasa a ODo´
Para las deformaciones angulares: γ → se consideran positivas, (γ > 0), cuando
indiquen una disminución del ángulo recto inicial que forman las aristas del
paralelepípedo que están en los ejes coordenados (negativas en caso contrario)
y γyx/2 y
γ /2
B yx B´ B´ B
γxy > 0 γxy < 0
A´
γxy/2 A
O A x O γxy/2 x
A´
Fig. 2.12
Lo mismo sería con γxz y γyz
Observaciones: Analogías entre el Estado de Tensiones y el Estado de
deformaciones
Vistas las analogías entre el Estado de Tensiones y el Estado de Deformaciones, se
podrá concluir que si se en todas las ecuaciones obtenidas en el Tema 1 sobre
Tensiones, se hacen los siguientes cambios:
r r r r r γ
ρ → δ σ → ε τ →
2
se obtendrán las ecuaciones equivalentes correspondientes al Tema 2 sobre
Deformaciones.
En efecto:
9

39. Tema 2: Deformaciones
TENSIONES DEFORMACIONES
⎡ γ yx γ zx ⎤
⎢ εx ⎥
⎡ ρ x ⎤ ⎡σ x τ yx τ zx ⎤ ⎡ cos α ⎤ ⎡δ x ⎤ ⎢ 2 2 ⎥ ⎡cos α ⎤
⎢ ρ ⎥ = ⎢τ ⎥ ⎢δ ⎥ = ⎢ γ xy γ zy ⎥ ⎢
.⎢cos β ⎥ (2.4)
⎢ y ⎥ ⎢ xy σ y τ zy ⎥.⎢cos β ⎥ (1.9) ⎢ y⎥ ⎢ 2 εy ⎥
⎢ ⎥ 2 ⎥
⎢ ρ z ⎥ ⎢τ xz
⎣ ⎦ ⎣ τ yz σ z ⎥ ⎢ cos γ ⎥ ⎢δ z ⎥ ⎢ γ
⎣ ⎦ γ yz ⎥⎣⎢ cos γ ⎥
⎦
⎦⎣ ⎦
εz ⎥
⎢
xz
⎣ 2 2 ⎦
rr r r rr r r
σ = ρ .u σ = σ .u ε = δ .u ε = ε .u
(1.12) r r (2.6)
r r r γ r γ
τ = ρ −σ τ = ρ 2 −σ 2 =δ −ε = δ 2 −ε 2
2 2
2.4.- DEFORMACIONES PRINCIPALES
De las infinitas Deformaciones que puede haber en un punto O de un sólido, relativas a
las infinitas direcciones OD que se puedan considerar, habrá unas que tengan los
valores máximo y mínimo a las que se denominará: DEFORMACIONES
PRINCIPALES. A las direcciones correspondientes en la que eso ocurre, se las
denominará : DIRECCIONES PRINCIPALES.
Ocurrirá pues igual que con las tensiones, que en las direcciones principales se cumplirá
que: γ / 2 = 0 y por tanto: δ = ε.
F3 F3
F2 F2
y D y D
Do ε γ/2 Doε = δ
1 1
δ
O x z O x
z γ/2 = 0
Fn Fn
F1 F1
OD: dirección OD: dirección
cualquiera principal
Fig. 2.13
10

40. Sección 2.4: Deformaciones Principales
CÁLCULO DE LAS DEFORMACIONES PRINCIPALES
En el tema de Tensiones las ecuaciones 1.16, nos permitían calcular las tensiones
principales:
σx −ρ τ yx τ zx ρ1 = σ 1
τ xy σy −ρ τ zy = 0 → ρ2 = σ 2
τ xz τ yz σz −ρ ρ3 = σ 3
Las ecuaciones correspondientes para calcular las Deformaciones Principales, se
obtendrán, por lo dicho antes, haciendo los cambios:
r r r r r γ
ρ → δ σ → ε τ →
2
y quedarán las ecuaciones:
γ yx γ zx
εx −δ
2 2
γ xy γ zy
ε y −δ =0 (2.8)
2 2
γ xz γ yz
εz −δ
2 2
Resolviendo este determinante, que da lugar a una ecuación de tercer grado, se
obtendrán las Deformaciones Principales : δ1, δ2, δ3
y se cumplirá: δ1 = ε1, δ2 = ε2, δ3 = ε3
CÁLCULO DE LAS DIRECCIONES PRINCIPALES
En el tema 1 relativo a las tensiones, el cálculo de las Direcciones Principales venían
dadas por las ecuaciones 1.17.a y b.:
(σ x − ρ i ). cos α i + τ yx . cos β i + τ zx . cos γ i = 0
τ xy . cos α i + (σ y − ρ i ). cos β i + τ zy . cos γ i = 0
τ xz . cos α i + τ yz . cos β i + (σ z − ρ i ). cos γ i = 0
cos 2 α i + cos 2 β i + cos 2 γ i = 1
Pues bien, haciendo nuevamente los cambios:
r r r r r γ
ρ → δ σ → ε τ →
2
11

41. Tema 2: Deformaciones
obtendremos las Direcciones Principales correspondientes a las Deformaciones
Principales y serán:
γ yx γ zx
(ε x − δ i ). cos α i + . cos β i + . cos γ i = 0
2 2
γ xy γ zy (2.9.a)
. cos α i + (ε y − δ i ). cos β i + . cos γ i = 0
2 2
γ xz γ yz
. cos α i + . cos β i + (ε z − δ i ). cos γ i = 0
2 2
cos 2 α i + cos 2 β i + cos 2 γ i = 1 (2.9.b)
CASO PARTICULAR: DEFORMACIONES PLANAS
Para el caso particular de deformaciones planas: ε z = 0, γ xz = 0, γ yz = 0
,
La ecuación para el cálculo de las Deformaciones Principales (2.8) quedaría reducida a
:
γ yx
εx −δ
2 =0 (2.10)
γ xy
ε y −δ
2
Resolviendo este determinante, que da lugar a una ecuación de segundo grado se
tendrán las Deformaciones Principales : δ1, δ2
y se cumplirá: δ1 = ε1, δ2 = ε2
Si aplicamos la fórmula de resolución de la ecuación de 2º grado, se obtendrían:
2
εx +εy ⎛ γ xy ⎞
+ . (ε x − ε y ) + 4.⎜
1
δ1 = ε 1 = 2
⎜ 2 ⎟
⎟
2 2 ⎝ ⎠ (2.11)
2
εx +εy ⎛γ ⎞
− . (ε x − ε y ) + 4.⎜ xy
1
δ2 = ε2 = 2
⎜ 2 ⎟
⎟
2 2 ⎝ ⎠
Por
su parte las Direcciones Principales se obtendrán de:
γ yx
(ε x − δ i ). cos α i + . cos β i = 0
2 (2.12.a)
γ xy
. cos α i + (ε y − δ i ). cos β i = 0
2
cos 2 α i + cos 2 β i = 1 (2.12.b)
12

42. Sección 2.5: Representación de Mohr
2.5.- REPRESENTACIÓN DE MOHR
Al igual que en el caso de las Tensiones, podremos desarrollar también un método
gráfico para el cálculo de las deformaciones
CASO PARTICULAR: DEFORMACIONES PLANAS
Supongamos conocidas las tres componentes del estado de deformaciones plano en un
punto O: εx, εy, γxy, y se quieren calcular, gráficamente, las deformaciones: ε y γ/2
correspondientes en una dirección cualquiera OD, definida por su vector unitario:
u (cosα, cosβ)
y
D
β = 90-α D´
ε
γ/2
β Do
u δ Do´
α
O x
Fig. 2.14
Se sabe, por lo visto en 2.3., que para cada dirección OD se obtendrían por las
ecuaciones analíticas (2.7) y (2.6), un par de valores: ε y γ/2. Así:
para α = α1 → dirección OD1 → ε1 , γ 1 / 2
para α = α 2 → dirección OD2 → ε2,γ 2 / 2
.............................................................................
para α = α n → dirección ODn → ε n , γ n / 2
Si representásemos estos valores obtenidos en unos ejes coordenados, en los que en el
eje de abcisas llevásemos las deformaciones longitudinales (ε) y en el de ordenadas, las
deformaciones angulares (γ/2) y uniésemos todos ellos, se demuestra, no lo haremos,
que el lugar geométrico de los mismos es una circunferencia, a la que denominaremos
“Circunferencia de Mohr”
γ/2 (ε2,γ2/2
(ε1,γ1/2)
O ε
(εn,γn/2)
Fig. 2.15
13

43. Tema 2: Deformaciones
Criterios de signos para las deformaciones, al utilizar el método gráfico de Mohr
• Deformaciones longitudinales (ε): se consideran positivas las deformaciones
longitudinales cuando indican un alargamiento. Negativas en caso contrario.
D D
ε>0
1 Do´ ε<0
Do 1 Do
O O Do´
Fig. 2.16
• Deformaciones angulares (γ/2): se consideran positivas cuando impliquen un
giro en sentido horario. Negativas en caso contrario.
γ/2 > 0 γ/2 < 0
D D´ D´ D
O O
Fig. 2.17
Observaciones:
Como las tensiones cortantes (τ) son las que producen las deformaciones angulares
(γ/2), se observa por lo visto en la sección 1.5 del tema de Tensiones, que hay
coherencia con los criterios de signos dados para las tensiones cortantes y el dado ahora
para las deformaciones angulares: τ > 0 → γ/2 > 0
τ
τ τ
τ τ τ > 0 → γ/2 > 0
τ τ
τ
Fig.2.18
Los criterios de signos utilizados para las deformaciones angulares, en la representación
gráfica de Mohr, no coinciden con los dados en 2.3. para la resolución analítica. Este
hecho habrá de tenerse siempre en cuenta en la resolución de los problemas.
14

44. Sección 2.5: Representación de Mohr
Ejemplo:
y γyx/2 > 0 y γyx/2 > 0
B B´ B B´
γxy > 0
A´ A´
γxy/2 > 0 γxy/2 < 0
O x O A x
A
Criterio de signos para la Criterio de signos para la
resolución analítica resolución gráfica (Mohr)
Fig. 2.19
Construcción de la circunferencia de Mohr:
Supónganse conocidas las componentes del estado de deformaciones plano en un punto
O: εx, εy, γxy. (Fig.2.20.a) y tracemos unos ejes coordenados en donde en el eje de
abcisas llevaremos las deformaciones longitudinales unitarias (ε) y en el de ordenadas
las deformaciones angulares simétricas (γ/2).
La construcción de la Circunferencia de Mohr relativa a dicho estado de Deformaciones
se hará de una forma similar a como se construyó la Circunferencia de Mohr relativa a
las Tensiones
Las deformaciones relativas al eje X ( εx > 0, γxy/2 < 0, por criterios de signos de Mohr),
estarán representadas en los ejes coordenados por el punto X. A su vez, las
deformaciones correspondientes al eje Y ( εy > 0, γyx/2 > 0, por criterios de signos de
Mohr), estarán representadas en los ejes coordenados por el punto Y. Si unimos, con
una recta, los puntos X e Y, la intersección de ésta con el eje de abcisas (punto C), será
el centro de la circunferencia de Mohr. (Fig.2.20.b)
γ/2
Y
γyx/2 Y
εy γyx/2
δy
εy εx
1 uy O E C D ε
δx γxy/2
ux γxy/2
O 1 εx X X
Fig.2.20.a Fig.2.20.b.
15

45. Tema 2: Deformaciones
Por su construcción, se deduce fácilmente que la Circunferencia de Mohr tendrá por
Centro y Radio los siguientes valores:
εx +εy
Centro : OC =
2
2 2
(2.13)
⎛ ε − ε y ⎞ ⎛ γ xy ⎞
Radio : CX = ⎜ x ⎟ +⎜ ⎟
⎝ 2 ⎠ ⎝ 2 ⎠
Cálculo de las deformaciones ε y γ/2 en una dirección OD cualquiera:
A partir de las componentes del estado de deformaciones plano en un punto O: εx, εy,
γxy, se dibujará en un sistema de ejes coordenados: (ε, γ/2), la circunferencia de Mohr,
tal y como se ha indicado en el apartado anterior, obteniendo su centro y su radio
De lo que se trata ahora es de poder conocer gráficamente las deformaciones ε y γ/2
correspondientes a una dirección OD, definida por su vector unitario: uD (cosα, senα).
Y D γ/2
γyx/2 D
β 2α
εy γ/2 Y
δ ε
uy y γ/2
δ γyx/2
1
1 uD δx ε εx
ux γxy/2 O εy C H ε
α γxy/2
O 1 εx X
X
Fig.2.21
El procedimiento será el siguiente: Para pasar de la dirección OX (definida por uX), a la
dirección OD (definida por uD), se deberá girar, en sentido antihorario, el ángulo α.
Pues bien, para pasar en la circunferencia de Mohr, del punto X, (representativo del
estado de deformaciones de la direccion OX), al punto D, (que representará el estado de
deformaciones de la dirección OD), se tendrá que girar, igualmente en sentido
antihorario, el ángulo 2α.(o sea el doble del anterior).
Mediante este procedimiento las deformaciones en la dirección OD serán pues:
Deformación longitudinal: ε = OH = OC + CH = OC + CD.cos β
Deformación angular: γ/2 = DH = CD.senβ
(los valores de OC “centro” y CD “radio”, se obtendrán de la circunferencia de Mohr)
16

46. Sección 2.5: Representación de Mohr
Cálculo de las deformaciones principales:
Se sabe, por lo visto en (2.4) que las deformaciones principales son las deformaciones
máxima y mínima y que en las direcciones donde aparecen, no hay deformaciones
angulares. Es decir, se cumple: δ =ε, γ/2 = 0.
γ/2
Y
γyx/2 Y
εy γyx/2
δy M
uy ε2 εx M
1 δ1 = ε1 O N εy C E ε1 ε
uM δx γxy/2
1 γxy/2 2ϕ1
ϕ1 ux
O 1 εx X X
Fig.2.22
Observando la Circunferencia de Mohr, se ve que los puntos M y N corresponden a las
deformaciones máximas y mínimas y en ellos no hay deformaciones angulares, por
tanto esos puntos estarán representando a las deformaciones principales. Sus valores
serán:
2 2
εx + εy ⎛ ε x − ε y ⎞ ⎛ γ xy ⎞
δ1 = ε1 = OM = OC + CM = Centro + Radio = + ⎜ ⎟ +⎜ ⎟ → MAX
2 ⎝ 2 ⎠ ⎝ 2 ⎠
2 2
εx + εy ⎛ ε − ε y ⎞ ⎛ γ xy ⎞
δ 2 = ε 2 = ON = OC − CN = Centro − Radio = − ⎜ x ⎟ +⎜ ⎟ → MIN
2 ⎝ 2 ⎠ ⎝ 2 ⎠
(2.14)
Las direcciones principales también se podrán obtener a partir de la circunferencia de
Mohr. Se observa (Fig.2.22), que para pasar del punto X del circulo (representativo del
estado de deformaciones de la dirección OX), al punto M, que es donde se dará la
deformación principal: ε1 = εmax, hay que girar en sentido antihorario el ángulo 2ϕ1. Así
pues para obtener la dirección principal OM, sobre la que se dará dicha deformación
principal, se deberá girar la dirección OX, en el mismo sentido (es decir antihorario), el
ángulo ϕ1.
γ xy
siendo: γ xy
XE 2
tag 2ϕ1 = = = ⇒ ϕ1 (2.15)
CE ε x − ε y ε x − ε y
2
La otra dirección principal, la correspondiente al punto N, donde se dará la deformación
principal mínima: ε2 = εmin, se obtendrá girando la anteriormente hallada otros 90º. (ver
Fig.2.22), es decir en la dirección: ϕ2 = ϕ1 ± 90º (los puntos M y N están a 180º en la
circunferencia).
17

47. Tema 3: Cuerpo Elástico
Tema 3 : CUERPO ELÁSTICO
σ LR
LFi LFf F
LE
LP
O ε
1

48. Tema 3: Cuerpo Elástico
3.1.- INTRODUCCIÓN
La experiencia nos enseña que todo cuerpo bajo la acción de las fuerzas aplicadas, se
deforma y que al suprimir éstas, el cuerpo tiende a recuperar su forma inicial. Esta
propiedad que poseen todos los cuerpos, en mayor o menor grado, se denomina
ELASTICIDAD.
Dependiendo del material del que estén hechos los cuerpos, se tendrá que unos cuerpos
se comportarán más elásticos que otros y a su vez, para un cuerpo de un material
determinado, dependiendo de la magnitud de las fuerzas aplicadas, se comportará total o
parcialmente elástico. Se dirá que se comporta “totalmente elástico” si al retirar la
fuerza a la que está sometido recupera totalmente su forma inicial y “parcialmente
elástico” en caso contrario, es decir que al retirar la fuerza aplicada no recupera
totalmente la forma inicial, dejando en él una deformación permanente.
L L
F F
L+∆L L+∆L
L L´
deformación deformación deformación
elástica permanente elástica
Fig.3.1
Así mismo, en nuestro análisis, admitiremos que los cuerpos son ISÓTROPOS, es
decir, que sus propiedades elásticas son iguales en cualquier dirección. Esto no ocurre
exactamente por ejemplo en materiales fibrosos como la madera, ni en materiales
formados por laminación. En estos materiales habrá que hacer un estudio específico de
los mismos, aunque en muchos casos, los resultados que se obtienen con esta hipótesis
son satisfactorios.
3.2.- RELACIONES ENTRE TENSIONES Y DEFORMACIONES. LEY DE
HOOKE GENERALIZADA
Se ha visto en los temas 1º y 2º que en un cuerpo sometido a fuerzas exteriores, a cada
punto del mismo, le corresponde un “estado de tensiones” y un “estado de
deformaciones”. Siendo unas, consecuencia de las otras, es evidente que ha de existir
una relación entre ambos estados. Fue Hooke el que dedujo dichas relaciones.
2

49. Sección 3.2.: Relaciones entre tensiones y deformaciones. Ley de Hooke generalizada
LEY DE HOOKE
“Existe proporcionalidad entre las componentes del estado de tensiones y las
componentes del estado de deformaciones”.
Los coeficientes que regulan dicha proporcionalidad dependen de las constantes físicas
del material y no de las particularidades geométricas del cuerpo.
Para estudiar la deformación del paralelepípedo elemental debida a la acción de las
tensiones, utilizaremos el Principio de Superposición.
y σy
τyz τyx
τxy
σx τzy σx
τxz
τzx
σz x
O
z
σy
Fig.3.2
Deformaciones debidas a σx:
Experimentalmente se ha demostrado que las tensiones normales σ, actuando sobre las
caras opuestas del paralelepípedo sólo originan deformaciones longitudinales ε según
las aristas del paralelepípedo y no producen ninguna deformación angular.
y
D
D´
C´ C
σx σx
O
x
A´ A B B´
z
Fig.3.3
Según la Ley de Hooke: las deformaciones longitudinales ε, son proporcionales a las
tensiones normales σ que las producen:
∆Lx A´ B´ − AB 1 1
ε1x = = = .σ x → Cte proporcionalidad =
Lx AB E E
3

50. Tema 3: Cuerpo Elástico
Siendo E = MÓDULO DE ELASTICIDAD LONGITUDINAL. Es una constante física
de cada material y se obtiene experimentalmente. Sus dimensiones son: N/mm2
Según se observa en la figura (3.3), el alargamiento longitudinal ε1x debido a la tensión
normal σx, va acompañado de acortamientos longitudinales en dirección de los ejes y y
z, que según la ley de Hooke vienen dados por:
∆L y A´C ´ − AC σ
ε1y = = = −ν .ε 1 x = −ν . x
Ly AC E
∆Lz A´ D ´ − AD σ
ε 1z = = = −ν .ε 1 x = −ν . x
Lz AD E
siendo υ = COEFICIENTE DE POISSON. Es también una constante física de cada
material y es adimensional.
De igual forma que hemos obtenidos las deformaciones debidas a la tensión normal σx,
se obtendrían las deformaciones debidas a las tensiones normales σy y σz:
Deformaciones debidas a σy:
σy σy
ε2y = ε 2 x = ε 2 z = −ν .ε 2 y = −ν .
E E
Deformaciones debidas a σz:
σz σz
ε 3z = ε 3 x = ε 3 y = −ν .ε 3 z = −ν .
E E
y aplicando el Principio de Superposición, las deformaciones debidas a las tensiones
normales: σx, σy y σz, serán:
σx ⎛σ y σz ⎞
ε x = ε 1x + ε 2 x + ε 3 x = − ν .⎜
⎜ E + E ⎟
⎟
E ⎝ ⎠
σy ⎛σ σ ⎞
ε y = ε1y + ε 2 y + ε 3 y = − ν .⎜ x + z ⎟ (3.1)
E ⎝ E E ⎠
σ ⎛σ σy ⎞
ε z = ε 1z + ε 2 z + ε 3 z = z − ν .⎜ x +
⎜ E ⎟
E ⎝ E ⎟⎠
Ecuaciones que nos relacionan las deformaciones longitudinales ε, con las tensiones
normales σ.
4

51. Sección 3.2.: Relaciones entre tensiones y deformaciones. Ley de Hooke generalizada
Deformaciones debidas a τxy:
También se ha demostrado experimentalmente que las tensiones cortantes τ, actuando
sobre las caras del paralelepípedo, originan deformaciones angulares γ.
y
τyx
B B´
γyx/2
τxy τxy
A´
γxy/2
O A x
τyx
Fig.3.4
Según la ley de Hooke: las deformaciones angulares γ son proporcionales a las tensiones
cortantes τ:
AA´ 1 1
γ xy ≅ tagγ xy = = .τ xy → Cte proporcion alidad =
OA G G
siendo G = MÓDULO DE ELASTICIDAD ANGULAR. Es una constante física de
cada material y se obtiene experimentalmente. Sus dimensiones son: N/mm2.
De igual forma que hemos obtenidos las deformaciones debidas a la tensión cortante τxy,
se obtendrían las deformaciones debidas a las tensiones cortantes τyx y τzx:
Deformaciones debidas a τxy y a τzx : τ yz τ zx
γ yz = γ zx =
G G
y aplicando el Principio de Superposición, las deformaciones debidas a las tensiones
cortantes: τxy, τyz y τzx, serán:
τ xy τ yz τ zx
γ xy = γ yz = γ zx = (3.2)
G G G
Ecuaciones que nos relacionan las deformaciones angulares γ, con las tensiones
cortantes τ.
5

52. Tema 3: Cuerpo Elástico
Así pues el resumen de ecuaciones que relacionan las tensiones y deformaciones
obtenidas en (3.1) y (3.2), y dadas por la Ley de Hooke generalizada son:
σx ⎛σ y σ z ⎞ τ xy
εx = ⎜ E + E ⎟
− ν .⎜ ⎟ γ xy =
E ⎝ ⎠ G
σy ⎛σ σ ⎞ τ yz
εy = − ν .⎜ x + z ⎟ γ yz = (3.3)
E ⎝ E E ⎠ G
σy ⎞ τ zx
σz ⎛σ γ zx =
εz = − ν .⎜ x +
⎜ E ⎟
E ⎟
G
E ⎝ ⎠
Las relaciones inversas son:
σ x = λ .e3 + 2.G.ε x τ xy = γ xy .G
σ y = λ .e3 + 2.G.ε y τ yz = γ yz .G (3.4)
σ z = λ .e3 + 2.G.ε z τ zx = γ zx .G
siendo: E.ν
e3 = ε x + ε y + ε z (3.5) λ= (3.6)
(1 + ν )(1 − 2.ν )
.
Observación: Las constantes físicas: E, G y υ, están relacionadas entre ellas mediante la
siguiente ecuación:
E
G= (3.7)
2.(1 + ν )
Valores de E, G y υ, para diversos materiales:
MATERIAL E (N/mm2) G (N/mm2) υ
acero 2,1.105 81000 0,3
aluminio (aleacción) 0,73.105 28000 0,33
Madera laminada 1,2.104 0,45
cobre 1,2.105 47000 0,36
6

53. Sección 3.3.: Trabajo de las fuerzas externas
3.3.- TRABAJO DE LAS FUERZAS EXTERNAS
Sea un cuerpo elástico con los vínculos externos suficientes para que no pueda moverse
y apliquemos sobre él, de forma lenta y gradual, las fuerzas: F1, F2,.. Fi,…Fn,
que originarán los desplazamientos: ∆1, ∆2,… ∆i,… ∆n, de sus puntos de aplicación.
Sean: δ1, δ2,… δi,… δn, las componentes de dichos desplazamientos en la dirección de
las fuerzas respectivas.
Fi
F1 i
δi
1 ∆1 ∆i
1´ i´´ i´
δ1
R1 2´ n´ R2
∆2 ∆n
δ2 δn
2 n
F2 Fn
Fig. 3.5
Tengamos a continuación las siguientes consideraciones:
• La aplicación lenta y gradual de las fuerzas hace que los desplazamientos de las
partículas del cuerpo, los hagan con velocidades muy pequeñas y por
consiguiente puede despreciarse la energía cinética producida (Téngase en
cuenta, por ejemplo, que la carga que recibe un pilar de un edificio desde que se
construye el pilar hasta que se termina el edificio, al cabo de varios meses, va a
ir aumentando de forma muy lenta y gradual).
• Se supone despreciable el rozamiento con los enlaces externos
Debido a estas consideraciones se podrá admitir que: “ todo el trabajo que realizan las
fuerzas externas: Te, se invierte totalmente en deformar al cuerpo, transformándose en
Energía de Deformación:U”.
Es decir: Te = U (3.8)
y al no existir disipación de energía, estaremos en el caso de un sistema conservativo y
en consecuencia: “ el trabajo que realizan las fuerzas exteriores depende únicamente de
sus valores iniciales y finales y no del orden en que son aplicadas”.
Cálculo de Te:
Al aplicarse las fuerzas externas de un modo gradual, sus valores en un estado
intermedio, valdrán:
α .F1 , α .F2 ,.....α .Fi ,....α .Fn siendo : 0 ≤ α ≤ 1
7

54. Tema 3: Cuerpo Elástico
y según la ley de Hooke, en ese instante intermedio, las componentes δ de los
desplazamientos de sus puntos de aplicación serán:
α .δ 1 , α .δ 2 ,.....α .δ i ,....α .δ n siendo : 0 ≤ α ≤ 1
Con lo cual, el trabajo elemental que realizarán las fuerzas externas será:
dTe = α .F1.d (α .δ 1 ) + α .F2 .d (α .δ 2 ) + .....α .Fi .d (α .δ i ) + .......α .Fn .d (α .Fn ) =
= ( F1.δ 1 + F2 .δ 2 + ...... Fi .δ i + ...... Fn .δ n ).α .dα
1
int egrando : Te = ( F1 .δ 1 + F2 .δ 2 + ..... Fi .δ i + ...... Fn .δ n ).∫ α .dα
0
y queda finalmente:
1 n
(3.9) Te = .∑ Fi .δ i
2 i =1
Observación: Si en lugar de las fuerzas Fi aplicadas, aplicásemos momentos Mi, que
produjeran giros θi en su misma dirección, la expresión del trabajo sería:
1 n
Te = .∑ M i .θ i (3.10)
2 i =1
3.4.- ENERGÍA DE DEFORMACIÓN
La energía de deformación de un cuerpo elástico, la podremos obtener sumando las
energías de deformación de cada uno de los paralelepípedos elementales que lo forman.
Aislemos pues, de un cuerpo elástico, uno paralelepípedo elemental de lados: dx, dy, dz.
y σy
dz τyz τyx
τxy
σx τzy σx
dy τxz
τzx
σz x
O
z dx
σy
Fig.3.6
El trabajo que realizarán las diferentes fuerzas elásticas que actúan sobre el
paralelepípedo serán:
8

55. Sección 3.4: Energía de deformación
Sobre las dos caras perpendiculares al eje X:
1 1 γ xy 1 γ
.σ x .dy.dz.ε x .dx + .τ xy .dy.dz. .dx + .τ xz .dy.dz. xz .dx =
2 2 2 2 2
1⎛ γ γ ⎞
= .⎜ σ x .ε x + τ xy . xy + τ xz . xz ⎟.dx.dy.dz
⎜
2⎝ 2 2 ⎟⎠
Y repitiendo lo mismo sobre las dos caras perpendiculares al eje Y y las dos caras
perpendiculares al eje Z, quedará:
1
dTe = dU = .(σ x .ε x + σ y .ε y + σ z .ε z + τ xy .γ xy + τ xz .γ xz + τ yz .γ yz ).dx.dy .dz
2
La energía de deformación por unidad de volumen será:
dU 1
u= = .(σ x .ε x + σ y .ε y + σ z .ε z + τ xy .γ xy + τ xz .γ xz + τ yz .γ yz ) (3.11)
dVol 2
Si sustituimos las deformaciones en función de las tensiones, según las ecuaciones 3.3
de la ley de Hooke generalizada
σx ⎛σ y σ z ⎞ τ xy
εx = ⎜ E + E ⎟
− ν .⎜ ⎟ γ xy =
E ⎝ ⎠ G
σy ⎛σ σ ⎞ τ yz
εy = − ν .⎜ x + z ⎟ γ yz =
E ⎝ E E ⎠ G
σy ⎞ τ zx
σz ⎛σ γ zx =
εz = − ν .⎜ x +
⎜ E ⎟
E ⎟
G
E ⎝ ⎠
quedará finalmente como expresión de la Energía de Deformación por unidad de
volumen:
u=
1
2 .E
[
. σ x + σ y + σ z2 − 2.ν .(σ x .σ y + σ x .σ z + σ y .σ z ) +
2 2
]
1
2.G
2
(
. τ xy + τ yz + τ zx
2 2
) (3.12)
La Energía de Deformación U del cuerpo elástico total será: U = ∫ u.d (Vol ) (3.13)
vol
Observación: En las fórmulas obtenidas no hemos considerado el Trabajo debido a las
Fuerzas de Gravedad que actuarían sobre el paralelepípedo, debido a que obtendríamos
un infinitésimo de 4º orden, que se despreciaría frente al Trabajo de las Fuerzas
Elásticas que es de 3º orden, como se ha visto.
9

56. Tema 3: Cuerpo Elástico
3.5.- DIAGRAMAS DE TENSIONES – DEFORMACIONES
Las propiedades mecánicas de los materiales, tales como: RESISTENCIA, RIGIDEZ,
DUCTILIDAD, …………., se obtienen de los Diagramas Tensiones - Deformaciones
Estos diagramas se obtienen a partir de una probeta de dimensiones normalizadas del
material a ensayar y sometiéndola a esfuerzos crecientes de Tracción (o en su caso de
Compresión) hasta llegar a romperla. Durante el proceso se irán midiendo en cada
instante los valores de la tensión a la que esté sometida: σ = F/Ao y las correspondientes
deformaciones que se van produciendo: ε = ∆L/L.
Ao : área inicial de la
sección transversal
F F
L
Fig.3.7
Si en unos ejes coordenados llevamos las deformaciones ε al eje de abcisas y las
tensiones σ al de ordenadas se obtendrá un gráfico que es el Diagrama de tensiones –
deformaciones. Cada material tendrá su propio Diagrama.
El Diagrama tensiones – deformaciones para el caso de un acero estructural, conocido
también como acero dulce de construcción, uno de los metales mas usados en edificios,
puentes, grúas, etc…, es el siguiente:
σ LR
LFi LFf F
LE
LP
O ε
Fig.3.8
Observación: Este diagrama no está dibujado a escala, pero se representa así, para
destacar con más claridad los puntos y partes mas significativas del mismo.
Analicemos pues dicho Diagrama:
10

57. Sección 3.5: Diagramas de tensiones-deformaciones
Tramo O – LP:
Este tramo inicial es una recta y existirá por tanto proporcionalidad entre tensiones σ y
deformaciones ε, se cumple pues la Ley de Hooke: σ σ
ε = →E=
E ε
σ LR
LFi LFf F
LE
σP LP
LP : Límite de Proporcionalidad
σ σP : Tensión de proporcionalidad
tag α = σ/ε = E (Módulo de Elasticidad
longitudinal)
α
O ε ε
Fig.3.9
La pendiente de la recta de proporcionalidad nos proporciona el Módulo de Elasticidad
longitudinal E del material. Y nos va a medir la RIGIDEZ de un material
“Rigidez de un material es la mayor o menor resistencia que opone dicho material a
dejarse deformar”
Ejemplo: Supongamos que tenemos los gráficos de dos materiales representados en la
figura 3.10.
σ σ
LP LP
σ1 σ2 = σ1
α1 α2
ε1 ε ε2 ε
Material 1 Material 2
Fig.3.10
Se observa que la recta de proporcionalidad del material 1 tiene mayor pendiente que la
del material 2: α1 > α2 → tag α1 > tag α2 → E1 > E2 → “el material 1 es más
rígido que el material 2”.
Efectivamente: se observa que sometidos los dos materiales a la misma tensión: σ1 = σ2,
el material 1 se deforma menos que el material 2: ε1 < ε2
11

58. Tema 3: Cuerpo Elástico
Tramo LP - LE:
A partir de LP el diagrama deja de ser una recta y comienza a ser una curva. El punto
LE “límite elástico”, representa la máxima tensión que puede alcanzar el material para
comportarse elásticamente, es decir, sin que se produzcan en él deformaciones
permanentes
σ LR
LFi LFf F
σE
LE
LP
LE : Límite Elástico
σE : Tensión elástica
Campo Elástico
α
O ε
Fig.3.11
Así pues, si una vez alcanzado el punto LE descargamos la probeta, la línea de descarga
se hará recorriendo en sentido contrario la de carga y la probeta volvería a su estado
inicial en el punto O.
σ LR
LFi LFf F
LE
σE
Carga Descarga
α
O ε
Fig.3.12
12

59. Sección 3.5: Diagramas de tensiones-deformaciones
Tramo LE – LFi – LFf :
Una vez alcanzado el punto LE, si seguimos aumentando la carga sobre la probeta, el
diagrama continua curvándose con una pendiente cada vez menor, hasta alcanzar el
punto LFi. y a partir de dicho punto el material se deforma de forma apreciable (puede
observarse a simple vista) sin necesidad de un aumento de carga, con lo cual aparece
una línea horizontal en el gráfico hasta llegar al punto LFf . El material se dice que ha
entrado en fluencia y se vuelve perfectamente plástico
σ LR
LFi LFf F
σF
LE LFi : Límite Fluencia inicial
LP
LFf : Límite Fluencia final
σF : Tensión de fluencia
α
O ε
Fig.3.13
Las deformaciones que sufre la probeta en este tramo son del orden de 10 a 15 veces la
producida hasta el tramo anterior
13

60. Tema 3: Cuerpo Elástico
Tramo LFf – LR - F:
Después de las grandes deformaciones producidas en el material durante el tramo de
fluencia anterior, el material sufre cambios en su estructura cristalina y empieza a
“endurecerse por deformación”, así pues, para seguir deformando la probeta se requiere
de nuevo aumentar la carga que actúa sobre ella. Y así hasta llegar al punto más alto del
diagrama LR, que representará la máxima carga que es capaz de aguantar el material
hasta romperse
LR
σR
LFi LFf F
LE
LP LR : Límite de Rotura
σR : Tensión de rotura
Resistencia a la rotura del material
α
O ε
Fig.3.14
“Resistencia a la rotura de un material es la máxima tensión capaz de soportar hasta
romperse” . (También se la denomina: “resistencia última del material” ).
Hasta llegar al punto LFf, la probeta se va alargando uniformemente en toda su longitud
y este alargamiento va acompañado de una contracción lateral, pero esta contracción
lateral es muy pequeña y apenas significa variación en el valor del área de la sección
transversal inicial Ao, con lo cual no va a suponer un efecto significativo sobre los
valores obtenidos de las tensiones: σ = F/Ao. Pero a partir de LFf, la reducción del área
empieza a ser significativa y llega a ser visible, produciéndose el fenómeno de
“estricción” en una zona concreta de la probeta y produciéndose finalmente la rotura en
el punto F del diagrama.
región de fractura
F F
región de estricción
Fig.3.15
14

61. Sección 3.5: Diagramas de tensiones-deformaciones
Si a partir de LFf, en lugar de obtener las tensiones tomando como referencia el área
inicial de la sección de la probeta: σ = F/Ao, tomásemos el área verdadera de la sección
de la probeta en cada instante: σ = F/A, el diagrama, por lo dicho antes, se mantendría
prácticamente igual hasta LFf, a partir de él, al empezar a ser significativas las
reducciones de la sección transversal, el diagrama tomaría la línea azul que se indica en
la figura siguiente y en lugar de decrecer la curva de LR a F, seguiría creciendo e iría de
LR a F´ y este sería el verdadero diagrama de tensiones-deformaciones. No obstante
este cambio no se considera.
F´
LR
σR
LFi LFf F
LE
LP LR : Límite de Rotura
σR : Tensión de rotura
Resistencia a la rotura del material
α
O ε
Fig.3.16
Del Diagrama se observa las grandes deformaciones permanentes que ha sufrido el
material antes de romperse. Pues bien la propiedad que define esto se denomina:
Ductilidad
“Ductilidad de un material es la capacidad que tiene para sufrir deformaciones
permanentes antes de romperse” .
Se puede obtener midiendo la longitud de la probeta antes y después del ensayo ( una
vez rota), mediante la siguiente fórmula:
F F F
F
L L+∆L
Fig.3.17
∆L
ductilidad : .100 (3.14)
L
15

62. Tema 3: Cuerpo Elástico
Si representásemos el Diagrama a escala natural, se observarán las grandes
deformaciones que se producen hasta la rotura final comparadas con las deformaciones
apenas apreciables que se producen hasta el límite elástico
σ LR
LFi F
LE
LFf
LP
O ε
Fig.3.18
Se observa que los puntos LP, LE y LF están todos ellos muy próximos.
Así pues en el caso que nos ocupa del acero dulce, a efectos prácticos, se suelen tomar
los tres puntos en uno solo, de tal forma que: LP = LE = LF. En consecuencia el
diagrama a efectos prácticos se podrá simplificar de la siguiente manera:
σ
LR
fu
F
fy
LP = LE = LF
σP ≅ σE ≅ σF = fy “resistencia elástica del
material” o “tensión del límite elástico”
σR = fu “resistencia a la rotura del material”
o “tensión de rotura”
O ε
Fig.3.19
Esta situación no se da en otros materiales.
16

63. Sección 3.5: Diagramas de tensiones-deformaciones
Otras consideraciones sobre el Diagrama
Elasticidad - Plasticidad
Supongamos que sobrepasamos el punto LE (límite elástico) y nos encontramos en el
punto A del diagrama y una vez en él, descargamos la probeta. Durante la descarga se
sigue la línea recta AA´, paralela a la recta de proporcionalidad O-LP. Cuando se
alcanza el punto A´, se ha suprimido por completo la carga, pero el material queda con
una “Deformación Permanente: OA´”. En este caso se dice que el material es
“parcialmente elástico”.
σ LR
A
LFi LFf
LE F
LP
Descarga Carga
ZE ZP
α
O A´ A´´ ε
Deformación permanente
Deformación elástica
Deformación total
Fig.3.20
Así se tendrá:
OA´´ : Deformación total que tendrá la probeta al alcanzar el punto A del diagrama
OA´ : Deformación permanente o residual con la que quedará la probeta al descargarla
A´A´´ :Deformación elástica, parte de la deformación total que recupera al descargarla
La característica de un material por la cual sufre deformaciones inelásticas más allá de
la deformación en el límite elástico (LE), se conoce como: “plasticidad “Así pues en el
diagrama distinguiremos dos zonas: la zona elástica (ZE) y la zona plástica (ZP)
17

64. Tema 3: Cuerpo Elástico
Si el material permanece dentro de la zona elástica, puede cargarse, descargarse y
volverse a cargar sin un cambio significativo en su comportamiento; sin embargo,
cuando se carga en la zona plástica, la estructura interna del material se altera y sus
propiedades cambian. Por ejemplo, supongamos como en el caso anterior que hemos
cargado la probeta hasta el punto A y al llegar a dicho punto la descargamos. Ya hemos
visto que el material en la descarga alcanza el punto A´ y ha quedado con una
deformación permanente. Pues bien, si ahora le volvemos a cargar de nuevo, la línea de
carga es de nuevo la A´A y al llegar de nuevo al punto A sigue el diagrama original de
tensión-deformación hasta el punto F
σ LR
A
LFi LFf
LE F
LP
Descarga Carga
ZE ZP
α
O A´ A´´ ε
Deformación permanente
Deformación elástica
Deformación total
Fig.3.21
Se observa que en la nueva carga el material se comporta de manera linealmente elástica
hasta el punto A (superior al punto LE), con lo cual el material mejora su
comportamiento elástico, pero por el contrario su zona plástica se reduce. Este nuevo
comportamiento encuentra aplicaciones por ejemplo en los cables de los ascensores.
Diagramas de otros materiales
El diagrama tensiones-deformaciones, visto anteriormente, es el correspondiente a un
acero estructural, conocido también como acero dulce de construcción. Otros materiales
darán lugar a otros diagramas. Veamos a continuación los diagramas correspondientes a
tres prototipos de materiales: el acero dulce de construcción (ya visto), las aleaciones de
aluminio y el hormigón y destaquemos las diferencias principales que hay entre ellos
18

65. Sección 3.5: Diagramas de tensiones-deformaciones
Acero dulce de construcción
material muy dúctil (sufre grandes
LR
σ deformaciones permanentes antes de
LE
LFi LFf F romperse)
LP
Observación: este acero es de bajo
contenido en carbono. Si aumentamos el
contenido en carbono se vuelve menos
dúctil pero mas resistente.
O ε
presenta un punto de fluencia bien
Fig.3.22 definido
Aleacciones de aluminio
σ
LR material dúctil
LF
LE
LP
no presenta un punto de fluencia definido
Observación: en estos casos se suele definir
un punto de fluencia en el diagrama y se
obtiene trazando una línea paralela a la recta
de proporcionalidad para una deformación de
O 0,002 ε
0,002 (0,2 %)
Fig.3.23
Hormigón, Vidrio, Cerámicas….
material frágil ( muy poco dúctil).
Los materiales frágiles se rompen con poco
σ LR
alargamiento después de que se ha excedido el
límite de proporcionalidad. Por lo tanto la rotura
LP aparece bruscamente, sin previo aviso
O ε
Fig.3.24
19

66. Tema 3: Cuerpo Elástico
Ensayo de Compresión
El ensayo a compresión se realiza colocando una probeta cilíndrica o prismática entre
los platos de una prensa.
Fig.3.25
Las curvas tensión-deformación para el ensayo a compresión difieren de las del ensayo
a tracción.
Así, en los materiales dúctiles, las partes iniciales de ambos diagramas son parecidas,
pero a partir de la fluencia difieren bastante. En el ensayo a tracción la probeta se va
alargando y termina por romper, en cambio en el ensayo a compresión, la probeta se va
acortando y abombando lateralmente y se aplana, sin producirse la rotura.
Fig.3.26
El prototipo de diagrama a compresión de un material dúctil sería pues:
LR (compresión)
σ
σ
LF LR (tracción)
LE
LP
LP
O ε
O 0,002 ε
Fig.3.27 Fig.3.28
En los materiales frágiles, el diagrama correspondiente al ensayo a compresión presenta,
una parte inicial igual que el de tracción, pero la tensión de rotura se suele alcanzar para
valores más elevados
20

67. Sección 3.6: Coeficientes de seguridad
3.6.- COEFICIENTES DE SEGURIDAD
Según la normativa CTE se deberán aplicar dos coeficientes de seguridad, uno para
minimizar las tensiones límites del material y otro para mayorar las cargas aplicadas.
Coeficiente de minoración de la tensión límite del material
Ya hemos visto que al aumentar las cargas que actúan sobre un cuerpo aumentan las
tensiones en los puntos de su interior, debiendo evitar que las mismas alcancen los
valores correspondientes a las tensiones límites del material. En el caso de los
materiales dúctiles, como es el caso del acero, para el valor de dicha tensión límite se
suele adoptar la tensión del límite elástico (resistencia elástica): fy y en el caso de los
materiales frágiles, como sería el caso del hormigón, se tomará como valor de la
tensión límite, la tensión límite de rotura (resistencia a la rotura): fu
Con el objeto de tener en cuenta la mayor o menor precisión de las tensiones límites
marcadas por los fabricantes, valores característicos para los distintos materiales, se
introduce un coeficiente de seguridad que minimiza dichos valores.
Así por ejemplo en el caso del acero, al ser un material homogéneo, los valores de las
tensiones límites indicadas por los fabricantes suelen ser bastante precisas, con lo cual
se usan unos coeficientes de seguridad pequeños para minorar las tensiones límites:
σ
fy LE ≅ LF
fyd
fy
f yd = (3.15)
γM
O ε
material dúctil
Fig.3.29
siendo:
f yd : tensión del límite elástico para el cálculo
f y : tensión del límite elástico indicado por los fabricantes (ver tabla 3.1)
γ M = coeficiente de seguridad del material = 1, 05;1,1;1, 25;1, 4
Tabla 3.1 de las características mecánicas mínimas de los aceros
Espesor nominal t (mm)
Designación Tensión del límite elástico Tensión de rotura
del tipo de acero fy (N/mm2) fu (N/mm2)
t≤16 16≤t≤40 40≤t≤63 3≤t≤100
S235 235 225 215 360
S275 275 265 255 410
S355 355 345 335 470
S450 450 430 410 550
21

68. Tema 3: Cuerpo Elástico
Para el caso de los hormigones, al ser un material heterogéneo, los coeficientes de
minoración de las tensiones límites son más grandes, al ser éstas más imprecisas.
σ
fu LR
fu (3.16)
fud fud =
γM
O
ε
material frágil
Fig.3.30
siendo:
f ud : tensión del límite de rotura para el cálculo
fu : tensión del límite de rotura indicado por los fabricantes
γ M : coeficiente de seguridad del material = 1, 7; 2; 2, 2; 2,5; 3 .
(este coeficiente dependerá de la categoría del control de su fabricación y de su ejecución.)
Ver normativa CTE-SE-F
Coeficiente de mayoración para las cargas aplicadas
Dado que en la determinación de las cargas que actúan sobre una determinada barra o
estructura, no se pueden obtener muchas veces sus valores exactos, es conveniente
mayorar éstas, multiplicándolas por un coeficiente de seguridad, y trabajar con valores
mayores para suplir esas posibles diferencias entre el valor real que tendrá una carga y
el valor que nosotros hayamos obtenido.
Así por ejemplo, en la carga que transmite la nieve o el viento sobre una edificación,
nosotros trabajaremos con valores estadísticos, que se obtienen según la zona geográfica
donde nos encontremos, su altitud y su ubicación dentro de esa zona. Dichos valores
están recogidos en las Normativas (CTE-SE-AE). Pero es evidente que nos podremos
encontrar en casos ocasionales en que se puedan superar los valores indicados en las
Normativas. De ahí esa necesidad de mayorar los valores característicos de las cargas
que nos dan las Normativas.
Otro caso que ocurre con frecuencia es por ejemplo, en los casos de impactos o de
vibraciones transmitidas por maquinaria o bien por terremotos, tampoco se dispone de
unos cálculos demasiado precisos para determinar con exactitud las cargas que como
consecuencia de ellos se transmiten a la barra o estructura.
Es evidente que cuanto mayor sea la incertidumbre en el conocimiento del valor de una
carga, mayor debe de ser el coeficiente de seguridad con el que mayoremos la carga. No
obstante en las cargas que se transmiten a las edificaciones en general, las Normativas
ya fijan los coeficientes de seguridad para la mayoración de las cargas que debemos
aplicar.
22

69. Sección 3.6: Coeficientes de seguridad
Así pues las cargas a considerar en los cálculos serán las cargas mayoradas:
P* = P.γ (3.17)
siendo :
P* : Carga mayorada (con la que se trabajará en los cálculos)
P : Carga aplicada (valor característico)
γ : Coeficiente de seguridad para las cargas (ver tabla 3.2 )
Observaciones:
1) En la normativa CTE-SE se indican los coeficientes de seguridad a emplear en las
edificaciones:
Tabla 3.2 de coeficientes parciales de seguridad (γ) para las acciones (cargas)
Tipo de verificación Tipo de acción Situación persistente o transitoria
Favorable Desfavorable
Permanente
-Peso propio, peso del terreno 1,35 0,8
Resistencia -Empuje del terreno 1,35 0,7
-Presión del agua 1,2 0,9
Variable: viento, nieve,… 1,5 0
Tipo de verificación Tipo de acción Situación persistente o transitoria
Desestabilizadora Estabilizadora
Permanente
-Peso propio, peso del terreno 1,1 0,9
Estabilidad -Empuje del terreno 1,35 0,8
-Presión del agua 1,05 0,95
Variable: viento, nieve,… 1,5 0
2) Cuando sobre una barra o estructura actúan varias acciones (cargas)
simultáneamente, los coeficientes de seguridad de las mismas pueden sufrir reducciones
en sus valores. Ver normativas CTE-SE. Y CTE-AE
3) La mayoración de cargas se empleará para las comprobaciones de resistencia y de
estabilidad. En cambio para las comprobaciones de las deformaciones se emplearán las
cargas sin mayorar.
23

70. Tema 3: Cuerpo Elástico
3.7.- CRITERIOS PARA EL DIMENSIONAMIENTO DE SECCIONES A
RESISTENCIA
1.-Criterio elástico de dimensionamiento:
La resistencia elástica de una sección se obtendrá cuando en un punto de la misma se
alcance la tensión del límite elástico fy. (Este criterio se desarrollará en los siguientes
temas)
F1
S
fy
F4
F2
Fig. 3.31
2.-Criterio plástico de dimensionamiento:
La resistencia plástica de una sección se obtendrá cuando en todos los puntos de la
misma se alcance la tensión del límite elástico fy. (Este criterio se desarrollará en los
siguientes temas)
F1
fy
S
fy
F4
F2 fy
Fig. 3.32
24

71. Sección 3.7: Criterios para el dimensionamiento de secciones a resistencia
3.-Criterio de Von Mises de dimensionamiento:
Este criterio era el que se venía aplicando con la Normativa anterior.
Esta teoría esta basada en lo siguiente: “La energía de deformación que absorbe un
cuerpo se emplea en producir en él un cambio de volumen y unas deformaciones
angulares en las caras de los paralelepípedos elementales que lo forman”
Y esta teoría dice: “Un cuerpo falla elásticamente cuando la energía que se emplea en
las deformaciones angulares, alcanza el valor de ésta obtenido en el ensayo a tracción,
cuando en la probeta se alcanza la tensión del límite elástico fy
Para ver la fórmula que expresa esta teoría partimos de un paralelepípedo sometido a
sus tres tensiones principales: σ1>σ2>σ3
σ2 σm σ2-σm
σ1 σ1-σm
σm
= +
σ3 σm σ3-σm
(a) (b) (c)
Fig.3.33
El paralelepípedo de la fig.3.33.a., absorberá una energía de deformación U, que se
invertirá, por lo anteriormente dicho, en un incremento de volumen del paralelepípedo
U∆vol y en una deformación angular de sus caras: Ud.
Así pues resultará:
U = U ∆vol + U d (3.18)
Si sometemos al paralelepípedo a una tensión media σm dada por:
σ1 + σ 2 + σ 3
σm = (3.19)
3
este estado de tensiones, (ver fig.3.33.b), tan sólo proporcionará al paralelepípedo un
cambio de volumen: U∆vol, con lo cual el estado de tensiones de la fig.3.33.c, será el que
proporcionará la energía de deformación necesaria para las deformaciones angulares de
sus caras: Ud.
Por la ecuación (3.12) para obtener la energía de deformación, vista en la sección 3.4,
tendremos que:
U =
1
2 .E
[ 2 2
]
. σ x + σ y + σ z2 − 2.ν .(σ x .σ y + σ x .σ z + σ y .σ z ) +
1
2.G
(
. τ xy + τ yz + τ zx
2 2 2
)
25

72. Tema 3: Cuerpo Elástico
Para el estado de tensiones del paralelepípedo planteado en la fig.3.31.a, sería:
σ x = σ 1 τ xy = 0
σ y = σ 2 τ yz = 0
σ z = σ 3 τ zx = 0
con lo cual la ecuación (3.12) quedaría:
1
U = . ⎡σ 12 + σ 2 + σ 32 − 2.ν .(σ 1 .σ 2 + σ 1 .σ 3 + σ 2 .σ 3 ) ⎤
2
(3.20)
2.E ⎣ ⎦
Para el caso del paralelepípedo de la fig.3.31.b, sería:
σ x = σ m τ xy = 0
σ y = σ m τ yz = 0
σ z = σ m τ zx = 0
con lo cual la ecuación (3.12) quedaría ahora:
1 1
U ∆vol = . ⎡σ m + σ m + σ m − 2.ν .(σ m .σ m + σ m .σ m + σ m .σ m ) ⎤ =
⎣
2 2 2
⎦ 2.E . ⎡ 3.σ m − 2.ν .(3.σ m ⎤ =
⎣
2 2
⎦
2.E
3.σ m
2
= .(1 − 2.ν )
2.E
y sustituyendo σm por su valor: dado en la ecuación (3.19) y operando queda:
1 − 2.ν
U ∆vol = . ⎡σ 12 + σ 2 + σ 32 + 2.σ 1 .σ 2 + 2.σ 2 .σ 3 + 2.σ 3 .σ 1 ⎤
⎣
2
⎦ (3.21)
6.E
Finalmente de la ecuación 3.18:
U = U ∆vol + U d → U d = U − U ∆vol
y sustituyendo las expresiones obtenidas para U y para U∆vol, (ecuaciones 3.20 y 3.21
respectivamente), quedará:
1 +ν ⎡ (σ − σ 2 ) 2 + (σ 2 − σ 3 ) 2 + (σ 3 − σ 1 ) 2 ⎤
U d = U − U ∆vol = .⎢ 1 ⎥ (3.22)
3.E ⎣ 2 ⎦
26

73. Sección 3.7: Criterios para el dimensionamiento de secciones a resistencia
Por otra parte el estado de tensiones de un paralelepípedo elemental para el caso del
ensayo a tracción, cuando la probeta haya alcanzado la tensión del límite elástico será:
σ 1 = f yd
fyd fyd
σ2 = 0
σ3 = 0
Fig.3.34
y sustituyendo en la ecuación 3.22 la energía de deformación angular para este caso
sería:
1 +ν 2
Ud = . f yd (3.23)
3.E
Finalmente si aplicamos esta teoría, se tendrán que igualar las dos expresiones obtenidas
para Ud (ecuaciones 3.22 y 3.23):
1 +ν ⎡ (σ − σ 2 ) 2 + (σ 2 − σ 3 ) 2 + (σ 3 − σ 1 ) 2 ⎤ 1 + ν 2
.⎢ 1 ⎥= . f yd y operando
3.E ⎣ 2 ⎦ 3.E
si (σ 1 − σ 2 ) 2 + (σ 2 − σ 3 ) 2 + (σ 3 − σ 1 ) 2
= f yd → falla
2
Para dimensionar a resistencia con este criterio, según lo visto anteriormente, será:
(σ 1∗ − σ 2 ) 2 + (σ 2 − σ 3 ) 2 + (σ 3 − σ 1∗ ) 2
∗ ∗ ∗ ∗
≤ f yd (3.24)
2
Caso particular: Tensiones planas
Para el caso de tensiones planas si hacemos σ3 = 0 se tendrá:
σ 1∗2 + σ 2 2 − σ 1∗ .σ 2 ≤ f yd
∗ ∗
(3.25)
27

74. Tema 3: Cuerpo Elástico
y por último sustituyendo las tensiones principales σ1 y σ2 en función de las
componentes del estado de tensiones (ecuaciones 1.19):
σ x +σ 1
σ1 = y
+ . (σ x − σ y ) 2 + 4 .τ xy
2
2 2
σ x +σ 1
σ2 = y
− . (σ x − σ y ) 2 + 4 .τ xy
2
2 2
la ecuación 3.25 resultará:
σ x 2 + σ ∗2 − σ x .σ ∗ + 3.τ xy2 ≤ f yd
∗
y
∗
y
∗
(3.26)
Observación: Cuando las tensiones normales sean cero, la fórmula de Von Mises
quedará:
f yd
3.τ xy ≤ f yd
*2
→ τ xy ≤
*
= τ yd (3.27)
3
A esta tensión cortante se la denomina “tensión cortante en el límite elástico”: τyd
28

75. Tema 4: Tracción - Compresión
Tema 4 : TRACCIÓN - COMPRESIÓN
A σx z
σx
F σx x
G
O N= F
σx σx
σx
y
1

76. Tema 4: Tracción - Compresión
4.1.- INTRODUCCIÓN
Una sección de una pieza está solicitada a Tracción-Compresión cuando la resultante de
las fuerzas interiores tiene la componente Rx = N
TRACCIÓN (N>0)
z
Rx= N N x
G x
COMPRESIÓN (N<0)
y
N x
Fig. 4.1
En este tema se estudiará sólidos que sólo trabajen a TRACCIÓN-COMPRESIÓN, es
decir, sólidos en los que en todas sus secciones tan sólo aparezca la componente Rx= N
de las fuerzas interiores.
Ejemplos:
Las BARRAS que componen las cerchas o vigas en celosía
F1
4 1
7 F1
1 5
3
F2 2 F2
2 6
Los CABLES que sujetan barras
F2
1 2 2
F1
1
F2
F1
Fig. 4.2
Los DEPOSITOS o RECIPIENTES a PRESIÓN
2

77. Sección 4.2: Tensiones
4.2.-TENSIONES
Consideremos una barra prismática trabajando a Tracción-Compresión y cortemos por
una sección recta transversal de la misma (A).
z
A
F F F x
A G
O N= F
Fig. 4.3 y
Para ver como se distribuyen las fuerzas internas o tensiones en dicha sección, tomemos
en un punto O (z,y) cualquiera de la sección A, un elemento diferencial de área: dA. Las
tensiones serán, según lo visto en la sección 1.6:
A z
τxz
F G y N= F dA
x O σx
dA
z
O
τxy
y
Fig. 4.4
y según las relaciones tensiones-solicitaciones, ecuaciones (1.26):
N = ∫ σ x .dA = F V y = ∫ τ xy .dA = 0 Vz = ∫ τ xz .dA = 0
A A A
T = ∫ (τ xz . y − τ xy .z ).dA = 0 M y = ∫ σ x . z.dA = 0 M z = ∫ σ x . y.dA = 0
A A A
Se ha tenido en cuenta que al trabajar la sección sólo a Tracción-Compresión: Vy = Vz =
T = My = Mz=0
Con estas 6 ecuaciones por si solas no se podrá determinar las tensiones: σx, τxy, τxz.
Para poder calcularlas se recurrirá a hipótesis
La hipótesis que resuelve la indeterminación del sistema de ecuaciones anteriormente
planteado, es la HIPÓTESIS DE BERNOUILLI o de CONSERVACIÓN DE LAS
SECCIONES PLANAS, que dice: “las secciones transversales del prisma que eran
planas y perpendiculares a su línea medía antes de la deformación, al producirse ésta,
3

78. Tema 4: Tracción - Compresión
se trasladan paralelamente a sí mismas, permaneciendo planas y perpendiculares a
dicha línea media”
Esta hipótesis se puede comprobar experimentalmente sometiendo a Tracción una barra
prismática en la que se han trazado previamente sobre su superficie una retícula de
líneas rectas, unas perpendiculares y otras paralelas al eje longitudinal del prisma
a b a´ b´
F F
c d c´ d´
Fig. 4.5
Se observa que todas las líneas rectas, paralelas al eje longitudinal, alargan por igual,
con lo cual se podrá decir que “la deformación longitudinal unitaria es constante”, es
decir: εX = cte
En virtud de ello y según la ley de Hooke:
σx
εx = = cte → σ x = E.ε x = cte → σx = cte
E
Llevando esta conclusión a la primera de las ecuaciones anteriormente planteadas:
N = ∫ σ x .dA = F ( si σ x = cte) → N = σ x .∫ dA = σ x . A = F de donde :
A A
N F
σx = = = cte σx = cte = F/A
A A A σx z
σx
F σx x
G
O N= F
σx σx
σx
y Fig. 4.6
Se observa igualmente que cualquier rectángulo formado por la retícula de líneas rectas,
por ejemplo el abcd, después de la deformación, se transforma en el rectángulo
a´b´c´d´ y por tanto sigue manteniendo sus ángulos rectos, es decir, no se producen
deformaciones angulares. Así pues: γxy =0 γyz =0 γzx =0
τ xy τ yz τ zx
y por la ley de Hooke: γ xy = =0 γ yz = =0 γ zx = = 0 con lo cual:
G G G
τ xy = 0 τ yz = 0 τ zx = 0
4

79. Sección 4.2: Tensiones
Conclusión: “En una barra prismática que trabaje sólo a TRACCIÓN-COMPRESIÓN,
las componentes del estado de tensiones en un punto cualquiera de la misma serán”:
N F z
σx = = = cte τ xy = 0
A A σx σx x
σy =0 τ yz = 0 (4.1) P
σz =0 τ zx = 0 y
Observación: La sección por donde se corta la barra prismática para obtener las
componentes del estado de tensiones en un punto, es una sección recta transversal, es
decir, perpendicular al eje x de la barra.
z
A
F F N=F
A F G x
O
σx=F/A=cte
Fig. 4.7 y
Pero si en lugar de cortar la barra por la sección recta transversal A, la cortamos por una
sección inclinada B, las tensiones correspondientes las podríamos obtener a partir de las
ecuaciones matriciales (1.9), vistas en la sección 1.3 o bien a través del círculo de Mohr.
B u B
α σ
F G F x F G x
α
O O ρx
Fig. 4.8 τ
Así: conocidas las componentes del estado de tensiones en el punto O, al cortar por la
sección recta transversal A:
N F
σx = = = cte σ y = 0 σ z = 0 τ xy = 0 τ yz = 0 τ zx = 0
A A
La tensión sobre la sección inclinada, B, será:
 ρ x  σ x 0 0 cos α  ρ x = σ x . cos α
ρ  =  0 . senα  → ρ = 0
0 0  (4.2)
 y   y
ρz   0
   0 0  0 
  ρz = 0
Las tensiones normal y cortante serán:
rr
σ = ρ .u = σ x . cos 2 α τ = ρ 2 − σ 2 = σ x . cos α .sen α (4.3)
5

80. Tema 4: Tracción - Compresión
Diagramas de Fuerzas Normales:
Estos diagramas nos dan las fuerzas normales N en cada sección de la barra prismática.
Ejemplo: Representemos los diagramas de fuerzas normales para la barra prismática de
la figura, sometida a las fuerzas F1 y F2 que se indican.
Sección recta
Transversal (A)
F1 F2 F2 F1 x z
G
L1 L2 L3 y
N F1 F1
F1-F2
+ x Fig. 4.9
tramo L1 : tramo L2 :
F1 N = F1 N = F1-F2
F1 F2 x
x
σx = N/A = F1/A = cte
σx = N/A = (F1-F2)/A = cte
tramo L3 :
N = F1 F1
x
σx = N/A = F1/A = cte
6

81. Sección 4.2: Tensiones
Barras prismáticas de sección variable. Concentración de Tensiones:
F F
α
α
Fig. 4.10
Para valores de α pequeños → σx ≅ cte Para valores de α grandes → σx ≠ cte
En general, en las barras prismáticas con variación “brusca” de sección → σx ≠ cte
N N
σmax σmax
σmedia σmedia
m n m n
N Fig. 4.11 N
Ocurre que en los puntos próximos a donde se detecta el cambio “brusco” de sección,
esto es, en los puntos : m y n indicados en las figuras, se producen tensiones superiores
a la tensión media y a medida que nos vamos alejando de ellos, las tensiones van
disminuyendo, llegando a producirse tensiones inferiores a la tensión media en los
puntos mas distantes de ellos. La tensión máxima se obtiene:
N
σ max = k .σ med = k . siendo k ≥ 1 " coeficiente de concentrac ión de tensiones"
A
(4.4)
El valor de k va a depender de:
• Tipo de solicitación: Tracción, Flexión, etc..
• Geometría y dimensiones del cambio de sección
• Tipo de material
y es un valor que se puede obtener experimentalmente
Observación: La concentración de tensiones adquiere mucha importancia en el cálculo
de piezas sometidas a cargas repetidas o de fatiga, pues en estos casos, en los puntos m
y n, donde se concentran las tensiones y donde aparecen las σmax, son los puntos donde
romperán las barras.
7

82. Tema 4: Tracción - Compresión
Para disminuir el efecto de estas concentraciones de tensiones debemos de tratar de
diseñar cambios suaves de sección.
N N
σmax
σmedia
m n σmax
σmedia
m n
N
Fig. 4.12 N
N N
σ max = k .σ med = k . → k >> 1 σ max = k .σ med = k . → k ≈1
A A
4.3.-DEFORMACIONES
Conocidas, en la sección anterior, las “Componentes del estado de tensiones” en un
punto O de una barra prismática que trabaje a Tracción-Compresión, la obtención de las
“Componentes del estado de deformaciones”, en dicho punto, se obtendrán aplicando la
Ley Generalizada de Hooke:
σx
εx = γ xy = 0
E
σx
ε y = −ν . γ yz = 0 (4.5)
E
σx
ε z = −ν . γ zx = 0
E
8

83. Sección 4.3: Deformaciones
Desplazamiento u de una sección de una barra:
Al aplicar a una barra de longitud L, una fuerza F de tracción, ésta sufrirá un
alargamiento total ∆L y cada una de las secciones de la barra sufrirán desplazamientos
u. Los desplazamientos u de las secciones se calcularán de la siguiente forma:
x1 ∆x1 = u
x dx
N
L ∆L
Fig. 4.13
∆(dx) σx
Por definición: ε x = → ∆(dx) = ε x .dx = .dx
dx E
σx
x1 x1 x1
N
u ( x1 ) = ∆x1 = ∫ ∆(dx) = ∫ dx = ∫ .dx
0 0
E 0
A.E
Alargamiento total de la barra ∆L:
L L
σx L
N L
N .dx
∆L = ∫ ∆ (dx) = ∫ .dx = ∫ .dx ∆L = ∫ (4.6)
0 0
E 0
A.E E. A
0
Casos particulares:
N .L
• Si: N = cte A = cte E = cte → ∆L = (4.7)
E. A
• → N i .Li
Si N, A, E, varían pero de forma discreta (a saltos): ∆L = ∑
Ei . Ai
(4.8)
9

84. Tema 4: Tracción - Compresión
4.4.-RESOLUCIÓN DE CASOS HIPERESTÁTICOS
Cuando en una barra o en una estructura el número de ecuaciones de equilibrio es
inferior al número de incógnitas, se dice que es un caso Hiperestático
Nº ECUACIONES EQUILIBRIO < Nº INCÓGNITAS
⇓
CASO HIPERESTÁTICO
Éstos casos suelen darse cuando la barra o la estructura tienen apoyos (ligaduras) de
más.
Para resolver pues un caso hiperestático no serán suficientes las Ecuaciones de
equilibrio y se buscarán para complementarlas Ecuaciones de Deformación, de tal
forma que se cumpla:
Nº ECUACIONES EQUILIBRIO + Nº ECUACIONES DE DEFORMACIÓN =
= Nº INCÓGNITAS
El estudio de este apartado se desarrollará a través de la resolución de varios ejemplos
Ejemplo 1º: Barra empotrada en ambos extremos sometida a una fuerza
RA F RB
L1 L2 Fig. 4.14
Ecuación de equilibrio: ∑F = 0 RA + RB = F (4.9)
Incógnitas: RA, RB
¡ Es un CASO HIPERESTÁTICO ! , tiene apoyos de más (está doblemente empotrada y
con un solo empotramiento sería suficiente).
La barra ISOSTÁTICA sería:
RA F
L1 L2
pero está barra no sería equivalente a la dada, para que fuera equivalente sería:
10

85. Sección 4.4: Resolución de casos hiperestáticos
barra ISOSTÁTICA EQUIVALENTE:
RA F RB con la condición (ecuación de
deformación): ∆L = 0 (4.10)
L1 L2
tramo L1:
N
RA N = RA
RA
+
x
- tramo L2:
RB RB
N = RB
Fig. 4.15
Desarrollando la ecuación (4.10), por la expresión dada en (4.8):
Ni .Li RA .L1 − RB .L2
∆L = 0 → ∆L = ∑ = + =0 (4.11)
Ei . Ai E. A E. A
y resolviendo el sistema de ecuaciones formado por la ecuación de equilibrio (4.9) y la
ecuación de deformación (4.11):
F .L2 F .L1
RA = RB = (4.12)
L1 + L2 L1 + L2
Ejemplo 2º: Barra empotrada en ambos extremos sometida a un incremento de
temperatura: Tensiones de origen térmico
RA RB
∆T>0
L Fig. 4.16
Ecuación de equilibrio: ∑F =0 RA = RB (4.13)
Incógnitas: RA, RB
¡ Es un CASO HIPERESTÁTICO ! , tiene apoyos de más (está doblemente empotrada y
con un solo empotramiento sería suficiente).
11

86. Tema 4: Tracción - Compresión
barra ISOSTÁTICA EQUIVALENTE:
RA RB con la condición (ecuación de
∆T>0 deformación): ∆L = 0 (4.14)
L
tramo 0-x-L:
N
x
Rx = RB RB
-
RB Fig. 4.17
Desarrollando la ecuación (4.14) y aplicando el Principio de Superposición de Efectos:
∆L = 0 → ∆L = ∆L(∆T ) + ∆L( RB ) = 0
∆T>0
∆L( ∆T ) = L.α .∆T
∆L α = coef. dilatación térmico
L
− RB .L
RB ∆L( RB ) =
E. A
∆L
L
− RB .L
∆L = L.α .∆T + =0 (4.15)
E. A
y resolviendo el sistema de ecuaciones formado por la ecuación de equilibrio (4.13) y la
ecuación de deformación (4.15):
R A = RB = E. A.α .∆T (4.16)
y las tensiones que se habrán generado en la barra empotrada por efecto del incremento
de temperatura serían:
N − RB
σx = = = − E.α .∆T (4.17)
A A
Observación: Las tensiones se han originado porque debido al ∆T>0, al querer dilatar la
barra y no poder hacerlo al estar doblemente empotrada, presionará a los
empotramientos y por consiguiente aparecerán las reacciones en éstos. Esto no pasaría
si hubiese habido un solo empotramiento y la barra hubiese podido dilatar libremente
∆T>0 σx = 0
L ∆L
12

87. Sección 4.4: Resolución de casos hiperestáticos
Ejemplo 3º: Barra pretensada de hormigón armado
Dado que el hormigón es un material que resiste muy mal los esfuerzos de tracción,
podremos mejorar su resistencia a la tracción si introducimos en él redondos de acero
previamente traccionados.
El procedimiento será el siguiente:
1ª fase: Se toman redondos de acero y los estiramos sometiéndolos a una fuerza de
tracción de X Kg.
X redondo de acero X
la tensión a que estará sometido el redondo de acero será:
X
σ ´A = siendo AAc = área de la sección del redondo de acero
AAc
2ª fase: Sin destensar todavía los redondos de acero, añadimos el hormigón y
esperamos a que éste fragüe, cuando esto ocurra, el redondo de acero se habrá quedado
totalmente adherido al hormigón. En éste instante destensamos los redondos de acero,
liberándolos de la fuerza X a los que les teníamos sometidos y como consecuencia de
ello el redondo de acero tenderá a acortarse y arrastrará con él al hormigón, provocando
en él una compresión. Asi ocurrirá:
redondo de acero hormigón
X X
L Fig. 4.18
Para calcular la parte de la fuerza X que absorberá tanto el redondo de acero como el
hormigón, se secciona transversalmente la barra y estudiamos el equilibrio de una de las
dos partes seccionadas
F´´H
X
F´´Ac
F´´H
Ecuación de equilibrio: ∑F = 0 X = FAc + FH
´´ ´´
(4.18)
Incógnitas: F´´Ac, F´´H
¡ Es un CASO HIPERESTÁTICO ! , tiene materiales de más. Se añadirá una ecuación
de deformación
13

88. Tema 4: Tracción - Compresión
La ecuación de deformación será, al quedar el redondo de acero y el hormigón
fuertemente adheridos, se acortarán por igual, es decir, se cumplirá:
∆LAc = ∆LH (4.19)
´´
FAc .L F ´´ .L
y desarrollando esta ecuación: = H (4.20)
E Ac . AAc EH . AH
y resolviendo el sistema de ecuaciones formado por la ecuación de equilibrio (4.18) y la
ecuación de deformación (4.20):
E Ac . AAc E H . AH
FAc = X .
´´
FH = X .
´´
(4.21)
E Ac . AAc + E H . AH E Ac . AAc + E H . AH
y las tensiones correspondientes serán:
´´ ´´
FAc E Ac FH EH
σ ´´
=− = −X. σ ´´
=− = −X. (4.22)
E Ac . AAc + E H . AH E Ac . AAc + E H . AH
Ac H
AAc AH
con lo que sumando las tensiones obtenidas en ambos materiales después de estas dos
fases, quedarán:
X E Ac EH
σ Ac = σ ´Ac + σ ´´ = − X. σ H = σ H = −X.
´´
(4.23)
E Ac . AAc + E H . AH E Ac . AAc + E H . AH
Ac
AAc
Conclusiones: la barra de hormigón armado pretensado al estar previamente trabajando
a compresión, como consecuencia del pretensado, mejorará su capacidad para resistir
mayores esfuerzos a tracción. Ésta conclusión se puede apreciar a través del diagrama
tensiones-deformaciones:
σ σ
fu fu
Resistencia Resistencia
a la a la
tracción tracción
O O
ε ε
O´ σH = σ´´H
Fig. 4.19
Hormigón normal Hormigón pretensado
14

89. Sección 4.4: Resolución de casos hiperestáticos
Ejemplo 4º: Defectos de montaje
Se quiere montar la estructura que se indica en la figura 4.20, que estará formada por
tres barras del mismo material (E Kg/cm2) y de la misma sección (A cm2). Las barras se
deberán articular en O
2 1 3
α α L
O
Fig. 4.20
Al tratar de efectuar el montaje se observa que la barra central 1, en lugar de tener la
longitud L, tiene de longitud: L+∆L, con lo cual al ir a acoplarlas en O, se dará la
siguiente situación:
2 1 3
α α L
O
∆L
Fig. 4.21 O´
Se supone que el valor de ∆L es pequeño y el montador, en lugar de serrar la barra 1
para eliminarlo, aplica un esfuerzo de tracción a las barras 2 y 3, alargándolas hasta
hacerlas coincidir con el extremo O´ de la barra 1. Una vez acopladas las tres barras en
O´, libera a las barras 2 y 3 del esfuerzo a las que la sometió. Como consecuencia de
ello, las barras 2 y 3 que estaban alargadas, tratarán de acortarse y arrastrarán con ellas a
la barra1 comprimiéndola. Finalmente tendremos las tres barras acopladas en el punto
O´´.
2 1 3
α α L
O
∆L
Fig. 4.22 O´
15

90. Tema 4: Tracción - Compresión
Así pues, debido al montaje se han introducido esfuerzos (tensiones) en las tres barras.
Planteemos el cálculo de los valores de esos esfuerzos:
Establezcamos el equilibrio de fuerzas de las tres barras en el punto O´´:
α
α
F2 F3
O´´
F1
Observación: al ser las deformaciones pequeñas se supondrá que el ángulo que forman
las barras inclinadas 2 y 3, al quedar unidas en O´´, es ≅ α.
Ecuaciones de equilibrio:
∑F x =0 F2 .senα = F3 .senα
(4.24)
∑F y =0 F1 = F2 .cos α + F3 .cos α
Incógnitas: F1, F2, F3
¡ Es un CASO HIPERESTÁTICO ! , tiene barras de más. Se añadirá una ecuación de
deformación
La ecuación de deformación a plantear será una que relacione el alargamiento de las
barras 2 y 3 con el acortamiento de la 1. Para ello en la siguiente figura se ha ampliado
el detalle de las uniones de las barras.
≅α ≅α
L
L
O
δ ∆L
O´´
∆L3 ∆L1
Fig. 4.23 O´
de la figura se pueden obtener las siguientes relaciones:
L
F3 .
cos α
δ + ∆L1 = ∆L ∆L3 E. A + F1.L = ∆L
→ + ∆L1 = ∆L → (4.25)
∆L3 = δ . cos α cos α cos α E. A
resolviendo el sistema formado por las ecuaciones: (4.24) y (4.25), se obtendrán: F1, F2,
F3
y dividiendo por las áreas de las secciones de las barras, se obtendrían: σ1, σ2, σ3
16

91. Sección 4.5: Recipientes a presión
Conclusiones: A las tensiones que estarán sometidas las barras de la estructura cuando
tengan que soportar una carga determinada, se le añadirán estas tensiones debidas al
montaje y como normalmente éstas no estaban previstas en el dimensionamiento de las
barras por el proyectista de las mismas, la estructura podría llegar a fallar.
4.5.-RECIPIENTES A PRESIÓN
Las formas más comunes de los recipientes a presión para contener líquidos o gases a
presión en su interior, son las esfericas y las cilíndricas.
Distinción entre recipientes a presión de pared delgada y de pared gruesa:
e e = espesor
re = radio exterior
ri = radio interior
re rm = radio medio = ( re + ri ) / 2
r = radio en una posición cualquiera
r rm
ri
PARED DELGADA: rm ≥ 10.e
PARED GRUESA: rm ≤ 10.e
Fig. 4.24
RECIPIENTES A PRESIÓN DE PARED DELGADA :
Dado que el espesor e de la pared es pequeño en relación con el radio, la pared del
depósito se comportará como si fuese una membrana y no tendrá resistencia a la flexión.
Las tensiones están distribuidas uniformemente a través del espesor de la pared y no
tienen componente radial.
Recipientes esféricos de pared delgada:
Debido a la presión interior p, un elemento de esfera estará sometido a las tensiones σ2
indicadas en la figura. Dada la simetría de la esfera las tensiones serán uniformes a lo
largo de toda ella
σ2
σ2
σ2 σ2 = tensión anular
p = presión interior
σ2
Fig. 4.25
17

92. Tema 4: Tracción - Compresión
Seccionando la esfera por la mitad y planteando el equilibrio de fuerzas de una de las
dos partes seccionadas, se tendrá:
e
σ2
σ2
x p=presión rm
rm
σ2
Fig. 4.26
Área proyectada sobre la
que actúa p
p.rm
∑F x =0 σ 2 .2.π .rm .e = p.π .rm
2
→ σ2 = (4.26)
2.e
Recipientes cilíndricos de pared delgada:
σ2
σ1 σ1 = tensión longitudinal
σ1 σ2 = tensión anular
p = presión interior
σ2
Fig. 4.27
Debido a la presión p en el interior del cilindro, un elemento de cilindro estará sometido
a las tensiones σ1 y σ2 indicadas en la figura.
Seccionando transversalmente el cilindro y planteando el equilibrio de una de las partes
seccionadas, se tendrá:
e
σ1
rm
p x
Área sobre la que se
Fig. 4.28 proyecta p
p.rm
∑F x =0 σ 1.2.π .rm .e = p.π .rm
2
→ σ1 =
2.e
(4.27)
18

93. Sección 4.5: Recipientes a presión
Seccionando ahora longitudinalmente el cilindro y estudiando el equilibrio de una de las
partes:
y
e
2.rm
p
σ2
L L
Fig. 4.29 Área proyectada sobre la que actúa p
p.rm
∑F y =0 σ 2 .2.L.e = p.2.rm .L → σ2 =
e
(4.28)
RECIPIENTES A PRESIÓN DE PARED GRUESA :
En este caso, al ser mayor el espesor de la pared del depósito, no se podrá asimilarlo a
una membrana y las tensiones tendrán ahora también componente radial y no serán
uniformes a lo largo del espesor de la pared
Para este caso nos limitaremos a expresar las fórmulas de cálculo sin su demostración.
Recipientes esféricos de pared gruesa:
σ2
σ2 σ2 = tensión anular
σ2 σ3 = tensión radial
σ3 p = presión interior
σ2
Fig. 4.30
Debido a la presión en el interior de la esfera, un elemento de ésta estará sometido a las
tensiones σ2 y σ3 indicadas, tensiones que ahora no serán uniformes a lo largo del
espesor de la pared. Sus valores son:
19

94. Tema 4: Tracción - Compresión
Tensión para una posición r cualquiera Tensión máxima
p.( re3 + 2.ri3 )
p.r 3 .( r 3 + 2 .r 3 ) σ 2 MAX =
σ2 = i 3 e 3 3 2.( re3 − ri3 )
2.r .( re − ri )
(se dará en los puntos de la superficie interior)
− p.ri3 .( re3 − r 3 ) σ 3 MAX = − p
σ3 = (4.29)
(4.30)
r 3 .( re3 − ri 3 )
(se dará en los puntos de la superficie interior)
Recipientes cilíndricos de pared gruesa:
σ2
σ1 = tensión longitudinal
σ1 σ1 σ2 = tensión anular
σ3 = tensión radial
σ3 p = presión interior
σ2
Fig. 4.31
Tensión para una posición r cualquiera Tensión máxima
p.ri 2 p.ri 2
σ1 = σ 1MAX =
re2 − ri 2 re2 − ri 2
(uniforme en todos los puntos de la pared)
p.ri 2 .( re2 + r 2 ) p.( re2 + ri 2 )
σ2 = σ 2 MAX =
r 2 .( re2 − ri 2 ) re2 − ri 2
(se dará en los puntos de la superficie interior)
− p.ri 2 .( re2 − r 2 ) σ 3 MAX = − p
σ3 = (4.31) (4.32)
r 2 .( re2 − ri 2 )
(se dará en los puntos de la superficie interior)
20

95. Sección 4.6:Introducción al dimensionamiento a resistencia de elementos metálicos a tracción-
compresión
4.6.-INTRODUCCIÓN AL DIMENSIONAMIENTO A RESISTENCIA DE
ELEMENTOS METÁLICOS SOLICITADOS A TRACCIÓN-COMPRESIÓN
(Normativa DB-SE-A)
El propósito de esta asignatura tal y como indicamos en el tema de Introducción, es la
de dar unos conocimientos base para poder calcular las tensiones y deformaciones que
se producen en el interior de los cuerpos al someterlos a cargas externas. Todo ello con
el propósito de posteriormente poder diseñar y dimensionar los diversos elementos
correspondientes a las Estructuras metálicas, de hormigón o de otros materiales, lo que
corresponderá a otras asignaturas.
No obstante y con el objetivo de poder dar una aplicación directa a los conocimientos
que se van adquiriendo en esta asignatura, se indicarán los aspectos más generales, de
forma simplificada y sin entrar en muchos detalles y casuísticas, del dimensionamiento
a resistencia de elementos metálicos sometidas a tracción-compresión, según lo
indicado en la Normativa española: CTE-DB-SE-A. (Para más detalles de este
dimensionamiento ver la citada Normativa).
Para el dimensionamiento a resistencia de elementos metálicos habrá que hacer varias
comprobaciones: unas relativas a las secciones de las piezas y otras relativas a las
propias barras.
RESISTENCIA DE LAS SECCIONES A TRACCIÓN-COMPRESIÓN
En la sección 3.2 se indicaron los criterios a utilizar para los dimensionamientos elástico
y plásticos. En esta sección los aplicaremos al caso de la Tracción-Compresión
1.-Criterio elástico de dimensionamiento:
Este criterio no se podrá aplicar al caso de la Tracción-Compresión, dado que en este
tipo de solicitaciones, al tener todos los puntos de la sección la misma tensión, todos
llegarán a la vez a alcanzar la tensión del límite elástico fy.
2.-Criterio plástico de dimensionamiento:
Consideremos una sección en la que todos sus puntos hayan alcanzado la tensión del
límite elástico (ver fig. 4.32)
σx= fyd z
A σx = fyd = cte
x
G
Npl,d = A.fyd
σx= fyd
σx= fyd
y Fig. 4.32
Observación: Se ha tomado la tensión del límite elástico, ya minorada: fyd (sección 3.6.
ecuación 3.15)
21

96. Tema 4: Tracción - Compresión
Se denomina resistencia plástica de una sección a tracción o compresión: (Npl,d) al
valor:
Npl,d = A.fyd (4.33)
Así pues para la comprobación a resistencia de una sección trabajando a tracción, se
aplicará la fórmula:
N * ≤ N pl , d = A. f yd (4.34)
siendo:
N* = N.γ (ver sección 3.6, ecuación 3.17). El valor de N se obtendrá del diagrama de
esfuerzos
Npl,d = A.fyd la resistencia plástica de la sección para el cálculo
3.-Criterio de Von Mises de dimensionamiento:
Si aplicásemos el criterio de dimensionamiento de Von-Mises (sección 3.7), llegaríamos
al mismo resultado.
En efecto, la ecuación (3.26) de Von Mises es: σ x + σ *2 − σ x .σ * + 3.τ xy ≤ f yd
*2
y
*
y
*2
N*
siendo : σ x =
*
σ * = σ z* = 0
y τ* = 0 y sustituyendo
A
N*
≤ f yd o lo que es lo mismo → N * ≤ A. f yd
A
la misma expresion del criterio plástico de dimensionamiento
RESISTENCIA DE LAS BARRAS A TRACCIÓN-COMPRESIÓN
La resistencia de las barras a tracción o compresión serán las mismas que las de sus
secciones, es decir la resistencia plástica de su sección: Npl,d.
No obstante si la barra estuviese trabajando a compresión, habría que estudiar además
su posible inestabilidad o “pandeo”, lo que estudiaremos en el tema nº 10 de esta
asignatura.
22

97. Tema 5: Flexión: Tensiones
Tema 5 : FLEXIÓN: TENSIONES
σMAX(COMPRESIÓN)
z
G n x
n
σMAX(TRACCIÓN)
y
1

98. Tema 5: Flexión: Tensiones
5.1.- INTRODUCCIÓN
Una barra está solicitada a FLEXIÓN PURA cuando en sus secciones rectas
transversales actúan únicamente los momentos flectores: Mz y/o My. (Fig. 5.1.a)
En el caso de que a la vez que los momentos flectores Mz y/o My actúen también las
fuerzas cortantes Vy y/o Vz, se dice que está solicitada a FLEXIÓN SIMPLE.(Fig.
5.1.b)
z
Vz
z
Mz G Mz x
G x
My My
y
Vy
Fig.5.1.a Fig.5.1.b y
FLEXIÓN PURA FLEXIÓN SIMPLE
Si sólo actuase uno de los dos momentos flectores: Mz o My se denomina: FLEXIÓN
SIMÉTRICA (Fig. 5.1.c)
Si el vector momento tiene las dos componentes: Mz y My se denomina: FLEXIÓN
ASIMÉTRICA (Fig. 5.1.d)
z z
Mz Mz
G x G x
My
y y
Fig.5.1.c Fig.5.1.d
FLEXIÓN SIMÉTRICA FLEXIÓN ASIMÉTRICA
2

99. Sección 5.2: Fuerzas Cortantes y Momentos Flectores. Diagramas y relaciones entre ambos
5.2.-FUERZAS CORTANTES Y MOMENTOS FLECTORES. DIAGRAMAS Y
RELACIONES ENTRE AMBOS
Ejes de referencia
z
x n<0 n>0x
O
y
Fig.5.2
Sección con normal exterior positiva: n > 0
Sección con normal exterior negativa: n < 0
Convenio de signos para las fuerzas cortantes Vy , Vz
En una sección con normal exterior positiva (n > 0), las fuerzas cortantes Vy y Vz son
positivas, cuando llevan el mismo sentido de los semiejes positivos OY, OZ
respectivamente. Serán negativas en caso contrario.
En el caso de una sección con normal exterior negativa (n < 0) será al revés
Vy
z Vz
O n<0 n>0 x
Vz
y Vy
Fig.5.3
Vy > 0 Vz > 0
3

100. Tema 5: Flexión: Tensiones
Convenio de signos para los momentos flectores Mz , My
Caso del momento flector Mz:
En una sección con normal exterior positiva (n > 0), el momento flector Mz será
positivo, cuando lleve el sentido contrario al del semieje OZ positivo . Será negativo en
caso contrario.
En el caso de una sección con normal exterior negativa (n < 0) será al revés
Mz
z
O n<0 n>0 x Mz > 0
Mz Fig.5.4
y
Mz > 0 : la viga flexa (se dobla) hacia la parte positiva del eje y
x
+
y
Fig.5.5.a
Mz < 0 : la viga flexa (se dobla) hacia la parte negativa del eje y
-
x
y Fig.5.5.b
4

102. Sección 5.2: Fuerzas Cortantes y Momentos Flectores. Diagramas y relaciones entre ellos
Caso del momento flector My:
En una sección con normal exterior positiva (n > 0), el momento flector My será
positivo, cuando lleve el mismo sentido al del semieje OY positivo . Será negativo en
caso contrario.
En el caso de una sección con normal exterior negativa (n < 0) será al revés
My
z
O n<0 n>0 x
My
y Fig.5.6
My > 0 : la viga flexa (se dobla) hacia la parte positiva del eje z
z
+
x
y Fig.5.7.a
My < 0 : la viga flexa (se dobla) hacia la parte negativa del eje z
z
- x
y
Fig.5.7.b
5

103. Tema 5: Flexión: Tensiones
Observación: El Mz es el único, que en las secciones n>o, se toma positivo si su sentido
es el contrario al semieje positivo correspondiente.
Diagramas de Fuerzas Cortantes y de Momentos Flectores
Éstos diagramas representarán las Fuerzas Cortantes y los Momentos Flectores en cada
una de las secciones de una viga, (al igual que en la sección 4.2 se estudiaron los
Diagramas de Fuerzas Normales) y gracias a ellos se podrán conocer los esfuerzos
máximos y las secciones donde éstos se darán.
Se desarrollarán los Diagramas de Fuerzas Cortantes y de Momentos Flectores a través
del siguiente ejemplo:
F z
O x
P
x
L
y
Fig.5.8
En una sección x cualquiera la Resultante y el Momento resultante de las fuerzas
exteriores serán:
F z
F.x
F
n>0
O
x
P P
P.x
x
y
Rext, Mext Fig.5.9.a
Con lo cual, la Resultante y el Momento resultante de las fuerzas interiores serán:
F z
F.x
F
n>0
O
P x
P
P.x
x
y
Rint, Mint Fig.5.9.b
6

105. Sección 5.2: Fuerzas Cortantes y Momentos Flectores: Diagramas y relaciones entre ellos
F z F z
F.x
F
x n>0
O O
P x
P P
P.x
x x
L
y y
Rint, Mint
Fig.5.10
Teniendo en cuenta elsigno de las Fuerzas Cortantes y Momentos Flectores:
F
- 0≤ x≤L
x V y = − F (cte)
Vy
Vz = − P (cte)
P
- M y = − P.x
x x =0→ My =0
Vz x = L → M y = − P.L
P.L M z = − F .x
-
x x = 0 → Mz = 0
x = L → M z = − F .L
My
F.L
-
x
Mz
7

107. Tema 5: Flexión: Tensiones
Relaciones entre Fuerzas Cortantes y Momentos Flectores
Las Fuerzas Cortantes y los Momentos Flectores no son independientes sino que están
relacionados entre sí.
Antes de ver dicha relación conviene dejar claro que, en rigor, no existen fuerzas
concentradas en un punto, pues según se vio en 1.1, por el Principio de Saint Venant, se
podrán considerar concentradas las fuerzas que se transmitan a la barra a través de una
superficie pequeña en comparación con la superficie de ésta.
R
Se considera una rebanada de una viga formada por dos secciones muy próximas,
separadas dx y sobre la que actúa una carga distribuida q(x). En ambas caras de la
rebanada se sitúan las correspondientes Fuerzas Cortantes y Momentos Flectores (todos
con sentidos positivos)
q(x) Kg/m
n<0 n>0
M G M+dM
V
V+dV
dx
Fig.5.11
Estableciendo las ecuaciones de equilibrio de los esfuerzos que actúan sobre la
rebanada:
dx
∑M G =0 M + V .dx = M + dM + q.dx.
2
simplificando y despreciando infinitésimos de 2º orden frente a los de1º:
V .dx = dM → V = dM (5.1)
dx
“La Fuerza Cortante es la derivada del Momento Flector”
8

109. Sección 5.2: Fuerzas Cortantes y Momentos Flectores. Diagramas y relaciones entre ellos
∑F = 0 V = q.dx + V + dV simplificando : 0 = q.dx + dV
dV d 2 M (5.2)
−q = =
dx dx 2
“la carga q(x) es la derivada de la Fuerza Cortante o la segunda derivada del Momento
Flector”
V=0
V=0 x
V=C1
V=C1.x+C2
V=C1.x2+C2.x+C3
V
x
M=C1 M=Mmax
M=C1.x+C2
M 2 M=C1.x3+C2.x2+C3.x+C4
M=C1.x +C2.x+C3
Observación: La expresión del Momento Flector es siempre de un grado superior a la de
la Fuerza Cortante
dM
V =0 → V = = 0 → M = C1 (cte)
dx
dM
V = C1 → V = = C1 → dM = C1 .dx → M = C1 .x + C 2
dx
dM
V = C1 .x + C 2 → V = = C1 .x + C 2 → dM = ( C1 .x + C 2 ) .dx → M = C1 .x 2 + C 2 .x + C3
dx
dM
V = 0 (en 1 punto ) → V = = 0 (en 1 punto) → M max o min
dx
9

110. Tema 5: Flexión: Tensiones
5.3.-FLEXIÓN PURA
5.3.1.-TENSIONES NORMALES: CASO GENERAL
Una viga está sometida a FLEXIÓN PURA cuando en sus secciones rectas
transversales actúan únicamente los Momentos Flectores Mz y/o My
z
O G
x
y Mz
My
Fig.5.12
Las relaciones tensiones – solicitaciones vistas en la sección 1.6 serían:
N = 0 = ∫ σ x .dA V y = 0 = ∫ τ xy .dA Vz = 0 = ∫ τ xz .dA
A A A (5.3)
T = 0 = ∫ (τ xz . y − τ xy .z ).dA M y = ∫ σ x . z.dA M z = ∫ σ x . y.dA
A A A
Pero al igual que ocurría en la Tracción-Compresión éstas ecuaciones, por si solas, no
permiten calcular las tensiones originadas por los Momentos Flectores Mz y/o My.
Habrá que recurrir nuevamente a hipótesis simplificativas que han sido comprobadas
experimentalmente.
Hipótesis de Bernouilli – Navier: “ En la Flexión Pura cada sección transversal de la
viga gira alrededor de un eje, contenido en la sección, denominado Eje Neutro,
permaneciendo las secciones planas y normales a las fibras deformadas”.
Admitiremos también que la flexión se produce en régimen elástico y por tanto dentro
de los límites de validez de la Ley de Hooke, por lo que las tensiones que se originan
han de ser proporcionales a las deformaciones producidas.
10

111. Sección 5.3.1: Flexión Pura. Tensiones normales: Caso general
Al flexionar la viga, las secciones transversales giran y hacen que las fibras
longitudinales, inicialmente rectas, dejen de serlo y se curven, alargándose o
acortándose según sea su posición en el interior de la viga.
Fibras que se acortan
Fibras que se alargan
Fig.5.13
Existen fibras longitudinales que ni se alargan ni se acortan, a esas fibras se las
denomina FIBRAS NEUTRAS.
A la superficie donde se encuentran las fibras neutras se la denomina SUPERFICIE
NEUTRA. Las fibras que estén por encima o por debajo de la Superficie Neutra
alargarán o acortarán según hacia donde flexione la viga. (En el caso del dibujo
acortarán las fibras que están por encima de la Superficie Neutra y alargarán las que
estén por debajo)
A las fibras transversales de la Superficie Neutra se las denomina: LINEAS NEUTRAS
o EJES NEUTROS. Alrededor de ellos giran las secciones transversales
En las siguientes figuras se representan estos términos para su mejor identificación:
Superficie Neutra
Eje Neutro o
Fibras Neutras Ejes Neutros o
Línea Neutra
Líneas neutras
Fig.5.14
11

112. Tema 5: Flexión: Tensiones
Así pues como resultado de la flexión el paralelepípedo elemental abcd se transforma
en el a1b1c1d1 y como según la Hipótesis de Bernouilli-Navier: “……las secciones
transversales de la viga giran alrededor de un eje, contenido en la sección, denominado
Eje Neutro, permaneciendo planas y normales a las fibras deformadas”, se deducirá
que: a1b1 será perpendicular a a1c1. Con lo cual se podrá afirmar: “Las deformaciones
angulares de los diferentes paralelepípedos son nulas, es decir: γ = 0”
m n
a b m1 n1
a1 b1
c d c1
d1
dx Fig.5.15
τ
Por la ley de Hooke: γ==0 → τ =0 (5 . 4 )
G
“En la Flexión Pura son nulas las tensiones cortantes”
Para calcular las tensiones normales σx, se analizará con más detalle la deformación de
la rebanada dx de la figura anterior
O
Supongamos que la superficie
neutra es la que pasa por la
r fibra mn. (m1n1 una vez
flexionada)
O: Centro de curvatura de la
fibra neutra m1n1
r: radio de curvatura de la
m n m1 dx fibra neutra m1n1
a dn b a1 dn n1
c d c1 b2 b1
d1
dx
Se estudiará el alargamiento que ha sufrido la fibra ab que se encuentra a una distancia
dn de la superficie neutra. La fibra ab de longitud dx al flexionar se ha convertido en la
fibra a1b1.
La fibra neutra mn de longitud dx al flexionar se ha convertido en la fibra m1n1 de la
misma longitud (la fibra neutra ni alarga ni acorta). Si se traza por n1 una paralela a
m1a1 se obtiene n1b2, siendo entonces: a1b2 =dx. El alargamiento de la fibra ab al
flexionar habrá sido: b2b1. A continuación se buscará una expresión para obtener dicho
alargamiento:
bb bb
De la semejanza de ε x = 2 1 = 2 1 triángulos (Oa1b1) y (n1b2b1), tienen
12 a1b2 dx

113. Sección 5.3.1: Flexión Pura. Tensiones normales: Caso general
sus lados paralelos , se podrá expresar:
b2b1 d n
=
dx r
b2 b1 d n
Sustituyendo en la expresión de εx: = εx =
dx r
“ las deformaciones longitudinales de las fibras son proporcionales a su distancia a
la superficie neutra”
σx dn
y por la ley de Hooke: εx = → σ x = ε x .E = E . (5.5)
E r
“ las tensiones normales σx son proporcionales a su distancia a la superficie
neutra”
Utilizando ahora la primera ecuación de las expresiones (5.3) resultará:
dn E
∫σ
A
x .dA = 0 → ∫A
E.
r
.dA = 0 (al ser E=cte, r=cte) →
r ∫A
d n .dA = 0 →
→ ∫A
d n .dA = 0
Si se quisiera obtener ahora la distancia del centro de gravedad de la sección a la
superficie neutra, la fórmula a emplear sería:
d n (G ) =
∫ A
d n .dA
= (y por lo obtenido antes) =
0
=0 → d n (G ) = 0 (5 . 6 )
∫ A
dA ∫ dA
A
“la distancia del centro de gravedad G de una sección a la superficie neutra es
cero, el centro de gravedad está pues en la superficie neutra”, o lo que es lo mismo
“el eje neutro o línea neutra de una sección pasa por el centro de gravedad G de la
misma”
G
Eje Neutro o
Línea Neutra
Fig.5.16
13

114. Tema 5: Flexión: Tensiones
Se buscará a continuación una forma cómoda para medir dn, Para ello, la siguiente
figura (5.17), representa una sección transversal cualquiera de una viga y se expresará
dn en función de las coordenadas del punto donde se quiera hallar la tensión.
Línea neutra o Eje neutro
n
α
G dn
y z
z P
n
y Fig.5.17
La distancia dn de un punto P(y,z) cualquiera a la línea neutra será:
d n = y. cos α + z.senα
Introduciendo este valor en la ecuación (5.5) que da la tensión normal en un punto
cualquiera quedará:
dn E
σ x = E. = .( y. cos α + z.senα ) = C1 . y + C 2 .z (5 . 7 )
r r
Desarrollando ahora dos nuevas ecuaciones de las expresiones (5.3):
M z = ∫ σ x . y.dA = (y según 5.6) = ∫ (C1 . y + C2 .z ). y.dA
A A
= C1.∫ y .dA + C2 .∫ z. y.dA = C1 .I z + C2 .I zy
2
A A
M y = ∫ σ x .z.dA = ( y según 5.6) = ∫ (C1 . y + C2 .z ). z.dA
A A
= C1.∫ y.z.dA + C2 .∫ z .dA = C1.I zy + C2 .I y
2
A A
y resolviendo este sistema de ecuaciones por la regla de Cramer:
14

115. Sección 5.3.1: Flexión Pura. Tensiones normales: Caso general
Mz I zy Iz Mz
My Iy M z .I y − M y .I zy I zy My M y .I z − M z .I zy
C1 = = C2 = =
Iz I zy I z .I y − I 2
zy Iz I zy I z .I y − I zy
2
I zy Iy I zy Iy
Sustituyendo finalmente el valor obtenido para las dos constantes C1 y C2 en la ecuación
(5.7), quedará como expresión final general del cálculo de la tensión normal en un
punto cualquiera de coordenadas (y,z) la siguiente:
( M z .I y − M y .I zy ). y + ( M y .I z − M z .I zy ).z
σx = (5.8)
I z .I y − I zy
2
Las componentes del estado de tensiones en un punto P del interior de una viga
sometida a Flexión Pura serán pues:
z
σx σx x
P
y Fig.5.18
( M z .I y − M y .I zy ). y + ( M y .I z − M z .I zy ).z
σx = τ xy = 0
I z .I y − I zy
2
(5.9)
σy =0 τ yz = 0
σz = 0 τ zx = 0
15

116. Tema 5: Flexión: Tensiones
CÁLCULO DE LA LÍNEA NEUTRA (EJE NEUTRO)
Las fibras que pertenecen a la Superficie Neutra, por definición, ni se alargan ni se
acortan, con lo cual se cumplirá:
ε x = 0 y por la ley de Hooke : σ x = ε x .E = 0
Así pues la ecuación de la línea neutra la podemos obtener como lugar geométrico de
los puntos de una sección que tienen tensión normal cero, es decir:
( M z .I y − M y .I zy ). y + ( M y .I z − M z .I zy ).z
σx = =0
I z .I y − I zy
2
o lo que es lo mismo:
( M z .I y − M y .I zy ). y + ( M y .I z − M z .I zy ). z = 0 (5.10)
Ecuación de la línea neutra o Eje neutro
También puede expresarse, sabiendo que ha de pasar por el centro de gravedad G de la
sección, en virtud de (5.6), por su ángulo de inclinación α con respecto al eje z.
y M y .I z − M z .I zy
tagα = = (despejando esta expresion de5.10) = − (5.11)
z M z .I y − M y .I zy
Ángulo de inclinación de la línea neutra respecto al eje Z
Sección transversal de la viga
n
G
z
α
n
y Fig.5.19
16

117. Tema 5.3.2: Tensiones normales: Casos particulares
5.3.2.-TENSIONES NORMALES: CASOS PARTICULARES
Caso Particular 1º: “Los ejes y,z son los Ejes Principales de inercia de la sección”
En éste caso se deberá cumplir: Izy = 0, con lo cual las ecuaciones 5.8 y 5.11 serán:
M z . y M y .z M y .I z
σx = + (5.12) tag α = − (5.13)
Iz Iy M z .I y
Caso Particular 2º: “Los ejes y,z son los Ejes Principales de inercia de la sección y
además uno de los Momentos Flectores es cero”
Si My = 0 :
M z .y tagα = 0 → α = 0º
σx = (5.14) (5.15)
Iz el eje neutro es el eje z
La distribución de tensiones normales σx para este caso será:
σMAX(COMPRESIÓN)
z
M z . yMAX
G n x σ X max = (5.16)
Iz
n
σMAX(TRACCIÓN)
y
Fig.5.20
17

118. Tema 5 : Flexión: tensiones
Si Mz = 0 :
M y .z tagα = ∞ → α = 90º
σx = (5.17 ) (5.18)
Iy el eje neutro es el eje y
La distribución de tensiones normales σx para este caso será:
σMAX(TRACCIÓN)
n z
G x
M y .zMAX
σ X max = (5.19)
Iy
n
σMAX(COMPRESIÓN)
y
Fig.5.21
18

119. Tema 5.3.2: Tensiones normales: Casos particulares
Observaciones:
Convenio de signos para Mz y My:
Con el convenio de signos adoptado en la sección 5.2 para los Momentos flectores Mz y
My se observa lo siguiente:
Mz > 0 → “las fibras que se alargan son las que están por debajo de la superficie
neutra, por tanto se producirá TRACCIÖN en los puntos de la sección de la parte
inferior del eje z, es decir en los puntos de la parte positiva del eje y”
Mz Superficie neutra
z
Compresión
n>0 n
G n
x
n n G n z
n
Mz y
Tracción y
Fig.5.22
My > 0 → “las fibras que se alargan son las que están en la parte positiva del eje z”
Superficie neutra
My Tracción
z
n n n
x
n>0 G z
n n
n
My Compresión y
y
Fig.5.23
19

120. Tema 5 : Flexión: tensiones
5.3.3.-LÍNEA ELÁSTICA. RADIO DE CURVATURA
Se denomina LÍNEA ELÁSTICA al eje x de la viga una vez deformado debido a la
flexión.
Línea elástica
x
x
Fig.5.24
El radio de curvatura de la línea elástica se podrá obtener de la siguiente manera:
dn
La ecuación 5.5 que daba la tensión en un punto P cualquiera: σ x = E.
r
n
α
G dn n G n
y z dn = y z
z P P
n
y Fig.5.25 y
y para el 2º caso particular visto en 5.3.2: ( Izy = 0 My = 0 ) → el eje neutro es el eje z
y
Entonces : dn = y, con lo cual la fórmula de la tensión será: σ x = E.
r
M z .y
La fórmula final (5.14), para el cálculo de la tensión en éste caso particular era: σx =
Iz
Igualando ambas expresiones de la tensión:
E. y M z . y 1 Mz
= → = (5.20)
r Iz r E .I z
Siendo: E.Iz = Módulo de Rigidez a la flexión alrededor del eje z.
1
así si: E.I z ↑ → ↓ → r ↑ ⇒ flexa poco,es muy rígida a la flexión
r
20

121. Sección 5.3.3: Línea elástica. Radio de curvatura
E.Iz (grande) E.Iz (pequeño)
⇓ ⇓
Flexiona poco Flexiona mucho
⇓ ⇓
muy rígida a la flexión poco rígida a la flexión
Para el otro caso particular visto en 5.3.2: ( Izy = 0, Mz = 0 ) → el eje neutro es el eje
y, entonces dn = z.
n
G
z
dn = z
P
n y Fig.5.26
z
Con lo cual la ecuación (5.5) para la tensión sería: σ x = E.
r
La ecuación final (5.17), para el cálculo de la tensión en éste caso particular era:
M y .z
σx =
Iy
Igualando ambas expresiones de la tensión:
E. z M y . z 1 My
= → = (5.21)
r Iy r E .I y
Siendo: E.Iy = Módulo de Rigidez a la flexión alrededor del eje y.
21

122. Tema 5: Flexión: Tensiones
5.4.-FLEXIÓN SIMPLE
Una viga está solicitada a FLEXIÓN SIMPLE cuando en sus secciones transversales actúan
conjuntamente los Momentos Flectores: Mz y/o My y las Fuerzas Cortantes: Vy y/o Vz.
z
Vz
O G x
Mz
My
y
Fig.5.27 Vy
Las relaciones Tensiones – Solicitaciones vistas en 1.7 serían:
N = 0 = ∫ σ x .dA V y = ∫ τ xy .dA Vz = ∫ τ xz .dA
A A A (5.22)
T = 0 = ∫ (τ xz . y − τ xy .z ).dA M y = ∫ σ x . z.dA M z = ∫ σ x . y.dA
A A A
5.4.1-TENSIONES NORMALES
En estas ecuaciones (5.22), se observa que en las relaciones que interviene la tensión normal
σx, son las mismas que las expresadas en las (5.3) para la Flexión Pura. Sin embargo la
aparición ahora de las tensiones cortantes: τxy y τxz , que eran cero en la Flexión Pura, va a
producir deformaciones angulares γ, que habrá que añadir a las deformaciones propias de la
Flexión Pura.
Si las tensiones cortantes no se distribuyeran uniformemente en la sección, lo mismo ocurriría
con las deformaciones angulares, lo que significará que en la FLEXIÓN SIMPLE las
secciones planas se alabean, es decir, no permanecerán planas y no se cumplirá por tanto la
Hipótesis de Bernouilli- Navier
Fibras que se acortan
Fibras que se alargan
Fig.5.28
22

123. Sección 5.4.1: Flexión simple: tensiones normales
Sin embargo se comprueba, que este alabeo de las secciones apenas influye en el valor de las
tensiones normales σx, con lo cual se aplicará para éstas, en el caso de FLEXIÓN SIMPLE,
las mismas ecuaciones obtenidas en la FLEXIÓN PURA, es decir:
( M z .I y − M y .I zy ). y + ( M y .I z − M z .I zy ).z
σx =
I z .I y − I zy
2
(5.7)
σy =0
σz = 0
Caso Particular 1º:
“Los ejes y,z son los Ejes Principales de inercia de la sección”
En éste caso se deberá cumplir: Izy = 0, con lo cual las ecuaciones 5.7 y 5.10 serán:
M z . y M y .z M y .I z
σx = + (5.12) tag α = − (5.13)
Iz Iy M z .I y
Caso Particular 2º:
“Los ejes y,z son los Ejes Principales de inercia de la sección y además uno de los Momentos
Flectores es cero”
Si My = 0 :
M z .y tagα = 0 → α = 0º
σx = (5.14)
(5.15)
Iz el eje neutro es el eje z
23

124. Tema 5: Flexión: Tensiones
5.4.2-TENSIONES CORTANTES EN SECCIONES DE GRAN ESPESOR
Para el cálculo de las tensiones cortantes se tendrá en cuenta la forma de la sección de la viga.
Así en este apartado se comenzará con el caso de vigas con secciones de gran espesor:
circulares, rectangulares, etc…..
En este tipo de secciones se hará el cálculo por separado de las tensiones cortantes: τxy y τxz.
Cálculo de la tensión cortante τxy:
Tomemos una rebanada dx de una viga de sección de gran espesor sometida a Flexión Simple
(Fig.29.a). En ambos extremos de la misma se sitúan los Momentos Flectores y Fuerzas
Cortantes correspondientes. Se trata de calcular las τxy en los puntos de una línea cualquiera
ab que se encuentran a una distancia y del eje z. Para ello se supondrá que τxy = cte a lo largo
de todos los puntos de la dicha línea.
Vy
z Vz + dVz
My
Mz
n<0 O G x
b n>0 c
y Mz + dMz
Vz
a d
My + dMy
τxy
y
Vy + dVy
dx
Fig.5.29.a
Seccionando el elemento diferencial por el plano abcd y estableciendo el equilibrio de fuerzas
del trozo inferior resultante, se tendrá:
dx
t(y)
b c A
τyx
a
σx d
dA dA σx +dσx
Fig.29.b
Mz, My →σx M z + dM z , M y + dM y → σ x + dσ x
y para que exista equilibrio de fuerzas en direccion del eje x → τ yx sobre superficie abcd
∑F x =0 → ∫ (σ
A
x + dσ x ).dA = ∫ σ x .dA + τ yx .t ( y ).dx
A
y operando :
24

125. Sección 5.4.2: Tensiones cortantes en secciones de gran espesor
dσ x
∫ dσ x .dA = τ yx .t ( y ).dx → ∫ .dA = τ yx .t ( y) (1)
A A dx
dσ x
Calculemos a partir de la expresión de σ x obtenida en (5.7) :
dx
( M z .I y − M y .I zy ). y + ( M y .I z − M z .I zy ).z M z .( I y . y − I zy .z ) + M y .( I z .z − I zy . y )
σx = =
I z .I y − I 2
zy I z .I y − I zy
2
. ( I y . y − I zy .z ) + . ( I z .z − I zy . y ) V .( I . y − I .z ) + V .( I .z − I . y )
dM z dM y
dσ x dx dx
= =
y y zy z z zy
dx I z .I y − I zy
2
I z .I y − I zy
2
y sustituyendo esta expresión en (1):
Vy . ( I y . y − I zy .z ) + Vz . ( I z .z − I zy . y )
τ yx .t ( y ) = ∫ .dA
A I z .I y − I zy
2
Vy .  I y .∫ y.dA −I zy .∫ z.dA + Vz .  I z .∫ z.dA − I zy .∫ y.dA
τ yx .t ( y ) =  A A   A A 
I z .I y − I zy
2
Vy .  I y .Qz ( y ) − I zy .Qy ( y )  + Vz .  I z .Qy ( y ) − I zy .Qz ( y ) 
   
τ yx =
t ( y ).  I z .I y − I zy 

2

y como por lo visto en el tema 1º : τyx = τxy se obtendrá finalmente:
Vy .  I y .Qz ( y ) − I zy .Qy ( y )  + Vz .  I z .Q y ( y ) − I zy .Qz ( y ) 
   
τ xy = (5.23)
t ( y ).  I z .I y − I zy 

2

siendo:
Qz ( y) = ∫ y.dA
A
Q y ( y ) = ∫ z.dA
A
G z los momentos estáticos del área rayada A
y respecto de los ejes z e y respectivamente
a b
Observación: en la sección de n>0 se cumple:
τxy>0 A
y
τ xy > 0 → "su sentido es entrante en el área rayada "
t(y) Fig.5.30 τ xy < 0 → "su sentido es saliente del área rayada "
25

126. Sección 4.5.2: Tensiones cortantes en secciones de gran espesor
Cálculo de la tensión cortante τxz:
Se trata de calcular ahora las τxz en los puntos de una línea cualquiera ef que se encuentran a
una distancia z del eje y. Para ello se supondrá que τxz = cte a lo largo de todos los puntos de
la dicha línea.
Vy
Vz + dVz
f z
g
My
Mz
n<0 O G x
n>0
τxz Mz + dMz
Vz z
e h
My + dMy
y
Vy + dVy
dx Fig.5.31.a
Seccionando el elemento diferencial por el plano efgh y estableciendo el equilibrio de fuerzas
del trozo posterior resultante, se tendrá:
f g
σx dA τzx dA σx + dσx
t(z)
A
e h
dx Fig.5.31.b
Mz, My →σx M z + dM z , M y + dM y → σ x + dσ x
y para que exista equilibrio de fuerzas en direccion del eje x → τ zx sobre superficie efgh
∑F x =0 → ∫ (σA
x + dσ x ).dA = ∫ σ x .dA + τ zx .t ( z ).dx
A
y operando:
dσ x
∫ dσ x .dA = τ zx .b( z ).dx .dA = τ zx .t ( z )
→ ∫
A A dx
ysiguiendo un procesosimilar al anterior,se obtendrá:
Vy .  I y .Qz ( z ) − I zy .Qy ( z )  + Vz .  I z .Qy ( z ) − I zy .Qz ( z ) 
   
τ xz = (5.24)
t ( z ).  I z .I y − I zy 

2

26

128. Sección 5.4.2: Tensiones cortantes en secciones de gran espesor
siendo:
f
τxz>0 Qz ( z) = ∫ y.dA Q y ( z ) = ∫ z.dA
A A
t(z)
G A los momentos estáticos del área rayada A
z
respecto de los ejes z e y respectivamente
z
Observación: en la sección de n>0 se cumple:
e
y τ xz > 0 → "su sentido es entrante en el área rayada "
Fig.5.32 τ xz < 0 → "su sentido es saliente del área rayada "
CASOS PARTICULARES:
Caso Particular 1º:
“Los ejes y,z son los Ejes Principales de inercia de la sección”
En éste caso se deberá cumplir: Izy = 0, con lo cual las ecuaciones 5.23 y 5.24 serán:
Vy .Qz ( y ) Vz .Qy ( y ) Vy .Qz ( z ) Vz .Qy ( z )
τ xy = + τ xz = + (5.25)
t ( y ).I z t ( y ).I y t ( z ).I z t ( z ).I y
Caso Particular 2º:
“Los ejes y,z son los Ejes Principales de inercia de la sección y además una de las Fuerzas
Cortantes es cero”
Vy .Qz ( y ) Vy .Qz ( z )
-si Vz = 0 → τ xy = τ xz = (5.26)
t ( y ).I z t ( z ).I z
Vz .Qy ( y ) Vz .Qy ( z )
- si Vy = 0 → τ xy = τ xz = (5.27)
t ( y ).I y t ( z ).I y
27

130. Tema 5: Flexión: Tensiones
5.4.3-TENSIONES CORTANTES EN SECCIONES ABIERTAS DE PEQUEÑO
ESPESOR
Las barras que se utilizan en las estructuras metálicas suelen tener secciones de pequeño
espesor.
tf tf
tw
h tw h
d d
b b
Fig.5.33
Se consideran incluidas en este grupo todas las secciones en las que se cumpla:
h ≥ 10.tw b ≥ 10.t f
El cálculo de las tensiones cortantes en este tipo de secciones, presenta algunas diferencias
con respecto al de las secciones macizas visto anteriormente.
Cálculo de la tensión cortante τxs:
Tomemos una rebanada dx de una viga de sección abierta de pequeño espesor sometida a
Flexión Simple. En ambos extremos de la misma se sitúan los Momentos Flectores y Fuerzas
Cortantes correspondientes. Se trata de calcular las τxs en los puntos de una línea cualquiera
ab, perpendicular a la línea media, que se encuentran a una distancia s de uno de los extremos
abiertos de la sección. Para ello se supondrá que τxs = cte a lo largo de todos los puntos de
dicha línea y sus direcciones son perpendiculares a la misma
Vy dx
My
z
Vz+dVz
Mz
G n>0 x
n<0 Vz
τxs b c
Mz+dMz
a
My+dMy
s y
Vy+dVy Fig.5.34.a
28

132. Sección 5.4.3: Tensiones cortantes en secciones abiertas de pequeño espesor
Seccionando el elemento diferencial por el plano abcd y estableciendo el equilibrio de fuerzas
en dirección del eje x, del trozo inferior resultante, se tendrá:
t(s)
b τsx c
a d
σx+dσx
σx dA
s
dx Fig.5.34.b
∑F x =0 → ∫ (σ
A x + dσ x ).dA = ∫ σ x .dA + τ sx .t ( s ).dx
A
y operando:
dσ x
∫ dσ x .dA = τ sx .t ( s).dx → ∫ .dA = τ sx .t ( s)
A A dx
y siguiendo a partir de ahora un desarrollo similar al realizado en el cálculo de las tensiones
cortantes en secciones de gran espesor, se obtendrá:
Vy .  I y .Qz ( s ) − I zy .Qy ( s )  + Vz .  I z .Qy ( s ) − I zy .Qz ( s ) 
   
τ xs = (5.28)
t ( s ).  I z .I y − I zy 

2

siendo:
G z Q z (s) = ∫ y.dA
A
Q y ( s ) = ∫ z.dA
A
b los momentos estáticos del área rayada A
a τxs>0
respecto de los ejes z e y respectivamente
A
s Observación: en la sección de n>0 se cumple:
y
τ xs > 0 → "su sentido es entrante en el área rayada "
Fig.5.34.c τ xs < 0 → "su sentido es saliente del área rayada "
29

134. Tema 5: Flexión: Tensiones
CASOS PARTICULARES:
Caso Particular 1º:
“Los ejes y,z son los Ejes Principales de inercia de la sección”
En éste caso se deberá cumplir: Izy = 0, con lo cual la ecuación 5.28 será:
Vy .Qz ( s ) Vz .Qy ( s )
τ xs = + (5.29)
t ( s ).I z t ( s ).I y
Caso Particular 2º:
“Los ejes y,z son los Ejes Principales de inercia de la sección y además una de las Fuerzas
Cortantes es cero”
Vy .Qz ( s )
-si Vz = 0 → τ xs = (5.30)
t ( s ).I z
Vz .Q y ( s )
- si Vy = 0 → τ xs = (5.31)
t ( s ).I y
30

135. Sección 5.4.4: Tensiones cortantes en secciones cerradas de pequeño espesor
5.4.4-TENSIONES CORTANTES EN SECCIONES CERRADAS DE PEQUEÑO
ESPESOR
Cálculo de la tensión cortante τxs:
Tomemos una rebanada dx de una viga de sección cerrada de pequeño espesor sometida a
Flexión Simple. En ambos extremos de la misma se sitúan los Momentos Flectores y Fuerzas
Cortantes correspondientes. Se trata de calcular las τxs en los puntos de una línea cualquiera
ab, perpendicular a la línea media, que se encuentran a una distancia s de una línea aobo,
también perpendicular a la línea media, que se tomará como referencia. Para ello se supondrá
que τxs = cte a lo largo de todos los puntos de la línea ab, de espesor t(s), siendo sus
direcciones perpendiculares a la misma y que igualmente ocurrirá con las tensiones τxso = cte
en los puntos de la línea de referencia aob, de espesor t(so)
Vy
dx
My
z
Mz Vz+dVz
n<0 G n>0 x
τxs b Mz+dMz
a Vz
Vy+dVy
b0
s τxso a0
My+dMy
y
Fig.5.35.a
Seccionando el elemento diferencial por el plano abcd y por el aobocodo, y estableciendo el
equilibrio de fuerzas en dirección del eje x, del trozo resultante, se tendrá:
t(s)
b τsx c
a
dA
d σx+dσx
σx b0 τsox co
t(so)
s a0 do
dx
Fig.5.35.b
∑F x =0 → ∫ (σ
A x + dσ x ).dA + τ sox .t ( so ).dx = ∫ σ x .dA + τ sx .t ( s ).dx
A
dσ x
∫ dσ x ..dA + τ sox .t ( so ).dx = τ sx .t ( s ).dx → ∫ ..dA + τ sox .e( s o ) = τ sx .e( s )
A A dx
dσ x
y sustituyendo el valor de ∫A dx
.dA obtenido en la sección 5.4.3:
31

136. Tema 5: Flexión: Tensiones
Vy .  I y .Qz ( s) − I zy .Qy ( s )  + Vz .  I z .Qy ( s) − I zy .Qz ( s ) 
   
τ sx .t ( s ) = τ sox .t ( so ) + (5.32)
I z .I y − I zy
2
Observación: en esta expresión se observa que para poder calcular τsx se deberá antes conocer
τsox. Ésto no ocurría en las secciones abiertas de pequeño espesor, pues en ellas tan sólo era
necesario dar un corte para aislar el elemento diferencial y estudiar sobre él, el equilibrio de
fuerzas, con lo cual se obtenía una ecuación con una sola incógnita: τsx, y se la podía calcular
directamente.
Cálculo de una tensión de referencia: τsox
El cálculo de una tensión de referencia τsox se obtiene a partir de la siguiente propiedad: “la
suma de las deformaciones angulares γxs a lo largo de toda la línea media de una sección
cerrada de pequeño espesor es cero”
s s
τ xs
∫ γ xs .ds = 0
0
y por la ley de Hooke : → ∫ G .ds = 0
0
y sustituyendo τxs =τsx por su valor obtenido de la ecuación (5.32):
s
τ sox .t ( so ) s
V y .  I y .Qz ( s ) − I zy .Q y ( s )  + Vz .  I z .Q y ( s ) − I zy .Qz ( s ) 
   
∫
0
t ( s ).G
.ds + ∫
0
t ( s ).G.( I y .I z − I zy )
2
.ds = 0
como : τ sox = cte, t ( so ) = cte y eliminando G :
s
ds
s
V y .  I y .Qz ( s ) − I zy .Q y ( s )  + Vz .  I z .Q y ( s ) − I zy .Qz ( s ) 
    .ds = 0
τ sox .t ( so ).∫ +∫
0
t (s) 0 t ( s ).( I y .I z − I zy )
2
y despejando finalmente τ sox :
 s Q ( s) s
Q ( s)   s Q (s) s
Q (s) 
Vy .  I y .∫ z .ds − I zy .∫ y .ds  + Vz .  I z .∫ y .ds − I zy .∫ z .ds 
t ( s) t ( s)  0 t (s) t (s)
−  0 0  0 
(5.33)
t ( s0 ).( I z .I y − I zy )
2
τ sox = s
= τ xso
ds
∫ t (s)
0
32

137. Sección 5.4.4: Tensiones cortantes en secciones cerradas de pequeño espesor
Una vez obtenida de esta forma τsox, sustituyendo su valor en la ecuación (5.33) se obtendría
el valor de la tensión que se quería calcular: τxs = τsx
τ xso .t ( s0 ) Vy .  I y .Qz ( s ) − I zy .Qy ( s )  + Vz .  I z .Qy ( s ) − I zy .Qz ( s ) 
τ xs = +     (5.34)
t (s) t ( s ).( I z .I y − I zy )
2
CASOS PARTICULARES:
Caso Particular 1º: “Los ejes y,z son los Ejes Principales de inercia de la sección”
En éste caso se deberá cumplir: Izy = 0, con lo cual las ecuaciones 5.33 y 5.34 serán:
s s
Qz ( s ) Q (s)
Vy .∫ .ds Vz .∫ y .ds
t (s) t ( s)
0
+ 0
t ( s0 ).I z t ( s0 ).I y (5.35)
τ xso = − s
ds
∫ t ( s)
0
τ xso .t ( s0 ) Vy .Qz ( s ) Vz .Qy ( s )
τ xs = + + (5.36)
t (s) t ( s ).I z t ( s ).I y
Caso Particular 2º: “Los ejes y,z son los Ejes Principales de inercia de la sección y además
una de las Fuerzas Cortantes es cero”
Por ejemplo: caso de Vz = 0
s
Qz ( s )
Vy .∫ .ds
t ( s)
τ xso .t ( s0 ) Vy .Qz ( s )
0
t ( s0 ).I z (5.37) τ xs = + (5.38)
τ xso = − s t (s) t ( s ).I z
ds
∫ t (s)
0
Caso Particular 3º:
33

138. Tema 5: Flexión: Tensiones
“Si el eje y es de simetría y sólo hay Vy”
τxso = 0
τxs
z
Vy
τxso = 0
y Fig.5.36
En este caso las ecuaciones anteriores se simplifican, pues se demuestra que en los puntos de
corte de la sección con el eje y la tensión cortante es cero.
Así pues tomando dichos puntos como referencia, en ellos será: τxso =0 (5.39)
con lo cual la tensión cortante en cualquier otros puntos será:
Vy .Qz ( s )
τ xs = (5.40)
t ( s ).I z
siendo Qz(s) el momento estático del área rayada respecto del eje z
Fórmulas análogas se obtendrían si el eje z fuese de simetría y sólo hubiese Vz
Y finalmente si ambos ejes: y, z, fuesen de simetría y hubiese Vy y Vz, las fórmulas se
obtendrían por el Principio de Superposición de los Efectos, estudiando cada caso por
separado y sumando los valores obtenidos en ambos.
34

139. Sección 5.4.5: Centro de fuerzas cortantes
5.4.5-CENTRO DE FUERZAS CORTANTES
Sea una viga con sección abierta de pequeño espesor y sea F la Resultante de las fuerzas
exteriores aplicada en el punto G de la sección indicada en la Fig. (5.37). La fuerza cortante
en dicha sección será pues: Vy = F
Vext = F
G
x z
Vy = Rint = F
y Fig.5.37
La distribución de tensiones cortantes τxs en las alas y en el alma de la sección, aplicando la
ecuación (5.30) será la indicada en la Fig. (5.38.a):
τxs = τxz
τxs = τxy G
z
Vy
τ = τxz
y xs
Fig.5.38.a
La suma de las tensiones cortantes en el alma τxs = τxy dará lugar a una resultante que será Vy,
y las de las alas: τxs = τxz, darán lugar a unas resultantes Vz. (Fig.5.38.b).
Llevando la acción de estas resultantes de las fuerzas interiores: Vy y Vz, al centro de
gravedad G de la sección, darán lugar a una Resultante: Vy (la suma de las Vz será cero, al
ser iguales, de la misma dirección, pero de sentidos contrarios), y un Momento Resultante:
Mx = Vz.h + Vy.c que produce una Torsión en la sección (Fig. 5.38.c)
Vz
Mx = Vz.h + Vy.c
G G
Vy z h ⇒ z
Vz Vy
c y y Fig.5.38.c
Fig.5.38.b.
35

140. Tema 5: Flexión: Tensiones
Este efecto inesperado de la Torsión que producen las tensiones cortantes y al que tan
sensibles son este tipo de secciones abiertas y de pequeño espesor (tienen muy poca rigidez a
la torsión), se podrá evitar si se aplican las fuerzas exteriores, en lugar de en el centro de
gravedad G de la sección, en un punto C al que llamaremos “Centro de Fuerzas Cortantes”.
Calculemos a continuación la posición del Centro de Cortantes ( C ), para la sección dada.
Para ello se situarán las fuerzas exteriores que actúen sobre la viga, de modo que la Resultante
de las mismas pase por un punto C sobre el eje z y a una distancia d del centro de gravedad G
de la sección. (Fig.5.39.a). Para ver el efecto que dicha Resultante provoca en G, la
trasladamos a dicho punto, dando lugar a una fuerza: F y un momento: F.d. (Fig. 5.39.b)
Vext = F
Vext = F
Mx = F.d
C G C G
z ⇒ z
d d
y y
Fig.5.39.a Fig.5.39.b
b
Pero al estar la Resultante de las fuerzas exteriores F, aplicada ahora en el punto G, (Fig.
5.39.b) , F, esta fuerza sólo, por lo visto anteriormente, provocará unas fuerzas internas que
daban lugar a la fuerza y al momento indicados (Figs.5.40.a y b)
Vext = F Mx = Vz.h + Vy.c
G G
x z ⇒ z
Vy = Rint = F
Ry
y Fig.5.40.b
y Fig.5.40.a
Si situamos el punto C a una distancia d del punto G, tal que se consiga que el momento
torsor exterior: Mx, sea igual y de sentido contrario al provocado por las fuerzas internas: Mx ,
se habrá conseguido anular éstas, es decir se habrá anulado el efecto de la Torsión en la
sección
Vz .h + V y .c
F.d = Vz.h + Vy.c ⇒ d= (5.41)
F
con ello queda localizada la posición del punto C (Centro de fuerzas cortantes), para este tipo
de sección
36

141. Sección 5.4.5: Centro de fuerzas cortantes
Observaciones:
Para otros tipos de secciones, los Centros de Cortantes serán:
a) Secciones abiertas de pequeño espesor con dos ejes de simetría
C≡G z
y
Fig.5.4
1
b) Secciones abiertas de pequeño espesor con sólo un eje de simetría
C G G
z z
C G
z
y
d C
y y
Fig.5.42.a Fig.5.42.b Fig.5.42.c
c) Secciones abiertas de pequeño espesor sin ejes de simetría
C≡G
z
y
Fig.5.43
37

142. Tema 5: Flexión: Tensiones
5.5-INTRODUCCIÓN AL DIMENSIONAMIENTO A RESISTENCIA DE VIGAS
METÁLICAS SOLICITADAS A FLEXIÓN ( Normativa DB-SE-A )
5.5.1.-RESISTENCIA DE LAS SECCIONES A FLEXIÓN PURA: MOMENTOS
FLECTORES
1.-Criterio elástico de dimensionamiento:
Según vimos en la sección 3.7: “La resistencia elástica de una sección se obtendrá cuando en
un punto de la misma se alcance la tensión del límite elástico fy.”
Caso de una sección solicitada por un momento flector Mz:
Al momento flector Mz que produce la tensión del límite elástico fyd en los puntos más
alejados de la línea neutra, se le denomina: Mzel,d y representa la resistencia elástica de una
sección a la flexión Mz.. Calculemos su valor:
La distribución de tensiones normales σx para este caso será, (ver fig.5.44):
σMAX(COMPRESIÓN) = fyd
z
G n x Mz = Mzel,d
n
σMAX(TRACCIÓN) = fyd
y
Fig.5.44
M zel ,d . yMAX M zel ,d M M zel ,d = Wzel . f yd
σ X max = = = zel ,d = f yd → (5.42)
Iz Iz Wzel
yMAX
siendo:
M zel ,d : "resistencia elástica de la sección a la flexión M z "
Iz
Wzel = :"módulo resistente elástico a la flexión M z "
ymax
Así pues para la comprobación a resistencia elástica de una sección trabajando a Flexión Pura:
Mz, se aplicará la fórmula:
M z* ≤ M zel ,d = Wzel . f yd (5.43)
Mz* (carga mayorada) = Mz.γ :
38

143. Sección 5.5: Introducción al dimensionamiento a resistencia de vigas metálicas solicitadas a flexión
Mz: momento flector que solicita a la sección, que se obtiene de los diagramas de esfuerzos
γ : coeficiente de seguridad para las cargas, (ver tabla 3.2)
Caso de una sección solicitada por un momento flector My:
De forma similar al caso anterior llegaríamos a los siguientes resultados:
La distribución de tensiones normales σx para este caso será ahora (ver fij.5.45):
σMAX(TRACCIÓN) = fyd
n z
G x
My = Myel,d
n
σMAX(COMPRESIÓN) = fyd
y
Fig.5.45
M yel ,d .zMAX M yel ,d M yel ,d
σ X max = = = = f yd → M yel ,d = Wyel . f yd (5.44)
Iy Iy Wyel
zMAX
siendo:
M yel , d :"resistencia elástica de la sección a la flexión M y "
Iy
Wyel = :"módulo resistente elástico a la flexión M y "
zmax
Así pues para la comprobación a resistencia elástica de una sección trabajando a Flexión Pura:
My, se aplicará la fórmula:
M * ≤ M yel ,d = Wyel . f yd
y (5.45)
My* (carga mayorada) = My.γ
My: momento flector que solicita a la sección, que se obtiene de los diagramas de esfuerzos
γ : coeficiente de seguridad para las cargas, (ver tabla 3.2)
Observación: Los módulos resistentes elásticos Wzel, Wyel, para el caso de series de perfiles
normalizados se pueden obtener en las tablas correspondientes a los mismos. En caso de
perfiles no normalizados se obtendrán a partir de sus expresiones respectivas..
Caso de los Momentos Flectores: Mz y My actuando simultáneamente:
En este caso la normativa propone la siguiente fórmula de cálculo:
M z* M*
+ y
≤1 (5.46)
M zel , d M yel ,d 39

144. Tema 5: Flexión: Tensiones
2.-Criterio plástico de dimensionamiento:
Según vimos en la sección 3.7: “La resistencia plástica de una sección se obtendrá cuando en
todos los puntos de la misma se alcance la tensión del límite elástico fy.”
Caso de una sección solicitada por un momento flector Mz:
Al momento flector Mz que produce la tensión del límite elástico fyd en todos puntos de la
sección, se le denomina: Mzpl,d y representa la resistencia plástica de una sección a la flexión
Mz. Calculemos su valor:
La distribución de tensiones normales σx para este caso será, (ver fig.5.46):
σ(COMPRESIÓN) = fyd
z
G n x Mz = Mzpl,d
n
σ (TRACCIÓN) = fyd
y
Fig.5.46
Para obtener la resistencia plástica Mzpl,d de la sección se procederá del siguiente modo:
∑M G = 0 → M zpl , d = ∫ σ .dA. y = (como σ = f yd = cte) = f yd .∫ y.dA =
A A
= f yd .2.∫ y.dA = Wzpl . f yd
A/ 2
M zpl ,d = Wzpl . f yd (5.47)
siendo:
M zpl ,d :"resistencia plástica de la sección a la flexión M z "
Wzpl = 2.∫ y.dA :"módulo resistente plástico a la flexión M z "
A/ 2
Así pues para la comprobación a resistencia plástica de una sección trabajando a Flexión
Pura: Mz, se aplicará la fórmula:
M z ≤ M zpl ,d = Wzpl . f yd
*
(5.48)
Mz* (carga mayorada) = Mz.γ :
Mz: momento flector que solicita a la sección, que se obtiene de los diagramas de esfuerzos
γ : coeficiente de seguridad para las cargas, (ver tabla 3.2)
40

145. Sección 5.5: Introducción al dimensionamiento a resistencia de vigas metálicas solicitadas a flexión
Caso de una sección solicitada por un momento flector My:
De forma similar al caso anterior llegaríamos a los siguientes resultados:
La distribución de tensiones normales σx para este caso será, (ver fig.5.47):
σMAX(TRACCIÓN) = fyd
n z
G x
My = Mypl,d
n
σMAX(COMPRESIÓN) = fyd
y Fig.5.47
Para obtener la resistencia plástica Mypl,d de la sección se procederá del siguiente modo:
∑M G = 0 → M ypl ,d = ∫ σ .dA.z = (como σ = f yd = cte) = f yd .∫ z.dA =
A A
= f yd .2.∫ z.dA = Wypl . f yd
A/ 2
M ypl ,d = Wypl . f yd (5.49)
siendo:
M ypl ,d :"resistencia plástica de la sección a la flexión M y "
Wypl = 2.∫ z.dA : "módulo resistente plástico a la flexión M y "
A/ 2
Así pues para la comprobación a resistencia plástica de una sección trabajando a Flexión
Pura: My, se aplicará la fórmula:
M * ≤ M ypl ,d = Wypl . f yd
y (5.50)
My* (carga mayorada) = My.γ :
My: momento flector que solicita a la sección, que se obtiene de los diagramas de esfuerzos
γ : coeficiente de seguridad para las cargas, (ver tabla 3.2)
Caso de los Momentos Flectores: Mz y My actuando simultáneamente:
En este caso la normativa propone la siguiente fórmula de cálculo:
M z* M*
+ ≤1
y
(5.51)
M zpl ,d M ypl ,d
41

146. Tema 5: Flexión: Tensiones
Observación: Los módulos resistentes plásticos Wzpl, Wypl, al igual que los elásticos, se
obtendrán: En el caso de series de perfiles normalizados, en las tablas correspondientes a los
mismos y en el caso de perfiles no normalizados, a partir de las expresiones respectivas
obtenidas para los mismos.
Ejemplo 1: Sección rectangular
b.h3 h.b3
I b.h 2 I h.b 2
Wzel = z = 12 = Wyel = y = 12 =
ymax h 6 zmax b 6
2 2
h G
z h b.h b.h2
Wzpl = 2.∫ y.dA = 2. yG ( A / 2) . A( A / 2) = 2. . =
A/ 2 4 2 4
b b.h h.b 2
Wypl = 2.∫ z.dA = 2.zG ( A / 2) . A( A / 2) = 2. . =
A/ 2 4 2 4
y
b
Ejemplo 2: Sección circular
R π .R 4
Iz 4 π .R 3
Wzel = = =
z ymax R 4
Wyel = (por simetría) = Wzel
4.R π .R 2 4 3
Wzpl = 2.∫ y.dA = 2. yG ( A / 2) . A( A / 2) = 2. . = .R
A/ 2 3.π 2 3
y Wypl = (por simetria) = Wzpl
Ejemplo 3: IPE-300
Wzel = (tablas) = 557,1 mm3
Wyel = (tablas) = 80,5 mm3
Wzpl = (tablas) = 628, 4 mm3
Wypl = (tablas) = 125, 2 mm3
42

147. Sección 5.5: Introducción al dimensionamiento a resistencia de vigas metálicas solicitadas a flexión
3.-Criterio de Von Mises de dimensionamiento:
Si aplicásemos el criterio de dimensionamiento de Von-Mises (sección 3.7), llegaríamos al
mismo resultado que con el criterio elástico de dimensionamiento.
En efecto, la fórmula de Von Mises es: σ co = σ *2 + 3.τ *2 ≤ f yd
Caso del Momento Flector: Mz:
* * *
M z . ymax Mz Mz
siendo : σ = *
= = τ* = 0 y sustituyendo
Iz I z / ymax Wzel
*
Mz
σ co = ≤ f yd → M z* ≤ Wzel . f yd
Wzel
Caso del Momento Flector: My:
M * .zmax M* M*
siendo : σ * = = = τ* = 0
y y y
y sustituyendo
Iy I y / zmax Wyel
*
My
σ co = ≤ f yd → M y ≤ Wyel . f yd
*
Wyel
Caso de los Momentos Flectores: Mz y My actuando simultáneamente:
*
*
M z . ymax M y .zmax Mz *
M* *
M z* M y
siendo : σ = + = + = + τ* = 0
* y
Iz Iy I z / ymax I y / zmax Wzel Wyel
y sustituyendo
* *
*
Mz My Mz *
My M z* M*
σ co = + ≤ f yd → + ≤1 → +
y
≤1
Wzel Wyel Wzel . f yd Wyel . f yd M zel , d M yel ,d
Observación: La Normativa indica las clases de secciones a las que aconseja aplicar el cálculo
elástico o el plástico.
43

148. Tema 5: Flexión: Tensiones
5.5.2.-RESISTENCIA DE LAS SECCIONES A CORTADURA
Para el cálculo debido a las Fuerzas Cortantes, la normativa propone un cálculo plástico de las
mismas suponiendo unas distribuciones de tensiones cortantes uniformes.
1.-Criterio plástico de dimensionamiento:
El estudio se hará indistintamente para las cortaduras: Vy o Vz y la denominaremos en
general: V
A la fuerza cortante V que producen la tensión cortante del límite elástico τyd en todos puntos
de la sección, se le denomina: Vpl,d y representa la resistencia plástica de una sección a la
cortadura V. Calculemos su valor:
Según vimos en la sección 3.7, en el criterio de dimensionamiento de Von Mises, la tensión
cortante en el límite elástico tenía el siguiente valor :
f yd
τ yd = (ver ecuación 3.27)
3
Si suponemos, como dijimos antes, una distribución uniforme de las tensiones cortantes a lo
largo de la sección, tendremos:
τ = τyd = fyd/√3 =
cte
Vpl,d
Fig.5.48
Para obtener la resistencia plástica de la sección a esfuerzos cortantes, se procederá del
siguiente modo:
∑F =0→ V pl ,d = ∫ τ .dA = (como τ = τ yd = cte) = τ yd .∫ dA = (y por la ecuación 3.27) =
Av Av
f yd
= . Av
3
44

149. Sección 5.5: Introducción al dimensionamiento a resistencia de vigas metálicas solicitadas a flexión
Quedará pues:
f yd
V pl ,d = Av . (5.52)
3
siendo:
V pl ,d : "resistencia plástica de la sección a la cortadura V"
Av :"área de la sección a considerar, según el tipo de la misma ":
• Secciones macizas de gran espesor: rectangulares, circulares,…….
Av = A (área de la sección)
• Perfiles abiertos de pequeño espesor: IPE, HEB, UPN,……….
Con cortadura Vy: Av = Área del alma del perfil
Con cortadura Vz: Av = Área de las alas del perfil
• Perfiles cerrados de pequeño espesor circulares:
Av = A.2/π
• Perfiles cerrados de pequeño espesor rectangulares:
Con cortadura Vy: Av = Área de las almas de los perfiles
Con cortadura Vz: Av = Área de las alas de los perfiles
Ejemplo:
tf
Vy → Av ≈ h.tw
h tw
d Vz → Av ≈ A-.d.tw
b
45

150. Tema 5: Flexión: Tensiones
Así pues para comprobar la resistencia plástica de una sección a cortadura:
f yd
V * ≤ Vpl , d = Av . (5.53)
3
V* (carga mayorada) = fuerza cortante que solicita a la sección, que se obtiene de los
diagramas de esfuerzos
γ : coeficiente de seguridad para las cargas, (ver tabla 3.2)
2.-Criterio de Von Mises de dimensionamiento:
Si aplicásemos el criterio de dimensionamiento de Von-Mises (sección 3.7), sólo para las
Fuerzas Cortantes, llegaríamos al mismo resultado que con el criterio plástico de
dimensionamiento visto anteriormente.
En efecto, la fórmula de Von Mises es: σ co = σ *2 + 3.τ *2 ≤ f yd
V*
siendo : σ = 0
*
τ = (sup oniendo distribución uniforme) =
*
Av
V* f yd
y sustituyendo : 3. ≤ f yd → V * ≤ Av .
Av 3
5.5.3.-RESISTENCIA DE LAS SECCIONES A FLEXIÓN SIMPLE: MOMENTOS
FLECTORES Y FUERZAS CORTANTES
Se estudiarán los dimensionamientos vistos para los Momentos Flectores y para las Fuerzas
Cortantes separadamente y si se cumple que:
1 1 f
V * ≤ .V pl ,d = . Av . yd → no habrá que hacer mas comprobaciones
2 2 3
Esto ocurrirá en la mayoría de los casos y en el caso de que no se cumpliese habría que hacer
una nueva comprobación combinando el Momento flector con la Fuerza Cortante (ver
Normativa DB-SE-A)
46

151. Sección 5.5: Introducción al dimensionamiento a resistencia de vigas metálicas solicitadas a flexión
5.5.4.-RESISTENCIA DE LAS BARRAS METÁLICAS A FLEXIÓN
Al considerar ahora la barra en su conjunto, se tendrán que hacer nuevas comprobaciones:
1.- Comprobación del Pandeo Lateral debido a la flexión: al tener la viga zonas comprimidas,
si éstas no presentan una rigidez suficiente, la viga, si no está suficientemente rigidizada
lateralmente, podrá flexar lateralmente al mismo tiempo que torsionarse. Esto puede ocurrir
en vigas metálicas.
⇒
Fig.5.49.a
Fig.5.49.b
2.-Comprobación de la rigidez del alma de una barra bajo cargas concentradas
3.-Abolladura del alma por cortante
Ëstas comprobaciones son objeto de estudio en otras asignaturas. (Ver la Normativa española
sobre Estructuras de acero en la edificación: DB-SE-A)
Para otros materiales existen las Normativas específicas: caso del Hormigón y madera
47

152. Tema 5: Flexión: Tensiones
OBSERVACIONES:
Para efectuar el dimensionamiento completo de una viga que trabaje a Flexión habrá que
realizar, además del dimensionamiento a resistencia que se acaba de ver, la comprobación a
rigidez: limitación de la flecha máxima. (Se verá en el capítulo siguiente)
ymax
Fig.5.50
48

153. Tema 6: Flexión: Deformaciones
Tema 6: FLEXIÓN: DEFORMACIONES
x
+
y
1

154. Tema 6: Flexión: Deformaciones
6.1.- INTRODUCCIÓN
Las deformaciones hay que limitarlas al igual que las tensiones, bien por razones de
seguridad, de mantenimiento o simplemente de estética.
Así, en numerosos casos, los elementos estructurales se dimensionarán aparte de a
Resistencia, limitando sus tensiones máximas, (tal y como hemos visto en el tema
anterior), a RIGIDEZ, haciendo que las deformaciones máximas no sobrepases unos
determinados valores admisibles.
En diferentes normativas se fijan los valores admisibles de las deformaciones para
diferentes elementos estructurales.
Con el estudio de las deformaciones de una viga a Flexión, calcularemos los GIROS (θz
, θy ) que sufren las secciones transversales alrededor del eje neutro y las FLECHAS o
DESPLAZAMIENTOS (y, z) de sus centros de gravedad.
Flexión en plano xy Flexión en plano xz
θz θy
z
z
y x x
y
y z
Fig.6.1
Los métodos que desarrollaremos para el cálculo de las deformaciones son los
siguientes:
• Método de la Ecuación Diferencial de la Línea Elástica
• Método de la Ecuación Universal de la Línea Elástica
• Método de los Teoremas de Mohr
• Método energético del Teorema de Castigliano
• Método energético de los Trabajos Virtuales
Observación: Los dos métodos energéticos los estudiaremos más adelante, en el tema
9º, dado que son métodos de cálculo más generales y tienen su aplicación en el estudio
de las deformaciones, no sólo a Flexión, sino también en los casos de Tracción,
Compresión, Torsión, etc.
2

155. Sección 6.2: Método de la Ecuación Diferencial de la Elástica
6.2.-MÉTODO DE LA ECUACIÓN DIFERENCIAL DE LA ELÁSTICA
Consideremos la viga de la figura sometida a Flexión Simple (Ry, Mz)
x
Línea elástica y = y(x)
y
x
Fig.6.2
Según vimos en la sección 5.3.3. se denomina línea elástica: “al eje x de la viga (el que
pasa por los centros de gravedad de todas las secciones transversales), una vez
deformado”.
Tratemos ahora de calcular su ecuación: y = y(x)
Vimos también en dicha sección, que para el caso de Flexión Pura (sólo momentos
flectores), el radio de curvatura de la línea elástica venía dado por la ecuación (5.20):
1 Mz
=
r E .I z
pues bien, para el caso de la Flexión Simple (momentos flectores y fuerzas cortantes),
podremos utilizar la misma fórmula del radio de curvatura, pues la influencia que
ejercen las fuerzas cortantes es pequeña y la podremos despreciar en la mayoría de los
casos.
Por otra parte sabemos por Matemáticas que el radio de curvatura de una curva se puede
obtener de la expresión:
d2y
1 dx 2
= (6.1)
r   dy  2  3/ 2
1 +   
  dx  
 
igualando las expresiones del radio de curvatura:
d2y
dx 2 M
3/ 2
= z (6.2)
  dy  2  E .I z
1+   
  dx  
 
expresión obtenida que representa la “ecuación diferencial de la línea elástica”
La integración de esta ecuación diferencial, no lineal, presenta grandes dificultades y
dado que en la mayoría de los casos las deformaciones que se van a presentar, son
pequeñas, podremos hacer las siguientes simplificaciones:
3

156. Tema 6: Flexión: Deformaciones
θz
x
θz
y = y(x)
y
tangente
Fig.6.3
dy
= tagϑz ≅ ϑz (para pequeñas deformaciones) → Giros de las secciones
dx
si las deformaciones son pequeñas: θz es pequeño → tag θz es pequeño → dy/dx es
2
 dy 
pequeño → 1 +   ≅ 1 y haciendo esta aproximación en la ecuación (6.2) quedará:
 dx 
2
d y Mz d  dy  M dϑ z M z
2
= (6.3) o bien:   = z → = (6.4)
dx E .I z dx  dx  E.I z dx E.I z
Observación: con el sistema de ejes coordenados adoptado en el tema 5.2 para las vigas
a flexión, resultará que:
d2y
si M z > 0 → <0
dx 2
d2y
si M z < 0 → >0
dx 2
En efecto, supongamos: Mz >0
x2
x1
x
θ2
y
tag1 θ1 tag2
Fig.6.4
si x2 > x1 → dx > 0 y además según se ve en la fig.6.4 : ϑ2 < ϑ1 → dϑ < 0
dϑ d2y
< 0 o lo que es lo mismo : 2 < 0
con lo cual se cumplirá :
dx dx
y lo mismo se comprobaría para el caso: Mz<0.
4

157. Sección 6.2: Método de la Ecuación Diferencial de la Elástica
En virtud de ello en las ecuaciones (6.3) y (6.4) deberemos introducir un signo (-)
quedando finalmente como Ecuación diferencial de la línea elástica :
d2y M dϑ z M
2
=− z (6.5) o bien: =− z (6.6)
dx E .I z dx E.I z
OBSERVACIONES:
1.- Integrando una vez la Ecuación diferencial de la línea elástica obtendremos los Giros
θz (ver ecuación 6.6). Si integramos dos veces dicha ecuación obtendremos las Flechas
y de los centros de gravedad de cada sección (ver ecuación 6.5) o lo que es lo mismo la
Ecuación de la línea elástica: y = y(x)
2.- La ecuación de la línea elástica: y = y(x), es una función continua (ver figura 6.5.a).
Si fuera discontinua (ver figura 6.5.b), es que se habría roto
Fig.6.5.a Fig.6.5.b
3.- La ecuación de los giros: θz = θz (x), es también una función continua. Sería
discontinua sólo si la elástica presentase un punto anguloso (ver fig.6.5.c)
θ1
θ2
tag 1 tag θ1
tag 2
punto anguloso
Fig.6.5.c
1
En un punto anguloso se ha de verificar: =∞ ,entonces la ecuación (5.20), antes
r
1 Mz
mencionada, quedará: = = ∞ y para que esto se cumpla → M z = ∞ . Pero
r E.I z
éste valor nunca se va a dar.
d2y
4.- La ecuación diferencial de la elástica será discontinua en los puntos en que
dx 2
Mz sea discontinuo.
5

158. Tema 6: Flexión: Deformaciones
5.- Si en una sección de una viga es Mz = 0, la elástica presentará un punto de inflexión
en dicho punto
d2y M d2y
2
=− z =0 → = 0 → puntos de inflexión de la elástica y = y ( x )
dx E .I z dx 2
6.- Si la viga hubiese estado sometida a flexión simple en el plano xz: Rz, My, las
ecuaciones diferenciales (6.5) y (6.6) de la elástica serían:
d 2z My (6.7) dϑ y My (6.8)
2
=− =−
dx E .I y dx E .I y
7.- Si la viga estuviese sometida a flexión en ambos planos: xy y xz habría que calcular
por separado los giros y flechas relativos a ambos planos con las ecuaciones: (6.5),
(6.6), (6.7), y (6.8) . A continuación se compondrían vectorialmente los giros: θz, θy y
las flechas: y, z
r r r
giro total: ϑ = ϑz + ϑ y ϑ = ϑ z2 + ϑ y2
r r r
flecha total: δ = y+z δ = y2 + z2
z
Elástica en plano xx debida a la flexión My
z
x
δ
y
y
Elástica en plano xy debida a la flexión Mz
Fig.6.6
6

159. Sección 6.3: Método de los Teoremas de Mohr
6.3.-MÉTODO DE LOS TEOREMAS DE MOHR
Primer Teorema de Mohr:
El primer teorema de Mohr nos permite calcular el ángulo θAB que forman entre sí dos
secciones A y B de una viga flexionada. Éste ángulo será el mismo que el que forman
las tangentes a la elástica en los puntos A y B
θAB
x
θB
A
B tag en B
y
x dx θAB θA
tag en A
A B x
Mz
Mz Fig.6.9
La ecuación diferencial de la elástica es, según ecuación 6.6:
dϑ z M M z .dx
=− z → dϑ z = −
dx E .I z E .I z
e integrando esta ecuación entre los puntos A y B :
B B B
M z .dx M z .dx
∫ dϑ z = − ∫
A A
E .I z
→ ϑz ( B ) − ϑz ( A) = − ∫
A
E .I z
o bien :
B
M z .dx
ϑ z ( AB ) = ϑ z ( A) − ϑ z ( B ) = ∫ (6.15)
A
E .I z
7

160. Tema 6: Flexión-Deformaciones
Caso particular:
En el caso de que el módulo de rigidez de la viga sea constante: E.Iz = cte, la ecuación
6.15. se podrá expresar también de la siguiente manera:
B
B
M .dx ∫M z .dx
S M AB (6.16)
ϑz ( AB ) = ϑz ( A) − ϑz ( B ) = ∫ z = ( E .I z = cte) = A
=
A
E .I z E .I z E .I z
ecuación que nos dice: “el ángulo θz (AB) que forman entre sí dos secciones de la viga
flexionada, es igual al área del diagrama de momentos flectores comprendida entre A y
B: ( S M AB ) , dividido por el módulo de rigidez de la viga: E.Iz”
Observaciones:
1º.- En las expresiones del primer teorema de Mohr se consideran positivos los ángulos
θz que vayan en sentido horario, siempre que la sección A esté situada a la izquierda de
la sección B.
2º.- En el caso de una viga en la que conozcamos una sección que no gire (por ejemplo
casos de empotramientos), podremos conocer mediante este teorema, de forma directa,
el giro de cualquier otra sección de la misma
θB
A
θA=0 B
Fig.6.10
ϑ AB = ϑ A − ϑB = (como ϑ A = 0) = −ϑB
8

161. Sección 6.3: Método de los Teoremas de Mohr
Segundo Teorema de Mohr:
El segundo teorema de Mohr nos da la distancia en vertical, δBA, que hay desde un
punto B de la elástica a la tangente en otro punto A de la elástica.
xB
x dx
xA
x
B
A C D B0
B2
tag en D
y B1 δ dθ θ
BA
tag en C
B´
x dx tag en A
xB - x
A B x
Mz
Mz
Fig.6.11
Para calcular δBA haremos lo siguiente: por dos puntos C y D de la elástica, muy
próximos, situados a una distancia: x y x+dx respectivamente, trazamos las tangentes,
las cuales interceptan al segmento BB´= δBA en el segmento diferencial B1B2, cuya
longitud será:
B1 B2 = B1 B0 − B2 B0 = ( xB − x ).tagϑ − ( xB − x ).tag (ϑ − dϑ )
y para el caso de pequeñas deformaciones
B1 B2 ≅ ( xB − x ).ϑ − ( xB − x ).(ϑ − dϑ ) = ( xB − x ).d ϑ
sumando las longitudes de los segmentos diferenciales B1B2 al mover los puntos C y D
desde A hasta B, tendremos la longitud total δBA que queremos calcular. Así:
B
δ BA = BB´ = ∫ ( x B − x ).dϑ
A
y si finalmente se sustituye el valor absoluto de dθ obtenido en el primer teorema de
Mohr:
M .( x − x ).dx
B
δ BA = ∫ z B (6.17)
A
E .I z
9

162. Tema 6: Flexión: Deformaciones
Caso particular:
En el caso de que el módulo de rigidez de la viga sea constante: E.Iz = cte, la ecuación
6.17. se podrá expresar también de la siguiente manera:
B
B
M .( x − x ).dx ∫M z .( xB − x ).dx M
QB AB (6.18)
δ BA =∫ z B = ( E .I z = cte) = A
=
A
E .I z E .I z E .I z
ecuación que nos dice: “la distancia en vertical: δBA que hay desde un punto B de la
elástica a la tangente en otro punto A de la misma, es igual al momento estático
respecto del primer punto B del área del diagrama de momentos flectores comprendida
M
entre ambos puntos: Q B AB , dividido por el módulo de rigidez a flexión de la viga: E.Iz”
Observaciones:
1º.- En las expresiones del segundo teorema de Mohr, cuando δBA>0, indicará que el
punto B está situado por encima de la tangente en A, independientemente, en este caso,
del orden en que estén situados los puntos A y B.
2º.- En el caso de una viga en la que conozcamos una sección que no gire (por ejemplo
casos de empotramientos), podremos conocer mediante este teorema, de forma directa,
la flecha en un punto cualquiera de la misma.
tag en A
x
A δBA = yB
B
y Fig.6.12
3º.- Si la flexión de la viga fuera debida a un momento flector My y por tanto la elástica
estuviera en el plano xz las expresiones de los teoremas de Mohr: (6.15), (6.16), (6.17)
y (6.18), serían las mismas, sin más que cambiar:
Mz → M y E.Iz → E.Iy
y los giros y flechas obtenidos serían:
θz → θ y y → z
4º.- Si la flexión de la viga fuese debida a Mz y My conjuntamente se procedería de
forma análoga a lo indicado para los otros dos métodos expuestos.
10

163. Tema 7: Flexión: Hiperestaticidad
Tema 7: FLEXIÓN: HIPERESTATICIDAD
1

164. Tema 7: Flexión: Hiperestaticidad
7.1.- INTRODUCCIÓN
Según vimos en la sección 4.4 una viga o una estructura se dice que es hiperestática
cuando:
número de ecuaciones de equilibrio < número de incógnitas de las reacciones
Éstos casos suelen presentarse cuando la viga o la estructura tiene apoyos (ligaduras) de
más
Se denomina “grado de hiperestaticidad” :a la diferencia entre el número de incógnitas
de las reacciones y el número de ecuaciones de equilibrio de la estática.
También vimos que para resolver la hiperestaticidad era necesario añadir “ecuaciones
de deformación”, tantas como sea el grado de hiperestaticidad, de tal forma que:
nº ecuaciones de equilibrio+ nº ecuaciones de deformación=nº incónitas
El método de resolución será el transformar la viga hiperestática en una viga isostática
equivalente, liberándola de sus ligaduras de más y sustituyendo sus acciones por fuerzas
o momentos de magnitudes tales que la viga isostática conserve las coacciones que las
ligaduras ejercían sobre la viga hiperestática.
En este tema estudiaremos las vigas hiperestáticas de un solo tramo y las de dos o mas
tramos (vigas continuas), trabajando a flexión.
7.2.-VIGAS DE UN SOLO TRAMO
Hagamos su estudio a través del siguiente ejemplo:
MA q nº ecuaciones equilibrio:2
∑F =0 R A + R B = q .L (1)
A B L
RA RB
∑M A =0 R B .L + M A = q .L.
2
(2)
L Fig.7.1
nº incógnitas de las reacciones: 3
RA, MA, RB
Es una viga hiperestática de primer grado. Tiene una ligadura de más, pues podríamos
suprimir en ella el apoyo B o bien sustituir el empotramiento en A por un apoyo
articulado fijo, según se muestra a continuación:
q q
A B
A B
L Fig.7.2
L
2

165. Sección 7.2: Vigas de un solo tramo
Si suprimimos el apoyo B, la viga isostática que resulta, para que fuera equivalente a la
dada, deberíamos incluir la fuerza RB e imponer la condición (ecuación de
deformación):
MA q
yB = 0 (3)
A B
RA RB
L
Fig.7.3
Resolviendo el sistema formado por las ecuaciones: (1), (2) de equilibrio y la ecuación
(3) de deformación obtendríamos las reacciones en los apoyos: RA, MA, RB
Si hubiésemos optado por suprimir el empotramiento en A por un apoyo articulado fijo,
la viga isostática que resulta, para que fuera equivalente a la dada, deberíamos incluir el
momento MA e imponer la condición (ecuación de deformación):
MA q
A B ϑA = 0 (3)
RA RB
L Fig.7.4
Resolviendo el sistema formado por las ecuaciones: (1), (2) de equilibrio y la ecuación
(3) de deformación obtendríamos las reacciones en los apoyos: RA, MA, RB
7.3.-VIGAS CONTINUAS
Las vigas continuas son vigas que tienen más de dos apoyos. Normalmente se utilizan
cuando los vanos a cubrir son grandes.
Fig.7.5
No obstante, para cubrir esos vanos grandes, se podría optar por colocar varias vigas de
un solo tramo a continuación una de otra:
Fig.7.6
3

166. Tema 7: Flexión: Hiperestaticidad
Ventajas de las vigas continuas frente a las varias vigas de un solo tramo
Las vigas continuas dan momentos flectores y flechas de menor magnitud que las de un
solo tramo. Ésto se puede apreciar en el ejemplo de las figuras 7.7.a y b., abajo
representadas, lo que lleva consigo vigas de menor sección transversal y por tanto, más
económicas
Mz Mz
y y
Fig.7.7.a Fig.7.7.b
Por el contrario, los inconvenientes que presentan las vigas continuas frente a las de un
solo tramo, es que aquellas son sensibles a los desplazamientos (asientos) que puedan
sufrir los apoyos, lo que proporcionaría nuevos momentos flectores y por consiguiente
más tensiones inducidas.
Procedimiento para el cálculo de las vigas continuas
Las vigas continuas son vigas hiperestáticas y por tanto podremos resolverlas según el
procedimiento general, visto en 7.1, a través de la viga isostática equivalente
Ejemplo:
H1
1 2 3
R1 R2 R3 m-1 R Rm m
Fig.7.8 m-1
Esta viga tendrá:
nº ecuaciones de equilibrio: 3 ( ∑ Fx = 0 ∑F y =0 ∑M z = 0)
nº incógnitas de las reacciones: m+1 (H1, R1, R2, R3, ……Rm-1, Rm)
Es una viga hiperestática de grado m-2.
4

167. Sección 7.3: Vigas continuas
Utilizando para su cálculo el procedimiento descrito en 7.1, la “viga isostática
equivalente”, sería:
H1 2 3 m-1
1 m
R1 R2 R3 Rm-1 Rm
Fig.7.9
y las m-2 ecuaciones de deformación que habrá que añadir a ésta viga isostática para
que sea equivalente a la dada serán:
y 2 = 0 ; y 3 = 0 ;...... y m −1 = 0
Ahora ya con el sistema formado por las 3 ecuaciones de equilibrio y las m-2
ecuaciones de deformación indicadas, podremos resolver las m+1 incógnitas de las
reacciones.
No obstante para el cálculo de las vigas continuas existe otro procedimiento específico
para ellas, que se denomina: “Ecuación de los tres momentos”
ECUACIÓN DE LOS TRES MOMENTOS
Este método toma como incógnitas hiperestáticas los momentos flectores: M2, M3, Mm-1
que actuan en las secciones transversales correspondientes a los m-2 apoyos
intermedios.
Método de cálculo: se sustituye la viga continua por m-1 vigas isostáticas equivalentes,
simplemente apoyadas, en cuyos extremos se sitúan las ligaduras internas con los
tramos contiguos de los que las hemos liberado, es decir, las resultantes y los momentos
resultantes de las cargas que quedan a un lado de dichos extremos.: F2, M2, F3, M3, Fm-1,
Mm-1
H1
1 2 3
R1 R2 R3 m-1 R
m-1 Rm m
F2 F2
M2 M2 M3 F3 F3 M3 Fm-1
Mm-1
H1 3 3
1 2 2 m-1 m
R1 R2 R2 R3 R3 Rm-1 Rm
Fig.7.10
los Momentos Flectores: M2, M3,….Mm-1, se obtienen planteando las siguientes
ecuaciones de deformación:
ϑ2 (1,2) = ϑ2 (2,3), ϑ3 (2,3) = ϑ3 (3,4),........., ϑm−1 (m − 2, m − 1) = ϑm (m − 1, m)
5

168. Tema 7: Flexión: Hiperestaticidad
Desarrollemos pues a continuación estas ecuaciones de deformación y para ello
tomemos dos vigas isostáticas equivalentes, correspondientes a dos tramos consecutivos
n y n+1 de la viga continua:
Fn-1 Mn-1 Mn Fn Fn Mn Mn+1
Fn+1
n-1 n n n+1
Rn-1 Rn Rn Rn+1
Ln Ln+1
Fig.7.11
la ecuación de deformación a plantear será: ϑn ( n − 1, n) = ϑn ( n, n + 1) (7.1)
y para el cálculo de estos giros aplicamos el Principio de Superposición:
θ1n θ1 n
n-1 n n n+1
Ln Ln+1
θ2n
Mn-1 θ2 n Mn+1
n-1 n n n+1
Ln Ln+1
Mn θ3 n θ3 n M n
n-1 n n n+1
Ln Ln+1
Fig.7.12.a Fig.7.12.b
la ecuación de deformación anterior será:
− ϑn ( n − 1, n ) + ϑn2 ( n − 1, n ) + ϑn3 ( n − 1, n ) = ϑn ( n, n + 1) − ϑn2 ( n, n + 1) − ϑn3 ( n, n + 1)
1 1
(7.2)
Calculemos a continuación cada uno de estos valores:
6

169. Sección 7.3: Vigas continuas
• Cálculo de: ϑn (n − 1, n) y ϑn (n, n + 1) :
1 1
n-1 n n+1
θ1n n θ1n
δn-1,n δn+1,n
tag en n tag en n
Ln Ln+1
Mz Mz
Fig.7.13.a Fig.7.13.b
Por el método de los Teoremas de Mohr:
M M
Qn −1−1,n
n
Qn −1−1,n
n
δ n −1,n = = ϑn ( n − 1, n).Ln
1
→ ϑn ( n − 1, n) =
1
(7.3)
E .I z Ln .E .I z
M M
Q n ,n+1 Q n ,n+1
δ n +1, n = n +1 = ϑn ( n, n + 1).Ln +1 →
1
ϑ ( n, n + 1) = n +1
1
n
(7.4)
E .I z Ln +1.E.I z
• Cálculo de: ϑn2 ( n − 1, n) y ϑn2 (n, n + 1) :
tag en n tag en n
δn-1,n Mn-1 θ 2
n θ 2
n Mn+1 δn+1,n
n-1 n n n+1
Ln Ln+1
Mn-1 Mn+1
Mz Mz
Fig.7.14.a Fig.7.14.b
Por el método de los Teoremas de Mohr:
1 1
M − M n −1.Ln . .Ln
Q n−1,n 2 3 M n −1.Ln
δ n −1,n = n −1 = = ϑn2 (n − 1, n).Ln → ϑn2 (n − 1, n) = (7.5)
E .I z E .I z 6.E.I z
1 1
M − M n +1.Ln +1. .Ln +1
Q n ,n+1 2 3 M n +1.Ln +1
δ n +1,n = n +1 = = ϑn2 (n, n + 1).Ln +1 → ϑn2 (n, n + 1) = (7.6)
E .I z E .I z 6.E.I z
7

170. Tema 7: Flexión: Hiperestaticidad
• Cálculo de: ϑn3 ( n − 1, n) y ϑn3 (n, n + 1) :
tag en n tag en n
δn-1,n θ3
n
Mn θ 3
n
δn+1,n
Mn
n-1 n n n+1
Ln Ln+1
Mn Mn
Mz Mz
Fig.7.15.a Fig.7.15.b
1 2
M n−1,n − M n .Ln . .Ln
Q M n .Ln
δ n −1,n = n −1
= 2 3 = ϑn3 (n − 1, n).Ln → ϑn3 (n − 1, n) = (7.7)
E .I z E.I z 3.E.I z
1 2
M − M n .Ln +1. .Ln +1
Q n ,n+1 2 3 M n .Ln +1
δ n +1,n = n +1 = = ϑn3 (n, n + 1).Ln +1 → ϑn3 (n, n + 1) = (7.8)
E .I z E .I z 3.E.I z
llevando finalmente todos los valores obtenidos a la ecuación (7.2):
M M
Q n −1−1, n
n
M .L M .L Q n +1, n +1
n
M .L M .L
− + n −1 n + n n = − n +1 n +1 − n n +1
L n .E .I z 6 .E .I z 3 .E .I z Ln +1 .E .I z 6 .E . I z 3 .E .I z
y multiplicando todos los términos por: (6.E.Iz) y ordenando, quedará finalmente la
denominada ECUACIÓN DE LOS TRES MOMENTOS:
⎡ QnM n −1, n QnM 1, n +1 ⎤
n
M n −1 .Ln + 2.M n .( Ln + Ln +1 ) + M n +1 .Ln +1 = 6.⎢ −1
+ +
⎥ (7.9)
⎢ Ln
⎣ Ln +1 ⎥ ⎦
Está ecuación se irá aplicando cada tres apoyos sucesivos de la viga continua
8

171. Sección 7.3: Vigas continuas
CASO DE ASIENTOS EN LOS APOYOS
Ln n Ln+1
hn-1 n-1 hn
n+1
hn+1
n-1
n
Fig.7.16 n+1
separando ambas vigas:
Ln n n Ln+1 n+1
hn-1 n-1 hn θ4n
hn hn+1
θ4n θ4n
n-1
n n θ4n
n+1
Fig.7.17.a Fig.7.17.b
hn − hn −1 hn +1 − hn
tagϑn4 ≅ ϑn4 = tagϑn4 = ϑn4 = (7.10)
Ln Ln +1
planteando de nuevo la ecuación (7.1): ϑn (n − 1, n) = ϑn (n, n + 1) y añadiendo este
nuevo término, quedará:
− ϑn + ϑn2 + ϑn3 + ϑn4 (tramo n − 1, n) = ϑn − ϑn2 − ϑn3 + ϑn4 (tramo n, n + 1)
1 1
(7.11)
y sustituyendo los valores obtenidos para cada uno de ellos:
h − hn −1 h − hn
M M
Q n −1−1, n
n
M .L M .L Q n +1, n +1
n
M .L M .L
− + n −1 n + n n + n = − n +1 n +1 − n n +1 + n +1
L n .E .I z 6 .E . I z 3 .E .I z Ln Ln +1 .E .I z 6 .E .I z 3 . E .I z Ln +1
y multiplicando por (6.E.Iz) y ordenando, la Ecuación de los tres momentos quedará
ahora, teniendo en cuenta el descenso de los apoyos:
⎡ Q M n−1,n Q M n ,n+1 ⎤ ⎡h − h h −h ⎤
M n−1Ln + 2M n ( Ln + Ln+1 ) + M n+1Ln+1 = 6⎢ n−1 + n+1 ⎥ + 6EI z ⎢ n n−1 + n+1 n ⎥ (7.12)
⎣ Ln Ln+1 ⎦ ⎣ Ln Ln+1 ⎦
9

172. Tema 8: Torsión
Tema 8: TORSIÓN
1 2 T
G G
x
2´
1

173. Tema 8: Torsión
8.1.-INTRODUCCIÓN
Una sección de un elemento estructural está solicitada a Torsión cuando el Momento
resultante de las fuerzas interiores tiene la componente Mx = T
z
T x
G
y
Fig..8.1.a
Criterios de signos para los Momentos Torsores
T>0 → si su sentido es el de la normal saliente de la sección
T
n x n T x
T<0 → si su sentido es contrario al de la normal saliente en la sección
T n x n T x
Fig..8.1.b
En este tema se estudiarán elementos estructurales en los que todas sus secciones estén
solicitadas a Torsión
Diagramas de Momentos Torsores
Al igual que ocurre con los diagramas correspondientes de la Tracción-Compresión y de
la Flexión, los diagramas de Momentos Torsores indicarán el Momento Torsor
correspondiente a cada sección del elemento estructural.
Se desarrollará uno de estos diagramas a través de un ejemplo:
2

174. Sección 8.1: Introducción
Tramo L1
M1 M2 M3
M1 Mext = M1 n Mint = M1
L1 L2
T = M1
T
M1
Tramo L2
+
Mext = M3 Mint= M3 M3
x n
-
M3
Fig..8.2 T = - M3
Tipos de Torsión que se podrán dar:
A.-Torsión uniforme: Se dice que una barra trabaja a TORSIÓN UNIFORME cuando
se cumplan las dos condiciones siguientes: el único esfuerzo presente es un Momento
Torsor, que es constante a lo largo de ella y además los extremos de la barra pueden
alabear libremente
M M
L
T
M
+
x
Fig..8.3
En la torsión uniforme, dado que el alabeo que se pueda producir es el mismo en todas
las secciones, se podrá afirmar que las tensiones normales serán cero (σx = 0) , y sólo
dará lugar a tensiones cortantes: τ
3

175. Tema 8: Torsión
B.-Torsión no uniforme: Se dirá que la torsión no es uniforme cuando no se cumplan
algunas de las dos condiciones anteriores, como sería el caso de los dos ejemplos
siguientes:
Ejemplo 1 Ejemplo 2
M M1 M2 M3
Fig..8.4 Fig..8.5
T T
M = cte M1
+ +
x x
-
La sección de la izquierda está
empotrada y no podrá alabear M3
libremente
El Momento Torsor no es
constante a lo largo de la barra
En la torsión no uniforme, el alabeo posible de las diferentes secciones no será el
mismo, por lo que se producirán tensiones normales: σx y tensiones cortantes: τ.
En la siguiente figura se muestra el efecto del alabeo de una barra IPE laminada
sometida a torsión no uniforme (caso del ejemplo 2). Se observa cómo debido al alabeo,
las alas de la viga se flexionan y por tanto aparecerán en ellas tensiones normales σx
Fig..8.6
4

176. Sección 8.1: Introducción
Observaciones:
1. Para medir la susceptibilidad al alabeo por torsión de una determinada sección
se utiliza el denominado “módulo de alabeo”: Ia y para medir la susceptibilidad
la torsión se utiliza el “módulo de torsión”: It . Ambos valores se pueden
calcular u obtener de Tablas
2. Las piezas sometidas a Torsión no uniforme en las que el módulo de alabeo (Ia)
sea nulo o de pequeño valor con respecto al módulo de torsión (It), se admite
aplicar el cálculo como si fuera Torsión uniforme.
Éstos casos se darán en los siguientes tipos de secciones:
secciones macizas de gran espesor
secciones cerradas de pequeño espesor
secciones abiertas de pequeño espesor formadas por rectángulos que se cortan en
un punto
5

177. Tema 8: Torsión
Secciones más adecuadas para trabajar a torsión
En las piezas sometidas a torsión cabe distinguir dos tipos: el de las piezas cuya
principal función es la transmisión de un par torsor, sólo o combinado con esfuerzos de
flexión o axiles, (es el caso de piezas usadas principalmente en las máquinas: ejes, etc.)
y el de piezas en las cuales la torsión es un efecto secundario indeseable (es el caso, no
muy frecuente, de algunas piezas de estructuras de edificación, como las vigas carril o
las correas en fachadas laterales).
Las piezas correspondientes al primer tipo indicado, se proyectan con secciones macizas
de gran espesor o cerradas de pequeño espesor:
• SECCIONES DE GRAN ESPESOR (MACIZAS)
Circulares Circulares huecas Rectangulares
• SECCIONES CERRADAS DE PEQUEÑO ESPESOR
Circulares Rectangulares
Las SECCIONES ABIERTAS DE PEQUEÑO ESPESOR no son apropiadas para este
tipo de solicitación y deben tratar de evitarse su utilización o bien emplear disposiciones
constructivas adecuadas para evitar que la torsión se presente en ellas. Por ello su
cálculo no es frecuente y es estudiado con más profundidad en asignaturas de
Estructuras Metálicas
6

178. Sección 8.2: Tensiones y deformaciones en piezas de sección maciza: circular y circular hueca
8.2.-TENSIONES Y DEFORMACIONES EN PIEZAS DE SECCIÓN MACIZA:
CIRCULAR Y CIRCULAR HUECA
A.- CÁLCULO DE TENSIONES
Considérese una pieza de sección circular y sea T el momento torsor en una de sus
secciones
z
T
x
y Fig..8.7
Las relaciones Tensiones – Solicitaciones vistas en 1.7 serían para este caso:
N = 0 = ∫ σ x .dA V y = 0 = ∫ τ xy .dA Vz = 0 = ∫ τ xz .dA
A A A (8.1)
T = ∫ (τ xz . y − τ xy . z ).dA M y = 0 = ∫ σ x .z.dA M z = 0 = ∫ σ x . y.dA
A A A
Pero al igual que ocurría en la Tracción-Compresión y en la Flexión, éstas ecuaciones,
por si solas, no permiten calcular el valor de las tensiones originadas por el Momento
Torsor T. y habrá que recurrir nuevamente a hipótesis simplificativas que han sido
comprobadas experimentalmente. Para este caso será:
Hipótesis de Coulomb: “ Las secciones transversales circulares de la pieza permanecen
planas durante la Torsión, girando como un todo rígido alrededor del eje x normal a la
sección”
7

179. Tema 8: Torsión
Como consecuencia de dicha hipótesis se deduce que los radios de las secciones
transversales giran, permaneciendo rectos, mientras que las generatrices de la superficie
lateral (línea 1-2), se transforma en hélices (curva 1-2´)
1 2 T
G G
x
2´
Fig..8.8
Se demostrará a continuación que en la Torsión de piezas de sección circular no se
producen tensiones normales, es decir que: σx = 0
• Se supone en primer lugar que existen tensiones normales σx . Si fuese así, éstas
deberían presentar una distribución no constante, pues si fuese constante, es
decir: σx = cte, en virtud de la primera de las relaciones de la ecuación (8.1), se
tendría:
∫σ
A
x .dA = ( si σ x = cte) = σ x .∫ dA = σ x . A ≠ 0 ⇒
A
No se cumpliría dicha relación
Osea que tendría que ser: σx ≠ cte
σx
• Si σx ≠ cte, por la ley de Hooke: εx =
≠ cte
E
con lo cual se tendría que las deformaciones lineales εx serían diferentes para los
distintos puntos de una sección y ésta por tanto se alabearía, contradiciendo la
Hipótesis de Coulomb
1 1
2 2
3 3
4 4
5 5
Conclusión: ⇒ σx = 0 (8.2)
O lo que es lo mismo: “La torsión en secciones circulares sólo produce tensiones
cortantes τ “
8

180. Sección 8.2: Tensiones y deformaciones en piezas de sección maciza: circular y circular hueca
Cálculo de las tensiones cortantes
Se considera una rebanada de la pieza de longitud dx
1 2
ϕ ϕ +dϕ
1´ G G x
2´
dx
Fig..8.9
Mientras que la sección izquierda gira, alrededor del eje x, un ángulo ϕ (ángulo de giro
a torsión), la sección de la derecha habrá girado, en el mismo sentido, un ángulo ϕ + dϕ.
lo que supone un giro relativo a torsión de ésta sección con respecto a la anterior de
valor dϕ.
Se toma sobre dicha rebanada un prisma como el indicado en la siguiente figura
a b
d c G x
dx
Fig..8.10
Como consecuencia del giro de torsión relativo, dϕ, entre las dos secciones laterales de
dicha rebanada, el prisma se deformará, de tal forma que la cara lateral derecha girará
un ángulo dϕ con respecto a la cara lateral izquierda, dando lugar a la siguiente figura,
(que se ampliará para poder observarse mejor dicha deformación). La cara abcd del
prisma se transformará en la ab1c1d, sufriendo una deformación angular γ
dϕ b τ
a
γ a
γ
b
b1 r b1 τ
d c G τ
x c
c1 d
τ c1
dx Fig..8.11
9

181. Tema 8: Torsión
La deformación angular γ se podrá obtener por:
bb1 r.dϕ
tag γ ≅ γ = = = r.ϑ (8.3)
ab dx
dϕ
denominando θ = "ángulo de torsión unitario" (8.4)
dx
La deformación angular γ es el resultado de la acción de las tensiones cortantes que
actúan sobre las caras laterales del prisma. El valor de éstas se podrá obtener a partir de
la Ley de Hooke:
τ
γ= → τ = γ .G = ( según 8.3) = r .ϑ .G (8.5)
G
Ecuación que indica que: “en una sección circular, las tensiones cortantes τ
producidas por el Momento Torsor T, son proporcionales a la distancia r al centro de
la misma y perpendiculares al vector de posición r ”. Así pues, la distribución de
tensiones cortantes en una sección circular será la que se indica en las siguientes figuras
τmax
G
a τ b r
r τmax
τ d τ G
τ c
R z
τmax
Fig..8.12 τmax
y
siendo: τ = G.r.ϑ y τ max = (cuando r = R ) = G.R.ϑ
“la tensión cortante máxima: τmax, se dará en los puntos del borde de la sección
circular”
La cuarta ecuación de la relación tensiones-solicitaciones, ecuaciones (8.1) era:
T = ∫ (τ xz . y − τ xy .z ) dA = (ver figura ) = ∫ τ .r.dA dr
A A
r τ
xy τ
y sustituyendo el valor de τ dado en (8.5) : O≡G z
T = ∫ G.r.ϑ .r.dA = G.ϑ .∫ r 2 .dA = G.ϑ .I o de donde : dA τxz
A A
T y
ϑ= “ángulo de torsión unitario” (8.6)
G .I o
Fig..8.13
siendo: G.Io = Módulo de rigidez a la torsión
(equivalente al módulo de rigidez a la flexión: E.Iz, visto en el tema 5º)
10

183. Sección 8.2: Tensiones y deformaciones en piezas de sección maciza: circular y circular hueca
Sustituyendo finalmente el valor obtenido en (8.6), para el cálculo del ángulo de torsión
unitario, en la ecuación (8.5):
T T .r
τ = G.r.ϑ = G.r. = (8.7)
G.I o Io
expresión final para el cálculo de la tensión cortante debida a la torsión, en el caso de
barras de sección circular.
T .R T T
Por lo visto antes: τ max = τ ( r = R ) = = = (8.8)
Io Io Wo
R
siendo : Wo = Io / R Módulo resistente a la torsión
(equivalente al módulo de resistente a la flexión: Wz = Iz / ymax, visto en el tema 5º)
Observación: Éstas fórmulas serán también aplicables a las barras macizas de sección
circular hueca
SECCIÓN CIRCULAR SECCIÓN CIRCULAR HUECA
τmax τmax
τmax τmax
G G
z Re z
τmax R τmax Ri
τmax τmax
y y
π .R 4 π .Re4 π .Ri4
Io = Io = −
2 2 2
τ max = τ (r = R ) τ max = τ (r = Re )
Fig..8.14.a Fig..8.14.b
11

185. Tema 8: Torsión
B.- CÁLCULO DE DEFORMACIONES
Las deformaciones que se provocan en una barra sometida a Torsión son los GIROS a
TORSION: ϕ, que se producen, al girar sus secciones transversales alrededor del eje
geométrico OX de la misma. El valor de éstos giros será:
El ángulo de torsión unitario según la ecuación (8.6) era:
dϕ T T
ϑ= = → dϕ = .dx
dx G.I o G.I o
e integrando esta ecuación entre dos secciones A y B de la barra:
B
T .dx
ϕ BA = ϕ B − ϕ A = ∫ (8.9) Giro relativo entre dos secciones A y B de la
A
G .I o barra
Caso particular: Si G.Io = cte, la ecuación (8.9) se podrá expresar:
B
∫ T .dx S T AB
ϕ BA = ϕ B − ϕ A = A
= (8.10)
G .I o G .I o
Expresión que nos dice: “ el giro relativo debido a la torsión entre dos secciones A y B,
es igual al área del diagrama de momentos torsores entre las dos secciones, dividido
por el módulo de rigidez a la torsión: G.Io”
Signos: ϕBA > 0 ⇒ B gira en sentido antihorario respecto a A (siempre que las
secciones consideradas A y B, la sección A esté a la izquierda de la B)
Observación final: Según lo indicado en 8.1, las fórmulas obtenidas para las tensiones
y las deformaciones serán válidas tanto para el caso de Torsión Uniforme como para el
de Torsión no Uniforme.
12

186. Sección 8.3: Tensiones y deformaciones en piezas de sección maciza no circulares
8.3.-TENSIONES Y DEFORMACIONES EN PIEZAS DE SECCIÓN MACIZA
NO CIRCULARES
La hipótesis de Coulomb: “……las secciones transversales permanecen planas durante
la torsión…”, válida para las secciones circulares, no es válida sin embargo para otro
tipo de secciones y por tanto en éstas otras, las secciones se alabearán.
T T T T
Fig..8.15
No obstante, en este tipo de secciones, el módulo de alabeo Ia es pequeño comparado
con el módulo de torsión It y entonces, según lo indicado en 8.1, se podrá estudiarlas
como si estuvieran sometidas a Torsión Uniforme, aunque se estuviera en el caso de
Torsión no Uniforme. Así pues, en este tipo de secciones sometidas a Torsión, sólo
aparecerán tensiones cortantes τ.
La determinación exacta de tensiones y deformaciones en una pieza de sección
cualquiera sometida a Torsión, se debe a Saint-Venant y forma parte de la Teoría de la
Elasticidad. Aquí se expondrán a continuación los resultados que se obtienen al aplicar
dicha teoría al caso se piezas de sección rectangular.
CASO DE SECCIÓN RECTANGULAR:
T
τ max = (8.11)
µ.b2 .h
se da en el punto medio del lado mayor
h τmax T
ϑ= (8.12)
β .G.h.b3
b Fig..8.16
Los valores de µ y de β dependen de la relación h/b:
h/b 1 1,5 1,75 2 2,5 3 4 6 8 10 ∞
µ 0,208 0,231 0,239 0,246 0,258 0,267 0,282 0,299 0,307 0,313 0,333
β 0,141 0,196 0,214 0,229 0,249 0,263 0,281 0,299 0,307 0,313 0,333
13

187. Tema 8: Torsión
8.4.-TENSIONES Y DEFORMACIONES EN PIEZAS DE SECCIONES
ABIERTAS DE PEQUEÑO ESPESOR
Ya se indicó en 8.1 que este tipo de secciones no son apropiadas para el trabajo a
Torsión y para los casos en que la torsión aparezca como efecto secundario, para evitar
la excesiva deformación o rotura a la que pueda dar lugar, deberán emplearse
disposiciones constructivas adecuadas para evitar el efecto de dichas consecuencias.
En este tipo de secciones sólo se va a estudiar el caso de la Torsión Uniforme.
Observación: Según se dijo anteriormente los casos de secciones abiertas de pequeño
espesor formadas por rectángulos que se cortan en un punto, como sería el cado de las
secciones en L o en simple T, aunque estén sometidas a Torsión no uniforme, su cálculo
se hará como si fuera Torsión uniforme
CASO DE TORSIÓN UNIFORME:
Para conocer la distribución de tensiones cortantes τ a lo largo de la sección se utiliza el
denominado “Método de analogía de la membrana”, propuesto por Prandtl y que dice:
“las tensiones cortantes no dependen de la curvatura del contorno de la sección, siendo
prácticamente las mismas que si dicho contorno fuese recto”. De acuerdo con ello:
equivalente
sm
sm
t
Fig..8.17 t
En virtud de ello, y en el caso de espesor constante t = cte, se podrán aplicar las mismas
fórmulas (8.11) y (8.12) vistas anteriormente para el caso de sección rectangular:
T T Mx Mx
τ max = = 2 ϑ= =
µ.b .h µ.t .sm
2
β .G.h.b 3
β .G.sm .t 3
Y en este caso, como h >> b, es decir, sm >> t, los coeficientes µ y β valdrán (ver tabla
en 8.3): µ = 0,333 = 1/3 β = 0,333 = 1/3
Así pues las formulas quedarán:
T T
τ max = (8.13)
ϑ= (8.14)
1 2 1
.t .sm .G.sm .t 3
3 3
14

188. Sección 8.4: Tensiones y deformaciones en piezas de sección abierta de pequeño espesor
La teoría de Prandtl también dice: “…las tensiones cortantes máximas se dan en los
bordes del contorno, llevando en ambos lados sentidos opuestos y se admite que su
variación es lineal a lo largo del espesor”
τmax τmax
τmax τmax
equivalente
sm
sm τmax τmax
τmax
τmax
t
Fig..8.18 t
Casos particulares:
1. En el caso de que el espesor t de la sección no sea constante: t ≠ cte , las
ecuaciones anteriores se generalizarán de la siguiente forma:
T
τ max = sm
1 2 (8.15)
3 ∫
t τmax(t) . t .dsm
0
T
sm ϑ= sm (8.16)
τmax(tmax) 1
.G. ∫ t 3 .dsm
3 0
tmax
Fig..8.19
2. En el caso de que el espesor t de la sección no sea constante: t ≠ cte , pero que
ésta estuviese formada por varios elementos de espesor constante, las
ecuaciones anteriores serían ahora:
s1
T
t1 = tmax τ max = (8.17)
1
τmax(tmax) .∑ ti2 .si
t2 3
s2 T
ϑ=
1 (8.18)
.G.∑ ti3 .si
3
τmax(t3)
t3
s3
Fig..8.20
T .t
La tensión cortante máxima para cualquier espesor t se obtendrá: τ max (t ) = (8.19)
It
15

189. Tema 8: Torsión
8.5.-TENSIONES Y DEFORMACIONES EN PIEZAS DE SECCIONES
CERRADAS DE PEQUEÑO ESPESOR
En este tipo de secciones, según lo que se indicó en la sección 8.1, el cálculo que
haremos será válido tanto para la torsión uniforme como para la torsión no uniforme,
por lo tanto las tensiones normales serán cero (σ = 0) y sólo habrá tensiones cortantes
(τ).
A.- CÁLCULO DE TENSIONES
Se considera una rebanada de una pieza de longitud dx sometida a un Momento Torsor
T.
a1 d
τ a2 c
T
t b e
dx Fig..8.21
Se sabe que las tensiones cortantes en los puntos del contorno: a1a2 , han de ser
tangentes al mismo y dado el pequeño espesor (t) de la sección, se admite que están
distribuidas uniformemente a lo largo del mismo.
Estableciendo el equilibrio de fuerzas del elemento bcde, que se representa a
continuación ampliado:
tc
c
d ∑F x =0
τc τc
τ b .tb .dx = τ c .tc .dx → τ b .tb = τ c .tc
⇒ τ .t (flujo cortante)=cte
τb τb
b
e “el flujo cortante: τ.t es constante a lo
tb dx largo de la sección transversal”
Fig..8.22
2
Como consecuencia de ello, las tensiones cortantes (τ), serán mayores donde el espesor
(t) sea menor, (al revés de lo que ocurre en las secciones abiertas de pequeño espesor).
tc
c
τc τ b .t b = τ c .t c
τb
b si t b > t c → τb <τc
e
tb dx
16 Fig..8.23
2

190. Sección 8.4: Tensiones y deformaciones en piezas de sección abierta de pequeño espesor
Tomando ahora momentos respecto del centro de gravedad G de la sección, de todas las
fuerzas que actúan en la misma:
dSm t
τ Sm dF = τ .dsm .t
r dAm
dF
z
sm = longitud línea media
T
Fig..8.24
y 2
T = ∫ dF .r = ∫ τ .dsm .t.r = (como τ .t = cte) = τ .t . ∫ r .dsm = τ .t. ∫ 2.dAm = τ .t .2. Am
sm sm sm
y despejando τ = T (8.20) τ:
2.t. Am
siendo: Am = “área encerrada por la línea media de la sección transversal”
Am
Fig..8.25
2
La tensión cortante máxima, por lo visto antes, se dará donde el espesor sea mínimo,
resultando siendo su valor:
T
τ max = (8.21)
2.tmin . Am
B.- CÁLCULO DE DEFORMACIONES
Para el cálculo de deformaciones se partirá de la ecuación obtenida en 3.3, aplicándola a
la rebanada de la pieza anteriormente descrita de longitud dx.:
dTe = dU
1
siendo: dTe = .T .d ϕ x “trabajo que realiza el momento torsor T”
2
1 1 2 1
dU = ∫ u.dV = ∫ .(τ xy + τ xz ).dV = ∫ .τ .dV = . τ 2 .dsm .t.dx = ( dx = cte) =
2.G s∫
2 2
V V
2.G V
2.G m
dx
= . ∫ τ 2 .t .dsm
2.G sm
“energía almacenada en la rebanada durante la deformación provocada por Mx”
17

191. Tema 8: Torsión
igualando ambas expresiones:
1 dx dϕ x 1 1 τ 2 .t 2
.T .dϕ x = . ∫ τ 2 .t.dsm T. = . ∫ τ 2 .t.dsm = . ∫ .dsm =
2 2.G sm dx G sm G sm t
τ 2 .t 2 dsm
(y como τ .t = cte) = .∫
G sm
t
τ .t
2 2
dsm T T2 dsm
T .ϑ = .∫ = (como τ = )= 2 ∫
. y despejando ϑ :
G sm
t 2.t. Am 4.G. Am sm t
T dsm
ϑ= 2 ∫
. (8.22)
4.G. Am sm t
Casos particulares:
T T s
1. Si t = cte ⇒ τ max = (8.23) θ= 2
. m (8.24)
2.t. Am 4.G. Am t
2. Si el espesor t de la sección no es constante: t ≠ cte , pero ésta estuviese
formada por varios elementos de espesor constante:
T T si
2 ∑
τ max = (8.25) θ= . (8.26)
2.tmin . Am 4.G. Am ti
OBSERVACIÓN FINAL: CUADRO RESUMEN
Con el objeto de unificar las fórmulas que se han obtenido para los diferentes tipos de
secciones, se podrá adoptar un formato general, único para todas ellas, que sería el
siguiente:
T
τ max = (8.27) siendo: It = momento de inercia torsor equivalente
Wt
T
ϑ= (8.28) siendo: Wt = módulo resistente a la torsión equivalente
G.I t
Los valores de It y de Wt para cada una de las secciones se obtendrán comparando las
fórmulas obtenidas para cada una de las secciones estudiadas con las dadas como
formato general. Así tendremos:
18

192. Sección 8.5: Tensiones y deformaciones en piezas de sección cerrada de pequeño espesor
a) sección circular : comparando las fórmulas específicas obtenidas para la sección
circular:
T T
ϑ= (8.6) τ max = (8.7)
G .I o Wo
con las generales de formato único:
T T
ϑ= (8.28) τ max = (8.27)
G.I t Wt
π .R 4 I o π .R 3
resultará: It = Io = Wt = Wo = = (8.29)
2 R 2
b) sección rectangular : comparando las fórmulas específicas obtenidas para la sección
rectangular:
T T
ϑ= (8.12) τ max = (8.11)
β .G.h.b3 µ.b2 .h
con las generales de formato único:
T
ϑ=
T
(8.28) τ max = (8.27)
G.I t Wt
resultará: I t = β .h.b 3 Wt = µ .b 2 .h (8.30)
c) secciónes abiertas de pequeño espesor: compararando las fórmulas específicas
obtenidas para las secciones abiertas de pequeño espesor t = cte:
T T
ϑ= (8.14) τ max = (8.13)
1 1 2
.G.sm .t 3 .t .sm
3 3
con las generales de formato único:
T T
ϑ= (8.28) τ max = (8.27)
G.I t Wt
1 1
resultará: I t = .s m .t 3 Wt = .s m .t 2 (8.31)
3 3
Observación: La Normativa española NBE-EA-95 corrige estos valores afectándolos de
un coeficiente α de la siguiente forma:
1 1
I t = α . .s m .t 3 Wt = α . .s m .t 2 (8.32)
3 3
19

193. Tema 8: Torsión
siendo el valor de α:
α SECCIÓN
1
1,1
1,3
Y para el caso estudiado de que el espesor t de la sección no sea constante: t ≠ cte , pero
que ésta estuviese formada por varios elementos de espesor constante, comparando de
nuevo las ecuaciones obtenidas para este caso específico con las fórmulas generales
únicas, y ya incluyendo el valor α corrector que incluye la normativa española NBE-
AE-95, sería:
1 1
I t = α . .∑ s i .t i3 Wt = α . .∑ s i .t i2 (8.33)
3 3
d) secciónes cerradas de pequeño espesor: compararando las fórmulas específicas
obtenidas para las secciones cerradas de pequeño espesor t = cte
T s T
θ= 2
. m (8.24) τ max = (8.23)
4.G. Am t 2.t. Am
con las generales de formato único:
T T
ϑ= (8.28) τ max = (8.27)
G.I t Wt
2
4. Am .t
resultará It = Wt = 2.t min . Am (8.34)
sm
Si el espesor t de la sección no es constante: t ≠ cte , pero ésta estuviese formada por
varios elementos de espesor constante:
2
4. Am
It = Wt = 2.t min . Am
s (8.35)
∑ ti
i
20

194. Sección 8.5: Tensiones y deformaciones en piezas de sección cerrada de pequeño espesor
Ejemplos
1.-SECCIÓN CIRCULAR DE PEQUEÑO ESPESOR
Am = π .rm
2
rm s m = 2.π .rm
t = cte
Wt = 2.t min . Am = 2.t.π .rm
2
Am
4. Am .t 4.(π .rm ) 2 .t
2 2
It = = = 2.π .rm .t
3
sm 2.π .rm
Fig..8.26
2
2.-SECCIÓN RECTANGULAR DE PEQUEÑO ESPESOR
t2
Am = bm .hm
t1 s m = 2.bm + 2.hm
Wt = 2.t min . Am = 2.t1 .bm .hm
hm Am
2 2 2
4. Am .t 4.bm .hm
It = =
si b h
∑ t 2. t m + 2 . t m
i 2 1
bm
Fig..8.27
2
21

195. Tema 8: Torsión
5.5-INTRODUCCIÓN AL DIMENSIONAMIENTO A RESISTENCIA DE VIGAS
METÁLICAS SOLICITADAS A TORSIÓN (Normativa DB-SE-A)
RESISTENCIA DE LAS SECCIONES A TORSIÓN
El esfuerzo torsor T de cualquier sección puede dividirse en dos componentes:
T = Tt + Tw (8.36)
siendo:
Tt : componente correspondiente a la torsión uniforme
Tw : componente correspondiente a la torsión de alabeo
• En las piezas de secciones macizas de gran espesor o en las cerradas de pequeño
espesor puede despreciarse la componente Tw, con lo cual: T = Tt
• En las piezas de secciones abiertas de pequeño espesor puede despreciarse la
componente de torsión uniforme Tt, con lo cual: T = Tw
La comprobación a resistencia puede realizarse de acuerdo a la expresión de Von
Misses
Observación: En esta asignatura tal y como dijimos anteriormente, tan sólo
dimensionaremos, en el caso de la Torsión, con secciones macizas de gran espesor o
cerradas de pequeño espesor
Criterio de dimensionamiento de Von Misses:
σ co = σ *2 + 3.τ *2 ≤ f yd
Se calcularán las tensiones cortantes debidas a Tt y las tensiones normales y cortantes
debidas a Tw. Con los valores obtenidos de todas estas tensiones se introducirán en la
fórmula de Von Misses.
22

196. Tema 9: Solicitaciones Combinadas
Tema 9: SOLICITACIONES COMBINADAS
z
Vz
T N
x
Mz
My
L
Vy
y
1

197. Tema 9: Solicitaciones Combinadas
9.1.-INTRODUCCIÓN
En los temas precedentes se ha estudiado el cálculo de las tensiones y deformaciones
producidas por las siguientes solicitaciones actuando de forma aislada:
TRACCIÓN-COMPRESIÓN:
• Tensiones normales: σx (N)
• Deformaciones: alargamientos o acortamientos: ∆L
FLEXIÓN SIMPLE:
• Tensiones normales: σx (Mz, My)
• Tensiones cortantes: τ (Vy, Vz)
• Deformaciones: Giros: θz, θy
• Deformaciones: Flechas: y, z
TORSIÓN:
• Tensiones cortantes: τ (T)
• Deformaciones: Giros: θx
En este tema se estudiarán las tensiones y deformaciones que se producirán cuando
actúen a la vez varias de éstas solicitaciones: Tracción + Flexión, Flexión + Torsión,
etc..
Cálculo de las Tensiones:
Se obtendrán aplicando el Principio de Superposición:
σ x = σ x ( N ) + σ x (M z , M y )
r r r
τ = τ (V y , Vz ) + τ (T )
(la suma de las tensiones cortantes:τ, será vectorial, pues pueden llevar distintas
direcciones)
Cálculo de las Deformaciones:
Se pueden obtener a partir del Principio de Superposición, igual que con las tensiones,
o a través de los teoremas energéticos que se verán a continuación:
• Teorema de CASTIGLIANO
• Teorema de los TRABAJOS VIRTUALES
2

198. Sección 9.2.1: Energía de deformación
9.2.-TEOREMAS ENERGÉTICOS
9.2.1.- ENERGÍA DE DEFORMACIÓN
La energía de deformación de un elemento estructural se podrá obtener a partir de las
expresiones dadas en 3.4:
• Energía de deformación por unidad de volumen:
u=
1
2 .E
[ 2 2
]
. σ x + σ y + σ z2 − 2.ν .(σ x .σ y + σ y .σ z + σ z .σ x ) +
1
2.G
.(τ xy + τ yz + τ zx ) (9.1)
2 2 2
• Energía de deformación:
U = ∫ u.dV (9.2)
V
Se calculará a continuación la Energía de deformación: U, para el caso de elementos
estructurales sometidos a una sola solicitación:
A. TRACCIÓN-COMPRESIÓN: N
Componentes del estado de tensiones:
z
N
N σx = σy = 0 σz = 0
N A
x τ xy = 0 τ yz = 0 τ zx = 0
L y y llevando estos valores a
las expresiones (9.1) y (9.2):
Fig.9.1
2
2
1 ⎡N ⎤ 1 N 2 .dx
L
1 1 ⎛N⎞ U = ∫ u.dV = ∫ . ⎢ ⎥ . A.dx = .∫ (9.3)
u= .σ x =
2
.⎜ ⎟ 2.E ⎣ A ⎦ 2 0 E. A
2.E 2.E ⎝ A ⎠ V L
3

199. Tema 9: Solicitaciones Combinadas
B. FLEXIÓN SIMPLE:
B1.-Momento Flector: Mz (caso particular: Ejes z, y →Ejes principales de
inercia: Izy = 0)
Componentes del estado de tensiones:
z
M z .y
σx = σy = 0 σz = 0
Iz
Mz x τ xy = 0 τ yz = 0 τ zx = 0
L y y llevando estos valores a
las expresiones (9.1) y (9.2):
Fig.9.2
2
1 1 ⎛ M z .y ⎞
u= .σ x =
2
.⎜ ⎟
2.E 2.E ⎜ I z ⎟
⎝ ⎠
2
1 ⎡ M z .y ⎤ 1 M 2 .dx 1 M 2 .dx
L
U = ∫ u.dV = ∫ .⎢ ⎥ ..dV = .∫ z 2 .∫ y 2 .dA = .∫ z (9.4)
V V
2 .E ⎣ I z ⎦ 2 L E .I z A 2 0 E .I z
B2.-Momento Flector: My (caso particular: Ejes z, y → Ejes principales de
inercia: Izy = 0)
Componentes del estado de tensiones:
z
M y .z
σx = σy = 0 σz = 0
Iy
x
τ xy = 0 τ yz = 0 τ zx = 0
My
y por un procedimiento análogo al anterior,
L y llevando estos valores a las expresiones
Fig.9.3 (9.1) y (9.2) se llegaría a la siguiente
expresión::
2
1 M y .dx
L
U = .∫ (9.5)
2 0 E .I y
4

200. Sección 9.2.1: Energía de deformación
B3.-Fuerza Cortante: Vy (caso particular: Ejes z, y → Ejes principales de
inercia: Izy = 0)
• Caso de secciones macizas
Componentes del estado de tensiones:
z
σx = 0 σy = 0 σz = 0
Vy .Qz ( y ) Vy .Qz ( z )
x τ xy = τ yz = 0 τ zx =
t ( y ).I z t ( z ).I z
Vy y llevando estos valores a
L y las expresiones (9.1) y (9.2):
Fig.9.4
1 ⎛ ⎛ Vy .Qz ( y ) ⎞ ⎛ Vy .Qz ( z ) ⎞ ⎞
2 2
1
u= .(τ xy + τ zx ) =
2 2
.⎜ ⎜ ⎟ +⎜ ⎟ ⎟
2.G 2.G ⎜ ⎝ t ( y ).I z ⎠ ⎝ t ( z ).I z ⎠ ⎟
⎝ ⎠
1 Vy2 .Qz2 ( y ) Vy2 .Qz2 ( z )
U= .∫ u.dV = ∫ .dV + ∫ .dV =
2.G V V
2.G.t 2 ( y ).I z2 V
2.G.t 2 ( z ).I z2
Vy2 .dx Qz2 ( y ) V 2 .dx Q 2 ( z )
=∫ 2 ∫
. .dA + ∫ y 2 .∫ 2z .dA = multiplicando y dividiendo por A =
L
2.G.I z A t 2 ( y ) L
2.G.I z A t ( z )
Vy2 .dx A Qz2 ( y ) Vy2 .dx A Qz2 ( z )
=∫
2.G.I z2 A ∫ t 2 ( y )
.dA + ∫
2.G.I z2 A ∫ t 2 ( z )
. . . . .dA =
L A L A
1 Vy .dx ⎡ A Qz2 ( y ) A Qz2 ( z ) ⎤ 1 Vy .dx ´
L 2 L 2
= .∫ . ⎢ 2 .∫ 2 .dA + 2 .∫ 2 .dA⎥ = .∫ .( β y + β y )
´´
2 0 G. A ⎣ I z A t ( y ) I z A t ( z) ⎦ 2 0 G. A
1
L
Vy2 .dx
U = .β y .∫ (9.6)
2 0
G. A
A Qz2 ( y ).dA A Qz2 ( z ).dA
I z2 ∫ t 2 ( y ) I z2 ∫ t 2 ( z )
siendo: βy = βy + βy
´ ´´
βy =
´
. βy =
´´
.
A A
Observaciones:
6 6
en sec ciones rec tan gulares : β y =
´
βy = 0 → βy =
´´
5 5
10 10
en sec ciones circulares : βy =
´
βy = 0 →
´´
βy =
9 9
5

201. Tema 9: Solicitaciones Combinadas
• Caso de secciones abiertas de pequeño espesor
Componentes del estado de tensiones:
σx = 0 σy = 0 σz = 0
τ xy ≠ 0 τ yz = 0 τ zx ≠ 0
1 1 2 Vy .Qz ( s )
u= .(τ xy + τ zx ) =
2 2
.τ xs siendo τ xs =
2.G 2.G t ( s ).I z
1
L
Vy2 .dx
y por un procedimiento análogo al anterior: U = .β y .∫ (9.7)
2 0
G. A
A Qz2 ( s ).dA
I z2 ∫ t 2 ( s )
siendo: βy = .
A
A
Observaciones: en sec ciones I : β y =
Aalma
B4.-Fuerza Cortante: Vz (caso particular: Ejes z, y → Ejes principales de
inercia: Izy = 0)
• Caso de secciones macizas:
z
σx = 0 σy = 0 σz = 0
Vz Vz .Qy ( y ) Vz .Qy ( z )
τ xy = τ yz = 0 τ zx =
x t ( y ).I y t ( z ).I y
y por un procedimiento similar al caso de Vy:
Fig.9.5 L y
V 2 .dx
L
1
U = .β z .∫ z (9.8)
2 0
G. A
2 2
A Q y ( y ).dA A Q y ( z ).dA
siendo: βz = β + β
´
z
´´
z β = 2 .∫ 2
´
z β = 2 .∫ 2
´´
y
I y A t ( y) I z A t ( z)
Observaciones:
6 6
en sec ciones rec tan gulares : β z´ = 0 β z´´ = → βz =
5 5
10 10
en sec ciones circulares : β z´ = 0 β z´´ = → βz =
9 9
6

202. Sección 9.2.1: Energía de deformación
• Caso de secciones abiertas de pequeño espesor
Componentes del estado de tensiones:
σx = 0 σy = 0 σz = 0
τ xy ≠ 0 τ yz = 0 τ zx ≠ 0
1 1 2 Vz .Qy ( s )
u= .(τ xy + τ zx ) =
2 2
.τ xs siendo τ xs =
2.G 2.G t ( s ).I y
V 2 .dx
L
1
y por un procedimiento análogo al anterior: U = .β z .∫ z (9.9)
2 0
G. A
2
A Q y ( s ).dA
siendo: β z = 2 .∫ 2
I y A t (s)
C. TORSIÓN: T
• Caso de secciones macizas circulares
z Componentes del estado de tensiones:
T T
x σx = 0 σy = 0 σz = 0
τ xy ≠ 0 τ yz = 0 τ zx ≠ 0
L y Fig.9.6
2
1 1 2 1 ⎛ T .r ⎞
u= .(τ xy + τ zx ) =
2 2
.τ = .⎜ ⎟
2.G 2.G 2.G ⎝ I o ⎠
1 T 2 .dx
L
T 2 .r 2 T 2 .dx
U = .∫ (9.10) U = ∫ u.dV = ∫ 2
.dV = ∫ 2 ∫
. r 2 .dA →
2 0 G.I o V V
2.G.I o L
2.G.I o A
• Caso de secciones macizas no circulares o secciones de pequeño espesor
haciendo la sustitución : I o → I t " momento de inercia torsor equivalente"
1 T 2 .dx
L
U = .∫ (9.11)
2 0 G.I t
7

203. Tema 9: Solicitaciones Combinadas
D. CASO GENERAL: TRACCIÓN-COMPRESIÓN (N) + FLEXIÓN (Mz,
My, Vy, Vz) + TORSIÓN (T):
z
Vz
T N
x
Mz
My
L
Vy
Fig.9.7 y
Aplicando el Principio de Superposición, la energía de deformación total será la suma
de las energías de deformación obtenidas para cada una de las solicitaciones actuando
por separado, así será:
U = U ( N ) + U (V y ) + U (Vz ) + U (T ) + U ( M y ) + U ( M z )
y sustituyendo los valores obtenidos para cada uno de dichos términos:
1 N 2 .dx 1
L L
Vy2 .dx 1 L L L 2
Vz2 .dx 1 T 2 .dx 1 M y .dx 1 M z2 .dx
L
U= ∫ + .β y .∫ + .β z .∫ + ∫ + ∫ + ∫
2 0 E. A 2 0
G. A 2 0
G. A 2 0 G.I t 2 0 E.I y 2 0 E .I z
(9.12)
Observaciones:
Todos los términos de la expresión (9.12) no tienen el mismo orden de magnitud. Así
por ejemplo generalmente:
U (V y ), U (Vz ) <<< U (T ), U ( M y ), U ( M z )
con lo cual, en la mayoría de los casos, se suelen despreciar los términos debidos a las
fuerzas cortantes: U (V ), U (V )
y z
Igualmente, en la mayoría de los casos, se cumple que: U ( N ) << U ( M y ), U ( M z )
salvo en los casos de Tracción-Compresión con pequeña excentricidad
8

204. Sección 9.2.2: Teorema de Castigliano
9.2.2.- TEOREMA DE CASTIGLIANO
Sea un cuerpo elástico, apoyado de tal forma que le sea imposible moverse y sobre él se
aplican gradualmente las fuerzas: F1, F2, …., Fi, …., Fn.
Se supone que se cumplen las condiciones vistas en 3.3, por las que se podrá considerar
que el trabajo que realizan las fuerzas externas se transforma todo en energía de
deformación (campos conservativos)
Los desplazamientos que sufren los puntos de aplicación de dichas fuerzas: ∆i ( i→i2 ),
se descomponen en dos componentes, los desplazamientos δi (i→i1) que van en la
misma dirección que los vectores fuerza Fi, y los desplazamientos (i1→i2) en
direcciones perpendiculares a las anteriores.
Esta descomposición se hace así para que en el cálculo del trabajo que realizan las
fuerzas exteriores tan sólo haya que tener en cuenta las componentes δi, que van en la
misma dirección que las fuerzas aplicadas, pues las otras componentes, al ser
perpendiculares a las direcciones de las fuerzas aplicadas, no realizan trabajo.
F1 F2
δ1 δ2
Fi i δi i1
∆i i2
δn
Fn
Fig.9.8.a
La energía de deformación del cuerpo será función de las fuerzas aplicadas sobre él:
U = U ( F1 , F2 , .......Fi ,.......Fn )
Si se diera un incremento infinitesimal a una cualquiera de las fuerzas aplicadas, por
ejemplo la Fi, la energía de deformación sería:
F1 F2
∂U
U+ .dFi (9.13)
dFi Fi ∂Fi
Fn
Fig.9.8.b
9

205. Tema 9: Solicitaciones Combinadas
Si se considerase ahora un segundo estado de cargas, en el que se invierta el orden de
aplicación de las fuerzas externas, así, se aplica en primer lugar dFi y a continuación las
restantes fuerzas: F1, F2, …., Fi, …., Fn. La energía de deformación sería ahora:
F1 F2
1
.dFi .d δ i + U + dFi .δ i (9.14)
dFi 2
Fi
Fn
Fig.9.8.c
En efecto:
1
• al aplicar primero dFi, se realizará un trabajo de valor: .dFi .dδ i
2
• al aplicar a continuación el resto de las fuerzas: F1, F2, …., Fi, …., Fn, se
realizará un trabajo: U+dFi.δi
en donde el término: dFi.δi es el trabajo indirecto que realiza dFi, que ya estaba
aplicado, al aplicar ahora el resto de las fuerzas y desplazarse su punto de
aplicación δi.
Y como según se sabe, en el caso de campos conservativos: “el trabajo que realizan las
fuerzas externas es igual a la energía de deformación y su valor depende solamente de
los valores iniciales y finales de dichas fuerzas y no de su orden de aplicación”. Como
consecuencia de ello serán iguales los dos valores obtenidos de la energía de
deformación para los dos estados de cargas considerados, ecuaciones: (9.13) y (9.14).
Así pues se verificará:
∂U 1
U+ .dFi = .dFi .dδ i + U + dFi .δ i
∂Fi 2
y despreciando infinitésimos de 2º orden frente a los de 1º:
∂U ∂U
.dFi = dFi .δ i → δi = (9.15)
∂Fi ∂Fi
Teorema de Castigliano: “ el desplazamiento del punto de aplicación de una fuerza
exterior que actúa sobre un cuerpo, medido en dirección de la misma, es igual a la
derivada parcial de la energía de deformación respecto de dicha fuerza”
10

206. Sección 9.2.2: Teorema de Castigliano
Observaciones:
1. En el caso de que fuera un momento, en lugar de una fuerza, la carga que
actuase sobre el cuerpo, el giro producido se podría obtener de igual forma a
través del Teorema de Castigliano. Siguiendo un proceso análogo al anterior, la
relación sería en este caso:
∂U
ϑi = (9.16)
∂M i
2. La energía de deformación U, es la dada en (9.12)
1 N 2 .dx 1
L L
V 2 .dx 1 L L L 2
V 2 .dx 1 T 2 .dx 1 M y .dx 1 M z2 .dx
L
2 ∫ E. A 2
U= + .β y .∫ y + .β z .∫ z + ∫ + ∫ + ∫
0 0
G. A 2 0 G. A 2 0 G.I t 2 0 E.I y 2 0 E .I z
3. El Teorema de Castigliano determina los desplazamientos de los puntos de
aplicación de las fuerzas exteriores, en dirección de las mismas, así como los
giros de las secciones de aplicación de los momentos exteriores.
Fi
Fi
δi δi
θi
Mi
Fig.9.9.a
4. Si se quisiera calcular el desplazamiento δi de un punto donde no actuase
ninguna fuerza exterior, el Teorema de Castigliano se aplicaría de la siguiente
forma: se supondría que hubiese una fuerza Fi actuando en dicho punto, a
continuación se aplicaría el Teorema de Castigliano y finalmente se haría que
dicha fuerza fuese nula (Fi = 0)
F1 F2 Fi F2
F1
⇒
δi δi
Fig.9.9.b
⎛ ∂U ⎞
⎜ ∂F ⎟
δi = ⎜ ⎟ para Fi = 0
⎝ i⎠
11

207. Tema 9: Solicitaciones Combinadas
9.2.3.- TEOREMA DE LOS TRABAJOS VIRTUALES
Este Teorema dice: “ la condición necesaria y suficiente para que un cuerpo o sistema
material esté en equilibrio es que la suma de los trabajos de todas las fuerzas que
actúan sobre él, tanto exteriores como interiores, para cualquier conjunto de
desplazamientos que sean compatibles con los enlaces del cuerpo, sea nulo”
Τ´e + Τ´i = 0 (9.17)
siendo:
Τe´ → trabajo virtual de las fuerzas exteriores
Τi´ → trabajo virtual de las fuerzas int eriores
Cálculo de Τe´ : Τe´ = ∑ Fi .δ i´ + ∑ Ri .∆´i (9.18)
siendo: Fi → cargas exteriores aplicadas
Ri → reacciones externas en los apoyos
δ´i → desplazamientos virtuales en las direcciones Fi
∆´i → desplazamientos virtuales de los apoyos en las direcciones Ri
Cálculo de Τi´ :
Teniendo en cuenta que las fuerzas internas de una rebanada de un cuerpo, de longitud
dx, son iguales y opuestas a las fuerzas externas que actúan sobre ella, el trabajo virtual
que realizarán las fuerzas internas, durante la deformación virtual, será igual y de signo
opuesto al que realizan las fuerzas externas.
Se calculará a continuación el trabajo virtual de las fuerzas internas para dos tipos de
solicitaciones concretas:
TRACCIÓN-COMPRESIÓN (N)
N ( fuerza int erna ) = − Fe
Fe N N Fe Τ´i = − N .(ε ´x .dx )
desplazamiento virtual
dx Observación: el signo menos es
ε´x.dx debido a que las fuerzas interiores
Fig.9.10.a siempre se oponen a los
desplazamientos, por lo tanto irán
en sentidos contrarios y el trabajo será negativo.
12

208. Sección 9.2.3: Teorema de los Trabajos Virtuales
FLEXIÓN (Mz)
giro virtual
dθ´z
M z = ( momento int erno ) = − M e
Me Me
Τi´ = − M zi .( dϑ z´ )
Mz Mz
dx Fig.9.10.b
Repitiendo estos resultados para los restantes tipos de solicitaciones: Vy, Vz, T, My, se
tendrá como fórmula para el caso general que actuasen todos ellos:
L L L L L L
Τ´i = − ∫ N .(ε ´x .dx ) − ∫ V y .(γ ´xy .dx ) − ∫ Vz .(γ ´xz .dx ) − ∫ T .( dϕ ´x ) − ∫ M y .( dϑ y ) − ∫ M z .( dϑz´ )
´
0 0 0 0 0 0
Las expresiones de las deformaciones virtuales: ε´x, γ´xy, γ´xz, dϕ´x, dθ´y, dθ´z en
función de las correspondientes solicitaciones son:
N´ V y´ Vz´
ε ´x = γ ´xy = β y . γ ´xz = β z .
E. A G. A G. A
T .dx´
M ´y .dx ´
M z .dx
dϕ ´x = dϑ y =
´
dϑz´ =
G .I t E .I y E .I z
y sustituyéndolas en la expresión
del T´i se tendrá:
N .N ´
L L
V y .V y´ L
Vz .Vz´
L
T .T ´
L
M y .M ´y
Τ = −∫
´
i .dx − β y .∫ .dx − β z .∫ .dx − ∫ .dx − ∫ .dx −
0
E. A 0
G. A 0
G. A 0
G .I t 0
E .I y
L ´
M z .M z
−∫ .dx (9.19)
0
E .I z
Sustituyendo finalmente los valores obtenidos de T´e y T´i en la ecuación (9.17),
quedará finalmente:
N .N ´
L
V y .V y´
L L
Vz .Vz´
L
T .T ´
∑ Fi .δ + ∑ Ri .∆ = ∫ E. A .dx + β y .∫ G. A .dx + β z .∫ G. A .dx + ∫ G.I .dx +
i
´ ´
i
(9.20)
0 0 0 0 t
L
M y .M ´y L
M z .M z´
+∫ .dx + ∫ .dx
0
E .I y 0
E .I z
13

209. Tema 9: Solicitaciones Combinadas
Observaciones:
1. N, Vy, Vz, T, My, Mz → solicitaciones reales
N´, V´y, V´z, T´, M´y, M´z → solicitaciones virtuales (las correspondientes a
los desplazamientos virtuales)
2. El Teorema de los Trabajos Virtuales es más general que el Teorema de
Castigliano y puede aplicarse también al caso de que hubiese asientos en los
apoyos
3. Para aplicar el Teorema de los Trabajos Virtuales es conveniente hacerlo a
través del llamado “Método de la Carga Unitaria”, que se expondrá a
continuación a través de un ejemplo:
MÉTODO DE LA CARGA UNITARIA
En la viga de la figura, se desea calcular la flecha en su punto medio C
q kg/m
C
A L/2 B
L
Se considera la viga sometida a dos sistemas de cargas:
Estado de carga 1 Estado de carga 2
la viga sometida a las cargas reales la viga sometida a una carga unitaria
aplicada en el punto medio C y en
dirección de su desplazamiento
q kg/m 1 kg
yC yC
C C
R´B RA RB
R´A
deformación real deformación virtual =
deformación real estado
de carga 1
R´A = R´B = q.L/2 Kg
RA = RB = 1/2 Kg
14

210. Sección 9.2.3: Teorema de los Trabajos Virtuales
Aplicando el Teorema de los Trabajos Virtuales, (ecuación (9.17)), a la viga del
estado de carga 2, a la cual se le ha dado una deformación virtual que sea la misma
que la deformación real que tendrá la viga con el estado de carga 1, se tendrá:
L
V y .V y´
M .M ´ M .M ´
L L
∑ Fi .δ + ∑ Ri .∆ = β y .∫
´
i
´
i
G. A
.dx + ∫ z z .dx ≅ ∫ z z .dx
E .I z E .I z
0 0 0
(se desprecia el trabajo interno debido a las fuerzas cortantes Vy, por ser de pequeño
valor con respecto al producido por los momentos flectores Mz, (ver 2.9.1 apartado
D))
siendo: 1
Fi = 1 Kg Ri = R A , R B = Kg δ i´ = y C ∆´i = 0
2
1 q.L x
0− x− L/2 Mz = .x Mz =
´
.x − q.x.
2 2 2
1 L q.L x
L/2− x− L M z = .x − 1.( x − ) M ´z = .x − q.x.
2 2 2 2
y sustituyendo todos estos valores:
L/2
1 ⎛ q.L x⎞ ⎛1 L ⎞ ⎛ q.L x⎞
L
∫ .x.⎜
2 ⎝ 2
.x − q.x. ⎟.dx + ∫ ⎜ .x − 1.( x − ) ⎟.⎜
2⎠ L/2⎝
2 2 ⎠⎝ 2
.x − q.x. ⎟.dx
2⎠
1. y C + 0 = 0
E .I z
5.q.L4
y operando: yC =
384 .E .I z
15

211. Tema 9: Solicitaciones Combinadas
9.3.- FLEXIÓN Y TRACCIÓN-COMPRESIÓN COMBINADAS
Sea el caso de un elemento estructural sometido, a las vez, a las solicitaciones: N, Vy,
Vz, My, Mz
z
Vz
N
G
x
Mz
My
L
Vy
Fig.9.11 y
Cálculo de Tensiones:
Se calcularán aplicando el Principio de Superposición:
TRACCIÓN-COMPRESIÓN: (N) → σx (ver sección 4.2)
FLEXIÓN SIMPLE: (Vy, Vz) → τ (ver secciones: 5.4.2, 5.4.3 y 5.4.4)
(My, Mz) → σ (ver sección: 5.4.1)
σ x = σ x ( N ) + σ x (M y , M z )
τ = τ (V y , Vz )
Cálculo del Eje Neutro:
La ecuación del eje neutro, será: σ x = 0 → σ x = σ x ( N ) + σ x (M y , M z ) = 0
Observación: El eje neutro ya no pasará por G y el punto de σmax será el más alejado del
mismo.
n
G
z
n
σmax
y
Fig.9.12
16

212. Sección 9.3: Flexión y Tracción-Compresión combinadas
Cálculo de Deformaciones:
Se podrán calcular aplicando igualmente el Principio de Superposición, empleando para
ello las fórmulas obtenidas para el cálculo de las deformaciones en los capítulos
correspondientes:
TRACCIÓN-COMPRESIÓN: (N) → ∆L (ver sección: 4.3)
FLEXIÓN SIMPLE: (Vy, Vz, My, Mz) → Giros:θy, θz, Flechas: y, z (ver secciones:
6.2, 6.3, 6.4)
o bien a través del Teorema de Castigliano o el de los Trabajos Virtuales:
A- Por el Teorema de Castigliano:
U = U ( N ) + U (V y ) + U (Vz ) + U ( M y ) + U ( M z )
y despreciando los términos debidos a las fuerzas cortantes Vy y Vz, quedará:
∂N ∂M y ∂M z
N. M y. L M z.
∂U ∂Fi ∂Fi ∂Fi
L L
∂Fi ∫
δi = = .dx + ∫ .dx + ∫ .dx
0
E. A 0
E .I y 0
E .I z
B- Por el teorema de los Trabajos Virtuales:
despreciando igualmente los términos debidos a las fuerzas cortantes Vy y Vz,
quedará:
´
N .N ´
L
M .ML
M .M ´
L
∑ Fi .δ + ∑ Ri .∆ = ∫
i
´ ´
i
E. A
.dx + ∫ y y .dx + ∫ z z .dx
E .I y E.I z
0 0 0
17

213. Tema 9: Solicitaciones Combinadas
9.3.1- CASO PARTICULAR: TRACCIÓN-COMPRESIÓN EXCÉNTRICA
La Tracción-Compresión excéntrica es un caso particular de la Flexión + Tracción-
Compresión combinadas visto en el apartado anterior.
Caso particular 1º:
Barra sometida a Tracción-Compresión excéntrica, actuando sobre uno de los ejes
principales de inercia de la sección transversal (Izy = 0):
a
z F.e z
G F G N=F
e x x
Mz = F.e
F F
F
L x b
y Fig.9.13 y
los ejes y, z son ejes principales de inercia → Izy = 0
a
Cálculo de las tensiones:
N F G
TRACCIÓN (N): σx = = x
A A
b
a
M z . y F .e. y G x
FLEXIÓN (Mz): σx = =
Iz Iz
b
Aplicando el Principio de Superposición , la tensión total será:
F F .e. y
σ x = σ x ( N ) + σ x (M z ) = +
A Iz
n
a a a
n
yn yn n
yn
G x G x G x
b b b
si σ a ( N ) > σ a ( M z ) si σ a ( N ) = σ a ( M z ) si σ a ( N ) < σ a ( M z )
18

214. Sección 9.3.1: Caso particular: Tracción-Compresión excéntrica
Cálculo del eje neutro:
F F .e. yn Iz i2
σ x = σ x ( N ) + σ x (M z ) = + =0 → yn = − =− z
A Iz A.e e
Iz
siendo i z2 = " radio de inercia"
A
Observaciones:
• La posición del eje neutro no depende del valor de la carga F aplicada
• La posición del eje neutro depende de la excentricidad “e” con la que se aplique
la carga F y ocurrirá que:
si: e ↑ (aumenta) ⇒ yn ↓ (disminuye) y viceversa:
si: e ↓ (disminuye) ⇒ yn ↑ (aumenta)
• El eje neutro estará del lado opuesto al punto de aplicación de la carga (ello es
debido al signo menos de la fórmula obtenida)
n n
yn
G
z
e
F
y
Caso particular 2º:
Barra sometida a Tracción-Compresión excéntrica, actuando fuera de los ejes
principales de inercia de la sección transversal (Izy = 0):
F.ez
z F.ey z
x
ez F
G G
x Mz = F.ey
ey N=F
F F
F
L x My = F.ez
y Fig.9.14 y
Cálculo de las tensiones:
N F
TRACCIÓN (N): σx = =
A A
M z . y M y .z F .e y . y F .e z .z
FLEXIÓN (Mz, My): σx = + = +
Iz Iy Iz Iy
19

215. Tema 9: Solicitaciones Combinadas
Aplicando el Principio de Superposición , la tensión total será:
F F .e y . y F .ez .z
σ x = σ x ( N ) + σ x (M z , M y ) = + + (9.21)
A Iz Iy
Cálculo del eje neutro:
F F .e. yn F .ez .z n
σ x = σ x ( N ) + σ x (M z , M y ) = + + = 0 ( dividiendo por F )
A Iz Iy
1 e y . y n ez . z n
+ + = 0 ( dividiendo el deno min ador por A)
A Iz Iy
1 e .y e .z e .y e .z
+ y n + z n = 0 → 1+ y 2 n + z 2 n = 0
A Iz Iy iz iy
A A A
Para dibujar el eje neutro se hallarán sus puntos de intersección con los ejes
coordenados
n
i z2
yn zn = 0 → yn = −
G ey
zn z 2
(9.22)
n ey iy
yn = 0 → zn = −
ez F ez
y
Observaciones:
• La posición del eje neutro no depende del valor de la carga F aplicada, pero sí
depende de la excentricidad con la que actúe dicha carga.
• Si la carga F se aplica en el punto 1, de excentricidad ey1, el eje neutro será el
n1n1, siendo por lo visto anteriormente: yn1= - i2z / ey1.
Si la carga F se aplica en el punto 2, de excentricidad ez2, el eje neutro será el
n2n2, siendo por lo visto anteriormente: zn2= - i2y / ez2.
Si la carga F se aplica en un punto cualquiera de la recta r, que une los puntos 1
y 2, se podrá descomponer en sus dos componentes: F1 y F2, aplicadas en los
puntos 1 y 2 respectivamente y según el Principio de Superposición, su efecto
será la suma de los efectos que producirán, actuando por separado, las cargas
componentes F1 y F2. Según ello la línea neutra pasará necesariamente por el
punto 3, intersección de los ejes neutros n1n1 y n2n2
n2
n1 3 n1
yn1 r
zn2 G ez2 2 1 2
(F2) z
ey1 F1
F F2
1 (F1) F
n2
y
20

216. Sección 9.3.1: Caso particular: Tracción-Compresión excéntrica
NÚCLEO CENTRAL:
Dependiendo de la posición del punto de aplicación de la carga F, el eje neutro podrá
cortar o no a la sección transversal. En función de ello se define como Núcleo Central:
“la zona de la sección transversal donde podrá aplicarse la carga F para que el eje
neutro no corte a la sección”
n
n
Núcleo Central Núcleo Central
G G
n z z
F n F
y Fig.9.15.a y Fig.9.15.b
Primer caso: F se aplica dentro del Núcleo Central ⇒ El eje neutro no corta a la
sección ⇒ Todos los puntos de la sección trabajan a Tracción (σx >0) o a Compresión
(σx <0)
Segundo caso: F se aplica fuera del Núcleo Central ⇒ El eje neutro corta a la sección
⇒ Hay parte de la sección que trabaja a Tracción (σx >0) y otra parte a Compresión (σx
<0).
Se calculará a continuación el Núcleo Central para dos casos frecuentes de secciones
transversales:
A.-SECCIÓN CIRCULAR
Se situa el eje neutro n-n tangente al círculo, es decir haciendo: yn = R. Para que ello
ocurra, la excentricidad ey, con la que habrá que aplicar la carga será:
n n iz2
yn = − (ver 9.22)
ey
yn = R
G π .R 4
ey z
Iz 4
F iz2 π .R 2 = R
de donde : e y = − =− A =−
yn yn −R 4
y Fig.9.16.a
Y por simetría de la figura se podrá concluir diciendo que: “el Núcleo Central de una
sección circular es un círculo, con el mismo centro y con radio R/4”
21

217. Tema 9: Solicitaciones Combinadas
R
G
G
R/4
núcleo
central Fig.9.16.b
B.-SECCIÓN RECTANGULAR
Se sitúa el eje neutro n1-n1 en el borde superior del rectángulo, es decir haciendo:
yn = -h/2. Para que ello ocurra, la excentricidad ey1, con la que habrá que aplicar la carga
será:
n2
n1 3 n1
iz2
yn = h/2 yn = − (ver 9.22)
e y1
zn = b/2 ez2 2 b.h3
z h
ey1 Iz 12
iz2 b.h = h
1 de donde : e y1 = − =− A =−
r yn yn −h / 2 6
n2 y
b
Fig.9.17.a
Se sitúa ahora el eje neutro n2-n2 en el borde izquierdo del rectángulo, es decir
haciendo:
zn = -b/2. Para que ello ocurra, la excentricidad ez2, con la que habrá que aplicar la carga
será:
h.b 3
2 2
Iy 12
iy iy A =− b.h = b
zn = − (ver 9.19) → de donde : e z 2 = − =−
ez 2 zn zn −b/2 6
Si se traza ahora la recta r que pasa por los puntos 1 y 2 y por lo visto anteriormente: “si
la carga externa F se aplica sobre la recta r, entre dichos puntos, el eje neutro pasará por
el punto 3 de intersección de los ejes neutros: n1-n1 y n2-n2, sin cortar al interior del
rectángulo. Repitiendo este procedimiento a los otros bordes del rectángulo resultará
que: “el Núcleo Central de una sección rectangular es un rombo, con el mismo centro y
de semidiagonales h/6 y b/6”
22

218. Sección 9.4: Flexión y Torsión combinadas
núcleo
central
h/6
z h
y b/6
b
Fig.9.17.b
9.4- FLEXIÓN Y TORSIÓN COMBINADAS
Sea el caso de un elemento estructural sometido, a las vez, a las solicitaciones: N, Vy,
Vz, T, My, Mz
z
Vz
T
G
x
Mz
My
Vy
Fig.9.18 y
Cálculo de Tensiones:
Se calcularán aplicando el Principio de Superposición:
TORSIÓN: (T) → τ (ver secciones: 8.2, 8.3, 8.4 y 8.5)
FLEXIÓN SIMPLE: (Vy, Vz) → τ (ver secciones: 5.4.2, 5.4.3 y 5.4.4)
(My, Mz) → σ (ver sección: 5.4.1)
σ x = σ x (M y , M z )
r r r
τ = τ (V y , Vz ) + τ (T )
Observación: en la mayoría de los casos τ (Vy, Vz) << τ (T) y se suelen despreciar,
teniendo en cuenta sólo entonces: τ (T)
23

219. Tema 9: Solicitaciones Combinadas
Cálculo de Deformaciones:
Se podrán calcular aplicando igualmente el Principio de Superposición, empleando para
ello las fórmulas obtenidas para el cálculo de las deformaciones en los capítulos
correspondientes:
TORSIÓN: (T) → θx ,ϕx (ver secciones: 8.2, 8.3, 8.4, 8.5)
FLEXIÓN SIMPLE: (Vy, Vz, My, Mz) → Giros:θy, θz, Flechas: y, z (ver secciones:
6.2, 6.3, 6.4)
o bien a través del Teorema de Castigliano o el de los Trabajos Virtuales:
A.-Por el Teorema de Castigliano:
U = U (V y ) + U (Vz ) + U (T ) + U ( M y ) + U ( M z )
y despreciando los términos debidos a las fuerzas cortantes Vy y Vz, quedará:
∂T ∂M y ∂M z
T. L M y. L M z.
∂U ∂Fi ∂Fi ∂Fi
L
∂Fi ∫
δi = = .dx + ∫ .dx + ∫ .dx
0
G.I t 0
E .I y 0
E .I z
B.-Por el teorema de los Trabajos Virtuales:
despreciando igualmente los términos debidos a las fuerzas cortantes Vy y Vz,
quedará:
L
T .T ´
L
M .M ´ L
M .M ´
∑ Fi .δ i´ + ∑ Ri .∆´i = ∫G.I t
.dx + ∫ y y .dx + ∫ z z .dx
E.I y E .I z
0 0 0
24

220. Sección 9.5: Flexión y compresión combinadas en piezas mu esbeltas
muy
9.5-FLEXIÓN Y COMPRESIÓN COMBINADAS EN PIEZAS MUY ESBELTAS
9.5.1-INTRODUCCIÓN
En el caso de piezas muy esbeltas solicitadas a flexión-compresión combinadas, habrá
que tener en consideración nuevas precisiones a lo ya visto anteriormente, en base a los
siguientes hechos:
P P
F F
y0 y0
y
x
x
Mz0
Mz0 Mz0 Mz
Mz
Fig. 10.29.a Fig. 10.29.b
En la fig.10.29.a., se representa una viga sometida a la carga F de compresión y a la
carga lateral P que produce flexión. Se indica así mismo la elástica y0 y el diagrama de
momentos flectores Mz0 debidos a la carga P. Tanto la elástica como el diagrama de
momentos flectores los podremos obtener con los conocimientos estudiados hasta ahora.
En la fig.10.29.b., se representa de nuevo la misma viga con las mismas cargas, pero se
ha tenido en cuenta que la elástica producida por la carga de flexión P se ha visto
amplificada por la carga de compresión F, dando lugar a la elástica y. Así mismo
ocurrirá con el diagrama de momentos flectores.
Así pues ocurrirá:
y0 , Mz0 → elástica y momento flector debidos sólo a la carga lateral P (Tema 9)
y, Mz → elástica y momento flector debidos a la carga lateral P y amplificados
debido a la carga de compresión F (Tema 10)
Observación: La amplificación de la flexión debido a la carga de compresión, es un
efecto que habrá que tener muy en cuenta sobre todo en el caso de piezas muy esbeltas y
sometidas a cargas grandes, pues es en estos casos donde dicha amplificación toma una
importante relevancia. En el resto de los casos: piezas no muy esbeltas o piezas muy
esbeltas pero con cargas no muy grandes, que son la mayoría de los casos que se nos
darán en la práctica, no será necesario su consideración.
25

221. Tema 9: Solicitaciones Combinadas
9.5.2-ESTUDIO DE LA FLEXIÓN-COMPRESIÓN EN PIEZAS MUY
ESBELTAS SOMETIDAS A GRANDES CARGAS
P
F
x
y
x
y
Fig. 10.30
Ecuación de la elástica amplificada
La ecuación diferencial de la línea elástica será:
d2y M
2
=− z siendo : M z = M z0 + F . y
dx E.I z
M z0 : momento flector debido sólo a la c arg as laterales
d2y M 0 + F.y d2y F M0
=− z → + .y = − z
dx 2 E .I z dx 2 E.I z E.I z
ecuación diferencia l de la elástica
sustituyendo:
(10.35)
F d2y M z0
haciendo: k =2
→ + k z .y = −
2
(10.36)
dx 2
z
E .I z E .I z
ecuación diferencia l de la elástica
La solución de la ecuación diferencial será de la forma:
y = C1 .sen k z .x + C 2 . cos k z .x + y p (10.37)
en donde yp, es la solución particular y será una expresión de la misma forma que Mz0
Ejemplo: Resolvamos la ecuación diferencial para el siguiente caso concreto
q
F
L x
ymax
RA= q.L/2 y = y(x) RB= q.L/2
y
Fig. 10.31
26

222. Sección 9.5: Flexión y compresión combinadas en piezas muy esbeltas
q. L x2
M z0 = . x − q. → y p = C3 .x 2 + C 4 .x + C5 ( del mismo grado que M z0 )
2 2
la ecuación de la elástica será : y = C1 .sen k z .x + C 2 . cos k z .x + C3 .x 2 + C 4 .x + C5 (10.38)
Cálculo de las constantes C3, C4, C5 :
⎫
y = C1 .sen k z .x + C2 .cos k z .x + C3 .x 2 + C4 .x + C5 ⎪
⎪
dy ⎪ llevando estos valores a la ecuación
= C1.k z .cos k z .x − C2 .k z .sen k z .x + 2.C3 .x + C4 ⎬ →
dx ⎪ diferencial de la elástica (10.36) quedará:
2
d y ⎪
= −C1 .k z2 .sen k z .x − C2 .k z2 .cos k z .x + 2.C3 ⎪
dx 2
⎭
−C1.k z2 .sen k z .x − C2 .k z2 .cos k z .x + 2.C3 + k z2 .(C1.sen k z .x + C2 . cos k z .x + C3 .x 2 + C4 .x + C5 ) =
1 ⎛ q.L q ⎞
=− .⎜ .x − .x 2 ⎟ y operando :
E .I z ⎝ 2 2 ⎠
⎛ q ⎞ 2 ⎛ q.L ⎞
(k z2 .C3 ).x 2 + ( k z2 .C4 ).x + (2.C3 + k z2 .C5 ) = ⎜ ⎟ .x − ⎜ ⎟ .x e igualando términos :
⎝ 2.E.I z ⎠ ⎝ 2.E.I z ⎠
q − q.L −q
C3 = 2 C4 = 2 C5 = 4
k z .2.E.I z k z .2.E .I z k z .E.I z
Cálculo de las constantes C1, C2 : poniendo ecuaciones de contorno de la elástica:
q
x=0 → y = 0 ⇒ C2 = 4
k .E .I z
z
q ⎛ 1 − cos k z .L ⎞
x=L → y = 0 ⇒ C1 = .⎜ ⎟
k .E.I z ⎜ sen k z .L ⎟
4
z ⎝ ⎠
y sustituyendo finalmente todas las constantes calculadas en la ecuación de la elástica
10.38. quedará:
q ⎡1 − cos k z .L k2 ⎤
y= 4
.⎢ .sen k z .x + cos k z .x − 1 − z .( L.x − x 2 ) ⎥ (10.39)
k z .E .I z ⎣ sen k z .L 2 ⎦
”ecuación de la línea elástica amplificada” (para el ejemplo de la fig.10.31)
Cálculo de la flecha máxima
La flecha máxima, para el ejemplo que se está analizando, se dará en x = L/2 y valdrá:
L q ⎡1 − cos k z .L L L k z2 ⎛ L2 L2 ⎞ ⎤
ymax = y( x = ) = 4 .⎢ .sen k z . + cos k z . − 1 − . ⎜ − ⎟ ⎥
2 k z .E.I z ⎣ sen k z .L 2 2 2 ⎝ 2 4 ⎠⎦ 27
haciendo : u =
k z .L
→ ymax =
5.q.L
.
4 (
24. sec u − 1 − u
2
2 ) "flecha máxima amplificada "
2 384.E .I z 3.u 4

223. Tema 9: Solicitaciones Combinadas
Observaciones:
1.- La carga F de compresión a amplificado la elástica producida por la carga lateral q
En efecto: En el ejemplo visto anteriormente, si la viga sólo hubiese estado sometida a
la carga lateral q, (ver fig 10,32), el valor de la flecha máxima que se obtendría sería:
q
5.q.L4
y max =
0
y0max 384 .E.I z
y0
Fig. 10.32 (valor obtenido de Tablas)
En el caso de considerar también la carga de compresión F (ver fig.10.33), el valor
obtenido para la flecha máxima ha sido:
q ⎛ u2 ⎞
24.⎜ sec u − 1 −
⎜ ⎟
⎟
F 5.q.L4 2
ymax y max = . ⎝ ⎠
0
384.E.I z 3.u 4
y
y
Fig. 10.33
Comparando ambos valores se puede poner:
⎛ u2 ⎞
24. ⎜ sec u − 1 − ⎟
2 ⎠
ymax = ymax . ⎝
0
4
= k2 . ymax
0
3.u
⎛ u2 ⎞
24. ⎜ sec u − 1 − ⎟
⎝ 2 ⎠ "coeficiente de amplificación de la flecha máxima
siendo: k2 = 4
3.u producida por la carga F de compresión"
Momentos flectores amplificados
Conocida ya la elástica amplificada, el momento flector amplificado se podrá obtener
por dos procedimientos:
1) M z = M z0 + F . y (10.40)
d2y M d2y
2) 2
=− z → M z = − E .I z . (10.41)
dx E .I z dx 2
28

224. Sección 9.5: Flexión y compresión combinadas en piezas muy esbeltas
Así para el ejemplo que nos ocupa, la elástica amplificada viene dada por la ecuación
10.39 y quedará:
M z = M z0 + F . y =
⎛ q.L q ⎞ q ⎡1 − cos k z .L k2 ⎤
=⎜ .x − .x 2 ⎟ + F . 4 .⎢ .sen k z .x + cos k z .x − 1 − z .( L.x − x 2 ) ⎥ =
⎝ 2 2 ⎠ k z .E.I z ⎣ sen k z .L 2 ⎦
y operando
q ⎡1 − cos k z .L ⎤
Mz = .
2 ⎢
.sen k z .x + cos k z .x − 1⎥ " momento flector amplificado"
k z ⎣ sen k z .L ⎦
(10.42)
Cálculo del momento flector máximo
El momento flector máximo, para el ejemplo que se está analizando, se dará en x = L/2
y valdrá:
L q ⎡1 − cos k z .L L L ⎤
M z max = M z ( x =) = 2 .⎢ .sen k z . + cos k z . − 1⎥
2 k z ⎣ sen k z .L 2 2 ⎦
k .L q.L2 2.(1 − cos u ) "momento flector máximo
haciendo : u = z → M z max = . 2
2 8 u .cos u amplificado"
Observaciones:
1.- La carga F de compresión a amplificado el momento flector producido por la carga
lateral q
En efecto: En el ejemplo visto anteriormente, si la viga sólo hubiese estado sometida a
la carga lateral q, (ver fig 10.34), el valor del momento flector máximo que se obtendría
sería:
q
L
q.L2
M z0max =
x 8
M0max
(valor obtenido de Tablas)
0 0
Mz Mz
Fig. 10.34
29

225. Tema 9: Solicitaciones Combinadas
En el caso de considerar también la carga de compresión F (ver fig.10.35), el valor
obtenido para el momento flector máximo ha sido:
q
F
L
x
Mzmax
Mz M0z
Fig. 10.35 Mz
q.L2 2.(1 − cos u )
M z max = . 2
8 u . cos u
comparando ambos valores se puede poner:
2.(1 − cos u )
M z max = M zomax . 2
= k3 .M z0max
u .cos u
2.(1 − cos u ) "coeficiente de amplificación del momento flector
siendo : k3 =
u 2 .cos u máximo, debido a la carga F de compresión"
Cálculo de las tensiones amplificadas
Al amplificarse el momento flector se verán amplificadas las tensiones que él produce,
así para el ejemplo que se está estudiando sería:
0
F M z .v y F (k3 .M z ).v y F M 0 .v
σ total = σ ( N ) + σ ( M z ) = + = + = + k3 . z y = σ + k3 .σ 0
f
A Iz A Iz A Iz
2.(1 − cos u ) "coeficiente de amplificación de las tensiones debidas a la flexión
siendo: k3 =
u 2 .cos u producido por la carga F de compresión"
(es el mismo coeficiente que el de amplificación de los momentos flectores)
30

226. Sección 9.6: Introducción al dimensionamiento a resistencia de vigas metálicas sometidas a solicitaciones
combinadas
9.6-INTRODUCCIÓN AL DIMENSIONAMIENTO A RESISTENCIA DE VIGAS
METÁLICAS SOMETIDAS A SOLICITACIONES COMBINADAS .(Normativa
DB-SE-A)
A.- RESISTENCIA DE LAS SECCIONES
1.-Caso de Flexión y Axil: N, Mz, My
Criterio elástico de dimensionamiento
Las fórmulas a aplicar serán: N* Mz *
M*
+ + ≤1
y
(9.23)
N pl ,d M zel ,d M yel ,d
Criterio plástico de dimensionamiento
N* M z* M* (9.24)
Las fórmulas a aplicar serán: + + y
≤1
N pl ,d M pl ,d M pl ,d
Observación:
En los casos en que no existiesen algunas de las solicitaciones: N, Mz, My, las fórmulas
a utilizar serían las mismas, sin más que hacer cero la solicitación que no actúe
2.-Caso de Flexión, Axil y Cortante: N, Mz, My, Vy, Vz
El estudio se hará indistintamente para las cortaduras: Vy o Vz y la denominaremos en
general: V
1 1 f
Siempre que: V * ≤ .V pl , d = . Av . yd → no habrá que hacer mas comprobaciones
2 2 3
tan sólo las correspondientes al caso 1º (sin cortantes)
Los valores a considerar para el área Av de la sección son los siguientes:
• Secciones macizas de gran espesor: rectangulares, circulares,…….
Av = A (área de la sección)
• Perfiles abiertos de pequeño espesor: IPE, HEB, UPN,……….
Con cortadura Vy: Av = Área del alma del perfil
Con cortadura Vz: Av = Área de las alas del perfil
• Perfiles cerrados de pequeño espesor circulares:
Av = A.2/π
31

227. Tema 9: Solicitaciones Combinadas
En el caso de que no se cumpliese lo anterior, es decir:
1 1 f yd
V * > .Vpl ,d = . Av .
2 2 3
habría que hacer una nueva comprobación combinando el Momento flector con la
Fuerza Cortante (ver Normativa DB-SE-A)
3.-Otros casos de combinaciones
Su estudio es objeto de otras asignaturas específicas. (Ver normativa)
B.- RESISTENCIA DE LAS BARRAS
Al considerar ahora la barra en su conjunto se tendrán que hacer nuevas
comprobaciones, pero estas comprobaciones son objeto de otras asignaturas específicas.
(Ver normativas)
32

228. Tema 10: Pandeo
Tema 10 : PANDEO
x
Ncr
(1) (2) π 2 .E .I z
N cr =
L y L2
x
y
1

229. Tema 10: Pandeo
10.1.- INTRODUCCIÓN
Los diferentes elementos que conforman una estructura pueden “fallar” por diferentes
motivos, dependiendo de los materiales utilizados, tipos de cargas, ligaduras y apoyos.
Muchos de estos tipos de “fallos” se podrán evitar, dimensionando dichos elementos de
tal forma, que las tensiones y deformaciones máximas que se produzcan permanezcan
dentro de los límites admisibles y así se efectuarán los dimensionamientos a Resistencia
y a Rigidez, estudiados en los temas precedentes.
Pero existen otros tipos de “fallos”, como es el “fallo por inestabilidad o pandeo”, que
puede tener lugar en el caso de elementos estructurales esbeltos sometidos a
compresión. En estos casos, en el elemento puede aparecer una flexión lateral que puede
llegar a ser grande y hacer “fallar” al elemento
N N
Flexión lateral (PANDEO)
La aparición de dicha flexión lateral, su rápido crecimiento y la pérdida total de
estabilidad del elemento y el consiguiente colapso de la estructura, constituyen el
estudio del Pandeo.
Ejemplos de elementos estructurales donde puede aparecer el Pandeo:
Pandeo en las barras de las
10. Estructuras Articuladas
2.-
Pandeo en los pilares de los ESTUDIO TEÓRICO DEL PANDEO DE
edificios PIEZAS SOMETIDAS A COMPRESIÓN
Las piezas sometidas a compresión pueden agruparse en dos grupos:
• PIEZAS SIMPLES
• PIEZAS COMPUESTAS
2

230. Sección 10.2: Estudio teórico del Pandeo de piezas sometidas a compresión
1.-Las PIEZAS SIMPLES pueden estar constituidas por:
a) Un solo perfil
b) Varios perfiles o chapas unidas mediante tornillos o soldadura
• Si el enlace se hace por medio de tornillos, se deberá cumplir:
s ≤ 8.a s ≤ 15 .e
s: distancia entre ejes de uniones
a: diámetro de los agujeros
e: mínimo espesor de las piezas a unir
• Si el enlace se hace con soldadura discontinua, se deberá cumplir:
s ≤ 15 .e s ≤ 300 mm
s
s: distancia entre ejes de soldaduras
e: mínimo espesor de las piezas a unir
c) Perfiles unidos con forros discontinuos de chapa o presillas
s
3

231. Tema 10: Pandeo
En este caso se deberá cumplir: s ≤ 15.i
i: radio de giro mínimo de los perfiles a unir
2.-Las PIEZAS COMPUESTAS, lo serán, cuando no se cumplan alguno de los
supuestos anteriores.
Observación:
En este Tema se hará el estudio del Pandeo para los casos de PIEZAS SIMPLES. (El
Pandeo en Piezas Compuestas se estudia en otras asignaturas, tales como: “Estructuras
Metálicas”)
10.2.1.- CARGA CRÍTICA DE EULER
El estudio teórico del Pandeo, que es debido a Euler, se planteó como un estudio de
equilibrio.
Así, si se tiene una pieza sometida a una fuerza N de compresión y se encuentra en
equilibrio, posición (1), su equilibrio podrá ser: ESTABLE, INESTABLE o
INDIFERENTE
N N N
(1) (2) (1) (2) (1) (2)
Equilibrio Equilibrio Equilibrio
ESTABLE INESTABLE INDIFERENTE
Fig. 10.1
Equilibrio Estable: si al separarla un poco, a la pos. (2) y soltar, vuelve a la pos.(1)
Equilibrio Inestable: si al separarla un poco, a la pos. (2) y soltar, se aleja de la pos.(1)
Equilibrio Indiferente: al separarla un poco, a la pos. (2) y soltar, se queda en la pos.(2)
4

232. Sección 10.2.1: Carga crítica de Euler
El que una pieza dada adopte uno u otro tipo de equilibrio, va a depender del valor de la
carga F de compresión a la que se le someta.
Se denomina: CARGA CRÍTICA (Ncr): “al valor de la carga N de compresión que
hace que se alcance el EQUILIBRIO INDIFERENTE ”
Así pues se tendrá:
• si N = Ncr → Equilibrio Indiferente
• si N < Ncr → Equilibrio Estable
• si N > Ncr → Equilibrio Inestable
Naturalmente se deberá hacer trabajar a las piezas con N < Ncr, para que se encuentren
siempre en equilibrios estables.
Cálculo del valor de la Carga Crítica de Euler: Ncr
Fue Euler el que calculó dicho valor.
Considérese una pieza (columna), recta, con sus extremos articulados y sometida a una
carga de compresión centrada, de valor la carga crítica Ncr.
x Por lo visto anteriormente, la columna se encontrará en la
posición (1) en equilibrio INDIFERENTE y por tanto, si
Ncr la separamos un poco a la posición (2), permanecerá en
dicha posición.
Si N = Ncr → Equilibrio Indiferente.
(1) (2)
L y La ecuación diferencial de la Elástica en la posición (2)
será, (ver 6.2):
Fig. 10.2 d2y
x M
=− z siendo : M z = N cr . y
y dx 2
E .I z
d2y d 2 y N cr
E .I z . = − M z = − N cr . y → + . y = 0 ecuación diferencial línea elástica
dx 2 dx 2 E.I z
N cr d2y
haciendo : k z2 = (10.1) → 2
+ k z2 . y = 0
E .I z dx
la solución general de esta ecuación diferencial es de la forma : y = C1.senk z .x + C2 .cos k z .x
Cálculo de las cons tan tes C1 y C2 :
x=0 → y = 0 ⇒ C2 = 0
x=L → y = 0 ⇒ C1.senk z .L = 0 → C1 = 0 ⇒ y = 0 elástica rectilínea ( pos.1)
→ senk z .L = 0 ⇒ k z .L = n.π ( n = 1, 2, 3,.....)
n.π n 2 .π 2
kz = → k z2 = (10.2) igualando las exp resiones (10.1) y (10.2) :
L L2
5

233. Tema 10: Pandeo
N cr n 2 .π 2 π 2 .E .I z
= → N cr = n 2 .
E .I z L2 L2
π 2 .E .I z
El menor de estos valores se obtendrá para n = 1 y será: N cr = (10.3)
L2
Observaciones:
1.-Si el pequeño desplazamiento que se da a la columna para llevarla a la posición (2) se
hiciera en el plano XZ, la expresión de la carga crítica FC sería:
π 2 .E .I y
N cr =
x x L2
Ncr Ncr
(1) (2) π 2 . E .I z (1) (2) π 2 .E .I y
N cr = z N cr =
L y L2 L L2
z
x x
y y
Fig. 10.3
¿En cual de los dos planos pandeará finalmente la columna?
Conclusión: “ Una columna pandeará en el plano que presente menor rigidez a la
flexión, es decir, en el plano respecto del cual el módulo de rigidez a la flexión sea
mínimo: E.Imin “
π 2 .E .I min
Así pues la expresión de la carga crítica de Euler será: N cr = (10.4)
L2
Ejemplo:
Los ejes Y, Z son ejes principales de inercia (ejes de simetría).
x
Respecto de ellos se obtendrán: Imax, Imin
Ncr
1 1
Iy = .b.h 3 Iz = .h.b 3
12 12
si b < h → I z < I y ⇒ I min = I z
E.I min = E.I z
y
z “la columna pandeará (flexará) en el plano XY, osea
alrededor del eje Z”
y
Ncr Fig. 10.4
6

234. Sección 10.2.1: Carga crítica de Euler
2.-De la fórmula 10.4, que da la carga crítica, se obtienen las siguientes conclusiones:
π 2 .E .I min
N cr =
L2
a) “ El valor de la carga crítica Ncr depende del material del que esté fabricada la
columna: Eacero, Ehormigón, Ealuminio,…………….”
b) “ Para un material dado, el valor de Ncr no depende de la calidad del mismo, esto
es de su resistencia” ( en la fórmula de Ncr no interviene la fy ni la fu )
Ejemplo: material 1: acero tipo 1: E = 2,1.105 N/mm2; fy = 275 N/mm2
material 2: acero tipo 2: E = 2,1.105 N/mm2; fy = 350 N/mm2
Conclusión: Los dos aceros tendrán la misma carga crítica Ncr, es decir, se
comportarán igual frente al Pandeo
c) “ La carga crítica Ncr es directamente proporcional al módulo de rigidez a la
flexión: E.I “. Así pues, mejoraremos la resistencia al Pandeo, utilizando
columnas que opongan gran resistencia a la flexión, es decir, que tengan
módulos de rigidez a la flexión grandes
d) “ La carga crítica Ncr es inversamente proporcional al cuadrado de la longitud de
la columna: L2 “. Así pues cuanto mayor sea la longitud de la columna, más
posibilidades de que se alcance la carga crítica y se produzca el fallo por
Pandeo.
Ecuación de la línea elástica:
Anteriormente se vió que la solución de la integración de la ecuación diferencial de la
elástica era de la forma: y = C1.sen kz.x + C2.cos kz.x
n.π
en donde : C 2 = 0 → y = C1 .senk z .x siendo : k z = (10.2) =
L
n.π
y sustituyendo : y = C1 .sen .x ecuación línea elástica
L
Observaciones: El valor de C1 resulta indeterminado, ello es debido a haber tomado
como valor del radio de curvatura:
d2y
2
1 d y 1 dx 2
≅ en lugar de su valor exacto : = 3
r dx 2 r ⎡ 2
⎤ 2
⎛ dy ⎞
⎢1 + ⎜ ⎟ ⎥
⎢ ⎝ dx ⎠ ⎥
⎣ ⎦
Si se dan valores a n = 1, 2, 3,….., se obtienen las elásticas correspondientes a los
diferentes estados de equilibrios indiferentes:
7

235. Tema 10: Pandeo
• π π 2 .E.I min
Si n = 1 → y = C1.sen .x siendo : N cr =
L L2
x
dy L
Ncr la flecha máxima será : =0→ x=
dx 2
L π L π
y max = y ( x = ) = C1.sen . = C1.sen = C1
2 L 2 2
(1) (2)
Esta será la forma que tome la elástica cuando
L ymax
se consiga el equilibrio indiferente bajo la carga
L/2 π 2 .E.I min
y N cr =
L2
Fig. 10.5
2.π π 2 .E.I min
• Si n = 2 → y = C1 .sen .x siendo : N cr = 2 . 2
L L2
x
Ncr dy L 3 .L
la flecha máxima será : =0→ x= ,x=
dx 4 4
L 2.π L π
(1) y max = y ( x = ) = C1 .sen . = C1 .sen = C1
ymax 4 L 4 2
3L/4 3L 2.π 3 L 3π
y max = y (x = ) = C1 .sen . = C1 .sen = −C1
L 4 L 4 2
(2)
L/2 ymax Esta será la forma que tome la elástica cuando
L/4 se consiga el equilibrio indiferente bajo la carga
y
π 2 .E .I min
Fig. 10.6 N cr = 2 . 2
L2
Se tomará para el cálculo el menor de los valores de Ncr, es decir, la carga Ncr que
consiga el primer equilibrio indiferente, o sea para el valor n = 1
8

236. Sección 10.3: Estudio práctico del pandeo: Piezas sometidas a compresión
10.2.2.- INFLUENCIA DE LOS ENLACES. LONGITUD DE PANDEO
El valor obtenido para la carga crítica FC, corresponde al caso de una columna
articulada en sus extremos.
Ncr
L π 2 .E .I min
N cr =
L2
β = 1 Lk = L
Fig. 10.7
Con otros tipos de apoyos y siguiendo un proceso similar al seguido en 10.2.1, se
obtendrán los valores de FC correspondientes:
Ncr Ncr Ncr
π 2 .E .I min 2.π 2 .E .I min 4.π 2 .E .I min
L N cr = L N cr = L N cr =
4.L2 L2 L2
1 β = 0, 5 Lk = 0, 5 L
β = 2 Lk = 2.L β= ≅ 0, 7 Lk = 0, 7 L
2
Fig. 10.8 Fig. 10.9 Fig. 10.10
Con el objeto de poder utilizar una sola fórmula que englobe a los cuatro casos, se
utilizará la siguiente:
π 2 .E .I min
N cr = (10.5)
L2
k
siendo: Lk = β .L " longitud de pandeo " (10.6)
Los valores de β y por consiguiente de Lk para cada uno de los cuatro tipos de apoyos
vistos, se obtendrán comparando la fórmula general 10.5 para la carga crítica, con las
obtenidas en cada uno de ellos. Los valores están indicados en las figuras
correspondientes
9

237. Tema 10: Pandeo
Longitud de pandeo de barras canónicas: Lk
Condiciones empotrada empotrada biempotrada
biarticulada biempotrada
de extremo articulada libre desplazable
Lk 1,0.L 0,5.L 0,7.L 2,0.L 1,0.L
Concepto físico de la longitud de pandeo:
La longitud de pandeo de una barra es: “la longitud que debería tener una barra,
articulada en ambos extremos, equivalente a la dada (mismo material y sección ), para
que tuviese la misma carga crítica Ncr, que la barra dada “
x
Ncr Ncr Ncr Ncr
Ncr
L L L ymax Lk = 0,5L
ymax Lk = L
Lk = 2L ymax
y
Fig. 10.11 Fig. 10.13
Fig.10.12
Ncr
Lk = 0,7.L
ymax
L
Fig.10.14
10

238. Sección 10.3: Estudio práctico del pandeo: Piezas sometidas a compresión
10.2.3.- TENSIÓN CRÍTICA DE EULER. CONCEPTO DE ESBELTEZ
Se denomina TENSIÓN CRÍTICA de Euler: “a la tensión de compresión de una
columna cuando sobre ella actúa la carga crítica Ncr “
N cr
σ cr = (10.7)
A
Sustituyendo FC por su valor dado en 10.5, quedará:
I min
Ncr π 2 .E.I min π .E.
2
A = π .E.imin = π .E = π .E
2 2 2 2
σ cr = = = (10.8)
A L2 . A L2 L2 ⎛ Lk ⎞
2
λ2
⎜ i ⎟
k k k
⎝ min ⎠
Lk
siendo: λ= " esbeltez de una columna " (10.9)
imin
Representando gráficamente, en unos ejes coordenados, la ecuación 10.8 que da la
tensión crítica de Euler en función de la esbeltez, se obtiene el siguiente diagrama:
σcr
π 2 .E
σ cr = " curva de Euler "
λ2
σcr2
σcr1
λ2 λ1 λ
Fig.10.15
Del análisis del diagrama se deduce que a medida que disminuimos la esbeltez λ de la
columna (λ2 < λ1 ) la tensión crítica σC aumenta (σcr2 > σcr1 ), es decir aumenta la
capacidad de la columna para resistir mas cargas sin que se produzca el Pandeo.
Conclusión: Para mejorar el comportamiento de una columna, de longitud dada, frente
al Pandeo, será preciso disminuir su esbeltez λ. ¿Cómo?. Si la longitud L nos viene
impuesta, en función de la ecuación 10.9 que da la esbeltez, habrá que aumentar el radio
de inercia mínimo imin.
Lk
λ= si imin ↑ ⇒ λ ↓
imin
11

239. Tema 10: Pandeo
El aumento de imin sin modificar el área A, se consigue aumentando el momento de
inercia Imin, osea alejando el material todo lo posible del centro de gravedad de la
sección
I min
i min = si I min ↑ ⇒ imin ↑
A
Esta es la razón, por ejemplo, por la que las columnas de sección hueca son mejores, a
efectos de pandeo, que las macizas del mismo área
sección 1 sección 2
G G
A1, Imin1 A2 = A1, Imin2
Fig.10.16
I min 2 > I min 1 → imin 2 > imin 1 → λ2 < λ1 → σ c 2 > σ c1 → Fc 2 > Fc1
⇒ la sec ción 2 se comportará mejor al pandeo que la sec ción 1
12

240. Sección 10.3: Estudio práctico del pandeo: Piezas sometidas a compresión
10.2.4.- LÍMITES DE APLICACIÓN DE LA FÓRMULA DE EULER
El diagrama de la fig.10.15, que representa la curva de la tensión crítica de Euler, sólo
va a ser válida hasta un cierto punto P, que corresponde a una esbeltez λlim, que es la
esbeltez para la cual: σcr (tensión crítica) = fy (tensión del límite elástico).
σcr
π 2 .E
σ cr = 2 " curva de Euler "
λ
fy P
λlim λ
Fig.10.17
Ello es debido a que en la deducción de la fórmula para la obtención de la carga crítica
Ncr, se utiliza la ecuación diferencial de la elástica y ésta sólo es aplicable para los casos
en que E = cte o lo que es lo mismo cuando σ ≤ fy ( sección 3.5. diagrama tensiones-
deformaciones). Además, al alcanzarse la tensión del límite elástico, el fallo se
produciría por haberse alcanzado la resistencia a la compresión de la sección.
En la Fig. 10.18 se representa la curva de pandeo de Euler y los modos de fallo
σ
Fallo por haber rebasado
el límite elástico
fy P
Fallo por
pandeo
Curva de pandeo
de Euler
λlim λ
Figura 10.18
13

241. Tema 10: Pandeo
Así pues tendremos que para poder utilizar la curva de Euler se habrá de verificar:
π 2 .E π 2 .E π 2 .E
σ cr ≤ f y → ≤ fy → λ≥ ⇒ λlim = (10.10)
λ2 fy fy
• para esbelteces: λ ≥ λlim → SI se podrá aplicar la curva de Euler
• para esbelteces: λ ≤ λlim → NO se podrá aplicar la curva de Euler
Los valores de λlim para los aceros más utilizados en la construcción son:
Acero fy (N/mm2) λlim
S235 235 93,9
S275 275 86,8
S355 355 76,4
La curva de pandeo expresada en la fig.10.18 puede ser redibujada de forma
adimensional, dividiendo la tensión crítica de Euler entre el límite elástico: (σ / fy ) y la
esbeltez entre la esbeltez límite: (λ / λlim), dando lugar a la siguiente curva de Pandeo
adimensional
σ/f
σ/fy
P P
1 1
1 1 λ/λ
λ/λ lim
Figura 10.19
La ventaja de este gráfico es que puede aplicarse a barras de diferentes esbelteces y
resistencias
14

242. Sección 10.3: Estudio práctico del pandeo: Piezas sometidas a compresión
10.3.- PANDEO REAL: ESTUDIO PRÁCTICO DEL PANDEO EN PIEZAS DE
ACERO SOMETIDAS A COMPRESIÓN
10.3.1.- INTRODUCCIÓN
El comportamiento real de los pilares difiere del estudio teórico e ideal que acabamos
de hacer. Ello es debido a las diversas imperfecciones del pandeo “real” que no se han
tenido en cuenta en el estudio teórico, tales como:
• Falta de rectitud inicial del eje del pilar
• Cargas axiales no aplicadas exactamente en el centro de gravedad de la sección
transversal del pilar
• Tensiones residuales producidas en la fabricación del pilar, bien por el proceso
de laminación o por las soldaduras
• Otras
Así estudios experimentales de pilares reales proporcionan los resultados que se
muestran en la siguiente figura:
σ
Esbeltez media Esbeltez elevada
P
fy
Punto de
inflexión
λlim λ
Figura 10.20
Comparado con las curvas teóricas, el comportamiento real muestra mayores
dispersiones en el intervalo de esbelteces medias que en el intervalo de esbelteces
elevadas. En la zona de esbelteces medias (que representa a la mayoría de los pilares), el
efecto de las imperfecciones es significativo y debe de ser tenido en cuenta. La mayor
reducción en el valor teórico se produce en la región de la esbeltez límite λlim.
La curva límite inferior se ha obtenido de un análisis estadístico de los resultados de los
ensayos y representa el límite seguro para la carga.
15

243. Tema 10: Pandeo
Un pilar puede ser considerado de esbeltez elevada si su esbeltez es mayor que la
correspondiente al punto de inflexión de la curva límite inferior, mostrada en la
fig.10.20. Para la carga última en dichos pilares, de esbeltez elevada, se puede tomar
pues la carga crítica de Euler: Ncr
Son los pilares de esbelteces medias aquellos cuyo comportamiento, tal y como se
observa en la fig.10.20, se desvía más de la teoría de Euler. Es pues en ellos donde se
observa que más influye la presencia de las imperfecciones, las cuales dan lugar a
tensiones adicionales que se añadirán a las obtenidas en el comportamiento teórico, lo
que explica que las cargas últimas que serán capaces de resistir los pilares en el pandeo
real sean inferiores a las obtenidas en el pandeo teórico.
Son la falta de rectitud del eje del pilar y la presencia de tensiones residuales, las
imperfecciones que presentan un efecto más significativo en el comportamiento de este
tipo de pilares.
Ejemplo de tensiones adicionales debidas al efecto de las tensiones residuales debidas a
la laminación en caliente en la fabricación del pilar:
0,3.fy
compresión
0,2.fy
tracción
0,2.fy
compresión
Ejemplo de tensiones residuales
debidas a laminación en caliente
+ = o
σ = N/A σResidual σmax< fy σmax= fy
16 Figura 10.21

244. Sección 10.3: Estudio práctico del pandeo: Piezas sometidas a compresión
Ejemplo de tensiones adicionales debidas a la falta de rectitud del eje del pilar:
Esta imperfección es debida a los defectos inherentes al propio material, tales como la
falta de homogeneidad del material, las imperfecciones geométricas de las piezas, etc….
La forma de introducir estas imperfecciones es a través de dar una curvatura inicial a la
barra (Fig.10.22.b). Al aplicar ahora sobre ella la carga N de compresión, hará trabajar a
la barra a FLEXIÖN-COMPRESIÖN, con lo cual se curvará más (Fig.10.22.c)
x
x x N
→ f0 →
f
y y y
Fig. 10.22.a Fig. 10.22.b Fig. 10.22.c
σ = N/A σ = (N.f).y/Iz σmax< fy σmax= fy
+ = o
Fig.10.23
Naturalmente si se dan varias imperfecciones a la vez, los efectos finales serán la suma
de los obtenidos en cada una de ellas.
17

245. Tema 10: Pandeo
Así pues en el pandeo real tendremos que, en general, a las tensiones producidas por la
carga de compresión, les tendremos que sumar las debidas a las tensiones residuales y
las debidas a la flexión, dada la falta de rectitud del eje del pilar, con lo cual la tensión
total final máxima será:
La tensión máxima se dará en la sección x = L/2 y valdrá:
x
N
N Mz N N. f
σ max = + + σ residuales = + + σ residuales =
A W A W
(σ . A). f
σ+ + σ residuales = k1.σ
W
L f
L/2 σ max = k1 .σ (10.11)
y
Fig. 10.24
N
siendo : k1 = "coeficiente de amplificación de la tensión de compresión σ = "
A
Conclusión
:
PANDEO TEÓRICO: Euler
PANDEO REAL
N
N COMPRESIÓN +FLEXIÓN+T.residuales
sólo COMPRESIÓN
N
σ max = σ ( N ) = = σ max = σ ( N ) + σ ( M z ) + σ residuales =
A
f N Mz
N + + σ residuales = k1.σ
= = σ = cte A W
A
Fig. 10.25
18

246. Sección 10.3: Estudio práctico del pandeo: Piezas sometidas a compresión
10.3.2.- INTRODUCCIÓN AL MÉTODO DE CÁLCULO A PANDEO CON LA
NUEVA NORMATIVA ESPAÑOLA: DB-SE-A (2007)
Comprobación a Pandeo de piezas sometidas a compresión centrada por el Método
de la nueva Normativa española: DB-SE-A: Caso de barras rectas de sección
constante y axil constante
La ecuación 10.11 nos da la tensión máxima en el pandeo real, en el que se tiene en
cuenta, tal y como indicamos anteriormente, las tensiones debidas a la compresión junto
con las tensiones que producen las imperfecciones del pilar (falta de rectitud del eje y
las tensiones residuales).
La fórmula propuesta por la Normativa para la comprobación a pandeo es:
N* 1
σ max = k1 .σ * = k1.
*
≤ f yd → N * ≤ . A. f yd → N * ≤ χ . A. f yd
A k1
denominando : N b , Rd = "resistencia última de la barra a pandeo" = χ . A. f yd (10.12)
1
χ= = "coeficiente de reducción por pandeo"
k1
Así pues la fórmula final para la comprobación a pandeo de una barra de sección
constante sometida a una compresión centrada constante será:
N * ≤ Nb , Rd = χ . A. f yd (10.13)
Los valores del coeficiente de reducción por pandeo χ, que como se ve, es el inverso
del coeficiente de amplificación de tensiones k1, se pueden obtener a partir de las curvas
de pandeo, como veremos a continuación
Observaciones:
1.-Al coeficiente χ<1, se le denomina “coeficiente de reducción por pandeo” por lo
siguiente:
Vimos que la resistencia última, plástica, de una sección a compresión era (ver
ecuación 4.33):
Npl,d = A.fyd
y la comprobación a resistencia de una sección trabajando a compresión se aplicaba la
fórmula dada en la ecuación (4.34)
N * ≤ N pl , d = A. f yd
Como en el caso del pandeo y tal como hemos visto, además de las tensiones debidas a
la compresión, había que añadir las debidas a la flexión y las tensiones residuales, la
resistencia última de la sección, será inferior a la de solamente debida a la compresión.
19

247. Tema 10: Pandeo
2.- Para los casos de barras de sección variable, de esfuerzos de compresión variables,
de barras de sección compuesta o de elementos triangulados o de pilares de edificios,
ver la Normativa indicada. Su estudio es objeto de otras asignaturas específicas.
10.3.3.- CURVAS EUROPEAS DE PANDEO
Las curvas de pandeo ECCS están basadas en los resultados de más de 1000 ensayos
sobre varios tipos de piezas: I, H, T, [, ∟, ⊥ , [ ], Ο, con diferentes valores de esbeltez
(entre 55 y 160). Se han tenido en cuenta una imperfección geométrica de falta de
rectitud del eje del pilar, tomando un eje semisinusoidal de magnitud f = L/1000, así
como los efectos de tensiones residuales relativas a cada tipo de sección transversal.
Las curvas de pandeo ECCS: ao, a, b, c y d, se muestran en la siguiente tabla 10.1 y el
utilizar unas u otras va a depender de la forma de la sección transversal del pilar
considerado, de la dirección en la que pueda ocurrir el pandeo (eje y o eje z) y del
proceso de fabricación utilizado en el pilar (laminación en caliente, soldado o
conformado en frío). Ver la tabla siguiente 10.2
Tabla 10.1 Curvas de pandeo
Éstas curvas nos proporcionan el valor para el coeficiente de reducción por pandeo χ,
en función de la curva de pandeo apropiada al caso y de la esbeltez reducida λ :
A. f y
λ= "esbeltez reducida" (10.14)
N cr
π 2 .E .I
siendo: N cr = (carga crítica de Euler)
L2
k
20

248. Sección 10.3: Estudio práctico del pandeo: Piezas sometidas a compresión
Tabla 10.2 Curva de pandeo en función de la sección transversal
21

249. Tema 10: Pandeo
Los datos de la tabla 10.3 que se indica a continuación, que dan también los valores del
coeficiente χ de reducción del pandeo, se obtienen de la tabla 10.1 (curvas de pandeo),
pero son más operativas a la hora de tomar datos de las mismas.
Tabla 10.3 Valores del coeficiente de pandeo χ
10.3.4.- PANDEO EN PIEZAS SOMETIDAS A FLEXIÓN-COMPRESIÓN
La Comprobación a Pandeo debido a la Flexión–Compresión se estudiará en asignaturas
específicas. (Ver normativa DB-SE-A)
22