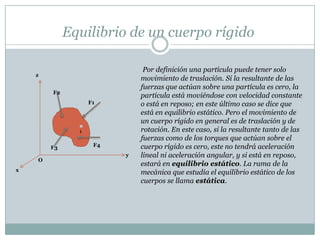
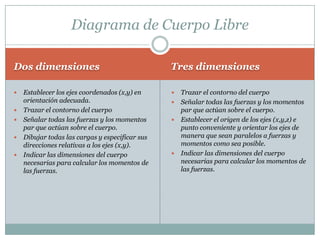
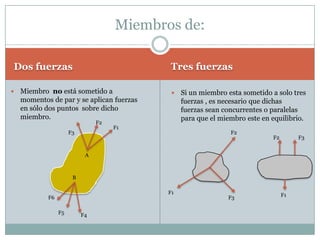
El documento habla sobre el equilibrio estático de los cuerpos rígidos. Explica que para que un cuerpo rígido esté en equilibrio, la suma de las fuerzas y de los momentos aplicados sobre él debe ser cero. También describe cómo dibujar diagramas de cuerpos libres en 2D y 3D, establecer ecuaciones de equilibrio escalares y vectoriales, y los tipos de restricciones y miembros que pueden existir en un cuerpo rígido.

1.  Stephanie Espinosa Torres
 Rosalba Torres Bailón
 Diego González Freire
 Diego Valdivieso Eguiguren

2. Equilibrio de un cuerpo rígido
Por definición una partícula puede tener solo
z
movimiento de traslación. Si la resultante de las
fuerzas que actúan sobre una partícula es cero, la
F2
partícula está moviéndose con velocidad constante
F1 o está en reposo; en este último caso se dice que
está en equilibrio estático. Pero el movimiento de
un cuerpo rígido en general es de traslación y de
i rotación. En este caso, si la resultante tanto de las
fuerzas como de los torques que actúan sobre el
F3 F4 cuerpo rígido es cero, este no tendrá aceleración
y lineal ni aceleración angular, y si está en reposo,
O
estará en equilibrio estático. La rama de la
x
mecánica que estudia el equilibrio estático de los
cuerpos se llama estática.

3. La Es la
suma de las fuerzas aplicadas al suma algebraica de los momentos
cuerpo es cero. con respecto a un punto de las
fuerzas aplicadas es igual a cero.
ΣF = 0
F1 + F2 +….+ Fn = 0 ΣM = 0
M 1 +M 2 +….+Mrn = 0

4. Diagrama de Cuerpo Libre
Dos dimensiones Tres dimensiones
 Establecer los ejes coordenados (x,y) en  Trazar el contorno del cuerpo
orientación adecuada.  Señalar todas las fuerzas y los momentos
 Trazar el contorno del cuerpo par que actúan sobre el cuerpo.
 Señalar todas las fuerzas y los momentos  Establecer el origen de los ejes (x,y,z) e
par que actúan sobre el cuerpo. punto conveniente y orientar los ejes de
 Dibujar todas las cargas y especificar sus manera que sean paralelos a fuerzas y
direcciones relativas a los ejes (x,y). momentos como sea posible.
 Indicar las dimensiones del cuerpo  Indicar las dimensiones del cuerpo
necesarias para calcular los momentos de necesarias para calcular los momentos de
las fuerzas. las fuerzas.

5. Ecuaciones de Equilibrio
Dos dimensiones Tres dimensiones
 Normalmente ecuaciones escalares de  Si las componentes (x,y,z) de fuerza y
equilibrio: ΣFx = 0, ΣFy = 0, ΣM O = 0 momento parecen fáciles de determinar,
entonces se usa las ecuaciones
 Sumar fuerzas a lo largo de un eje de
vectoriales.
manera que elimine tantas fuerzas
 Elegir la dirección de un eje para la suma
desconocidas como sea posible.
de los momentos de tal manera q
 Sume momentos con respecto a un punto
interseque la línea de acción de esta
O que pase por la línea acción de tantas forma los momentos y fuerzas que sean
fuerzas desconocidas como sea posible. paralelas a este eje seran igual a cero.ç
 Si la solucion resulta un escalar negativo
para la magnitud de la fuerza o momento
par; eso indica que el signo es contrario
al supuesto en el diagrama

6. Miembros de:
Dos fuerzas Tres fuerzas
 Miembro no está sometido a  Si un miembro esta sometido a solo tres
momentos de par y se aplican fuerzas fuerzas , es necesario que dichas
en sólo dos puntos sobre dicho fuerzas sean concurrentes o paralelas
miembro. para que el miembro este en equilibrio.
F2
F1
F3 F2
F2 F3
A
B
F1 F1
F6 F3
F5 F4

7. Restricciones para un cuerpo rígido
Restricciones
Restricciones Impropias
Redundantes
 Cuando tiene soportes  En algunos casos puede haber
redundantes, es decir mas de los tantas fuerzas desconocidas sobre
necesarios para mantenerlo en el cuerpo como ecuaciones de
equilibrio se vuelve estáticamente equilibrio; sin embargo puede
indeterminado (más cargas mostrar inestabilidad debido a las
desconocidas). restricciones impropias de los
soportes

8. Bibliografia
• H I B B E L E R . R U S S E L , “ E S TÁT I C A” D E C I M A
E D I C I Ó N , P E A R S O N E D U C AT I O N , 2 0 0 4 .
•H T T P : / / W W W 2 . U D E C . C L / ~ J I N Z U N Z A
/FISICA/CAP6.PDF

9. GRACIAS